华师版数学八年级上册 13.3等腰三角形第1课时 等腰三角形的性质课件(共21张PPT)
文档属性
| 名称 | 华师版数学八年级上册 13.3等腰三角形第1课时 等腰三角形的性质课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 626.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-13 19:08:51 | ||
图片预览






文档简介
(共21张PPT)
13.3 等腰三角形
第1课时 等腰三角形的性质
学习目标
了解等腰三角形的概念,探索并证明等腰三角形的性质定理:底边上的高线、中线及顶角平分线重合;
探索等边三角形的性质定理:等边三角形的各角都等于60°.
我们在小学的时候曾经学过三角形的分类,按边分三角形可以怎样分类?什么叫等腰三角形?
等腰三角形
三条边都相等的等边三角形
(也叫正三角形)
三条边都不相等
三角形
不等边三角形
底边和腰不相等的等腰三角形
有两条边相等的三角形叫做等腰三角形.
新知讲解
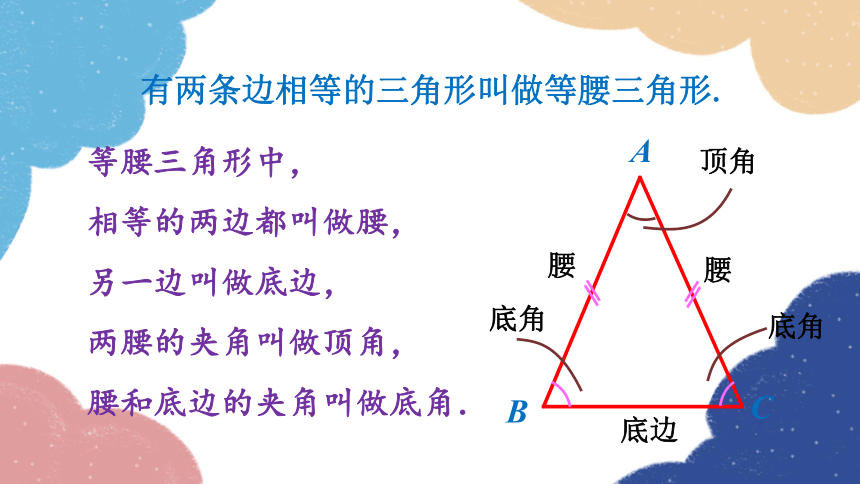
有两条边相等的三角形叫做等腰三角形.
腰
腰
底边
顶角
底角
A
B
C
底角
等腰三角形中,
相等的两边都叫做腰,
另一边叫做底边,
两腰的夹角叫做顶角,
腰和底边的夹角叫做底角.
做一做
剪一张等腰三角形的半透明纸片,每人所剪的等腰三角形的大小和形状可以不一样,如图,把纸片对折,让两腰AB、AC重叠在一起,折痕为AD.你有什么发现?
△ABC为轴对称图形,
对称轴为AD,
∠B=∠C.
A
B
C
D
A
B
C
D
等腰三角形的性质1
性质:
等腰三角形的两底角相等(简写成“等边对等角”).
注意:(1)适用条件:必须在同一个三角形中.
(2) 作用:它是证明角相等常用的方法, 它的
应用可省去三角形全等的证明, 因而更简便.
你会证明这个性质吗?
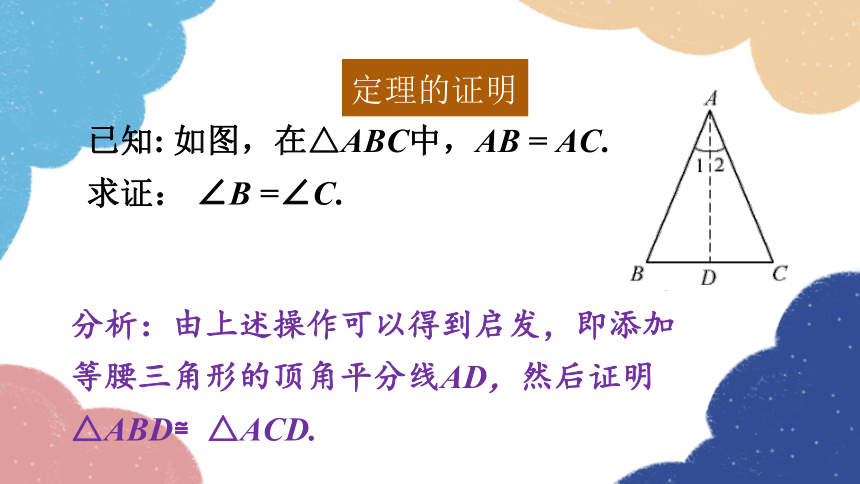
已知: 如图,在△ABC中,AB = AC.
求证: ∠B =∠C.
分析:由上述操作可以得到启发,即添加等腰三角形的顶角平分线AD,然后证明△ABD≌△ACD.
定理的证明
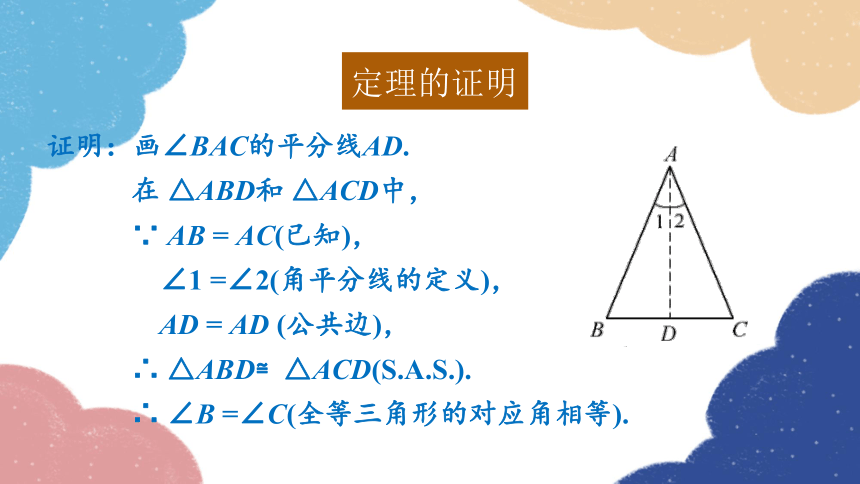
证明:画∠BAC的平分线AD.
在 △ABD和 △ACD中,
∵ AB = AC(已知),
∠1 =∠2(角平分线的定义),
AD = AD (公共边),
∴ △ABD≌△ACD(S.A.S.).
∴ ∠B =∠C(全等三角形的对应角相等).
定理的证明
例题
【例1】已知:在△ABC中, AB = AC , ∠B = 80°.求 ∠C和∠A的大小.
解:∵ AB = AC (已知),
∴ ∠C =∠B = 80°(等边对等角).
又∵ ∠A +∠B +∠C = 180°(三角形的内角和等于 180°),
∴ ∠A = 180 °-∠B -∠C (等式的性质)
= 180°- 80°- 80°= 20°.
探索
重合的线段 重合的角
A
B
D
C
AB = AC
BD = CD
AD = AD
∠B =∠C
∠BAD =∠CAD
∠ADB =∠ADC
= 90°
在刚刚的“做一做”中,你还能发现什么?
等腰三角形的性质2
等腰三角形底边上的高、中线及顶角的平分线互相重合 (简称“三线合一”).
应用:证明线段相等、角相等、垂直等关系的重要方法.
【例2】如图 ,在△ABC中, AB = AC ,D是BC 边上的中点, ∠B = 30°.求:
(1)∠ADC的大小;(2)∠1的大小.
例题
解:(1)∵ AB = AC,BD = DC (已知),
∴AD⊥BC (等腰三角形的“三线合一”),
∴∠ADC =∠ADB = 90°.
(2)∵∠1+∠B +∠ADB = 180°
(三角形的内角和等于 180 °),
∠B = 30 °(已知),
∴∠1 = 180 °-∠B -∠ ADB (等式的性质)
= 180°- 30°- 90°= 60°.
【例2】如图 ,在△ABC中, AB = AC ,D是BC 边上的中点, ∠B = 30°.求:
(1)∠ADC的大小;(2)∠1的大小.
探究
等腰三角形底角的范围是什么?顶角呢?
由等腰三角形性质1和三角形内角和等于180°可知,底角的2倍小于180°,故底角的范围为0°~90°;
顶角的范围为0°~180°.(不含两端值)
当顶角为60°时,底角等于多少度?
新知
三条边都相等的三角形是等边三角形.
A
C
B
当顶角等于60°时,底角也为60°.
猜测:三条边有什么关系?
等边三角形有什么性质?
等边三角形的性质
等边三角形的各个角都相等,并且每一个角都等于60°.
等边三角形的三条边都相等,三个角都相等,也称为正三角形.
思考
由前面的做一做可知,等腰三角形是轴对称图形,那么,等边三角形是轴对称图形吗?如果是,对称轴有几条?等边三角形和等腰三角形有什么关系?
提示:等边三角形是轴对称图形,对称轴有3条,等边三角形是特殊的等腰三角形.
课后小组沟通交流.
练习
1.如图,在△ABC中,AB = AC,点D,E在BC上,连接AD,AE,如果只添加一个条件使
∠DAB =∠EAC,则添加的条件不能为( )
A.BD = CE B.AD = AE
C.DA = DE D.BE = CD
C
2.如图,在△ABC中,AB = AC,AD⊥BC于点D,DE⊥AB于点E,DF⊥AC于点F,下列结论:①∠BAD = ∠CAD;②BD = CD;③若点P在直线AD上,则PB = PC ;
④ DE = DF.
其中正确的是___________.
①②③④
3.如图,在△ABC中,AB = AC,AD是BC边上的中线.若∠BAD = 25°,求∠C的度数.
等腰三角形的性质
等边对等角
等边三角形
同一个三角形中
顶角的平分线、底边上的高和中线才有这一性质.而腰上高、中线和底角的平分线不具有这一性质.
三线合一
三条边都相等,每个内角等于60°.
小结
13.3 等腰三角形
第1课时 等腰三角形的性质
学习目标
了解等腰三角形的概念,探索并证明等腰三角形的性质定理:底边上的高线、中线及顶角平分线重合;
探索等边三角形的性质定理:等边三角形的各角都等于60°.
我们在小学的时候曾经学过三角形的分类,按边分三角形可以怎样分类?什么叫等腰三角形?
等腰三角形
三条边都相等的等边三角形
(也叫正三角形)
三条边都不相等
三角形
不等边三角形
底边和腰不相等的等腰三角形
有两条边相等的三角形叫做等腰三角形.
新知讲解
有两条边相等的三角形叫做等腰三角形.
腰
腰
底边
顶角
底角
A
B
C
底角
等腰三角形中,
相等的两边都叫做腰,
另一边叫做底边,
两腰的夹角叫做顶角,
腰和底边的夹角叫做底角.
做一做
剪一张等腰三角形的半透明纸片,每人所剪的等腰三角形的大小和形状可以不一样,如图,把纸片对折,让两腰AB、AC重叠在一起,折痕为AD.你有什么发现?
△ABC为轴对称图形,
对称轴为AD,
∠B=∠C.
A
B
C
D
A
B
C
D
等腰三角形的性质1
性质:
等腰三角形的两底角相等(简写成“等边对等角”).
注意:(1)适用条件:必须在同一个三角形中.
(2) 作用:它是证明角相等常用的方法, 它的
应用可省去三角形全等的证明, 因而更简便.
你会证明这个性质吗?
已知: 如图,在△ABC中,AB = AC.
求证: ∠B =∠C.
分析:由上述操作可以得到启发,即添加等腰三角形的顶角平分线AD,然后证明△ABD≌△ACD.
定理的证明
证明:画∠BAC的平分线AD.
在 △ABD和 △ACD中,
∵ AB = AC(已知),
∠1 =∠2(角平分线的定义),
AD = AD (公共边),
∴ △ABD≌△ACD(S.A.S.).
∴ ∠B =∠C(全等三角形的对应角相等).
定理的证明
例题
【例1】已知:在△ABC中, AB = AC , ∠B = 80°.求 ∠C和∠A的大小.
解:∵ AB = AC (已知),
∴ ∠C =∠B = 80°(等边对等角).
又∵ ∠A +∠B +∠C = 180°(三角形的内角和等于 180°),
∴ ∠A = 180 °-∠B -∠C (等式的性质)
= 180°- 80°- 80°= 20°.
探索
重合的线段 重合的角
A
B
D
C
AB = AC
BD = CD
AD = AD
∠B =∠C
∠BAD =∠CAD
∠ADB =∠ADC
= 90°
在刚刚的“做一做”中,你还能发现什么?
等腰三角形的性质2
等腰三角形底边上的高、中线及顶角的平分线互相重合 (简称“三线合一”).
应用:证明线段相等、角相等、垂直等关系的重要方法.
【例2】如图 ,在△ABC中, AB = AC ,D是BC 边上的中点, ∠B = 30°.求:
(1)∠ADC的大小;(2)∠1的大小.
例题
解:(1)∵ AB = AC,BD = DC (已知),
∴AD⊥BC (等腰三角形的“三线合一”),
∴∠ADC =∠ADB = 90°.
(2)∵∠1+∠B +∠ADB = 180°
(三角形的内角和等于 180 °),
∠B = 30 °(已知),
∴∠1 = 180 °-∠B -∠ ADB (等式的性质)
= 180°- 30°- 90°= 60°.
【例2】如图 ,在△ABC中, AB = AC ,D是BC 边上的中点, ∠B = 30°.求:
(1)∠ADC的大小;(2)∠1的大小.
探究
等腰三角形底角的范围是什么?顶角呢?
由等腰三角形性质1和三角形内角和等于180°可知,底角的2倍小于180°,故底角的范围为0°~90°;
顶角的范围为0°~180°.(不含两端值)
当顶角为60°时,底角等于多少度?
新知
三条边都相等的三角形是等边三角形.
A
C
B
当顶角等于60°时,底角也为60°.
猜测:三条边有什么关系?
等边三角形有什么性质?
等边三角形的性质
等边三角形的各个角都相等,并且每一个角都等于60°.
等边三角形的三条边都相等,三个角都相等,也称为正三角形.
思考
由前面的做一做可知,等腰三角形是轴对称图形,那么,等边三角形是轴对称图形吗?如果是,对称轴有几条?等边三角形和等腰三角形有什么关系?
提示:等边三角形是轴对称图形,对称轴有3条,等边三角形是特殊的等腰三角形.
课后小组沟通交流.
练习
1.如图,在△ABC中,AB = AC,点D,E在BC上,连接AD,AE,如果只添加一个条件使
∠DAB =∠EAC,则添加的条件不能为( )
A.BD = CE B.AD = AE
C.DA = DE D.BE = CD
C
2.如图,在△ABC中,AB = AC,AD⊥BC于点D,DE⊥AB于点E,DF⊥AC于点F,下列结论:①∠BAD = ∠CAD;②BD = CD;③若点P在直线AD上,则PB = PC ;
④ DE = DF.
其中正确的是___________.
①②③④
3.如图,在△ABC中,AB = AC,AD是BC边上的中线.若∠BAD = 25°,求∠C的度数.
等腰三角形的性质
等边对等角
等边三角形
同一个三角形中
顶角的平分线、底边上的高和中线才有这一性质.而腰上高、中线和底角的平分线不具有这一性质.
三线合一
三条边都相等,每个内角等于60°.
小结
