青岛版数学八年级上册 2.5 角平分线的性质 课件(共17张PPT)
文档属性
| 名称 | 青岛版数学八年级上册 2.5 角平分线的性质 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 635.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-13 00:00:00 | ||
图片预览




文档简介
(共17张PPT)
第2章 图形的轴对称
2.5 角平分线的性质
学习目标
1.通过折纸、画图等操作,体会角的轴对称性,理解角的平分线所在的直线是它的对称轴.
2.掌握角平分线的性质和判定,能够利用它们解决一些实际问题.
3.会用尺规作图作一个角的平分线,并能写出具体的作图步骤.
4.经历探索角平分线的性质的过程,进一步培养推理的意识和能力,熟悉几何推理的基本思想.
B
活动探究
试一试:在纸上任意画一个∠BAC,把它沿经过点A的某条直线对折,使角的两边BA与AC重合然后把纸展开后铺平,折痕记为AD,你发现什么现象?
由此,我们可以得到如下结论:
角是 图形,
它的对称轴是 .
C
B
A
D
轴对称
AD
角的平分线所在的直线是它的对称轴.
C
B
A
D
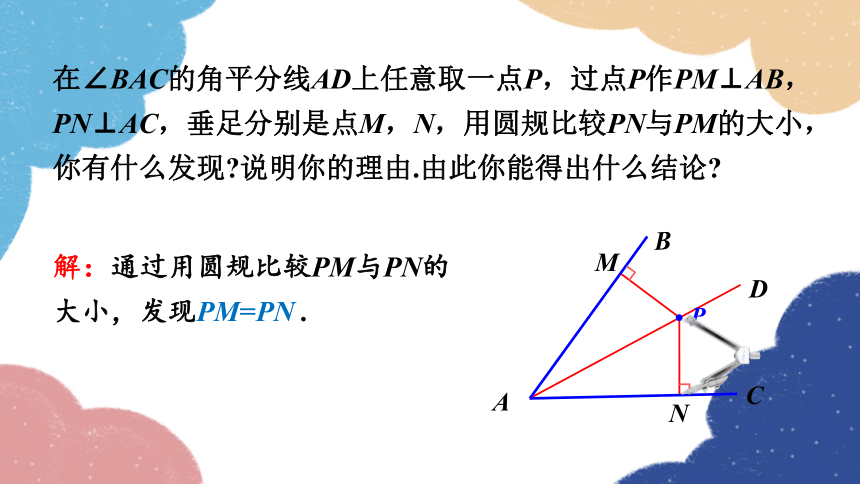
在∠BAC的角平分线AD上任意取一点P,过点P作PM⊥AB,PN⊥AC,垂足分别是点M,N,用圆规比较PN与PM的大小,你有什么发现 说明你的理由.由此你能得出什么结论
P
M
N
解:通过用圆规比较PM与PN的大小,发现PM=PN .
解:因为AD平分∠BAC,所以 ∠1= ∠2
因为PM⊥AB,PN⊥AC,
所以 ∠ AMP=∠ANP=90°.
在△AMP与△ANP中,
因为
所以△AMP ≌ △ANP(AAS).
所以PM=PN.
∠1=∠2,
∠ AMP=∠ANP,
AP=AP,
C
B
A
D
P
M
N
1
2
角平分线上的点,到这个角的两边的距离相等.
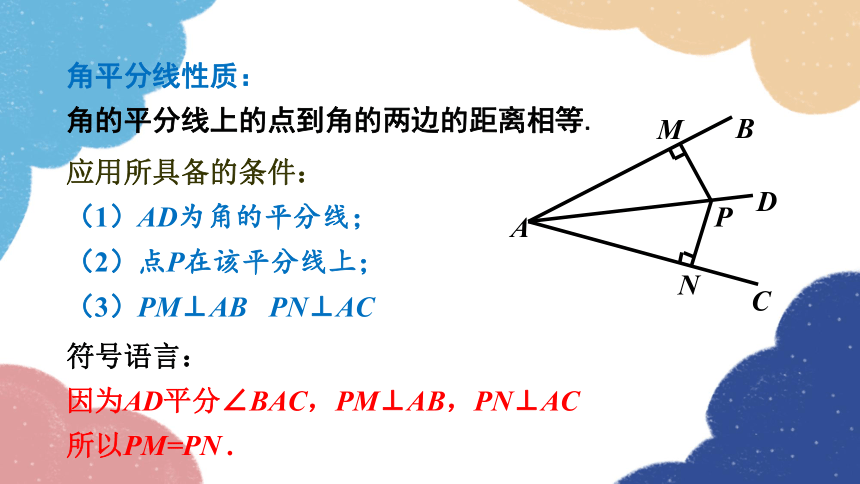
角平分线性质:
角的平分线上的点到角的两边的距离相等.
C
B
M
A
P
N
D
应用所具备的条件:
(1)AD为角的平分线;
(2)点P在该平分线上;
(3)PM⊥AB PN⊥AC
符号语言:
因为AD平分∠BAC,PM⊥AB,PN⊥AC
所以PM=PN .
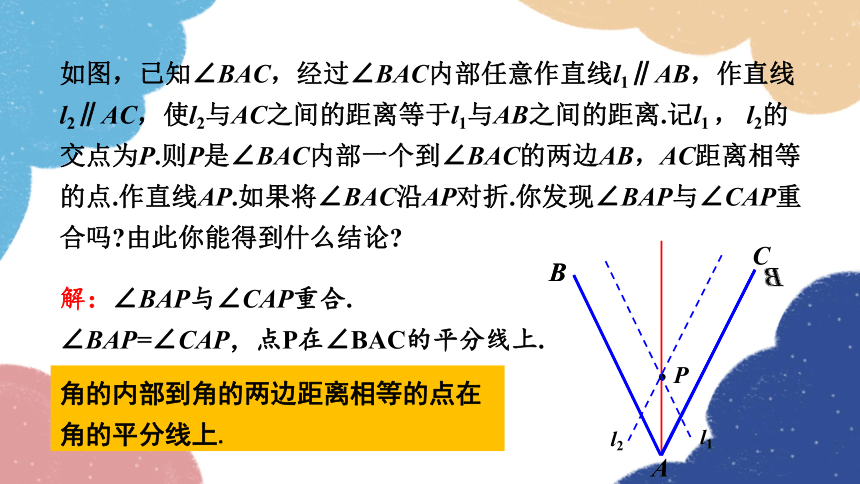
如图,已知∠BAC,经过∠BAC内部任意作直线l1∥AB,作直线l2∥AC,使l2与AC之间的距离等于l1与AB之间的距离.记l1 , l2的交点为P.则P是∠BAC内部一个到∠BAC的两边AB,AC距离相等的点.作直线AP.如果将∠BAC沿AP对折.你发现∠BAP与∠CAP重合吗 由此你能得到什么结论
B
C
B
A
P
解:∠BAP与∠CAP重合.
∠BAP=∠CAP,点P在∠BAC的平分线上.
角的内部到角的两边距离相等的点在角的平分线上.
l1
l2
角平分线的判定:
角的内部到角的两边距离相等的点在角的平分线上.
应用所具备的条件:
(1)点P在∠BAC的内部;
(2)PM⊥AB PN⊥AC;
(3)PM=PN.
符号语言:
因为 PM⊥AB,PN⊥AC,PM=PN;
所以点P在∠BAC的角平分线上,所以∠1=∠2.
C
B
A
D
P
M
N
1
2
已知:∠BAC .
求作:∠BAC 的平分线.
A
B
C
E
F
P
已知一个角,你能用直尺和圆规作出它的平分线吗?
你能说明所作出的射线AP是∠BAC的平分线吗?
A
B
C
E
F
P
连接PE,PF,
因为AE=AF,EP=FP,
由SSS,△APE≌△APF.
所以∠BAP=∠CAP.
【例】如图,△ABC的角平分线BM,CN相交于点P.
试说明:点P到三边AB、BC、CA的距离相等.
因为BM是△ABC的角平分线,
点P在BM上,
所以PD=PE.
同理,PE=PF.
所以PD=PE=PF.
即点P到三边AB、BC、CA的距离相等.
解:过点P作PD⊥AB于D,
PE⊥BC于E,PF⊥AC于F,
D
P
M
N
A
B
C
F
E
D
P
M
N
A
B
C
F
E
结论:三角形的三条角平分线交于一点,
并且这点到三边的距离相等.
想一想,点P在∠A的平分线上吗?
这说明三角形的三条角平分线有什么关系?
1.如图所示,Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于点D,若CD=3 cm,则点D到AB的距离DE长度是( )
A.5 cm B.4 cm C.3 cm D.2 cm
C
随堂练习
解:作夹角的角平分线OC,
截取OD=2.5cm ,D即为所求.
D
2.如图,要在S区建一个贸易市场,使它到铁路和公路距离相等, 离公路与铁路交叉处500米,这个贸易市场应建在何处?(比例尺为1︰20000)
O
C
200
400m
0
比例尺:
3.如图,已知△ABC的外角∠CBD和∠BCE的平分线相交于点F,
求证:点F在∠DAE的平分线上.
A
B
D
C
E
F
G
H
M
A
B
D
C
E
F
证明:过点F作FG⊥AE于G,FH⊥AD于H,
FM⊥BC于M.
因为点F在∠BCE的平分线上,
FG⊥AE, FM⊥BC,
所以FG=FM.
又因为点F在∠CBD平分线上,
FH⊥AD, FM⊥BC.
所以FM=FH.
所以FG=FH,
所以点F在∠DAE的平分线上.
角平分线
性质
判定
角平分线上的点到
角两边的距离相等.
到角的两边距离相等
的点在角平分线上.
因为 QD⊥OA,QE⊥OB,
点Q在∠AOB的平分线上,
所以 QD=QE.
因为 QD⊥OA,QE⊥OB,
QD=QE.
所以点Q在∠AOB平分线上.
应用
课堂小结
第2章 图形的轴对称
2.5 角平分线的性质
学习目标
1.通过折纸、画图等操作,体会角的轴对称性,理解角的平分线所在的直线是它的对称轴.
2.掌握角平分线的性质和判定,能够利用它们解决一些实际问题.
3.会用尺规作图作一个角的平分线,并能写出具体的作图步骤.
4.经历探索角平分线的性质的过程,进一步培养推理的意识和能力,熟悉几何推理的基本思想.
B
活动探究
试一试:在纸上任意画一个∠BAC,把它沿经过点A的某条直线对折,使角的两边BA与AC重合然后把纸展开后铺平,折痕记为AD,你发现什么现象?
由此,我们可以得到如下结论:
角是 图形,
它的对称轴是 .
C
B
A
D
轴对称
AD
角的平分线所在的直线是它的对称轴.
C
B
A
D
在∠BAC的角平分线AD上任意取一点P,过点P作PM⊥AB,PN⊥AC,垂足分别是点M,N,用圆规比较PN与PM的大小,你有什么发现 说明你的理由.由此你能得出什么结论
P
M
N
解:通过用圆规比较PM与PN的大小,发现PM=PN .
解:因为AD平分∠BAC,所以 ∠1= ∠2
因为PM⊥AB,PN⊥AC,
所以 ∠ AMP=∠ANP=90°.
在△AMP与△ANP中,
因为
所以△AMP ≌ △ANP(AAS).
所以PM=PN.
∠1=∠2,
∠ AMP=∠ANP,
AP=AP,
C
B
A
D
P
M
N
1
2
角平分线上的点,到这个角的两边的距离相等.
角平分线性质:
角的平分线上的点到角的两边的距离相等.
C
B
M
A
P
N
D
应用所具备的条件:
(1)AD为角的平分线;
(2)点P在该平分线上;
(3)PM⊥AB PN⊥AC
符号语言:
因为AD平分∠BAC,PM⊥AB,PN⊥AC
所以PM=PN .
如图,已知∠BAC,经过∠BAC内部任意作直线l1∥AB,作直线l2∥AC,使l2与AC之间的距离等于l1与AB之间的距离.记l1 , l2的交点为P.则P是∠BAC内部一个到∠BAC的两边AB,AC距离相等的点.作直线AP.如果将∠BAC沿AP对折.你发现∠BAP与∠CAP重合吗 由此你能得到什么结论
B
C
B
A
P
解:∠BAP与∠CAP重合.
∠BAP=∠CAP,点P在∠BAC的平分线上.
角的内部到角的两边距离相等的点在角的平分线上.
l1
l2
角平分线的判定:
角的内部到角的两边距离相等的点在角的平分线上.
应用所具备的条件:
(1)点P在∠BAC的内部;
(2)PM⊥AB PN⊥AC;
(3)PM=PN.
符号语言:
因为 PM⊥AB,PN⊥AC,PM=PN;
所以点P在∠BAC的角平分线上,所以∠1=∠2.
C
B
A
D
P
M
N
1
2
已知:∠BAC .
求作:∠BAC 的平分线.
A
B
C
E
F
P
已知一个角,你能用直尺和圆规作出它的平分线吗?
你能说明所作出的射线AP是∠BAC的平分线吗?
A
B
C
E
F
P
连接PE,PF,
因为AE=AF,EP=FP,
由SSS,△APE≌△APF.
所以∠BAP=∠CAP.
【例】如图,△ABC的角平分线BM,CN相交于点P.
试说明:点P到三边AB、BC、CA的距离相等.
因为BM是△ABC的角平分线,
点P在BM上,
所以PD=PE.
同理,PE=PF.
所以PD=PE=PF.
即点P到三边AB、BC、CA的距离相等.
解:过点P作PD⊥AB于D,
PE⊥BC于E,PF⊥AC于F,
D
P
M
N
A
B
C
F
E
D
P
M
N
A
B
C
F
E
结论:三角形的三条角平分线交于一点,
并且这点到三边的距离相等.
想一想,点P在∠A的平分线上吗?
这说明三角形的三条角平分线有什么关系?
1.如图所示,Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于点D,若CD=3 cm,则点D到AB的距离DE长度是( )
A.5 cm B.4 cm C.3 cm D.2 cm
C
随堂练习
解:作夹角的角平分线OC,
截取OD=2.5cm ,D即为所求.
D
2.如图,要在S区建一个贸易市场,使它到铁路和公路距离相等, 离公路与铁路交叉处500米,这个贸易市场应建在何处?(比例尺为1︰20000)
O
C
200
400m
0
比例尺:
3.如图,已知△ABC的外角∠CBD和∠BCE的平分线相交于点F,
求证:点F在∠DAE的平分线上.
A
B
D
C
E
F
G
H
M
A
B
D
C
E
F
证明:过点F作FG⊥AE于G,FH⊥AD于H,
FM⊥BC于M.
因为点F在∠BCE的平分线上,
FG⊥AE, FM⊥BC,
所以FG=FM.
又因为点F在∠CBD平分线上,
FH⊥AD, FM⊥BC.
所以FM=FH.
所以FG=FH,
所以点F在∠DAE的平分线上.
角平分线
性质
判定
角平分线上的点到
角两边的距离相等.
到角的两边距离相等
的点在角平分线上.
因为 QD⊥OA,QE⊥OB,
点Q在∠AOB的平分线上,
所以 QD=QE.
因为 QD⊥OA,QE⊥OB,
QD=QE.
所以点Q在∠AOB平分线上.
应用
课堂小结
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
