函数的奇偶性
图片预览







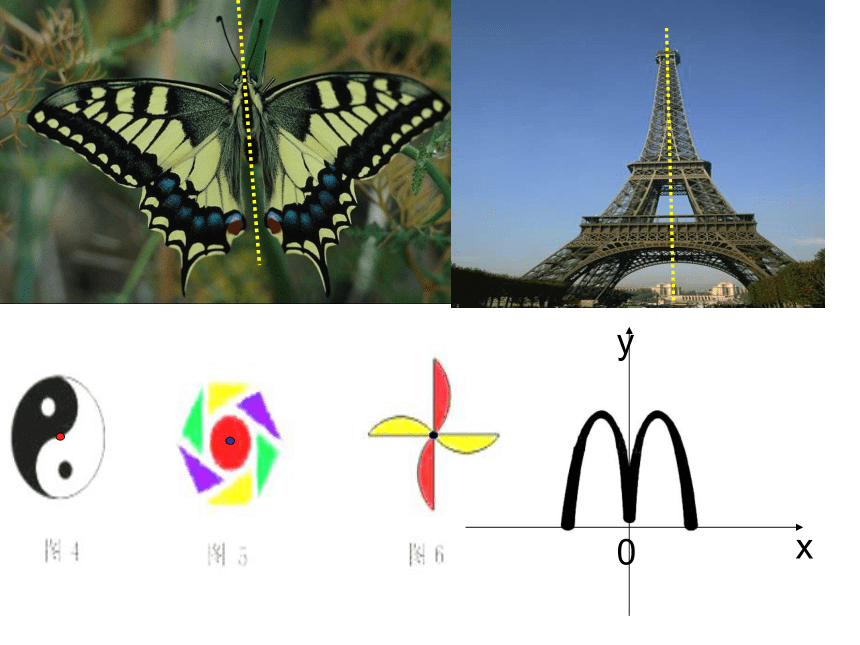
文档简介
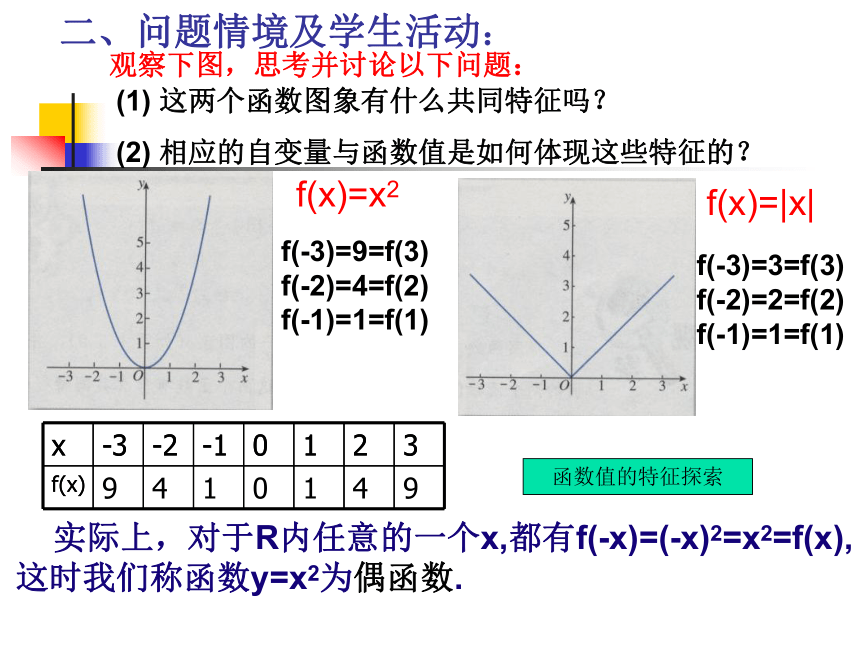
课件21张PPT。1.3.2函数的奇偶性 泽国中学数学组 观察下列图片,你有何感受?一、引入观察下图,思考并讨论以下问题:(1) 这两个函数图象有什么共同特征吗?
(2) 相应的自变量与函数值是如何体现这些特征的?f(-3)=9=f(3) f(-2)=4=f(2) f(-1)=1=f(1)f(-3)=3=f(3) f(-2)=2=f(2) f(-1)=1=f(1) 实际上,对于R内任意的一个x,都有f(-x)=(-x)2=x2=f(x),这时我们称函数y=x2为偶函数.二、问题情境及学生活动:函数值的特征探索1.偶函数 一般地,对于函数f(x)的定义域内的任意一个x,
都有f(-x)=f(x),那么f(x)就叫做偶函数. 例如,函数 都是偶函数,它们的图象分别如下图(1)、(2)所示.三、建构数学: 观察函数f(x)=x和f(x)=1/x的图象(下图),你能发现两个函数图象有什么共同特征吗?f(-3)=-3=-f(3) f(-2)=-2=-f(2) f(-1)=-1=-f(1) 实际上,对于R内任意的一个x,都有f(-x)=-x=-f(x),这时我们称函数y=x为奇函数.f(-3)=-1/3=-f(3) f(-2)=-1/2=-f(2) f(-1)=-1=-f(1)函数值特征探索2.奇函数 一般地,对于函数f(x)的定义域内的任意一个x,都有f(-x)= - f(x),那么f(x)就叫做奇函数. 定义域关于原点对称三、建构数学:探究1:
有奇偶性的函数,其定义域具有怎样的特点?
函数f(x)=x2,x [-3,2]具有奇偶性吗?为什么?
如果函数y=f(x)是奇函数或偶函数,我们就说函数y=f(x)具有奇偶性。例、判断下列函数的奇偶性:(1)解:定义域为R ∵ f(-x)=(-x)4=f(x)即f(-x)=f(x)∴f(x)偶函数(2)解:定义域为R ∵ f(-x)=(-x)5=-x=-f(x)即f(-x)=-f(x)∴f(x)奇函数(3)解:定义域为{x|x≠0} ∵ f(-x)=-x+1/(-x)=-f(x)即f(-x)=-f(x)∴f(x)奇函数(4)解:定义域为{x|x≠0} ∵ f(-x)=1/(-x)2=f(x)即f(-x)=f(x)∴f(x)偶函数四、数学运用:3.用定义判断函数奇偶性的步骤:(1)、先求定义域,看是否关于原点对称;(2)、再判断f(-x)=-f(x)或f(-x)=f(x)是否恒成立.(3)、结论.课堂练习判断下列函数的奇偶性:探究2:
猜想:有没有既是奇函数,又是偶函数的函数?
有没有既不是奇函数,又不是偶函数的函数? 例2、已知函数y=f(x)是偶函数,它在y轴右边的图象如下图,画出在y轴左边的图象.解:画法略练习:书本P39:思考(1)已知函数y=f(x)是
上的奇函数,它在 上的图像如图所示,画出它在 上的图像。练习:(2)求函数y=f(x)在 上的函数
解析式,在 上呢?延伸探究:(3)设f(x)是定义在R上的奇函数,当x>0时,f(x)=2x+1,求x<0时,f(x)的解析式,
变:设f(x)是定义在R上的奇函数,当x>0时,f(x)=2x+1,求f(x)的解析式,1、两个定义:对于f(x)定义域内的任意一个x,
如果都有f(-x)=-f(x) f(x)为奇函数
如果都有f(-x)=f(x) f(x)为偶函数五、回顾小结:2、两个性质:
一个函数为奇函数 它的图象关于原点对称
一个函数为偶函数 它的图象关于y轴对称六、作业:(1)课本P43 A组:6;B组:3。
(2)作业本A “函数奇偶性”
谢 谢 大 家!
(2) 相应的自变量与函数值是如何体现这些特征的?f(-3)=9=f(3) f(-2)=4=f(2) f(-1)=1=f(1)f(-3)=3=f(3) f(-2)=2=f(2) f(-1)=1=f(1) 实际上,对于R内任意的一个x,都有f(-x)=(-x)2=x2=f(x),这时我们称函数y=x2为偶函数.二、问题情境及学生活动:函数值的特征探索1.偶函数 一般地,对于函数f(x)的定义域内的任意一个x,
都有f(-x)=f(x),那么f(x)就叫做偶函数. 例如,函数 都是偶函数,它们的图象分别如下图(1)、(2)所示.三、建构数学: 观察函数f(x)=x和f(x)=1/x的图象(下图),你能发现两个函数图象有什么共同特征吗?f(-3)=-3=-f(3) f(-2)=-2=-f(2) f(-1)=-1=-f(1) 实际上,对于R内任意的一个x,都有f(-x)=-x=-f(x),这时我们称函数y=x为奇函数.f(-3)=-1/3=-f(3) f(-2)=-1/2=-f(2) f(-1)=-1=-f(1)函数值特征探索2.奇函数 一般地,对于函数f(x)的定义域内的任意一个x,都有f(-x)= - f(x),那么f(x)就叫做奇函数. 定义域关于原点对称三、建构数学:探究1:
有奇偶性的函数,其定义域具有怎样的特点?
函数f(x)=x2,x [-3,2]具有奇偶性吗?为什么?
如果函数y=f(x)是奇函数或偶函数,我们就说函数y=f(x)具有奇偶性。例、判断下列函数的奇偶性:(1)解:定义域为R ∵ f(-x)=(-x)4=f(x)即f(-x)=f(x)∴f(x)偶函数(2)解:定义域为R ∵ f(-x)=(-x)5=-x=-f(x)即f(-x)=-f(x)∴f(x)奇函数(3)解:定义域为{x|x≠0} ∵ f(-x)=-x+1/(-x)=-f(x)即f(-x)=-f(x)∴f(x)奇函数(4)解:定义域为{x|x≠0} ∵ f(-x)=1/(-x)2=f(x)即f(-x)=f(x)∴f(x)偶函数四、数学运用:3.用定义判断函数奇偶性的步骤:(1)、先求定义域,看是否关于原点对称;(2)、再判断f(-x)=-f(x)或f(-x)=f(x)是否恒成立.(3)、结论.课堂练习判断下列函数的奇偶性:探究2:
猜想:有没有既是奇函数,又是偶函数的函数?
有没有既不是奇函数,又不是偶函数的函数? 例2、已知函数y=f(x)是偶函数,它在y轴右边的图象如下图,画出在y轴左边的图象.解:画法略练习:书本P39:思考(1)已知函数y=f(x)是
上的奇函数,它在 上的图像如图所示,画出它在 上的图像。练习:(2)求函数y=f(x)在 上的函数
解析式,在 上呢?延伸探究:(3)设f(x)是定义在R上的奇函数,当x>0时,f(x)=2x+1,求x<0时,f(x)的解析式,
变:设f(x)是定义在R上的奇函数,当x>0时,f(x)=2x+1,求f(x)的解析式,1、两个定义:对于f(x)定义域内的任意一个x,
如果都有f(-x)=-f(x) f(x)为奇函数
如果都有f(-x)=f(x) f(x)为偶函数五、回顾小结:2、两个性质:
一个函数为奇函数 它的图象关于原点对称
一个函数为偶函数 它的图象关于y轴对称六、作业:(1)课本P43 A组:6;B组:3。
(2)作业本A “函数奇偶性”
谢 谢 大 家!
