21.3实际问题与一元二次方程(3)——几何问题 课件(37张PPT)
文档属性
| 名称 | 21.3实际问题与一元二次方程(3)——几何问题 课件(37张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-14 13:37:15 | ||
图片预览





文档简介
(共37张PPT)
21.3实际问题与一元二次方程(3)
——几何问题
人教版九年级上册
教学目标
1.能正确利用一元二次方程的相关知识解决几何图形的面积问题.
2.经历将实际的几何问题转化为数学问题的过程,进一步深入体会一元二次方程在实际生活中的应用,提高数学应用意识.
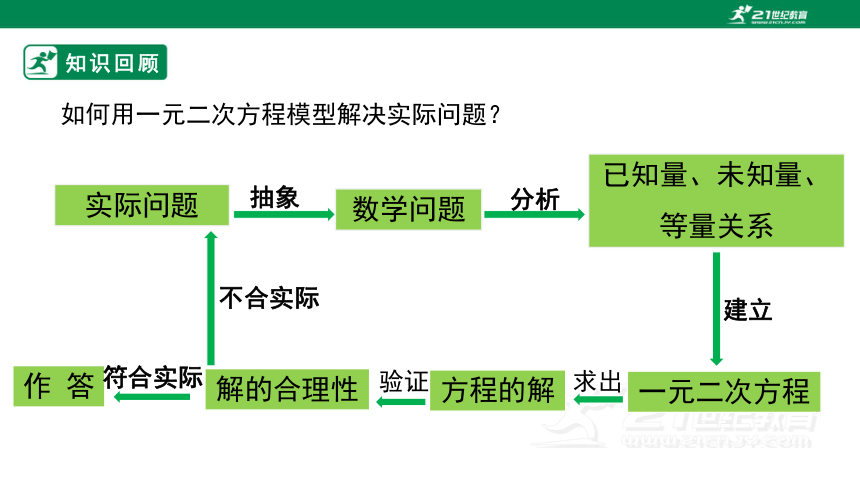
知识回顾
实际问题
已知量、未知量、
等量关系
数学问题
一元二次方程
解的合理性
方程的解
作 答
求出
验证
符合实际
不合实际
建立
抽象
分析
如何用一元二次方程模型解决实际问题?
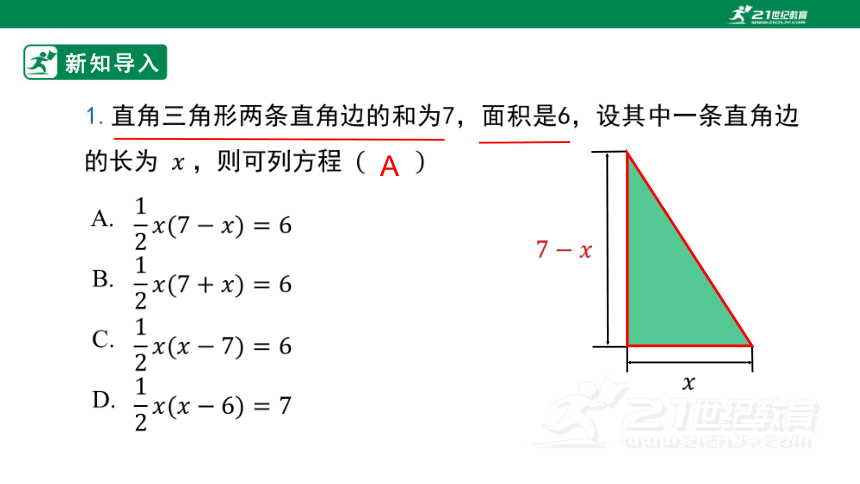
新知导入
A
新知探究
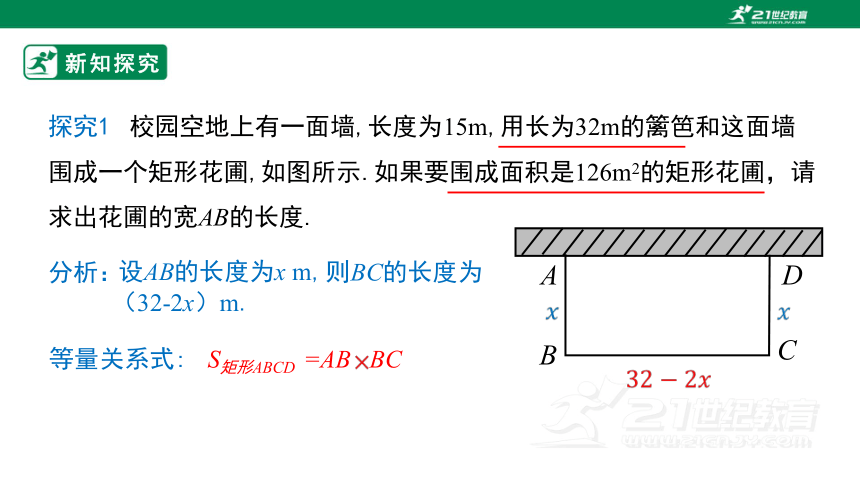
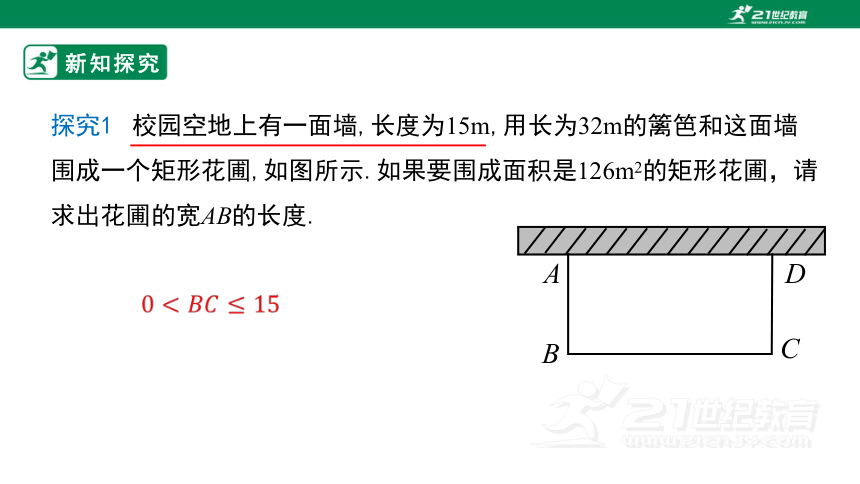
探究1 校园空地上有一面墙,长度为15m,用长为32m的篱笆和这面墙围成一个矩形花圃,如图所示.如果要围成面积是126m2的矩形花圃,请求出花圃的宽AB的长度.
A
B
D
C
分析:
设AB的长度为x m,
等量关系式:
S矩形ABCD =AB BC
则BC的长度为
(32-2x)m.
新知探究
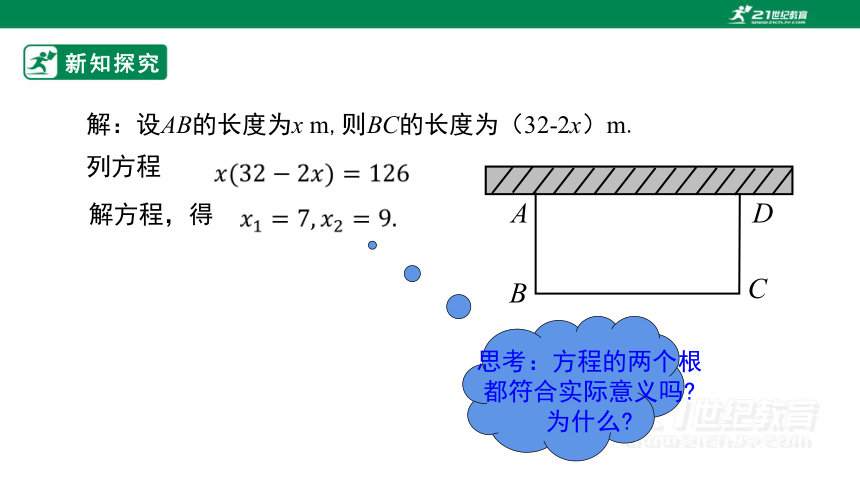
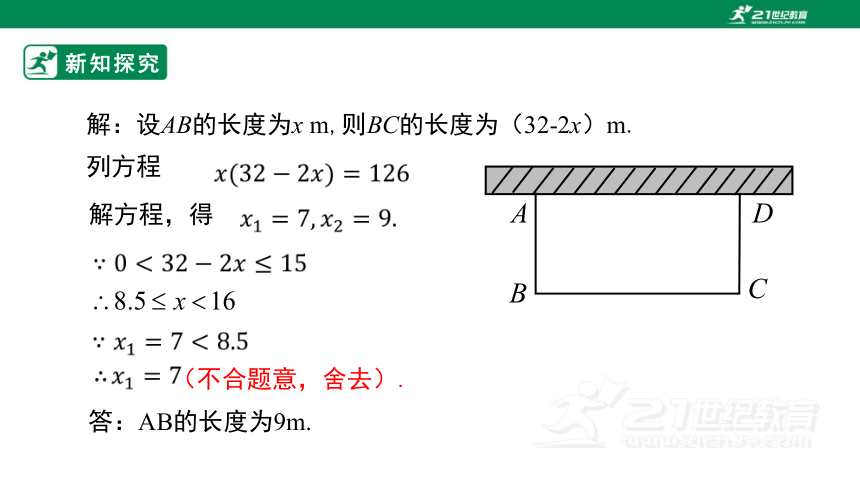
解:设AB的长度为x m,则BC的长度为(32-2x)m.
列方程
解方程,得
A
B
D
C
思考:方程的两个根都符合实际意义吗
为什么
新知探究
探究1 校园空地上有一面墙,长度为15m,用长为32m的篱笆和这面墙围成一个矩形花圃,如图所示.如果要围成面积是126m2的矩形花圃,请求出花圃的宽AB的长度.
A
B
D
C
新知探究
解:设AB的长度为x m,则BC的长度为(32-2x)m.
列方程
解方程,得
(不合题意,舍去).
答:AB的长度为9m.
A
B
D
C
新知小结
一般图形的面积问题,一般先设其中的一条边为x,用含x的代数式表示另一边,然后根据面积或周长公式列方程求解.最后,需要注意联系实际问题选择合适的解.
新知探究
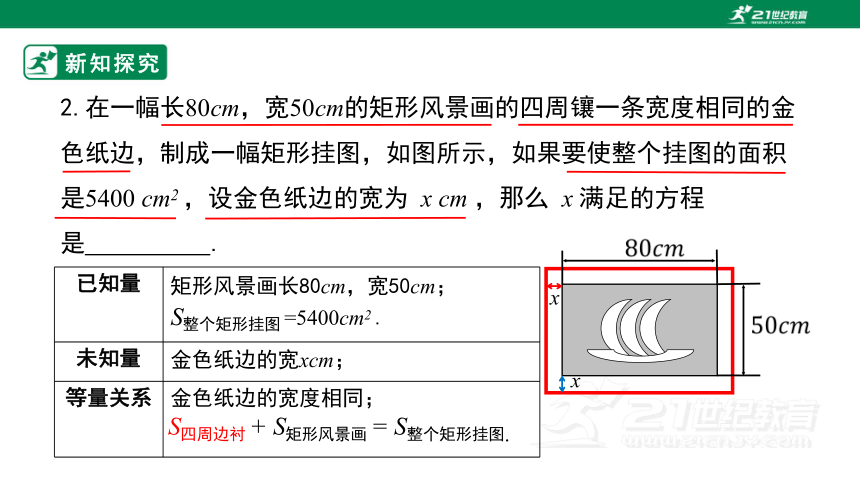
2.在一幅长80cm,宽50cm的矩形风景画的四周镶一条宽度相同的金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是5400 cm2 ,设金色纸边的宽为 x cm ,那么 x 满足的方程是 .
x
x
新知探究
2.在一幅长80cm,宽50cm的矩形风景画的四周镶一条宽度相同的金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是5400 cm2 ,设金色纸边的宽为 x cm ,那么 x 满足的方程是 .
已知量
未知量
等量关系
矩形风景画长80cm,宽50cm;
S整个矩形挂图 =5400cm2 .
S四周边衬 + S矩形风景画 = S整个矩形挂图.
x
x
金色纸边的宽度相同;
金色纸边的宽xcm;
新知探究
分析:
2.在一幅长80cm,宽50cm的矩形风景画的四周镶一条宽度相同的金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是5400 cm2 ,设金色纸边的宽为 x cm ,那么 x 满足的方程是 .
等量关系式
S四周边衬 + S矩形风景画 = S整个矩形挂图
(S1 +S2 +S3 +S4 +S5+S6 +S7 +S8 )+S矩形风景画
= S整个矩形挂图
S3
S1
S2
S7
S4
S5
S6
S8
新知探究
解:设金色纸边的宽为 .
列方程
整理,得
还有其他方法吗?
2.在一幅长80cm,宽50cm的矩形风景画的四周镶一条宽度相同的金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是5400 cm2 ,设金色纸边的宽为 x cm ,那么 x 满足的方程
是 .
x
x
新知探究
解:如图,设金色纸边的宽为
列方程
整理,得
2.在一幅长80cm,宽50cm的矩形风景画的四周镶一条宽度相同的金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是5400 cm2 ,设金色纸边的宽为 x cm ,那么 x 满足的方程是
.
x
x
则整个挂图的长为 ,宽为 .
新知探究
探究2 要设计一本书的封面,封面长 27 cm,宽 21 cm,正中央是一个与整个封面长宽比例相同的矩形,如果要使四周的彩色边衬所占面积是封面面积的四分之一,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度(结果保留小数点后一位)?
新知探究
S封面;
已知量
未知量
等量关系
探究2 要设计一本书的封面,封面长 27 cm,宽 21 cm,正中央是一个与整个封面长宽比例相同的矩形,如果要使四周的彩色边衬所占面积是封面面积的四分之一,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度(结果保留小数点后一位)?
封面长 27 cm,宽 21 cm;
正中央矩形的长和宽;
S四周彩色边衬;
上、下边衬的宽度;
正中央矩形的长宽之比 = 封面矩形的长宽之比;
上边衬宽度=下边衬宽度;
左边衬宽度=右边衬宽度.
左、右边衬的宽度;
新知探究
分析:
S四周彩色边衬 + S中央矩形 = S封面;
等量关系式
可得
关系式1:
关系式:2:
新知探究
分析:
思考:上、下边衬的宽度和左、右边衬的宽度之比也
是9 : 7吗?尝试计算一下。
探究2 要设计一本书的封面,封面长 27 cm,宽 21 cm,正中央是一个与整个封面长宽比例相同的矩形,如果要使四周的彩色边衬所占面积是封面面积的四分之一,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度(结果保留小数点后一位)?
封面的长宽之比是 27 : 21 = 9 : 7,
中央矩形的长宽之比是也应是 9 : 7.
新知探究
分析:
设中央矩形的长EF和宽EH分别是 9a cm和 7a cm .
则上、下边衬的宽度PE=FK= cm ;
则左、右边衬的宽度IE=HN= cm .
由此得上、下边衬的宽度和左、右边衬的宽度之比
PE : IE
新知探究
设上、下边衬的宽度PE、FK为 9x cm ,左、右边衬的宽度IE 、HN为 7x cm ,则中央的矩形的长EF为 cm ,宽EH为 cm .
列方程
分析:
新知探究
列方程
解:
设上、下边衬的宽均为 9x cm ,左、右边衬的宽均为 7x cm ,则中央的矩形的长为 cm ,宽为 cm .
封面的长宽之比是 27 : 21 = 9 : 7,中央矩形的长宽之比是也应是 9 : 7.设中央矩形的长和宽分别是 9a cm 和 7a cm ,由此得上、下边衬与左、右边衬的宽度之比是
新知探究
解方程,得
思考:方程的两个根都符合实际意义吗
为什么
整理,得
新知探究
探究2 要设计一本书的封面,封面长 27 cm,宽 21 cm,正中央是一个与整个封面长宽比例相同的矩形,如果要使四周的彩色边衬所占面积是封面面积的四分之一,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度(结果保留小数点后一位)?
27 - (上边衬的宽度+下边衬的宽度)>0
且 21 -(左边衬的宽度+右边衬的宽度)>0
课堂练习
解方程,得
整理,得
而
(不合题意,舍去).
新知探究
答:上、下边衬的宽约为 1. 8 cm,左、右边衬的宽约为 1. 4 cm.
新知探究
思考: 如果换一种未知数的设法,是否可以更简单地解决上面的问题?请你试一试.
探究2 要设计一本书的封面,封面长 27 cm,宽 21 cm,正中央是一个与整个封面长宽比例相同的矩形,如果要使四周的彩色边衬所占面积是封面面积的四分之一,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度(结果保留小数点后一位)?
新知探究
分析:中央矩形的长宽之比EF:EH= 9 : 7.
设中央矩形的长EF、宽EH分别为 9x cm ,7x cm .
那么S中央矩形EFGH 可以表示为_________cm2.
上、下边衬的宽PE可以表示为___________cm;
左、右边衬的宽IE可以表示为___________cm .
9x · 7x
探究2 要设计一本书的封面,封面长 27 cm,宽 21 cm,正中央是一个与整个封面长宽比例相同的矩形,如果要使四周的彩色边衬所占面积是封面面积的四分之一,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度(结果保留小数点后一位)?
新知探究
封面的长宽之比是 27 : 21 = 9 : 7,中央矩形的长宽之比是也应是 9 : 7.设中央矩形的长、宽分别为 9x cm ,7x cm .
分析:等量关系式
列方程
解方程,得
(不合题意,舍去).
答:上、下边衬的宽约为 1. 8 cm ,左、右边衬的宽约为 1. 4 cm .
解:
课堂总结
2.如何找出等量关系?
1.如何处理未知量?
直接利用题目中给出的等量关系;间接找出等价的等量关系.
可以根据问题直接设未知量;也可以根据题目间接设未知量.
3.注意结果的实际意义,要进行检验.
课堂总结
列方程依据
常见几何图形面积是等量关系.
常见类型
课本封面的面积问题
一般图形的面积问题
新知练习
A.10 cm B.13 cm C.14 cm D.16 cm
1.将一块正方形铁皮的四个角各剪去一个边长为 3 cm 的小正方形,做成一个无盖的盒子,已知盒子的容积为 300 cm3,则原铁皮的边长为( )
D
解:设正方形铁皮的边长是 x 厘米,
则没有盖的长方体盒子的长、宽为(x-3×2)厘米,高为3厘米,
根据题意列方程得 (x-3×2)(x-3×2)×3=300,
解得 x1=16,x2=-4(不合题意,舍去);
所以正方形铁皮的边长是16厘米.
新知练习
2.一个直角三角形的两条直角边的和是 14 cm,面积是 24 cm2.求两条直角边的长.
解:设一条直角边的长为 x cm,则另一条直角边的长为 (14-x) cm,
可得到 x(14-x)=24,
方程可化为 x2-14x+48=0,解得 x1=6,x2=8.
当 x=6 时,14-x=14-6=8;
当 x=8 时,14-x=14-8=6.
所以两条直角边的长分别为 8 cm和 6 cm.
新知练习
20
32
x
x
解法一:设道路的宽为 x 米,则由题意得
3.如图,在一块宽为 20 m,长为 32 m 的矩形地面上修筑同样宽的两条道路,余下的部分种上草坪,要使草坪的面积为 540 m2,求道路的宽为多少.
整理,得 x2-52x+100=0,
解得 x1=2,x2=50,
当 x=50 时,32-x=-18,不合题意,舍去.
所以x=2.
答:道路的宽为2米.
还有其他解法吗?
新知练习
20
32
x
x
解法二:设道路的宽为 x 米,则由题意得
20-x
32-x
(32-x)(20-x)=540,
整理,得 x2-52x+100=0,
解得 x1=2,x2=50,
当 x=50 时,32-x=-18,不合题意,舍去.
所以x=2.
答:道路的宽为2米.
3.如图,在一块宽为 20 m,长为 32 m 的矩形地面上修筑同样宽的两条道路,余下的部分种上草坪,要使草坪的面积为 540 m2,求道路的宽为多少.
新知练习
4.在长为 160 m ,宽为 100 m的矩形地面上修筑同样宽的道路,余下的部分种上草坪,要使草坪的面积为 13500 m2,求这种方案下的道路的宽为多少.
解:设道路的宽为 x 米,
(160-x)(100-x)=13500,
可列方程为
整理,得 x2-260x+2500=0,
解得 x1=10,x2=250(不合题意,舍去),
所以x=10,
即道路的宽为10米.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
21.3实际问题与一元二次方程(3)
——几何问题
人教版九年级上册
教学目标
1.能正确利用一元二次方程的相关知识解决几何图形的面积问题.
2.经历将实际的几何问题转化为数学问题的过程,进一步深入体会一元二次方程在实际生活中的应用,提高数学应用意识.
知识回顾
实际问题
已知量、未知量、
等量关系
数学问题
一元二次方程
解的合理性
方程的解
作 答
求出
验证
符合实际
不合实际
建立
抽象
分析
如何用一元二次方程模型解决实际问题?
新知导入
A
新知探究
探究1 校园空地上有一面墙,长度为15m,用长为32m的篱笆和这面墙围成一个矩形花圃,如图所示.如果要围成面积是126m2的矩形花圃,请求出花圃的宽AB的长度.
A
B
D
C
分析:
设AB的长度为x m,
等量关系式:
S矩形ABCD =AB BC
则BC的长度为
(32-2x)m.
新知探究
解:设AB的长度为x m,则BC的长度为(32-2x)m.
列方程
解方程,得
A
B
D
C
思考:方程的两个根都符合实际意义吗
为什么
新知探究
探究1 校园空地上有一面墙,长度为15m,用长为32m的篱笆和这面墙围成一个矩形花圃,如图所示.如果要围成面积是126m2的矩形花圃,请求出花圃的宽AB的长度.
A
B
D
C
新知探究
解:设AB的长度为x m,则BC的长度为(32-2x)m.
列方程
解方程,得
(不合题意,舍去).
答:AB的长度为9m.
A
B
D
C
新知小结
一般图形的面积问题,一般先设其中的一条边为x,用含x的代数式表示另一边,然后根据面积或周长公式列方程求解.最后,需要注意联系实际问题选择合适的解.
新知探究
2.在一幅长80cm,宽50cm的矩形风景画的四周镶一条宽度相同的金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是5400 cm2 ,设金色纸边的宽为 x cm ,那么 x 满足的方程是 .
x
x
新知探究
2.在一幅长80cm,宽50cm的矩形风景画的四周镶一条宽度相同的金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是5400 cm2 ,设金色纸边的宽为 x cm ,那么 x 满足的方程是 .
已知量
未知量
等量关系
矩形风景画长80cm,宽50cm;
S整个矩形挂图 =5400cm2 .
S四周边衬 + S矩形风景画 = S整个矩形挂图.
x
x
金色纸边的宽度相同;
金色纸边的宽xcm;
新知探究
分析:
2.在一幅长80cm,宽50cm的矩形风景画的四周镶一条宽度相同的金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是5400 cm2 ,设金色纸边的宽为 x cm ,那么 x 满足的方程是 .
等量关系式
S四周边衬 + S矩形风景画 = S整个矩形挂图
(S1 +S2 +S3 +S4 +S5+S6 +S7 +S8 )+S矩形风景画
= S整个矩形挂图
S3
S1
S2
S7
S4
S5
S6
S8
新知探究
解:设金色纸边的宽为 .
列方程
整理,得
还有其他方法吗?
2.在一幅长80cm,宽50cm的矩形风景画的四周镶一条宽度相同的金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是5400 cm2 ,设金色纸边的宽为 x cm ,那么 x 满足的方程
是 .
x
x
新知探究
解:如图,设金色纸边的宽为
列方程
整理,得
2.在一幅长80cm,宽50cm的矩形风景画的四周镶一条宽度相同的金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是5400 cm2 ,设金色纸边的宽为 x cm ,那么 x 满足的方程是
.
x
x
则整个挂图的长为 ,宽为 .
新知探究
探究2 要设计一本书的封面,封面长 27 cm,宽 21 cm,正中央是一个与整个封面长宽比例相同的矩形,如果要使四周的彩色边衬所占面积是封面面积的四分之一,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度(结果保留小数点后一位)?
新知探究
S封面;
已知量
未知量
等量关系
探究2 要设计一本书的封面,封面长 27 cm,宽 21 cm,正中央是一个与整个封面长宽比例相同的矩形,如果要使四周的彩色边衬所占面积是封面面积的四分之一,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度(结果保留小数点后一位)?
封面长 27 cm,宽 21 cm;
正中央矩形的长和宽;
S四周彩色边衬;
上、下边衬的宽度;
正中央矩形的长宽之比 = 封面矩形的长宽之比;
上边衬宽度=下边衬宽度;
左边衬宽度=右边衬宽度.
左、右边衬的宽度;
新知探究
分析:
S四周彩色边衬 + S中央矩形 = S封面;
等量关系式
可得
关系式1:
关系式:2:
新知探究
分析:
思考:上、下边衬的宽度和左、右边衬的宽度之比也
是9 : 7吗?尝试计算一下。
探究2 要设计一本书的封面,封面长 27 cm,宽 21 cm,正中央是一个与整个封面长宽比例相同的矩形,如果要使四周的彩色边衬所占面积是封面面积的四分之一,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度(结果保留小数点后一位)?
封面的长宽之比是 27 : 21 = 9 : 7,
中央矩形的长宽之比是也应是 9 : 7.
新知探究
分析:
设中央矩形的长EF和宽EH分别是 9a cm和 7a cm .
则上、下边衬的宽度PE=FK= cm ;
则左、右边衬的宽度IE=HN= cm .
由此得上、下边衬的宽度和左、右边衬的宽度之比
PE : IE
新知探究
设上、下边衬的宽度PE、FK为 9x cm ,左、右边衬的宽度IE 、HN为 7x cm ,则中央的矩形的长EF为 cm ,宽EH为 cm .
列方程
分析:
新知探究
列方程
解:
设上、下边衬的宽均为 9x cm ,左、右边衬的宽均为 7x cm ,则中央的矩形的长为 cm ,宽为 cm .
封面的长宽之比是 27 : 21 = 9 : 7,中央矩形的长宽之比是也应是 9 : 7.设中央矩形的长和宽分别是 9a cm 和 7a cm ,由此得上、下边衬与左、右边衬的宽度之比是
新知探究
解方程,得
思考:方程的两个根都符合实际意义吗
为什么
整理,得
新知探究
探究2 要设计一本书的封面,封面长 27 cm,宽 21 cm,正中央是一个与整个封面长宽比例相同的矩形,如果要使四周的彩色边衬所占面积是封面面积的四分之一,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度(结果保留小数点后一位)?
27 - (上边衬的宽度+下边衬的宽度)>0
且 21 -(左边衬的宽度+右边衬的宽度)>0
课堂练习
解方程,得
整理,得
而
(不合题意,舍去).
新知探究
答:上、下边衬的宽约为 1. 8 cm,左、右边衬的宽约为 1. 4 cm.
新知探究
思考: 如果换一种未知数的设法,是否可以更简单地解决上面的问题?请你试一试.
探究2 要设计一本书的封面,封面长 27 cm,宽 21 cm,正中央是一个与整个封面长宽比例相同的矩形,如果要使四周的彩色边衬所占面积是封面面积的四分之一,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度(结果保留小数点后一位)?
新知探究
分析:中央矩形的长宽之比EF:EH= 9 : 7.
设中央矩形的长EF、宽EH分别为 9x cm ,7x cm .
那么S中央矩形EFGH 可以表示为_________cm2.
上、下边衬的宽PE可以表示为___________cm;
左、右边衬的宽IE可以表示为___________cm .
9x · 7x
探究2 要设计一本书的封面,封面长 27 cm,宽 21 cm,正中央是一个与整个封面长宽比例相同的矩形,如果要使四周的彩色边衬所占面积是封面面积的四分之一,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度(结果保留小数点后一位)?
新知探究
封面的长宽之比是 27 : 21 = 9 : 7,中央矩形的长宽之比是也应是 9 : 7.设中央矩形的长、宽分别为 9x cm ,7x cm .
分析:等量关系式
列方程
解方程,得
(不合题意,舍去).
答:上、下边衬的宽约为 1. 8 cm ,左、右边衬的宽约为 1. 4 cm .
解:
课堂总结
2.如何找出等量关系?
1.如何处理未知量?
直接利用题目中给出的等量关系;间接找出等价的等量关系.
可以根据问题直接设未知量;也可以根据题目间接设未知量.
3.注意结果的实际意义,要进行检验.
课堂总结
列方程依据
常见几何图形面积是等量关系.
常见类型
课本封面的面积问题
一般图形的面积问题
新知练习
A.10 cm B.13 cm C.14 cm D.16 cm
1.将一块正方形铁皮的四个角各剪去一个边长为 3 cm 的小正方形,做成一个无盖的盒子,已知盒子的容积为 300 cm3,则原铁皮的边长为( )
D
解:设正方形铁皮的边长是 x 厘米,
则没有盖的长方体盒子的长、宽为(x-3×2)厘米,高为3厘米,
根据题意列方程得 (x-3×2)(x-3×2)×3=300,
解得 x1=16,x2=-4(不合题意,舍去);
所以正方形铁皮的边长是16厘米.
新知练习
2.一个直角三角形的两条直角边的和是 14 cm,面积是 24 cm2.求两条直角边的长.
解:设一条直角边的长为 x cm,则另一条直角边的长为 (14-x) cm,
可得到 x(14-x)=24,
方程可化为 x2-14x+48=0,解得 x1=6,x2=8.
当 x=6 时,14-x=14-6=8;
当 x=8 时,14-x=14-8=6.
所以两条直角边的长分别为 8 cm和 6 cm.
新知练习
20
32
x
x
解法一:设道路的宽为 x 米,则由题意得
3.如图,在一块宽为 20 m,长为 32 m 的矩形地面上修筑同样宽的两条道路,余下的部分种上草坪,要使草坪的面积为 540 m2,求道路的宽为多少.
整理,得 x2-52x+100=0,
解得 x1=2,x2=50,
当 x=50 时,32-x=-18,不合题意,舍去.
所以x=2.
答:道路的宽为2米.
还有其他解法吗?
新知练习
20
32
x
x
解法二:设道路的宽为 x 米,则由题意得
20-x
32-x
(32-x)(20-x)=540,
整理,得 x2-52x+100=0,
解得 x1=2,x2=50,
当 x=50 时,32-x=-18,不合题意,舍去.
所以x=2.
答:道路的宽为2米.
3.如图,在一块宽为 20 m,长为 32 m 的矩形地面上修筑同样宽的两条道路,余下的部分种上草坪,要使草坪的面积为 540 m2,求道路的宽为多少.
新知练习
4.在长为 160 m ,宽为 100 m的矩形地面上修筑同样宽的道路,余下的部分种上草坪,要使草坪的面积为 13500 m2,求这种方案下的道路的宽为多少.
解:设道路的宽为 x 米,
(160-x)(100-x)=13500,
可列方程为
整理,得 x2-260x+2500=0,
解得 x1=10,x2=250(不合题意,舍去),
所以x=10,
即道路的宽为10米.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
