21.3实际问题与一元二次方程(4)——利润问题 课件(22张PPT)
文档属性
| 名称 | 21.3实际问题与一元二次方程(4)——利润问题 课件(22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-14 13:38:41 | ||
图片预览








文档简介
(共22张PPT)
21.3实际问题与一元二次方程(4)
利润问题
人教版九年级上册
教学目标
1.能利用一元二次方程模型解决利润问题.
2.经历建立方程模型解决问题的过程,体会数学建模的思想.
知识回顾
1.某件商品的进价是100元,售价是150元,则该
件商品的利润为___________元;
2.某商店销售一批玩具,每件利润是2元,销售量为20件,则总利润为___________元.
50
单件利润=售价-进价
40
总利润=单件利润×销售量
=150-100
=2×20
新知导入
例1某种服装每件盈利44元,平均每天可销售20件.
每降价1元,每天可多售出5件.
(1)若降价1元,则每件盈利_________元,每天可售
出_______件,每天盈利________元;
(2)若降价6元,则每件盈利________元,每天可售
出________件,每天盈利________元;
43
25
1075
38
50
1900
43×25
38×50
20
20+5×6
多售出5×1件
降价6元
多售出5×6件
降价1元
+5×1
总利润=单件利润×销售量
新知探究
例1某种服装每件盈利44元,平均每天销售20件.
每降价1元,每天可多售出5件.
(3)如果每天要盈利1600元,那么每件应降价多少元?
列方程解决实际问题的一般步骤:
①审题;
②设未知数;
③列方程;
④解方程;.
⑤检验;
⑥答.
新知探究
(3)解:设每件应降价x元.根据题意,得
解得 x1=4,x2=36.
(44-x)(20+5x)=1600
答:每件应降价4或36元.
都符合题意
新知小结
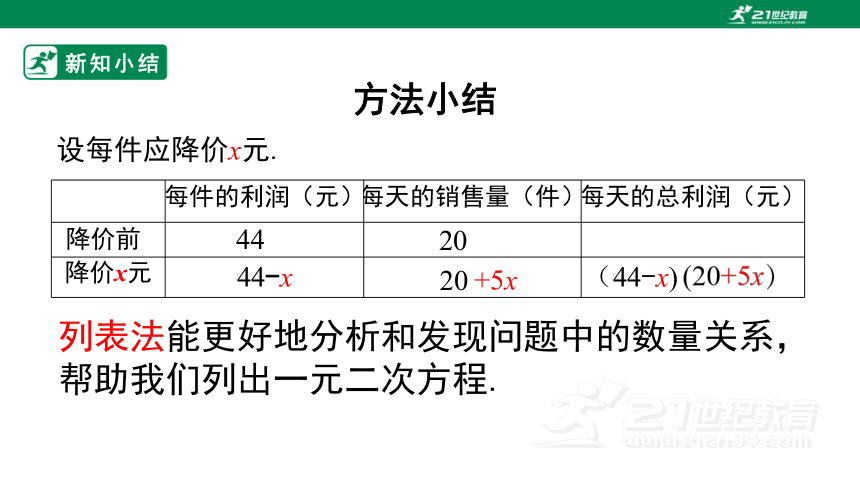
设每件应降价x元.
列表法能更好地分析和发现问题中的数量关系,帮助我们列出一元二次方程.
每件的利润(元) 每天的销售量(件) 每天的总利润(元)
降价x元
44-x
+5x
(44-x)
20
降价前
20
44
方法小结
新知练习
练习 某商店准备进一批季节性小家电,进价40元.经市场预测,销售定价为52元时,可售出180个,定价每增加1元,销售量就减少10个.因受库存的影响,每批次进货个数不得超过190个,商店若准备获利2000元,则应定价为多少元?
设定价增加x元.列表分析:
每个的利润(元) 销售量(个) 总利润(元)
涨价前
涨价x元后
52-40
180
52-40+x
-10x
(180-10x)
(52-40+x)(180-10x)=2000
定价增加了x元,销售量就减少10x个
销售定价为52元
进价40元
180
(52-40+x)
定价增加了 个1元,销售量就减少 个10
180
新知练习
解:设定价增加x元.根据题意,得
(52-40+x)(180-10x)=2000
解得 x1=-2,x2=8.
当x=-2时,销售量为180+20=200>190,
不合题意,舍去;
答:应定价为60元.
因为每批次进货个数不得超过190个,
若直接设定价为x元,应如何列方程呢?
当x=8时,销售量为180-80=100<190,符合题意.
所以定价为52+8=60(元).
新知练习
设定价为x元.
定价(元) 每个的利润(元) 销售量(个) 总利润(元)
52-40
180
x -40
180-10(x-52)
[180-10(x-52)]
(x-40)[180-10(x-52)]=2000
练习 某商店准备进一批季节性小家电,进价40元.经市场预测,销售定价为52元时,可售出180个,定价每增加1元,销售量就减少10个.因受库存的影响,每批次进货个数不得超过190个,商店若准备获利2000元,则应定价为多少元?
定价增加了(x-52)元,销售量就减少10(x-52)个
定价为52元
(x -40)
52
x
新知练习
解:设应定价为x元.根据题意,得
解得 x1=60,x2=50
当x=50时,销售量为180+20=200>190,
不合题意,舍去;
答:应定价为60元.
(x-40)[180-10(x-52)]=2000
因为每批次进货个数不得超过190个,
当x=60时,销售量为180-80=100<190,
符合题意.
新知探究
例2 某水泥代销点销售某种水泥,每吨进价为250元.
每吨销售价定为290元时,平均每天可售出16吨.
若每吨售价每降低5元,则平均每天能多售出4吨.
问:每吨水泥的实际售价定为多少元时,每天的
销售利润平均可达720元?
分析:设每吨应降价x元.
每吨的利润(元) 每天的销售量(吨) 每天的总利润(元)
降价前
降价后
40
16
40-x
16
+4×
=720
售价降低 个5元,就多售出 个4吨
新知探究
解得 x1= x2=10,
所以290-x=290-10=280.
答:每吨水泥的实际售价定为280元时,每天的销售利润平均可达720元.
解:设每吨应降价x元.根据题意,得
符合题意.
新知探究
例2 某水泥代销点销售某种水泥,每吨进价为250元.
若每吨销售价定为290元时,平均每天可售出16吨.
若每吨售价每降低5元,则平均每天能多售出4吨.
问:每吨水泥的实际售价定为多少元时,每天的
销售利润平均可达720元?
设每吨应降价x元,得
另一个角度理解
新知练习
某西瓜经营户以2元/kg的价格购进一批良种西瓜,以3元/kg的价格出售,每天可售出200 kg,为了促销,该经营户决定降价销售,经调查发现,这种良种西瓜每降价0.1元/kg,每天可多售出40 kg,另外每天的房租等固定成本共24元,该经营户要想每天盈利200元,应将每千克良种西瓜降价多少元?
解:设每千克良种西瓜降价x元,则有
解得x1=0.2,x2=0.3.
∵为了促销,∴x=0.3.
答:要想每天盈利200元,应将每千克良种西瓜降价0.3元.
两个结果都要吗?
新知小结
抓住关键语句“每…,每…”,采用从特殊到一般的方法,找出价格波动与单位利润、销售量之间的变化规律,再根据“总利润=单位利润×销售量”列出一元二次方程.
课堂总结
本节课学习了利用一元二次方程模型解决利润问题.
实际问题
(利润问题)
一元二次方程
一元二次方程的解
实际问题
的答案
设未知数,根据“单位利润×销售量=总利润”列方程
抽象为方程模型
解方程
回归于实际问题
检验
课堂练习
1.某商品的进价为5元,当售价为x元时,此时能销售该商品(x+5)个,此时获利144元,则该商品的售价为 元.
2.某商品的进价为每件40元.当售价为每件60元时,每星期可卖出300件,现需降价处理,为占有市场份额,且经市场调查:每降价1元,每星期可多卖出20件.现在要使利润为6120元,每件商品应降价 元.
13
3
课堂练习
3.山西特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克.后来经过市场调查发现,单价每降低2元,则平均每天的销售量可增加20千克.若该专卖店销售这种核桃想要平均每天获利2240元,请回答:
(1)每千克核桃应降价多少元?
(2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?
课堂练习
(1)设每千克核桃应降价x元,根据题意,得
(60-x-40)(100+×20)=2240.化简,得x2-10x+24=0,解得x1=4,x2=6,
答:每千克核桃应降价4元或6元;
(2)由(1)可知每千克核桃可降价4元或6元,因为要尽可能让利于顾客,所以每千克核桃应降价6元,此时,售价为60-6=54(元),×100%=90%.
答:该店应按原售价的九折出售.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
21.3实际问题与一元二次方程(4)
利润问题
人教版九年级上册
教学目标
1.能利用一元二次方程模型解决利润问题.
2.经历建立方程模型解决问题的过程,体会数学建模的思想.
知识回顾
1.某件商品的进价是100元,售价是150元,则该
件商品的利润为___________元;
2.某商店销售一批玩具,每件利润是2元,销售量为20件,则总利润为___________元.
50
单件利润=售价-进价
40
总利润=单件利润×销售量
=150-100
=2×20
新知导入
例1某种服装每件盈利44元,平均每天可销售20件.
每降价1元,每天可多售出5件.
(1)若降价1元,则每件盈利_________元,每天可售
出_______件,每天盈利________元;
(2)若降价6元,则每件盈利________元,每天可售
出________件,每天盈利________元;
43
25
1075
38
50
1900
43×25
38×50
20
20+5×6
多售出5×1件
降价6元
多售出5×6件
降价1元
+5×1
总利润=单件利润×销售量
新知探究
例1某种服装每件盈利44元,平均每天销售20件.
每降价1元,每天可多售出5件.
(3)如果每天要盈利1600元,那么每件应降价多少元?
列方程解决实际问题的一般步骤:
①审题;
②设未知数;
③列方程;
④解方程;.
⑤检验;
⑥答.
新知探究
(3)解:设每件应降价x元.根据题意,得
解得 x1=4,x2=36.
(44-x)(20+5x)=1600
答:每件应降价4或36元.
都符合题意
新知小结
设每件应降价x元.
列表法能更好地分析和发现问题中的数量关系,帮助我们列出一元二次方程.
每件的利润(元) 每天的销售量(件) 每天的总利润(元)
降价x元
44-x
+5x
(44-x)
20
降价前
20
44
方法小结
新知练习
练习 某商店准备进一批季节性小家电,进价40元.经市场预测,销售定价为52元时,可售出180个,定价每增加1元,销售量就减少10个.因受库存的影响,每批次进货个数不得超过190个,商店若准备获利2000元,则应定价为多少元?
设定价增加x元.列表分析:
每个的利润(元) 销售量(个) 总利润(元)
涨价前
涨价x元后
52-40
180
52-40+x
-10x
(180-10x)
(52-40+x)(180-10x)=2000
定价增加了x元,销售量就减少10x个
销售定价为52元
进价40元
180
(52-40+x)
定价增加了 个1元,销售量就减少 个10
180
新知练习
解:设定价增加x元.根据题意,得
(52-40+x)(180-10x)=2000
解得 x1=-2,x2=8.
当x=-2时,销售量为180+20=200>190,
不合题意,舍去;
答:应定价为60元.
因为每批次进货个数不得超过190个,
若直接设定价为x元,应如何列方程呢?
当x=8时,销售量为180-80=100<190,符合题意.
所以定价为52+8=60(元).
新知练习
设定价为x元.
定价(元) 每个的利润(元) 销售量(个) 总利润(元)
52-40
180
x -40
180-10(x-52)
[180-10(x-52)]
(x-40)[180-10(x-52)]=2000
练习 某商店准备进一批季节性小家电,进价40元.经市场预测,销售定价为52元时,可售出180个,定价每增加1元,销售量就减少10个.因受库存的影响,每批次进货个数不得超过190个,商店若准备获利2000元,则应定价为多少元?
定价增加了(x-52)元,销售量就减少10(x-52)个
定价为52元
(x -40)
52
x
新知练习
解:设应定价为x元.根据题意,得
解得 x1=60,x2=50
当x=50时,销售量为180+20=200>190,
不合题意,舍去;
答:应定价为60元.
(x-40)[180-10(x-52)]=2000
因为每批次进货个数不得超过190个,
当x=60时,销售量为180-80=100<190,
符合题意.
新知探究
例2 某水泥代销点销售某种水泥,每吨进价为250元.
每吨销售价定为290元时,平均每天可售出16吨.
若每吨售价每降低5元,则平均每天能多售出4吨.
问:每吨水泥的实际售价定为多少元时,每天的
销售利润平均可达720元?
分析:设每吨应降价x元.
每吨的利润(元) 每天的销售量(吨) 每天的总利润(元)
降价前
降价后
40
16
40-x
16
+4×
=720
售价降低 个5元,就多售出 个4吨
新知探究
解得 x1= x2=10,
所以290-x=290-10=280.
答:每吨水泥的实际售价定为280元时,每天的销售利润平均可达720元.
解:设每吨应降价x元.根据题意,得
符合题意.
新知探究
例2 某水泥代销点销售某种水泥,每吨进价为250元.
若每吨销售价定为290元时,平均每天可售出16吨.
若每吨售价每降低5元,则平均每天能多售出4吨.
问:每吨水泥的实际售价定为多少元时,每天的
销售利润平均可达720元?
设每吨应降价x元,得
另一个角度理解
新知练习
某西瓜经营户以2元/kg的价格购进一批良种西瓜,以3元/kg的价格出售,每天可售出200 kg,为了促销,该经营户决定降价销售,经调查发现,这种良种西瓜每降价0.1元/kg,每天可多售出40 kg,另外每天的房租等固定成本共24元,该经营户要想每天盈利200元,应将每千克良种西瓜降价多少元?
解:设每千克良种西瓜降价x元,则有
解得x1=0.2,x2=0.3.
∵为了促销,∴x=0.3.
答:要想每天盈利200元,应将每千克良种西瓜降价0.3元.
两个结果都要吗?
新知小结
抓住关键语句“每…,每…”,采用从特殊到一般的方法,找出价格波动与单位利润、销售量之间的变化规律,再根据“总利润=单位利润×销售量”列出一元二次方程.
课堂总结
本节课学习了利用一元二次方程模型解决利润问题.
实际问题
(利润问题)
一元二次方程
一元二次方程的解
实际问题
的答案
设未知数,根据“单位利润×销售量=总利润”列方程
抽象为方程模型
解方程
回归于实际问题
检验
课堂练习
1.某商品的进价为5元,当售价为x元时,此时能销售该商品(x+5)个,此时获利144元,则该商品的售价为 元.
2.某商品的进价为每件40元.当售价为每件60元时,每星期可卖出300件,现需降价处理,为占有市场份额,且经市场调查:每降价1元,每星期可多卖出20件.现在要使利润为6120元,每件商品应降价 元.
13
3
课堂练习
3.山西特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克.后来经过市场调查发现,单价每降低2元,则平均每天的销售量可增加20千克.若该专卖店销售这种核桃想要平均每天获利2240元,请回答:
(1)每千克核桃应降价多少元?
(2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?
课堂练习
(1)设每千克核桃应降价x元,根据题意,得
(60-x-40)(100+×20)=2240.化简,得x2-10x+24=0,解得x1=4,x2=6,
答:每千克核桃应降价4元或6元;
(2)由(1)可知每千克核桃可降价4元或6元,因为要尽可能让利于顾客,所以每千克核桃应降价6元,此时,售价为60-6=54(元),×100%=90%.
答:该店应按原售价的九折出售.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
