11.3多边形及其内角和 同步自主提升训练题 2023—2024学年人教版数学八年级上册(含答案)
文档属性
| 名称 | 11.3多边形及其内角和 同步自主提升训练题 2023—2024学年人教版数学八年级上册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 225.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-14 12:32:07 | ||
图片预览




文档简介
2023-2024学年人教版八年级数学上册《11.3多边形及其内角和》
同步自主提升训练题(附答案)
一、单选题
1.四边形的内角和与外角和的数量关系,正确的是( )
A.内角和比外角和大180° B.外角和比内角和大180°
C.内角和比外角和大360° D.内角和与外角和相等
2.正八边形每个内角度数为( )
A.120° B.135° C.150° D.160°
3.若一个多边形截去一个角后变成了六边形,则原来多边形的边数可能是( )
A.5或6 B.6或7 C.5或6或7 D.6或7或8
4.多边形每一个内角都等于150°,则从该多边形一个顶点出发,可引出对角线的条数为( )
A.9条 B.8条 C.7条 D.6条
5.已知一个多边形的内角和与外角和的和为2160°,这个多边形的边数为( )
A.9 B.10 C.11 D.12
6.如图,五边形中,,CP,DP分别平分,,则( )
A.60° B.72° C.70° D.78°
7.一多边形的每一个内角都等于它相邻外角的4倍,则该多边形的内角和是( )
A.360° B.900° C.1440° D.1800°
8.如图,( )度.
A.180 B.270 C.360 D.540
二、填空题
9.n边形的内角和为1440°,则n= .
10.用三个正多边形镶嵌,已知其中两个的边数均为5,则第三个正多边形的边数为 .
11.在计算某n边形的内角和时,不小心少算了一个内角,得到和为,这个角的大小是 .
12.一个多边形截去一个角后,形成的另一个多边形的内角和是1440°.则原来多边形的边数是 .
13.已知某正多边形每一个外角都等于,则从此多边形一个顶点出发,可以引的对角线的条数是 条
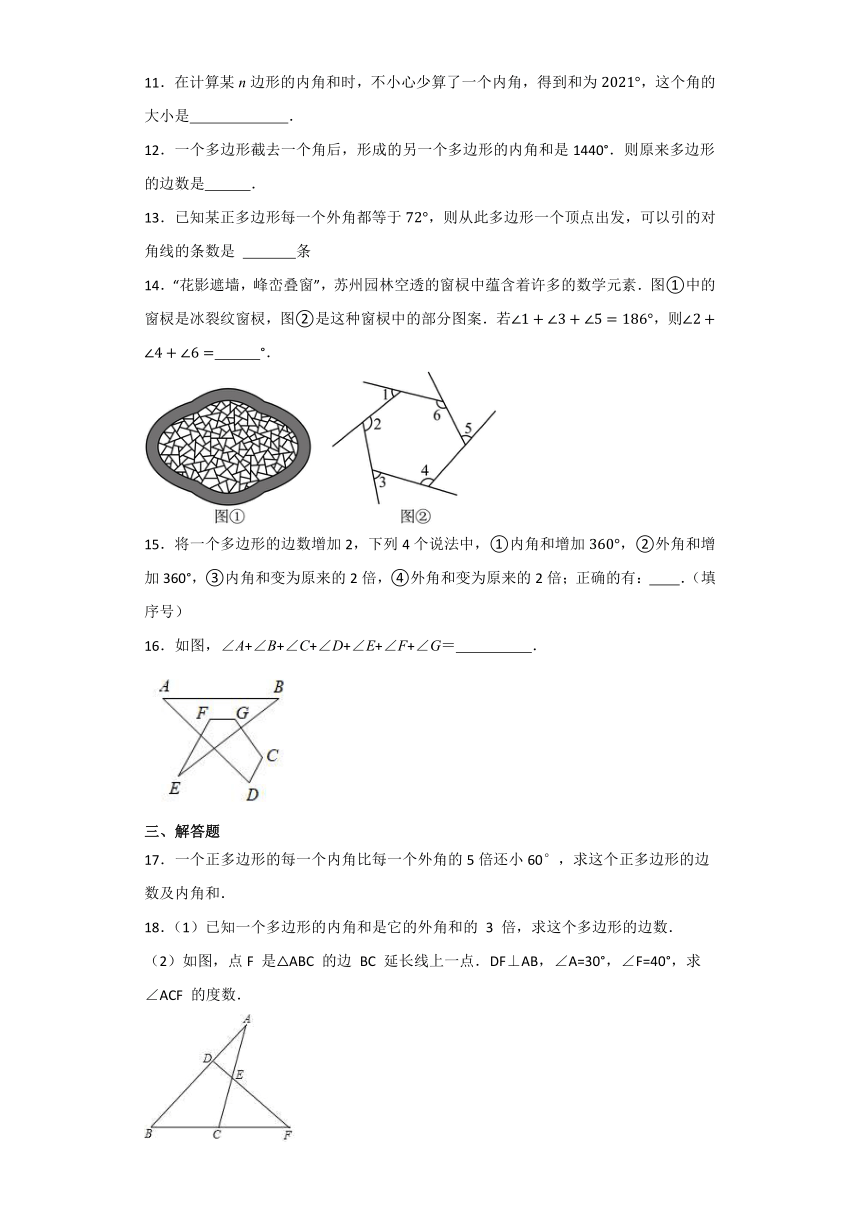
14.“花影遮墙,峰峦叠窗”,苏州园林空透的窗棂中蕴含着许多的数学元素.图①中的窗棂是冰裂纹窗棂,图②是这种窗棂中的部分图案.若,则 °.
15.将一个多边形的边数增加2,下列4个说法中,①内角和增加,②外角和增加360°,③内角和变为原来的2倍,④外角和变为原来的2倍;正确的有: .(填序号)
16.如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G= .
三、解答题
17.一个正多边形的每一个内角比每一个外角的5倍还小60°,求这个正多边形的边数及内角和.
18.(1)已知一个多边形的内角和是它的外角和的 3 倍,求这个多边形的边数.
(2)如图,点F 是△ABC 的边 BC 延长线上一点.DF⊥AB,∠A=30°,∠F=40°,求∠ACF 的度数.
19.小明家准备用正方形地板砖铺设客厅,客厅的长为6.4 m,宽为4.8 m.装修工人提出两种铺设方案:第一种方案是铺设80 cm×80 cm的地板砖,每块40元;第二种方案是铺设60 cm×60 cm的地板砖,每块25元;第三种方案是铺设40 cm×40 cm的地板砖,每块15元.你能从中帮他选一种材料的费用少且铺得又整齐的方案吗?
20.阅读佳佳与明明的对话,解决下列问题:
佳佳:我把一个多边形的各内角相加,所得的和为;
明明:什么?不可能的!虽然你的运算正确,但是你错把一个外角当成一个内角了!
(1)“多边形内角和为”,为什么不可能?
(2)佳佳求的是几边形的内角和?
(3)错当成内角的那个外角为多少度?
21.如图,在四边形ABCD中,∠ABC、∠ADC的平分线分别与CD、AB相交于点E、F.
(1)若∠A与∠C互补,∠CDF=40°,求∠ABE的度数.
(2)若∠A=∠C=90°,试判断DF与BE有怎样的位置关系,并请说明理由.
22.(1)已知:如图1,P为△ADC内一点,DP、CP分别平分∠ADC和∠ACD,如果∠A=90°,那么∠P=______°;如果∠A=x°,则∠P=____________°;(答案直接填在题中横线上)
(2)如图2,P为四边形ABCD内一点,DP、CP分别平分∠ADC和∠BCD,试探究∠P与∠A+∠B的数量关系,并写出你的探索过程;
(3)如图3,P为五边形ABCDE内一点,DP、CP分别平分∠EDC和∠BCD,请直接写出∠P与∠A+∠B+∠E的数量关系:________________;
(4)若P为n边形A1A2A3…An内一点,PA1平分∠AnA1A2,PA2平分∠A1A2A3,请直接写出∠P与∠A3+A4+A5+…∠An的数量关系:__________________________.(用含n的代数式表示)
参考答案
1.解:A.四边形的内角和与外角和相等,都等于360°,故本选项表述错误;
B.四边形的内角和与外角和相等,都等于360°,故本选项表述错误;
C.六四边形的内角和与外角和相等,都等于360°,故本选项表述错误;
D.四边形的内角和与外角和相等,都等于360°,故本选项表述正确.
故选:D.
2.解:∵正多边形的每一个内角相等,则对应的外角也相等,
一个外角等于:
∴内角为
故选B
3.解:如图,原来多边形的边数可能是5,6,7.
故选C
4.解:∵多边形的每一个内角都等于150°,
∴每个外角是30°,
∴多边形边数是360°÷30°=12,
则此多边形从一个顶点出发的对角线共有12-3=9条.
故选A.
5.解:该多边形的外角和为360°,
故内角和为2160°-360°=1800°,
故(n-2) 180°=1800°,
解得n=12.
故选:D.
6.解:五边形的内角和等于,,
,
、的平分线在五边形内相交于点,
,
.
故选:C.
7.解:设每一个外角都为x,则相邻的内角为4x,
由题意得,4x+x=180°,
解得:x=36°,
多边形的外角和为360°,
360°÷36°=10,
所以这个多边形的边数为10,
则该多边形的内角和是:(10﹣8)×180=1440°.
故选:C.
8.解:如图,
根据题意得: ,
∵ ,
∴.
故选:C
9.解:设此多边形的边数为n,由题意,有
(n﹣2) 180°=1440°,
解得n=10,即此多边形的边数为10.
故答案为:10.
10.解:正五方形的一个内角度数为,
∴需要的多边形的一个内角度数为,
∴需要的多边形的一个外角度数为,
∴第三个正多边形的边数为.
故答案为:10.
11.解:∵,
∴少加的内角是:.
故答案为:.
12.解:设多边形截去一个角的边数为,根据题意得:
又截去一个角后的多边形的边可以增加1、不变、减少1,
原多边形的边数为9或10或11.
13.解:,
.
故这个正多边形从一个顶点出发可以作的对角线条数是.
故答案为:.
14.解:如图:
∵多边形的外角和为,
∴,
∵,
∴;
故答案为:.
15.解:多边形内角和(为正整数),
当多边形边数增加2时,内角和增加,内角和不一定变为的2倍,故①正确,③错误;
边形外角和为,
当多边形边数增加2时,外角和不会增加,故②错误,④错误;
故答案为:①.
16.解:连接ED,
∵∠A+∠B=180°-∠AOB,∠BED+∠ADE=180°-∠DOE,∠AOB=∠DOE,
∴∠A+∠B=∠BED+∠ADE,
∵∠CDE+∠DEF+∠C+∠F+∠G=(5-2) ×180°=540°,
即∠CDO+∠ADE+BED+∠BEF+∠C+∠F+∠G=540°,
∴∠A+∠B+∠C+∠CDO+∠BEF+∠F+∠G=540°.
故答案为:540°.
17.解:设这个正多边的外角为x,则内角为5x﹣60°,
由题意得:x+5x﹣60=180,
解得:x=40,
360°÷40°=9.(9﹣2)×180°=1260°
答:这个正多边形的边数是9,内角和是1260°.
18.解:(1)设这个多边形的边数为n,
∵n边形的内角和为(n﹣2) 180°,多边形的外角和为360°,
∴(n﹣2) 180°=360°×3,
解得n=8.
∴这个多边形的边数为8.
(2)在△DFB中,
∵DF⊥AB,
∴∠FDB=90°,
∵∠F=40°,∠FDB+∠F+∠B=180°,
∴∠B=50°.
在△ABC中,
∵∠A=30°,∠B=50°,
∴∠ACF=30°+50°=80°.
19.解:选80cm×80cm的地板砖花费较少,理由如下:
客厅的面积为:
6.4×4.8=30.72﹙㎡﹚
第一种地砖的面积为:0.8×0.8=0.64﹙㎡﹚
所需要的块数与费用为:
30.72÷0.64×40=48×40=1920﹙元﹚
第二种地砖的面积为:0.6×0.6=0.36﹙㎡﹚
所需要的地砖块数与费用为:
30.72÷0.36×25≈86×25=2150﹙元﹚
第三种地砖的面积为:0.4×0.4=0.16﹙㎡﹚
所需要的地砖块数与费用为:
30.72÷0.16×15≈86×25=2880﹙元﹚
1920<2150<2880,
由此可知,应该选用规格为80×80的地砖铺贴.
20.(1)解:设多边形的边数为n,
由题意得:,
解得:,
∵n为整数,
∴多边形内角和为是不可能的;
(2)解:设应加的内角为x,多加的外角为y,
由题意得,,
∵,
∴,
∴,
∵n为整数,
∴或14,
∴佳佳求的是十三边形或十四边形的内角和.
(3)解:设那个外角的度数为m,与之相邻的内角度数为n,
∵十三边形的内角和:,
∴,
又∵,
∴.
∵十四边形的内角和:,
∴,
又∵,
∴.
∴那个外角的度数为或
21.解:(1)∵在四边形ABCD中,∠A与∠C互补,∴∠ABC+∠ADC=180°.
∵∠ABC、∠ADC的平分线分别与CD、AB相交于点E、F,∴∠ABE∠ABC,∠CDF∠ADC,而∠CDF=40°,∴∠ADC=2×40°=80°,∴2∠ABE+80°=180°,∴∠ABE=50°;
(2)DF与BE平行.理由如下:
∵在四边形ABCD中,∠A=∠C=90°,∴∠ABC+∠ADC=180°.
∵∠ABC、∠ADC的平分线分别与CD、AB相交于点E、F,∴∠ABE∠ABC,∠ADF∠ADC,∴∠ABE+∠ADF=90°,而∠AFD+∠ADF=90°,∴∠AFD=∠ABE,∴DF∥BE.
22.解:(1)∵DP、CP分别平分∠ADC和∠ACD,
∴∠PDC=∠ADC,∠PCD=∠ACD,
∴∠DPC=180°﹣∠PDC﹣∠PCD
=180°﹣∠ADC﹣∠ACD
=180°﹣(∠ADC+∠ACD)
=180°﹣(180°﹣∠A)
=90°+ ∠A,
∴如果∠A=90°,那么∠P=135°;如果∠A=x°,则∠P=(90+)°;
(2)∵DP、CP分别平分∠ADC和∠BCD,
∴∠PDC=∠ADC,∠PCD=∠BCD,
∴∠DPC=180°﹣∠PDC﹣∠PCD
=180°﹣∠ADC﹣∠BCD
=180°﹣(∠ADC+∠BCD)
=180°﹣(360°﹣∠A﹣∠B)
=(∠A+∠B);
(3)五边形ABCDEF的内角和为:(5﹣2) 180°=540°,
∵DP、CP分别平分∠EDC和∠BCD,
∴∠PDC=∠EDC,∠PCD=∠BCD,
∴∠P=180°﹣∠PDC﹣∠PCD
=180°﹣∠EDC﹣∠BCD
=180°﹣(∠EDC+∠BCD)
=180°﹣(540°﹣∠A﹣∠B﹣∠E)
=(∠A+∠B+∠E)﹣90°,
即∠P=(∠A+∠B+∠E)﹣90°;
(4)同(1)可得,∠P=(∠A3+∠A4+∠A5+…∠An)﹣(n﹣4)×90°.
故答案为(1)如果∠A=90°,那么∠P=135°;如果∠A=x°,则∠P=(90+)°(2)∠P=180°﹣∠PDC﹣∠PCD=(∠A+∠B)(3)∠P=(∠A+∠B+∠E)﹣90°(4)∠P=(∠A3+∠A4+∠A5+…∠An)﹣(n﹣4)×90°
同步自主提升训练题(附答案)
一、单选题
1.四边形的内角和与外角和的数量关系,正确的是( )
A.内角和比外角和大180° B.外角和比内角和大180°
C.内角和比外角和大360° D.内角和与外角和相等
2.正八边形每个内角度数为( )
A.120° B.135° C.150° D.160°
3.若一个多边形截去一个角后变成了六边形,则原来多边形的边数可能是( )
A.5或6 B.6或7 C.5或6或7 D.6或7或8
4.多边形每一个内角都等于150°,则从该多边形一个顶点出发,可引出对角线的条数为( )
A.9条 B.8条 C.7条 D.6条
5.已知一个多边形的内角和与外角和的和为2160°,这个多边形的边数为( )
A.9 B.10 C.11 D.12
6.如图,五边形中,,CP,DP分别平分,,则( )
A.60° B.72° C.70° D.78°
7.一多边形的每一个内角都等于它相邻外角的4倍,则该多边形的内角和是( )
A.360° B.900° C.1440° D.1800°
8.如图,( )度.
A.180 B.270 C.360 D.540
二、填空题
9.n边形的内角和为1440°,则n= .
10.用三个正多边形镶嵌,已知其中两个的边数均为5,则第三个正多边形的边数为 .
11.在计算某n边形的内角和时,不小心少算了一个内角,得到和为,这个角的大小是 .
12.一个多边形截去一个角后,形成的另一个多边形的内角和是1440°.则原来多边形的边数是 .
13.已知某正多边形每一个外角都等于,则从此多边形一个顶点出发,可以引的对角线的条数是 条
14.“花影遮墙,峰峦叠窗”,苏州园林空透的窗棂中蕴含着许多的数学元素.图①中的窗棂是冰裂纹窗棂,图②是这种窗棂中的部分图案.若,则 °.
15.将一个多边形的边数增加2,下列4个说法中,①内角和增加,②外角和增加360°,③内角和变为原来的2倍,④外角和变为原来的2倍;正确的有: .(填序号)
16.如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G= .
三、解答题
17.一个正多边形的每一个内角比每一个外角的5倍还小60°,求这个正多边形的边数及内角和.
18.(1)已知一个多边形的内角和是它的外角和的 3 倍,求这个多边形的边数.
(2)如图,点F 是△ABC 的边 BC 延长线上一点.DF⊥AB,∠A=30°,∠F=40°,求∠ACF 的度数.
19.小明家准备用正方形地板砖铺设客厅,客厅的长为6.4 m,宽为4.8 m.装修工人提出两种铺设方案:第一种方案是铺设80 cm×80 cm的地板砖,每块40元;第二种方案是铺设60 cm×60 cm的地板砖,每块25元;第三种方案是铺设40 cm×40 cm的地板砖,每块15元.你能从中帮他选一种材料的费用少且铺得又整齐的方案吗?
20.阅读佳佳与明明的对话,解决下列问题:
佳佳:我把一个多边形的各内角相加,所得的和为;
明明:什么?不可能的!虽然你的运算正确,但是你错把一个外角当成一个内角了!
(1)“多边形内角和为”,为什么不可能?
(2)佳佳求的是几边形的内角和?
(3)错当成内角的那个外角为多少度?
21.如图,在四边形ABCD中,∠ABC、∠ADC的平分线分别与CD、AB相交于点E、F.
(1)若∠A与∠C互补,∠CDF=40°,求∠ABE的度数.
(2)若∠A=∠C=90°,试判断DF与BE有怎样的位置关系,并请说明理由.
22.(1)已知:如图1,P为△ADC内一点,DP、CP分别平分∠ADC和∠ACD,如果∠A=90°,那么∠P=______°;如果∠A=x°,则∠P=____________°;(答案直接填在题中横线上)
(2)如图2,P为四边形ABCD内一点,DP、CP分别平分∠ADC和∠BCD,试探究∠P与∠A+∠B的数量关系,并写出你的探索过程;
(3)如图3,P为五边形ABCDE内一点,DP、CP分别平分∠EDC和∠BCD,请直接写出∠P与∠A+∠B+∠E的数量关系:________________;
(4)若P为n边形A1A2A3…An内一点,PA1平分∠AnA1A2,PA2平分∠A1A2A3,请直接写出∠P与∠A3+A4+A5+…∠An的数量关系:__________________________.(用含n的代数式表示)
参考答案
1.解:A.四边形的内角和与外角和相等,都等于360°,故本选项表述错误;
B.四边形的内角和与外角和相等,都等于360°,故本选项表述错误;
C.六四边形的内角和与外角和相等,都等于360°,故本选项表述错误;
D.四边形的内角和与外角和相等,都等于360°,故本选项表述正确.
故选:D.
2.解:∵正多边形的每一个内角相等,则对应的外角也相等,
一个外角等于:
∴内角为
故选B
3.解:如图,原来多边形的边数可能是5,6,7.
故选C
4.解:∵多边形的每一个内角都等于150°,
∴每个外角是30°,
∴多边形边数是360°÷30°=12,
则此多边形从一个顶点出发的对角线共有12-3=9条.
故选A.
5.解:该多边形的外角和为360°,
故内角和为2160°-360°=1800°,
故(n-2) 180°=1800°,
解得n=12.
故选:D.
6.解:五边形的内角和等于,,
,
、的平分线在五边形内相交于点,
,
.
故选:C.
7.解:设每一个外角都为x,则相邻的内角为4x,
由题意得,4x+x=180°,
解得:x=36°,
多边形的外角和为360°,
360°÷36°=10,
所以这个多边形的边数为10,
则该多边形的内角和是:(10﹣8)×180=1440°.
故选:C.
8.解:如图,
根据题意得: ,
∵ ,
∴.
故选:C
9.解:设此多边形的边数为n,由题意,有
(n﹣2) 180°=1440°,
解得n=10,即此多边形的边数为10.
故答案为:10.
10.解:正五方形的一个内角度数为,
∴需要的多边形的一个内角度数为,
∴需要的多边形的一个外角度数为,
∴第三个正多边形的边数为.
故答案为:10.
11.解:∵,
∴少加的内角是:.
故答案为:.
12.解:设多边形截去一个角的边数为,根据题意得:
又截去一个角后的多边形的边可以增加1、不变、减少1,
原多边形的边数为9或10或11.
13.解:,
.
故这个正多边形从一个顶点出发可以作的对角线条数是.
故答案为:.
14.解:如图:
∵多边形的外角和为,
∴,
∵,
∴;
故答案为:.
15.解:多边形内角和(为正整数),
当多边形边数增加2时,内角和增加,内角和不一定变为的2倍,故①正确,③错误;
边形外角和为,
当多边形边数增加2时,外角和不会增加,故②错误,④错误;
故答案为:①.
16.解:连接ED,
∵∠A+∠B=180°-∠AOB,∠BED+∠ADE=180°-∠DOE,∠AOB=∠DOE,
∴∠A+∠B=∠BED+∠ADE,
∵∠CDE+∠DEF+∠C+∠F+∠G=(5-2) ×180°=540°,
即∠CDO+∠ADE+BED+∠BEF+∠C+∠F+∠G=540°,
∴∠A+∠B+∠C+∠CDO+∠BEF+∠F+∠G=540°.
故答案为:540°.
17.解:设这个正多边的外角为x,则内角为5x﹣60°,
由题意得:x+5x﹣60=180,
解得:x=40,
360°÷40°=9.(9﹣2)×180°=1260°
答:这个正多边形的边数是9,内角和是1260°.
18.解:(1)设这个多边形的边数为n,
∵n边形的内角和为(n﹣2) 180°,多边形的外角和为360°,
∴(n﹣2) 180°=360°×3,
解得n=8.
∴这个多边形的边数为8.
(2)在△DFB中,
∵DF⊥AB,
∴∠FDB=90°,
∵∠F=40°,∠FDB+∠F+∠B=180°,
∴∠B=50°.
在△ABC中,
∵∠A=30°,∠B=50°,
∴∠ACF=30°+50°=80°.
19.解:选80cm×80cm的地板砖花费较少,理由如下:
客厅的面积为:
6.4×4.8=30.72﹙㎡﹚
第一种地砖的面积为:0.8×0.8=0.64﹙㎡﹚
所需要的块数与费用为:
30.72÷0.64×40=48×40=1920﹙元﹚
第二种地砖的面积为:0.6×0.6=0.36﹙㎡﹚
所需要的地砖块数与费用为:
30.72÷0.36×25≈86×25=2150﹙元﹚
第三种地砖的面积为:0.4×0.4=0.16﹙㎡﹚
所需要的地砖块数与费用为:
30.72÷0.16×15≈86×25=2880﹙元﹚
1920<2150<2880,
由此可知,应该选用规格为80×80的地砖铺贴.
20.(1)解:设多边形的边数为n,
由题意得:,
解得:,
∵n为整数,
∴多边形内角和为是不可能的;
(2)解:设应加的内角为x,多加的外角为y,
由题意得,,
∵,
∴,
∴,
∵n为整数,
∴或14,
∴佳佳求的是十三边形或十四边形的内角和.
(3)解:设那个外角的度数为m,与之相邻的内角度数为n,
∵十三边形的内角和:,
∴,
又∵,
∴.
∵十四边形的内角和:,
∴,
又∵,
∴.
∴那个外角的度数为或
21.解:(1)∵在四边形ABCD中,∠A与∠C互补,∴∠ABC+∠ADC=180°.
∵∠ABC、∠ADC的平分线分别与CD、AB相交于点E、F,∴∠ABE∠ABC,∠CDF∠ADC,而∠CDF=40°,∴∠ADC=2×40°=80°,∴2∠ABE+80°=180°,∴∠ABE=50°;
(2)DF与BE平行.理由如下:
∵在四边形ABCD中,∠A=∠C=90°,∴∠ABC+∠ADC=180°.
∵∠ABC、∠ADC的平分线分别与CD、AB相交于点E、F,∴∠ABE∠ABC,∠ADF∠ADC,∴∠ABE+∠ADF=90°,而∠AFD+∠ADF=90°,∴∠AFD=∠ABE,∴DF∥BE.
22.解:(1)∵DP、CP分别平分∠ADC和∠ACD,
∴∠PDC=∠ADC,∠PCD=∠ACD,
∴∠DPC=180°﹣∠PDC﹣∠PCD
=180°﹣∠ADC﹣∠ACD
=180°﹣(∠ADC+∠ACD)
=180°﹣(180°﹣∠A)
=90°+ ∠A,
∴如果∠A=90°,那么∠P=135°;如果∠A=x°,则∠P=(90+)°;
(2)∵DP、CP分别平分∠ADC和∠BCD,
∴∠PDC=∠ADC,∠PCD=∠BCD,
∴∠DPC=180°﹣∠PDC﹣∠PCD
=180°﹣∠ADC﹣∠BCD
=180°﹣(∠ADC+∠BCD)
=180°﹣(360°﹣∠A﹣∠B)
=(∠A+∠B);
(3)五边形ABCDEF的内角和为:(5﹣2) 180°=540°,
∵DP、CP分别平分∠EDC和∠BCD,
∴∠PDC=∠EDC,∠PCD=∠BCD,
∴∠P=180°﹣∠PDC﹣∠PCD
=180°﹣∠EDC﹣∠BCD
=180°﹣(∠EDC+∠BCD)
=180°﹣(540°﹣∠A﹣∠B﹣∠E)
=(∠A+∠B+∠E)﹣90°,
即∠P=(∠A+∠B+∠E)﹣90°;
(4)同(1)可得,∠P=(∠A3+∠A4+∠A5+…∠An)﹣(n﹣4)×90°.
故答案为(1)如果∠A=90°,那么∠P=135°;如果∠A=x°,则∠P=(90+)°(2)∠P=180°﹣∠PDC﹣∠PCD=(∠A+∠B)(3)∠P=(∠A+∠B+∠E)﹣90°(4)∠P=(∠A3+∠A4+∠A5+…∠An)﹣(n﹣4)×90°
