人教版高中数学选择性必修第三册6.1分类加法计数原理与分步乘法计数原理(2) A组基础同步训练(含解析)
文档属性
| 名称 | 人教版高中数学选择性必修第三册6.1分类加法计数原理与分步乘法计数原理(2) A组基础同步训练(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 176.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-12 21:28:49 | ||
图片预览




文档简介
成套的课件成套的教案成套的试题尽在高中数学同步资源大全QQ群483122854
人教版高中数学选择性必修第三册
6.1分类加法计数原理与分步乘法计数原理(2)A组基础同步训练(原卷版)
一、选择题
1.求是中学的教学楼共有5层,每层均有两个楼梯,某同学从一楼上到五楼可能的走法有( )
A.10种 B.16种 C.25种 D.32种
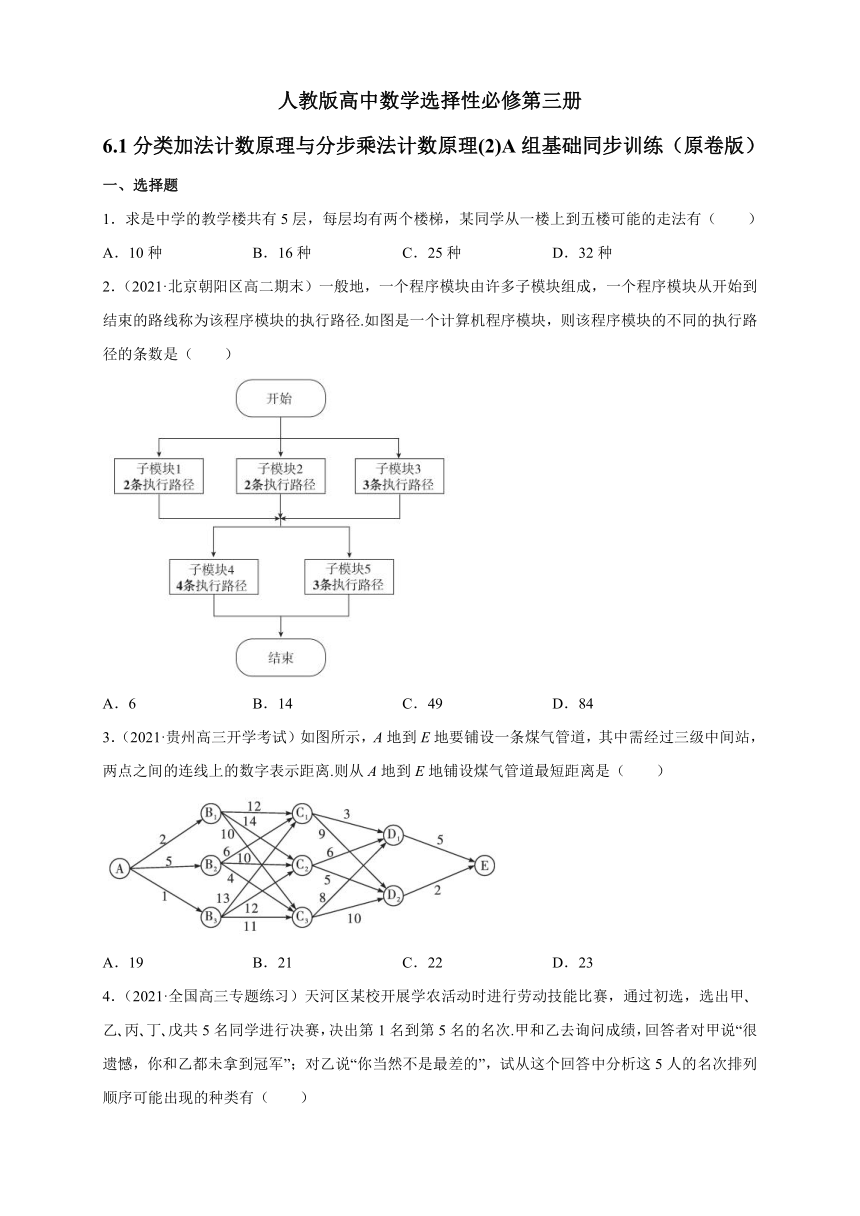
2.(2021·北京朝阳区高二期末)一般地,一个程序模块由许多子模块组成,一个程序模块从开始到结束的路线称为该程序模块的执行路径.如图是一个计算机程序模块,则该程序模块的不同的执行路径的条数是( )
A.6 B.14 C.49 D.84
3.(2021·贵州高三开学考试)如图所示,A地到E地要铺设一条煤气管道,其中需经过三级中间站,两点之间的连线上的数字表示距离.则从A地到E地铺设煤气管道最短距离是( )
A.19 B.21 C.22 D.23
4.(2021·全国高三专题练习)天河区某校开展学农活动时进行劳动技能比赛,通过初选,选出甲 乙 丙 丁 戊共5名同学进行决赛,决出第1名到第5名的名次.甲和乙去询问成绩,回答者对甲说“很遗憾,你和乙都未拿到冠军”;对乙说“你当然不是最差的”,试从这个回答中分析这5人的名次排列顺序可能出现的种类有( )
A.54种 B.60种 C.72种 D.96种
5.(2021·湖北黄石市黄石二中高二期末)过三棱柱中任意两个顶点连线作直线,在所有这些直线连线中构成异面直线的对数为( )
A.18 B.30 C.36 D.54
6.(多选题)(2021·江苏苏州中学高二月考)现安排高二年级A,B,C三名同学到甲、乙、丙、丁四个工厂进行社会实践,每名同学只能选择一个工),且允许多人选择同一个工厂,则下列说法正确的是( )
A.所有可能的方法有种
B.若工厂甲必须有同学去,则不同的安排方法有37种
C.若同学A必须去工厂甲,则不同的安排方法有16种
D.若三名同学所选工厂各不相同,则不同的安排方法有24种
二、填空题
7. 3科老师都布置了作业,在同一时刻4名学生都做作业的可能情况有_______种.
8.(2021·全国高二课时练)假设今天是4月23日,某市未来六天的空气质量预报情况如图所示.该市有甲、乙、丙三人计划在未来六天(4月24日~4月29日)内选择一天出游,甲只选择空气质量为优的一天出游,乙不选择周一出游,丙不选择明天出游,且甲与乙不选择同一天出游,则这三人出游的不同方法数为________.
未来空气质量预报
明天 后天 周日 周一 周二 周三
4月24日 4月25日 4月26日 4月27日 4月28日 4月29日
优 优 优 优 良 良
9.(2021·广东深圳外国语学校高二期末)回文联是我国对联中的一种.用回文形式写成的对联,既可顺读,也可倒读,不仅意思不变,而且颇具趣味.相传,清代北京城里有一家饭馆叫“天然居”,曾有一副有名的回文联:“客上天然居,居然天上客;人过大佛寺,寺佛大过人.”在数学中也有这样一类顺读与倒读都是同一个数的自然数,称之为:“回文数”.如44,585,2662 等,那么用数字1,2,3, 4,5,6可以组成4位“回文数”的个数为_______.
10.(2021·湖北高三期中)5400的正约数有______个
三、解答题
11.现某学校共有34人自愿组成数学建模社团,其中高一年级13人,高二年级12人,高三年级9人.
(1)选其中一人为负责人,共有多少种不同的选法?
(2)每个年级选一名组长,有多少种不同的选法?
(3)选两人作为社团发言人,这两人需要来自不同的年级,有多少种不同的选法?
12.(2021·四川省眉山高二期末)数学上的“四色问题”,是指“任何一张地图只用四种颜色就能使具有公共边界的国家着上不同的颜色。”,现有五种颜色供选择,涂色我国西部五省,要求每省涂一色,相邻各省不同色,有多少种涂色方法.
人教版高中数学选择性必修第三册
6.1分类加法计数原理与分步乘法计数原理(2)A组基础同步训练(解析版)
一、选择题
1.求是中学的教学楼共有5层,每层均有两个楼梯,某同学从一楼上到五楼可能的走法有( )
A.10种 B.16种 C.25种 D.32种
【答案】B
【详解】走法共分四步:一层到二层2种,二层到三层2种,三层到四层2种,四层到五层2种,一共种.
2.(2021·北京朝阳区高二期末)一般地,一个程序模块由许多子模块组成,一个程序模块从开始到结束的路线称为该程序模块的执行路径.如图是一个计算机程序模块,则该程序模块的不同的执行路径的条数是( )
A.6 B.14 C.49 D.84
【答案】C
【详解】由分类加法计数原理,子模块1或子模块2或子模块3的子路径共有条;
子模块4或子模块5中的子路径共有条,由分步乘法计数原理,整个模块的不同执行路径共有条,故选:C
3.(2021·贵州高三开学考试)如图所示,A地到E地要铺设一条煤气管道,其中需经过三级中间站,两点之间的连线上的数字表示距离.则从A地到E地铺设煤气管道最短距离是( )
A.19 B.21 C.22 D.23
【答案】A
【详解】对各个路线进行计算可得,由到到到到,距离共19为最短距离.
4.(2021·全国高三专题练习)天河区某校开展学农活动时进行劳动技能比赛,通过初选,选出甲 乙 丙 丁 戊共5名同学进行决赛,决出第1名到第5名的名次.甲和乙去询问成绩,回答者对甲说“很遗憾,你和乙都未拿到冠军”;对乙说“你当然不是最差的”,试从这个回答中分析这5人的名次排列顺序可能出现的种类有( )
A.54种 B.60种 C.72种 D.96种
【答案】A
【详解】由题意,甲乙不是第一名且乙不是最后一名,乙的限制最多,故先排乙,有3种情况,再排甲,也有3种情况,余下3人有种情况,利用分步相乘计数原理知有种情况,故选:A.
5.(2021·湖北黄石市黄石二中高二期末)过三棱柱中任意两个顶点连线作直线,在所有这些直线连线中构成异面直线的对数为( )
A.18 B.30 C.36 D.54
【答案】C
【详解】解:如图,分以下几类:
棱柱侧棱与底面边之间所构成的异面直线有:对;
棱柱侧棱与侧面对角线之间所构成的异面直线有:对;
底面边与侧面对角线之间所构成的异面直线有:对;
底面边与底面边之间所构成的异面直线有:对;
侧面对角线与侧面对角线之间所构成的异面直线有:对;
所以共有对.故选:C.
6.(多选题)(2021·江苏苏州中学高二月考)现安排高二年级A,B,C三名同学到甲、乙、丙、丁四个工厂进行社会实践,每名同学只能选择一个工),且允许多人选择同一个工厂,则下列说法正确的是( )
A.所有可能的方法有种
B.若工厂甲必须有同学去,则不同的安排方法有37种
C.若同学A必须去工厂甲,则不同的安排方法有16种
D.若三名同学所选工厂各不相同,则不同的安排方法有24种
【答案】BCD
【详解】所有可能的方法有种,A错误.对于B,分三种情况:第一种:若有1名同学去工厂甲,则去工厂甲的同学情况为3种,另外两名同学的安排方法有种,此种情况共有种,第二种:若有两名同学去工厂甲,则同学选派情况有3种,另外一名同学的排法有3种,此种情况共有种,第三种情况,若三名同学都去工甲,此种情况唯一,则共有种安排方法,B正确.对于C,若A必去甲工厂,则B,C两名同学各有4种安排,共有种安排,C正确.对于D,若三名同学所选工厂各不同,则共有种安排,D正确.
二、填空题
7. 3科老师都布置了作业,在同一时刻4名学生都做作业的可能情况有_______种.
【答案】81
【详解】因为3科老师都布置了作业,在同一时刻每个学生做作业的情况有3种可能,
所以4名学生都做作业的可能情况3×3×3×3=81种.
8.(2021·全国高二课时练)假设今天是4月23日,某市未来六天的空气质量预报情况如图所示.该市有甲、乙、丙三人计划在未来六天(4月24日~4月29日)内选择一天出游,甲只选择空气质量为优的一天出游,乙不选择周一出游,丙不选择明天出游,且甲与乙不选择同一天出游,则这三人出游的不同方法数为________.
未来空气质量预报
明天 后天 周日 周一 周二 周三
4月24日 4月25日 4月26日 4月27日 4月28日 4月29日
优 优 优 优 良 良
【答案】85
【详解】若甲选择周一出游,则三人出游的不同方法数;
若甲不选择周一出游,则三人出游的不同方法数.
故这三人出游的不同方法数.
9.(2021·广东深圳外国语学校高二期末)回文联是我国对联中的一种.用回文形式写成的对联,既可顺读,也可倒读,不仅意思不变,而且颇具趣味.相传,清代北京城里有一家饭馆叫“天然居”,曾有一副有名的回文联:“客上天然居,居然天上客;人过大佛寺,寺佛大过人.”在数学中也有这样一类顺读与倒读都是同一个数的自然数,称之为:“回文数”.如44,585,2662 等,那么用数字1,2,3, 4,5,6可以组成4位“回文数”的个数为_______.
【答案】
【详解】根据题意,分2种情况讨论:
①4位“回文数”中数字全部相同,有6种情况,即此时有6个4位“回文数”;
②4位“回文数”中有2个不同的数字,有种情况,即此时有30个4位“回文数”;
则一共有个4位“回文数”.
10.(2021·湖北高三期中)5400的正约数有______个
【答案】48
【详解】,5400的正约数一定是由2的幂与3的幂和5的幂相乘的结果,
所以正约数个数为.
三、解答题
11.现某学校共有34人自愿组成数学建模社团,其中高一年级13人,高二年级12人,高三年级9人.
(1)选其中一人为负责人,共有多少种不同的选法?
(2)每个年级选一名组长,有多少种不同的选法?
(3)选两人作为社团发言人,这两人需要来自不同的年级,有多少种不同的选法?
【详解】(1)根据题意,选其中一人为负责人,有3种情况,
若选出的是高一学生,有13种情况,
若选出的是高二学生,有12种情况,
若选出的是高三学生,有9种情况,
由分类计数原理可得,共有12+13+9=34种选法.
(2)根据题意,从高一学生中选出1人,有13种情况;
从高二学生中选出1人,有12种情况;
从高三学生中选出1人,有9种情况;
由分步计数原理,可得共有12×13×9=1404种选法.
(3)根据题意,分三种情况讨论:
若选出的是高一、高二学生,有12×13=156种情况,
若选出的是高一、高三学生,有13×9=117种情况,
若选出的是高二、高三学生,有12×9=108种情况,
由分类计数原理可得,共有156+117+108=381种选法.
12.(2021·四川省眉山高二期末)数学上的“四色问题”,是指“任何一张地图只用四种颜色就能使具有公共边界的国家着上不同的颜色。”,现有五种颜色供选择,涂色我国西部五省,要求每省涂一色,相邻各省不同色,有多少种涂色方法.
【详解】对于新疆有5种涂色的方法,
对于青海有4种涂色方法,
对于西藏有3种涂色方法,
对于四川:若与新疆颜色相同,则有1种涂色方法,此时甘肃有3种涂色方法;
若四川与新疆颜色不相同,则四川只有2种涂色方法,此时甘肃有2种涂色方法;
根据分步、分类计数原理,则共有5×4×3×(2×2+1×3)=420种方法.
联系QQ309000116加入百度网盘群3500G一线老师必备资料一键转存,自动更新,一劳永逸
人教版高中数学选择性必修第三册
6.1分类加法计数原理与分步乘法计数原理(2)A组基础同步训练(原卷版)
一、选择题
1.求是中学的教学楼共有5层,每层均有两个楼梯,某同学从一楼上到五楼可能的走法有( )
A.10种 B.16种 C.25种 D.32种
2.(2021·北京朝阳区高二期末)一般地,一个程序模块由许多子模块组成,一个程序模块从开始到结束的路线称为该程序模块的执行路径.如图是一个计算机程序模块,则该程序模块的不同的执行路径的条数是( )
A.6 B.14 C.49 D.84
3.(2021·贵州高三开学考试)如图所示,A地到E地要铺设一条煤气管道,其中需经过三级中间站,两点之间的连线上的数字表示距离.则从A地到E地铺设煤气管道最短距离是( )
A.19 B.21 C.22 D.23
4.(2021·全国高三专题练习)天河区某校开展学农活动时进行劳动技能比赛,通过初选,选出甲 乙 丙 丁 戊共5名同学进行决赛,决出第1名到第5名的名次.甲和乙去询问成绩,回答者对甲说“很遗憾,你和乙都未拿到冠军”;对乙说“你当然不是最差的”,试从这个回答中分析这5人的名次排列顺序可能出现的种类有( )
A.54种 B.60种 C.72种 D.96种
5.(2021·湖北黄石市黄石二中高二期末)过三棱柱中任意两个顶点连线作直线,在所有这些直线连线中构成异面直线的对数为( )
A.18 B.30 C.36 D.54
6.(多选题)(2021·江苏苏州中学高二月考)现安排高二年级A,B,C三名同学到甲、乙、丙、丁四个工厂进行社会实践,每名同学只能选择一个工),且允许多人选择同一个工厂,则下列说法正确的是( )
A.所有可能的方法有种
B.若工厂甲必须有同学去,则不同的安排方法有37种
C.若同学A必须去工厂甲,则不同的安排方法有16种
D.若三名同学所选工厂各不相同,则不同的安排方法有24种
二、填空题
7. 3科老师都布置了作业,在同一时刻4名学生都做作业的可能情况有_______种.
8.(2021·全国高二课时练)假设今天是4月23日,某市未来六天的空气质量预报情况如图所示.该市有甲、乙、丙三人计划在未来六天(4月24日~4月29日)内选择一天出游,甲只选择空气质量为优的一天出游,乙不选择周一出游,丙不选择明天出游,且甲与乙不选择同一天出游,则这三人出游的不同方法数为________.
未来空气质量预报
明天 后天 周日 周一 周二 周三
4月24日 4月25日 4月26日 4月27日 4月28日 4月29日
优 优 优 优 良 良
9.(2021·广东深圳外国语学校高二期末)回文联是我国对联中的一种.用回文形式写成的对联,既可顺读,也可倒读,不仅意思不变,而且颇具趣味.相传,清代北京城里有一家饭馆叫“天然居”,曾有一副有名的回文联:“客上天然居,居然天上客;人过大佛寺,寺佛大过人.”在数学中也有这样一类顺读与倒读都是同一个数的自然数,称之为:“回文数”.如44,585,2662 等,那么用数字1,2,3, 4,5,6可以组成4位“回文数”的个数为_______.
10.(2021·湖北高三期中)5400的正约数有______个
三、解答题
11.现某学校共有34人自愿组成数学建模社团,其中高一年级13人,高二年级12人,高三年级9人.
(1)选其中一人为负责人,共有多少种不同的选法?
(2)每个年级选一名组长,有多少种不同的选法?
(3)选两人作为社团发言人,这两人需要来自不同的年级,有多少种不同的选法?
12.(2021·四川省眉山高二期末)数学上的“四色问题”,是指“任何一张地图只用四种颜色就能使具有公共边界的国家着上不同的颜色。”,现有五种颜色供选择,涂色我国西部五省,要求每省涂一色,相邻各省不同色,有多少种涂色方法.
人教版高中数学选择性必修第三册
6.1分类加法计数原理与分步乘法计数原理(2)A组基础同步训练(解析版)
一、选择题
1.求是中学的教学楼共有5层,每层均有两个楼梯,某同学从一楼上到五楼可能的走法有( )
A.10种 B.16种 C.25种 D.32种
【答案】B
【详解】走法共分四步:一层到二层2种,二层到三层2种,三层到四层2种,四层到五层2种,一共种.
2.(2021·北京朝阳区高二期末)一般地,一个程序模块由许多子模块组成,一个程序模块从开始到结束的路线称为该程序模块的执行路径.如图是一个计算机程序模块,则该程序模块的不同的执行路径的条数是( )
A.6 B.14 C.49 D.84
【答案】C
【详解】由分类加法计数原理,子模块1或子模块2或子模块3的子路径共有条;
子模块4或子模块5中的子路径共有条,由分步乘法计数原理,整个模块的不同执行路径共有条,故选:C
3.(2021·贵州高三开学考试)如图所示,A地到E地要铺设一条煤气管道,其中需经过三级中间站,两点之间的连线上的数字表示距离.则从A地到E地铺设煤气管道最短距离是( )
A.19 B.21 C.22 D.23
【答案】A
【详解】对各个路线进行计算可得,由到到到到,距离共19为最短距离.
4.(2021·全国高三专题练习)天河区某校开展学农活动时进行劳动技能比赛,通过初选,选出甲 乙 丙 丁 戊共5名同学进行决赛,决出第1名到第5名的名次.甲和乙去询问成绩,回答者对甲说“很遗憾,你和乙都未拿到冠军”;对乙说“你当然不是最差的”,试从这个回答中分析这5人的名次排列顺序可能出现的种类有( )
A.54种 B.60种 C.72种 D.96种
【答案】A
【详解】由题意,甲乙不是第一名且乙不是最后一名,乙的限制最多,故先排乙,有3种情况,再排甲,也有3种情况,余下3人有种情况,利用分步相乘计数原理知有种情况,故选:A.
5.(2021·湖北黄石市黄石二中高二期末)过三棱柱中任意两个顶点连线作直线,在所有这些直线连线中构成异面直线的对数为( )
A.18 B.30 C.36 D.54
【答案】C
【详解】解:如图,分以下几类:
棱柱侧棱与底面边之间所构成的异面直线有:对;
棱柱侧棱与侧面对角线之间所构成的异面直线有:对;
底面边与侧面对角线之间所构成的异面直线有:对;
底面边与底面边之间所构成的异面直线有:对;
侧面对角线与侧面对角线之间所构成的异面直线有:对;
所以共有对.故选:C.
6.(多选题)(2021·江苏苏州中学高二月考)现安排高二年级A,B,C三名同学到甲、乙、丙、丁四个工厂进行社会实践,每名同学只能选择一个工),且允许多人选择同一个工厂,则下列说法正确的是( )
A.所有可能的方法有种
B.若工厂甲必须有同学去,则不同的安排方法有37种
C.若同学A必须去工厂甲,则不同的安排方法有16种
D.若三名同学所选工厂各不相同,则不同的安排方法有24种
【答案】BCD
【详解】所有可能的方法有种,A错误.对于B,分三种情况:第一种:若有1名同学去工厂甲,则去工厂甲的同学情况为3种,另外两名同学的安排方法有种,此种情况共有种,第二种:若有两名同学去工厂甲,则同学选派情况有3种,另外一名同学的排法有3种,此种情况共有种,第三种情况,若三名同学都去工甲,此种情况唯一,则共有种安排方法,B正确.对于C,若A必去甲工厂,则B,C两名同学各有4种安排,共有种安排,C正确.对于D,若三名同学所选工厂各不同,则共有种安排,D正确.
二、填空题
7. 3科老师都布置了作业,在同一时刻4名学生都做作业的可能情况有_______种.
【答案】81
【详解】因为3科老师都布置了作业,在同一时刻每个学生做作业的情况有3种可能,
所以4名学生都做作业的可能情况3×3×3×3=81种.
8.(2021·全国高二课时练)假设今天是4月23日,某市未来六天的空气质量预报情况如图所示.该市有甲、乙、丙三人计划在未来六天(4月24日~4月29日)内选择一天出游,甲只选择空气质量为优的一天出游,乙不选择周一出游,丙不选择明天出游,且甲与乙不选择同一天出游,则这三人出游的不同方法数为________.
未来空气质量预报
明天 后天 周日 周一 周二 周三
4月24日 4月25日 4月26日 4月27日 4月28日 4月29日
优 优 优 优 良 良
【答案】85
【详解】若甲选择周一出游,则三人出游的不同方法数;
若甲不选择周一出游,则三人出游的不同方法数.
故这三人出游的不同方法数.
9.(2021·广东深圳外国语学校高二期末)回文联是我国对联中的一种.用回文形式写成的对联,既可顺读,也可倒读,不仅意思不变,而且颇具趣味.相传,清代北京城里有一家饭馆叫“天然居”,曾有一副有名的回文联:“客上天然居,居然天上客;人过大佛寺,寺佛大过人.”在数学中也有这样一类顺读与倒读都是同一个数的自然数,称之为:“回文数”.如44,585,2662 等,那么用数字1,2,3, 4,5,6可以组成4位“回文数”的个数为_______.
【答案】
【详解】根据题意,分2种情况讨论:
①4位“回文数”中数字全部相同,有6种情况,即此时有6个4位“回文数”;
②4位“回文数”中有2个不同的数字,有种情况,即此时有30个4位“回文数”;
则一共有个4位“回文数”.
10.(2021·湖北高三期中)5400的正约数有______个
【答案】48
【详解】,5400的正约数一定是由2的幂与3的幂和5的幂相乘的结果,
所以正约数个数为.
三、解答题
11.现某学校共有34人自愿组成数学建模社团,其中高一年级13人,高二年级12人,高三年级9人.
(1)选其中一人为负责人,共有多少种不同的选法?
(2)每个年级选一名组长,有多少种不同的选法?
(3)选两人作为社团发言人,这两人需要来自不同的年级,有多少种不同的选法?
【详解】(1)根据题意,选其中一人为负责人,有3种情况,
若选出的是高一学生,有13种情况,
若选出的是高二学生,有12种情况,
若选出的是高三学生,有9种情况,
由分类计数原理可得,共有12+13+9=34种选法.
(2)根据题意,从高一学生中选出1人,有13种情况;
从高二学生中选出1人,有12种情况;
从高三学生中选出1人,有9种情况;
由分步计数原理,可得共有12×13×9=1404种选法.
(3)根据题意,分三种情况讨论:
若选出的是高一、高二学生,有12×13=156种情况,
若选出的是高一、高三学生,有13×9=117种情况,
若选出的是高二、高三学生,有12×9=108种情况,
由分类计数原理可得,共有156+117+108=381种选法.
12.(2021·四川省眉山高二期末)数学上的“四色问题”,是指“任何一张地图只用四种颜色就能使具有公共边界的国家着上不同的颜色。”,现有五种颜色供选择,涂色我国西部五省,要求每省涂一色,相邻各省不同色,有多少种涂色方法.
【详解】对于新疆有5种涂色的方法,
对于青海有4种涂色方法,
对于西藏有3种涂色方法,
对于四川:若与新疆颜色相同,则有1种涂色方法,此时甘肃有3种涂色方法;
若四川与新疆颜色不相同,则四川只有2种涂色方法,此时甘肃有2种涂色方法;
根据分步、分类计数原理,则共有5×4×3×(2×2+1×3)=420种方法.
联系QQ309000116加入百度网盘群3500G一线老师必备资料一键转存,自动更新,一劳永逸
