2024年中考备考专题讲义:函数应用题模型—建立函数模型解决实际问题 数学解题模型与方法(含解析)
文档属性
| 名称 | 2024年中考备考专题讲义:函数应用题模型—建立函数模型解决实际问题 数学解题模型与方法(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 705.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-14 15:07:35 | ||
图片预览




文档简介
应用题模型—建立函数模型解决实际问题 数学解题模型与方法
【解题模型与方法】
1、解决函数应用问题的基本思路方法
从终极目标量开始,建立与之相关的等量关系,可能会引出新的目标量,此时又以建立与新目标量相关的等量关系,...,.如此不断建立与新目标量相关的等量关系,直至最后一个等量关系中出现的量均为题设中的已知量与所设出的量为止.按照此法,通过不断的寻求该目标量的等量关系,可以逐步把题目中的各种信息、条件融合在目标量之下,进而将题目所涉及的量的关系程序化,从而构建数学模型,达到解决问题的目的.
2、用函数构建数学模型解决实际问题的步骤
(1)观察实际情景:对实际问题中的变化过程进行分析;
(2)发现和提出问题:析出常量、变量及其相互关系;
(3)收集数据、分析数据:明确其运动变化的基本特征,从而确定它的运动变化类型;
(4)选择函数模型:根据分析结果,选择适当的函数类型构建数学模型,将实际问题
化归为数学问题;
(5)求解函数模型:通过运算推理,求解函数模型;
(6)检验模型:利用函 数模型的解说明实际问题的变化规律,达到解决问题的目的.
【典型例题】
例题1.如图,在Rt△ABC中,∠C=90°,AC=3厘米,CB=4厘米.两个动点P,Q分别从A,C两点同时按顺时针方向沿△ABC的边运动.当点Q运动到点A时,P,Q两点运动即停止.点P,Q的运动速度分别为1厘米/秒、2厘米/秒,设点P运动的时间为t(秒).记线段PQ与从点P按顺时针方向沿△ABC的边到点Q的折线段所围成的图形的面积为S(平方厘米).
(1)用含t的代数式表示PC的长;
(2)当点P,Q运动时,求S与时间t的函数关系式,并写出自变量t的取值范围;
(3)点P,Q在运动的过程中,S有最大值吗?若有,请求出最大值;若没有,请说明理由.
解:(1)∵Rt△ABC中,∠C=90°,AC=3厘米,CB=4厘米,
∴AB=5厘米.
∵(4+5)÷2=秒.
∴P运动的最大距离为=厘米,
∴当点P在AC边上运动时,PC=3﹣t;
当点P在CB边上运动时,PC=t﹣3.
(2)当0<t≤2时,点P在AC边上,点Q在CB边上,如图所示,
∵AC=3,BC=4,AB=5,点P,Q的运动速度分别为1厘米/秒、2厘米/秒,
∴AP=1,CP=3﹣t,CQ=2t,
∵∠C=90°,
∴以P,C,Q三点为顶点的三角形是直角三角形.
S=S△PCQ=CP CQ=(3﹣t)×2t=﹣t2+3t,
当2<1≤3时,点P在AC边上,点Q在AB边上,如图所示,
∵AC=3,BC=4,AB=5,点P,Q的运动速度分别为1厘米/秒、2厘米/秒,
∴AP=t,AQ=9﹣2t,
∴线段PQ与从点P按顺时针方向沿△ABC的边到点Q的折线段所围成的图形为四边形PCBO.
此时S=S△CAB﹣S△APQ,过点P作PD⊥AQ于D.
∵∠A=∠A,∠ADP=∠ACB.
∴△ADP∽△ACB,
∴,即 ,解得 .
∴S△APQ===,
∴S=S△CAB﹣S△NPQ=﹣()=.
当 时,点P在CB边上,点Q在AB边上,如图所示.
由题知,AC=3,BC=4,AB=5,CP=t﹣3,BP=7﹣t,BQ=2t﹣4,
∴线段PQ与从点P按顺时针方向沿△ABC的边到点Q的折线段所围成的图形为三角形PQB.
此时,S=S△QPB,过点P作 PE⊥QB 于E.
∵∠B=∠B,∠BEP=∠BCA,
∴△BEP∽△BCA,
∴,即
解得 ,
∴.
综上,,
(3)由(2)知:,当0<t≤2时,,
当 时,S有最大值为 ;
当2<t≤3时,.
∵,当 时,函数值S随自变量t的增大而增大,
∴当t=3时,S有最大值为 ;
当 时,.
当 ,S有最大值为 ,
综上,当 时,S有最大值为 .
常考经典试题同步检测
考试范围:应用题;考试时间:100分钟;
一.选择题(共8小题)
1.小明学习了物理中的欧姆定律发现:电阻两端的电压=电流强度×电流通过的电阻.已知某滑动变阻器两端电压恒定,当变阻器的电阻调节为10Ω时,测得通过该变阻器的电流为24A,则通过该滑动变阻器的电流I(单位:A)与电阻R(单位:Ω)之间的函数关系图象大致是( )
A. B.
C. D.
2.研究发现,近视镜的度数y(度)与镜片焦距x(米)成反比例函数关系,小明佩戴的400度近视镜片的焦距为0.25米,经过一段时间的矫正治疗加之注意用眼健康,现在镜片焦距为0.4米,则小明的近视镜度数可以调整为( )
A.500度 B.300度 C.250度 D.200度
3.已知一个长方形的周长为50cm,相邻两边分别为xcm,ycm,则y与x之间的关系式为( )
A.y=50﹣x B.y=25﹣x C.y= D.y=
4.弹簧挂重物后会伸长,测得弹簧长度y(cm)量长为20cm,与所挂物体重量x(kg)间有下面的关系:下列说法不正确的是( )
x 0 1 2 3 4 …
y 8 8.5 9 9.5 10 …
A.x与y都是变量,x是自变量,y是因变量
B.所挂物体为6kg,弹簧长度为11cm
C.物体每增加1kg,弹簧长度就增加0.5cm
D.挂30kg物体时,弹簧长度一定比原长增加15cm
5.某科研小组在网上获取了声音在空气中传播的速度与空气温度关系的一些数据(如表):下列说法错误的是( )
温度/℃ ﹣20 ﹣10 0 10 20 30
声速/(m/s) 318 324 330 336 342 348
A.在这个变化中,自变量是温度,因变量是声速
B.温度越高,声速越快
C.当空气温度为20℃时,声音5s可以传播1740m
D.当温度每升高10℃,声速增加6m/s
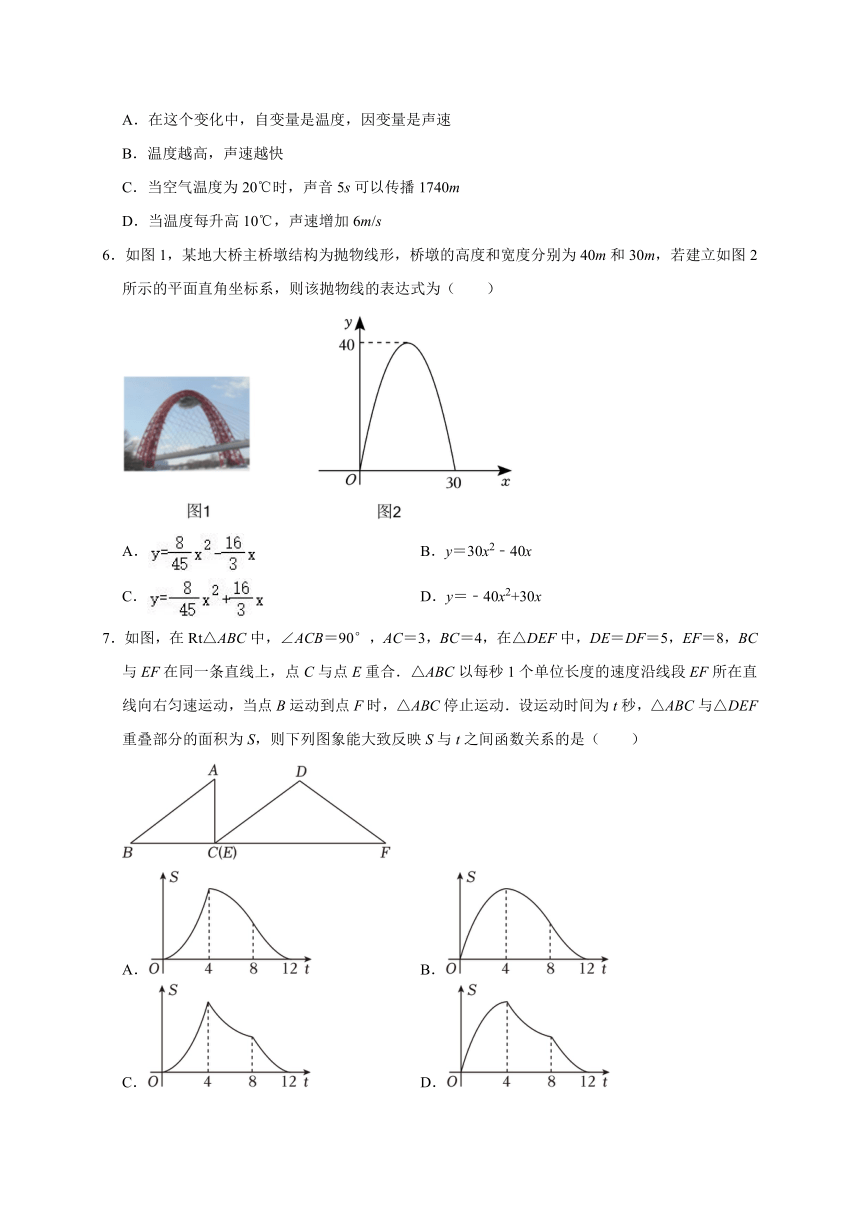
6.如图1,某地大桥主桥墩结构为抛物线形,桥墩的高度和宽度分别为40m和30m,若建立如图2所示的平面直角坐标系,则该抛物线的表达式为( )
A. B.y=30x2﹣40x
C. D.y=﹣40x2+30x
7.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,在△DEF中,DE=DF=5,EF=8,BC与EF在同一条直线上,点C与点E重合.△ABC以每秒1个单位长度的速度沿线段EF所在直线向右匀速运动,当点B运动到点F时,△ABC停止运动.设运动时间为t秒,△ABC与△DEF重叠部分的面积为S,则下列图象能大致反映S与t之间函数关系的是( )
A. B.
C. D.
8.台风影响着人们的生产和生活.人们为研究台风,将研究条件进行一定的合理简化,把近地面风速画在一个以台风中心为原点,以台风半径为横轴,风速为纵轴的坐标系中,并在图中标注了该台风的12级、10级和7级风圈半径,如12级风圈半径是指近地面风速衰减至32.7m/s时,离台风中心的距离约为150km.那么以下关于这场台风的说法中,正确的是( )
A.越靠近台风中心位置,风速越大
B.距台风中心150km处,风速达到最大值
C.10级风圈半径约为280km
D.在某个台风半径达到最大风速之后,随台风半径的增大,风速又逐渐衰减
二.填空题(共6小题)
9.密闭容器内有一定质量的二氧化碳,当容器的体积V(单位:m3)变化时,气体的密度ρ(单位:kg/m)随之变化.已知密度ρ与体积V是反比例函数关系,它的图象如图所示,当V=5m3时,ρ=1.98kg/m3.若3≤V≤9,二氧化碳密度ρ的变化范围 .
10.一支原长为20cm的蜡烛,点燃后,其剩余长度与燃烧时间的关系如表:
烧烧时间/分 10 20 30 40 50
剩余长度/cm 19 18 17 16 15
当这支蜡烛的剩余长度为10cm时,这支蜡烛燃烧了 分钟.
11.某超市购进一批拼装玩具,进价为每个10元,在销售过程中发现,日销售量y(个)与销售单价x(元)之间满足如图所示的一次函数关系,则该超市每天销售这款拼装玩具的最大利润为 元(利润=总销售额﹣总成本).
12.党的二十大报告指出:“高质量发展”是全面建设社会主义现代化的首要任务.在数学中,我们不妨设:在平面直角坐标系内,如果点(m,n)的坐标满足n=m2,那么称点(m,n)为“高质量发展点”.若点A(a,9)是反比例函数y=(k≠0)的图象上的“高质量发展点”,则该反比例函数的解析式为 .
13.为了预防“流感”,某学校对教室采用药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧完后,y与x成反比例(如图).现测得药物8min燃毕,此时室内空气中每立方米的含药量为6mg.研究表明,当空气中每立方米的含药量不低于3mg才有效,那么此次消毒的有效时间是 分钟.
14.已知矩形ABCD中,AB=2AD=8,点E、F分别是边AB、CD的中点,点P为AD边上动点,过点P作与AB平行的直线交AF于点G,连接PE,点M是PE中点,连接MG,则MG的最小值= .
三.解答题(共9小题)
15.某医药研究所研制了一种新药,在试验药效时发现:成人按规定剂量服用后,检测到从第10分钟起每分钟每毫升血液中含药量增加0.3微克,第100分钟达到最高,接着开始衰退.血液中含药量y(微克)与时间x(分钟)的函数关系如图,并发现衰退时y与x成反比例函数关系.
(1)a= ;
(2)分别求出当10≤x≤100和x>100时,y与x之间的函数关系式;
(3)如果每毫升血液中含药量不低于12微克时是有效的,求一次服药后的有效时间是多少分钟?
16.渠县是全国优质黄花主产地,某加工厂加工黄花的成本为30元/千克,根据市场调查发现,批发价定为48元/千克时,每天可销售500千克,为增大市场占有率,在保证盈利的情况下,工厂采取降价措施,批发价每千克降低1元,每天销量可增加50千克.
(1)设批发价每千克降x元,写出工厂每天的利润W元与降价x元之间的函数关系式.
(2)当降价多少元时,工厂每天的利润最大,最大为多少元?
(3)若工厂每天的利润要达到9750元,并让利于民,则定价应为多少元?
17.2022年北京冬奥会期间,某网店直接从工厂购进A、B两款冰墩墩钥匙扣,进货价和销售价如表:(注:利润=销售价﹣进货价)
类别 价格 A款钥匙扣 B款钥匙扣
进货价(元/件) 30 25
销售价(元/件) 45 37
(1)网店第一次用850元购进A、B两款钥匙扣共30件,求两款钥匙扣分别购进的件数;
(2)第一次购进的冰墩墩钥匙扣售完后,该网店计划再次购进A、B两款冰墩墩钥匙扣共80件(进货价和销售价都不变),且进货总价不高于2200元.应如何设计进货方案,才能获得最大销售利润,最大销售利润是多少?
18.某纪念品的进价为每件40元,售价为每件50元,每星期可卖出200个.经市场调查发现:以不低于现售价的价格销售该商品,售价每上涨1元,则每星期少卖4个(每件售价不高于68元),设每件商品销售单价为x(元),每星期销售量为y(个).
(1)求y与x之间的函数关系式,并直接写出自变量x的取值范围;
(2)将该纪念品的销售单价定为多少元时,每星期销售这种产品获得的利润最大?最大利润是多少元?
19.陕西大樱桃发展十分迅速,后来居上,成为我国三大樱桃产地之一,其中,铜川大樱桃最为出名,先后荣获“国家地理标志保护产品”“中国优质甜樱桃之都”等殊荣,每到樱桃成熟的季节,就会有大批的水果商收购樱桃.今年某村在销售前对本地市场进行调查发现:当批发价为2.4万元/吨时,每天可售出13吨,每吨每涨0.2万元,每天的销量将减少1吨,据测算,每吨平均投入成本1万元,为了抢占市场,薄利多销,该村产业合作社决定,批发价不低于2.4万元/吨,不高于4.5万元/吨.设樱桃的批发价为x(万元/吨),每天获得的利润为y(万元),请解答下列问题:
(1)用含x的代数式表示每天樱桃的销售量为 (吨),并求出每天获得的利润y(万元)与批发价x(万元/吨)之间的函数关系式;
(2)若该村每天批发樱桃要盈利15万元,求樱桃的批发价应定为多少万元/吨?
(3)当樱桃的批发价定为多少万元时,每天所获的利润最大,并求出最大利润.
20.由于惯性的作用,行驶中的汽车在刹车后还要继续向前滑行一段距离才能停止,这段距离称为“刹车距离”.为了测定某种型号小型载客汽车的刹车性能(车速不超过140km/h),对这种型号的汽车进行了测试,测得的数据如下表:
刹车时车速v(km/h) 0 10 20 30 40 50 …
刹车距离s(m) 0 2.5 5 7.5 10 12.5 …
请回答下列问题:
(1)在这个变化过程中,自变量是 ,因变量是 .
(2)当刹车时车速为30km/h时,刹车距离是多少米?
(3)观察表中数据可知,当刹车时车速每增加10km/h时,刹车距离增加多少米?该型号汽车某次的刹车距离为20m,推测刹车时的车速是多少?
21.在某场篮球比赛中,运动员甲在距篮下7m的三分线外跳起投篮,球运行的路线大致是抛物线,当球运行的水平距离为4m时,球达到最大高度3.86m,然后准确落入篮圈,篮圈中心到地面的距离为3.05m,建立如图所示的平面直角坐标系.
(1)请求出该抛物线的表达式;
(2)另一运动员乙位于运动员甲与原点O之间,且距离甲为0.4m,原地起跳后成功盖帽拦截运动员甲投出的球,问:运动员乙起跳后双手达到的高度至少为多少?(结果精确到0.01m)
22.1~6个月的婴儿生长发育非常快,他们的体重y(g)和月龄x(月)的关系可以用y=a+700x来表示,其中a是婴儿出生时的体重.下面表格表示在1~6个月之间,这个婴儿的体重y与月龄x之间的关系.
月龄x/月 1 2 3 4 5 6
体重y/g 4200 4900 5600 6300 7000 7700
(1)上表反映的变化过程中, 是自变量, 是因变量;
(2)利用表中数据直接写出该婴儿体重y(g)和月龄x(月)之间的关系式为 ;
(3)若某婴儿出生时的体重为4000g,请计算该婴儿第6个月时体重是多少g?
应用题模型—建立函数模型解决实际问题 数学解题模型与方法
参考答案与试题解析
一.选择题(共8小题)
1.小明学习了物理中的欧姆定律发现:电阻两端的电压=电流强度×电流通过的电阻.已知某滑动变阻器两端电压恒定,当变阻器的电阻调节为10Ω时,测得通过该变阻器的电流为24A,则通过该滑动变阻器的电流I(单位:A)与电阻R(单位:Ω)之间的函数关系图象大致是( )
A. B.
C. D.
【答案】A
【解答】解:∵电阻两端的电压=电流强度×电流通过的电阻,
∴I=,
∵当R=10Ω时,I=24A,
∴=24,
∴U=240(V),
∴I=,
∴电流I与电阻R成反比例函数关系,
故答案A符合题意,
答案B是一次函数,故不符合题意,
答案C是正比例函数,故不符合题意,
答案D是二次函数,故不符合题意,
故选:A.
2.研究发现,近视镜的度数y(度)与镜片焦距x(米)成反比例函数关系,小明佩戴的400度近视镜片的焦距为0.25米,经过一段时间的矫正治疗加之注意用眼健康,现在镜片焦距为0.4米,则小明的近视镜度数可以调整为( )
A.500度 B.300度 C.250度 D.200度
【答案】C
【解答】解:设y=(k≠0),
∵x=0.25时,y=400,
∴,
∴k=100,
∴y与x的函数关系式为:y=,
当x=0.4时,y==250,
∴小明的近视镜度数可以调整为250度.
故选:C.
3.已知一个长方形的周长为50cm,相邻两边分别为xcm,ycm,则y与x之间的关系式为( )
A.y=50﹣x B.y=25﹣x C.y= D.y=
【答案】B
【解答】解:由题意得,2(x+y)=50,
解得y=25﹣x,
故选:B.
4.弹簧挂重物后会伸长,测得弹簧长度y(cm)量长为20cm,与所挂物体重量x(kg)间有下面的关系:下列说法不正确的是( )
x 0 1 2 3 4 …
y 8 8.5 9 9.5 10 …
A.x与y都是变量,x是自变量,y是因变量
B.所挂物体为6kg,弹簧长度为11cm
C.物体每增加1kg,弹簧长度就增加0.5cm
D.挂30kg物体时,弹簧长度一定比原长增加15cm
【答案】D
【解答】解:由题意可得,x与y都是变量,x是自变量,y是因变量,
∴选项A不符合题意;
由题意可得,在该弹簧弹性限度范围内所挂重物每增加1kg弹簧就多伸长0.5cm,则所挂物体为6kg,可计算得弹簧长度为11cm,挂30kg物体时,如果超出该弹簧的弹性限度范围,则弹簧长度就不会比原长增加15cm.
∴选项B、C不符合题意,选项D符合题意,
故选:D.
5.某科研小组在网上获取了声音在空气中传播的速度与空气温度关系的一些数据(如表):下列说法错误的是( )
温度/℃ ﹣20 ﹣10 0 10 20 30
声速/(m/s) 318 324 330 336 342 348
A.在这个变化中,自变量是温度,因变量是声速
B.温度越高,声速越快
C.当空气温度为20℃时,声音5s可以传播1740m
D.当温度每升高10℃,声速增加6m/s
【答案】C
【解答】解:由函数的定义可得,在这个变化中,自变量是温度,因变量是声速,
∴选项A不符合题意;
∵由表格信息可得,温度越高,声速越快,
∴选项B不符合题意;
∵当空气温度为20℃时,声音5s可以传播距离为342×20=1740(m),
∴选项C符合题意;
∵由题意得当温度每升高10℃,声速增加6m/s,
∴选项D不符合题意;
故选:C.
6.如图1,某地大桥主桥墩结构为抛物线形,桥墩的高度和宽度分别为40m和30m,若建立如图2所示的平面直角坐标系,则该抛物线的表达式为( )
A. B.y=30x2﹣40x
C. D.y=﹣40x2+30x
【答案】C
【解答】解:由二次函数的图象可得,抛物线与x轴的交点坐标为(0,0)和(30,0),
∴对称轴为x==15,
∵桥墩的高度为40m,
∴抛物线的顶点坐标为(15,40),
设抛物线的解析式为y=a(x﹣15)2+40(a≠0),
把(0,0)代入上式得,
a×152+40=0,
∴a=﹣,
∴该抛物线的表达式为y=﹣(x﹣15)2+40,
即y=﹣x2+x,
故选:C.
7.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,在△DEF中,DE=DF=5,EF=8,BC与EF在同一条直线上,点C与点E重合.△ABC以每秒1个单位长度的速度沿线段EF所在直线向右匀速运动,当点B运动到点F时,△ABC停止运动.设运动时间为t秒,△ABC与△DEF重叠部分的面积为S,则下列图象能大致反映S与t之间函数关系的是( )
A. B.
C. D.
【答案】A
【解答】解:过点D作DH⊥CB于H,
∵DE=DF=5,EF=8,
∴EH=FH=EF=4,
∴DH==3,
当0≤t<4时,
如图,重叠部分为△EPQ,此时EQ=t,PQ∥DH,
∴△EPQ∽△EDH,
∴,即,
∴PQ=t,
∴S==2,
当4≤t<8时,
如图,重叠部分为四边形POC′B′,此时BB′=CC′=t,PB∥DE.
∴B′F=BC+CF﹣BB′=12﹣t,FC=8﹣t,
∵PB∥DE,
∴△PBF∽△DCF,
∴,
又S△DCF=,
∴,
∵DH⊥BC.∠AB′C′=90°,
∴AC′∥DH,
∴△C′QF∽△HFD.
∴,即,
∴,
∴S=S△PB′F﹣S△C′QF==,
当8≤t≤12时
如图,重叠部分为四边形△PFB′,此时BB′=CC′=t,PB′∥DE.
∴B′F=BC+CF﹣BB′=12﹣t,
∵PB′∥DE.
∴△PB′F∽△DCF,
∴,即,
∴,S=S△PB′F=,
综上,
∴符合题意的函数图象是选项A.
故选:A.
8.台风影响着人们的生产和生活.人们为研究台风,将研究条件进行一定的合理简化,把近地面风速画在一个以台风中心为原点,以台风半径为横轴,风速为纵轴的坐标系中,并在图中标注了该台风的12级、10级和7级风圈半径,如12级风圈半径是指近地面风速衰减至32.7m/s时,离台风中心的距离约为150km.那么以下关于这场台风的说法中,正确的是( )
A.越靠近台风中心位置,风速越大
B.距台风中心150km处,风速达到最大值
C.10级风圈半径约为280km
D.在某个台风半径达到最大风速之后,随台风半径的增大,风速又逐渐衰减
【答案】D
【解答】解:A、根据图象可知,在图象的前段部分,风速随台风半径的增大而增大,则越靠近台风中心位置,风速越小(最小为10m/s),故A选项不符合题意;
B、根据图象可知,台风半径小于100km时,风速已达到最大值,故B选项不符合题意;
C、根据图象可知,10级风圈的台风半径为200km,风速为24.5m/s,故C选项不符合题意;
D、根据图象可知,风速先是随台风半径的增大而增大,风速达到最大之后,又随台风半径的增大而减小,故D选项符合题意.
故选:D.
二.填空题(共6小题)
9.密闭容器内有一定质量的二氧化碳,当容器的体积V(单位:m3)变化时,气体的密度ρ(单位:kg/m)随之变化.已知密度ρ与体积V是反比例函数关系,它的图象如图所示,当V=5m3时,ρ=1.98kg/m3.若3≤V≤9,二氧化碳密度ρ的变化范围 1.1≤ρ≤3.3 .
【答案】1.1≤ρ≤3.3.
【解答】解:∵密度ρ与体积V是反比例函数关系,
∴设,
∵当V=5m3时,ρ=1.98kg/m3,
∴,
∴k=1.98×5=9.9,
∴密度ρ关于体积V的函数解析式为:,
观察函数图象可知,ρ随V的增大而减小,
当V=3m3时,ρ==3.3(kg/m3),
当V=9m3时,ρ==1.1(kg/m3),
∴当3≤V≤9时,1.1≤ρ≤3.3(kg/m3),
即二氧化碳密度ρ的变化范围是1.1≤ρ≤3.3(kg/m3),
故答案为:1.1≤ρ≤3.3.
10.一支原长为20cm的蜡烛,点燃后,其剩余长度与燃烧时间的关系如表:
烧烧时间/分 10 20 30 40 50
剩余长度/cm 19 18 17 16 15
当这支蜡烛的剩余长度为10cm时,这支蜡烛燃烧了 100 分钟.
【答案】100.
【解答】解:设燃烧x分钟时该蜡烛的剩余长度为ycm,
由题意得该蜡烛每燃烧10分钟剩余长度减少1cm,
∴y=﹣x+20,
∴当y=10时,
﹣x+20=10,
解得x=100,
故答案为:100.
11.某超市购进一批拼装玩具,进价为每个10元,在销售过程中发现,日销售量y(个)与销售单价x(元)之间满足如图所示的一次函数关系,则该超市每天销售这款拼装玩具的最大利润为 800 元(利润=总销售额﹣总成本).
【答案】800.
【解答】解:设日销售量y与销售单价x之间的函数关系式为y=kx+b(k≠0),
∵点(25,50),(35,30)在函数图象上,
∴,
解得,
∴y=﹣2x+100,
设每天的销售利润为w元,
则w=(x﹣10) y
=(x﹣10)(﹣2x+100)
=﹣2x2+120x﹣1000
=﹣2(x﹣30)2+800,
∵﹣2<0,
∴开口向下,
∴当x=30时,w最大值=800,
即超市每天销售这款拼装玩具的最大利润为800元,
故答案为:800.
12.党的二十大报告指出:“高质量发展”是全面建设社会主义现代化的首要任务.在数学中,我们不妨设:在平面直角坐标系内,如果点(m,n)的坐标满足n=m2,那么称点(m,n)为“高质量发展点”.若点A(a,9)是反比例函数y=(k≠0)的图象上的“高质量发展点”,则该反比例函数的解析式为 y=或y=﹣ .
【答案】y=或y=﹣.
【解答】解:将(a,9)代入y=(k≠0)中得,=9,
∴k=9a,
∵点A(a,9)是“高质量发展点“,
∴a2=9,
解方程组得,
或,
则该反比例函数的解析式为y=或y=﹣.
13.为了预防“流感”,某学校对教室采用药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧完后,y与x成反比例(如图).现测得药物8min燃毕,此时室内空气中每立方米的含药量为6mg.研究表明,当空气中每立方米的含药量不低于3mg才有效,那么此次消毒的有效时间是 12 分钟.
【答案】12.
【解答】解:设药物燃烧时y与x的函数关系式为y=kx(k>0),
把(8,6)代入上式得,8k=6,
∴k=,
∴y=x(0≤x≤8);
设药物燃烧完后y与x的函数关系式为y=(k1>0),
把(8,6)代入上式得,=6,
∴k1=48,
∴y=(x>8),
当y=3时,x=3,x=4;=3,x=16,
∴此次消毒的有效时间为16﹣4=12(分钟),
故答案为:12.
14.已知矩形ABCD中,AB=2AD=8,点E、F分别是边AB、CD的中点,点P为AD边上动点,过点P作与AB平行的直线交AF于点G,连接PE,点M是PE中点,连接MG,则MG的最小值= .
【答案】.
【解答】解:方法一:如图,过点M作MN⊥PG于点N,取AP的中点H,连接MH,EF,
设AP=x,则AH=PH=x,
∵四边形ABCD是矩形,且AB=2AD=8,
∴AB=CD=8,AD=4,∠BAD=∠D=90°,AB∥CD,
∵PG∥AB,
∴PG∥CD,
∴∠APG=∠D=90°,
∵点E、F分别是边AB、CD的中点,AB=2AD=8,
∴AE=AD=DF=4,
∵点M是PE中点,点H是AP的中点,
∴MH∥AB,MH=AE=2,
∴∠PHM=∠BAD=90°,
∵MN⊥PG,
∴∠MNP=∠MNG=90°=∠PHM=∠APG,
∴四边形MNPH是矩形,
∴PN=MH=2,MN=PH=x,
∵AD=DF,∠D=90°,
∴△ADF是等腰直角三角形,
∴∠AFD=45°,
∵PG∥CD,
∴∠AGP=∠AFD=45°,
∵∠APG=90°,
∴△APG是等腰直角三角形,
∴PG=AP=x,
∴NG=PG﹣PN=x﹣2,
在Rt△MNG中,MG2=MN2+NG2=(x)2+(x﹣2)2=(x﹣)2+,
∵>0,
∴当x=时,MG2取得最小值,
∵MG===,
∴MG的最小值为,
故答案为:.
方法二:如图,以点D为原点,直线CD为x轴,直线AD为y轴建立平面直角坐标系,
∵四边形ABCD是矩形,且AB=2AD=8,
∴A(0,4),B(﹣8,4),C(﹣8,0),D(0,0),
∵点E、F分别是边AB、CD的中点,
∴E(﹣4,4),F(﹣4,0),
设P(0,t),
∵点M是PE中点,
∴M(﹣2,),
设直线AG的解析式为y=kx+b,则,
解得:,
∴直线AG的解析式为y=x+4,
∵PG∥x轴交AF于G,
∴G(t﹣4,t),
∴MG2=[(t﹣4)﹣(﹣2)]2+(t﹣)2=t2﹣6t+8=(t﹣)2+,
∵>0,
∴MG2有最小值,
∵MG>0,
∴MG的最小值为=,
故答案为:.
三.解答题(共9小题)
15.某医药研究所研制了一种新药,在试验药效时发现:成人按规定剂量服用后,检测到从第10分钟起每分钟每毫升血液中含药量增加0.3微克,第100分钟达到最高,接着开始衰退.血液中含药量y(微克)与时间x(分钟)的函数关系如图,并发现衰退时y与x成反比例函数关系.
(1)a= 27 ;
(2)分别求出当10≤x≤100和x>100时,y与x之间的函数关系式;
(3)如果每毫升血液中含药量不低于12微克时是有效的,求一次服药后的有效时间是多少分钟?
【答案】(1)27;
(2)当10≤x≤100时:y=0.3x﹣3,
当x>100时,y=;
(3)175分钟.
【解答】解:(1)∵从第10分钟起每分钟每毫升血液中含药量增加0.3微克,第100分钟达到最高,
∴a=(100﹣10)×0.3=27,
故答案为:27.
(2)当10≤x≤100时设y=kx+b,代入(10,0)和(100,27)得:
,
解得:,
∴当10≤x≤100时:y=0.3x﹣3,
当x>100时,设y=,代入(100,27),
∴m=100×27=2700,
当x>100时,y=;
(3)上升阶段药效达到12微克时间,
根据y=0.3x﹣3,
令y=12则12=0.3x﹣3,
解得:x=50分钟,
衰退阶段药效达到12微克时间,
由y=,
令y=12,则12=,
解得:x=225分钟,
∴一次服药后的有效时间是175分钟.
16.渠县是全国优质黄花主产地,某加工厂加工黄花的成本为30元/千克,根据市场调查发现,批发价定为48元/千克时,每天可销售500千克,为增大市场占有率,在保证盈利的情况下,工厂采取降价措施,批发价每千克降低1元,每天销量可增加50千克.
(1)设批发价每千克降x元,写出工厂每天的利润W元与降价x元之间的函数关系式.
(2)当降价多少元时,工厂每天的利润最大,最大为多少元?
(3)若工厂每天的利润要达到9750元,并让利于民,则定价应为多少元?
【答案】(1)W=﹣50x2+400x+9000;
(2)当降价4元时,工厂每天的利润最大,最大为9800元;
(3)定价应为43元.
【解答】解:(1)由题意得:
W=(48﹣30﹣x)(500+50x),
即W=﹣50x2﹣400x+9000
答:工厂每天的利润W元与降价x元之间的函数关系为W=﹣50x2+400x+9000;
(2)由(1)得:
W=﹣50x2+400x+9000=﹣50(x﹣4)2+9800
.﹣50<0,
.x=4时,W最大为9800,
即当降价4元时,工厂每天的利润最大,最大为9800元.
(3)﹣50x2+400x+9000=9750解得:x1=3,x2=5,
∵让利于民,
.x1=3不合题意,舍去,
定价应为48﹣5=43(元),
答:定价应为43元.
17.2022年北京冬奥会期间,某网店直接从工厂购进A、B两款冰墩墩钥匙扣,进货价和销售价如表:(注:利润=销售价﹣进货价)
类别 价格 A款钥匙扣 B款钥匙扣
进货价(元/件) 30 25
销售价(元/件) 45 37
(1)网店第一次用850元购进A、B两款钥匙扣共30件,求两款钥匙扣分别购进的件数;
(2)第一次购进的冰墩墩钥匙扣售完后,该网店计划再次购进A、B两款冰墩墩钥匙扣共80件(进货价和销售价都不变),且进货总价不高于2200元.应如何设计进货方案,才能获得最大销售利润,最大销售利润是多少?
【答案】(1)购进A款钥匙扣20件,B款钥匙扣10件.
(2)当购进40件A款钥匙扣,购进40件B款钥匙扣时,获得最大利润,最大利润为1080元.
【解答】解:(1)设购进A款钥匙扣x件,B款钥匙扣y件,
由题意得,,
解得,
答:购进A款钥匙扣20件,B款钥匙扣10件.
(2)设购进m件A款钥匙扣,则购进(80﹣m)件B款钥匙扣,
则30m+25(80﹣m)≤2200,
解得m≤40.
设再次购进后获得的总利润为w元,
则w=(45﹣30)m+(37﹣25)(80﹣m)=3m+960.
∵3>0,
∴w随m的增大而增大,
∴当m=40时,w最大值=3×40+960=1080,
此时80﹣m=40.
答:当购进40件A款钥匙扣,购进40件B款钥匙扣时,获得最大利润,最大利润为1080元.
18.某纪念品的进价为每件40元,售价为每件50元,每星期可卖出200个.经市场调查发现:以不低于现售价的价格销售该商品,售价每上涨1元,则每星期少卖4个(每件售价不高于68元),设每件商品销售单价为x(元),每星期销售量为y(个).
(1)求y与x之间的函数关系式,并直接写出自变量x的取值范围;
(2)将该纪念品的销售单价定为多少元时,每星期销售这种产品获得的利润最大?最大利润是多少元?
【答案】(1)y=﹣4x+400,50≤x≤68.
(2)单价定为68元时,每星期销售这种产品获得的利润最大,最大利润是3584元.
【解答】解:(1)由题意得:
y=200﹣4(x﹣50)
=﹣4x+400.
自变量x的取值范围为50≤x≤68.
(2)设每星期销售这种产品获得的利润为w元,
由题意得:
w=(x﹣40)(﹣4x+400)
=﹣4x2+560x﹣16000
=﹣4(x﹣70)2+3600,
∵a=﹣4<0,50≤x≤68,
∴当x=68时,w取得最大值,最大值为:﹣4(68﹣70)2+3600=3584,
答:单价定为68元时,每星期销售这种产品获得的利润最大,最大利润是3584元.
19.陕西大樱桃发展十分迅速,后来居上,成为我国三大樱桃产地之一,其中,铜川大樱桃最为出名,先后荣获“国家地理标志保护产品”“中国优质甜樱桃之都”等殊荣,每到樱桃成熟的季节,就会有大批的水果商收购樱桃.今年某村在销售前对本地市场进行调查发现:当批发价为2.4万元/吨时,每天可售出13吨,每吨每涨0.2万元,每天的销量将减少1吨,据测算,每吨平均投入成本1万元,为了抢占市场,薄利多销,该村产业合作社决定,批发价不低于2.4万元/吨,不高于4.5万元/吨.设樱桃的批发价为x(万元/吨),每天获得的利润为y(万元),请解答下列问题:
(1)用含x的代数式表示每天樱桃的销售量为 ﹣5x+25 (吨),并求出每天获得的利润y(万元)与批发价x(万元/吨)之间的函数关系式;
(2)若该村每天批发樱桃要盈利15万元,求樱桃的批发价应定为多少万元/吨?
(3)当樱桃的批发价定为多少万元时,每天所获的利润最大,并求出最大利润.
【答案】(1)﹣5x+25,y=﹣5x2+30x﹣25.
(2)4.
(3)当批发价定为3万元/吨时,每天获得的利润最大,最大利润是20万元.
【解答】解:(1)每天樱桃的销售量为13﹣=﹣5x+25(吨),
根据题意得,y=(﹣5x+25)(x﹣1)=﹣5x2+30x﹣25,
∴每天获得的利润y(万元)与批发价x(万元/吨)之间的函数关系式为y=﹣5x2+30x﹣25.
故答案为:﹣5x+25.
(2)根据题意可得﹣5x2+30x﹣25=15,
解得x1=2,x2=4,
∵2.4≤x≤4.5,
∴x=4,
答:若该村每天批发樱桃要盈利15万元,樱桃的批发价应定为4万元/吨.
(3)y=﹣5x2+30x﹣25=﹣5(x﹣3)2+20,
∵2.4≤x≤4.5,
∴当x=3时,y有最大值,y最大值=20,
∴当批发价定为3万元/吨时,每天获得的利润最大,最大利润是20万元.
20.由于惯性的作用,行驶中的汽车在刹车后还要继续向前滑行一段距离才能停止,这段距离称为“刹车距离”.为了测定某种型号小型载客汽车的刹车性能(车速不超过140km/h),对这种型号的汽车进行了测试,测得的数据如下表:
刹车时车速v(km/h) 0 10 20 30 40 50 …
刹车距离s(m) 0 2.5 5 7.5 10 12.5 …
请回答下列问题:
(1)在这个变化过程中,自变量是 刹车时车速v ,因变量是 刹车距离s .
(2)当刹车时车速为30km/h时,刹车距离是多少米?
(3)观察表中数据可知,当刹车时车速每增加10km/h时,刹车距离增加多少米?该型号汽车某次的刹车距离为20m,推测刹车时的车速是多少?
【答案】(1)刹车时车速v,刹车距离s;
(2)当刹车时车速为30km/h时,刹车距离是7.5米;
(3)当刹车时车速每增加10km/h时,刹车距离增加2.5米;当该型号汽车某次的刹车距离为20m时,刹车时的车速是80km/h.
【解答】解:(1)由题意得,
在这个变化过程中,自变量是刹车时车速v,因变量是刹车距离s,
故答案为:刹车时车速v,刹车距离s;
(2)由题意得,当刹车时车速为30km/h时,刹车距离是7.5米,
答:当刹车时车速为30km/h时,刹车距离是7.5米;
(3)由表中数据可知,当刹车时车速每增加10km/h时,刹车距离增加2.5米,
∴刹车距离s和刹车时车速v间的函数关系式为:s=v,
整理,得s=0.25v,
由题意可得0.25v=20,
解得v=80,
答:当刹车时车速每增加10km/h时,刹车距离增加2.5米;当该型号汽车某次的刹车距离为20m时,刹车时的车速是80km/h.
21.在某场篮球比赛中,运动员甲在距篮下7m的三分线外跳起投篮,球运行的路线大致是抛物线,当球运行的水平距离为4m时,球达到最大高度3.86m,然后准确落入篮圈,篮圈中心到地面的距离为3.05m,建立如图所示的平面直角坐标系.
(1)请求出该抛物线的表达式;
(2)另一运动员乙位于运动员甲与原点O之间,且距离甲为0.4m,原地起跳后成功盖帽拦截运动员甲投出的球,问:运动员乙起跳后双手达到的高度至少为多少?(结果精确到0.01m)
【答案】(1)y=﹣0.09x2+3.86.
(2)2.69米.
【解答】解:(1)由于球运行的水平距离为4m时,球达到最大高度3.86m,
则设该抛物线的表达式为y=ax2+3.86(a≠0),
代入(3,3.05)得,9a+3.86=3.05,
解得a=﹣0.09,
∴该抛物线的表达式为y=﹣0.09x2+3.86.
(2)∵4﹣0.4=3.6,
∴运动员乙所在位置的横坐标为﹣3.6,
当x=﹣3.6时,y=﹣0.09×(﹣3.6)2+3.86≈2.69,
答:运动员乙起跳后双手达到的高度至少为2.69米.
22.1~6个月的婴儿生长发育非常快,他们的体重y(g)和月龄x(月)的关系可以用y=a+700x来表示,其中a是婴儿出生时的体重.下面表格表示在1~6个月之间,这个婴儿的体重y与月龄x之间的关系.
月龄x/月 1 2 3 4 5 6
体重y/g 4200 4900 5600 6300 7000 7700
(1)上表反映的变化过程中, 月龄x 是自变量, 体重y 是因变量;
(2)利用表中数据直接写出该婴儿体重y(g)和月龄x(月)之间的关系式为 y=700x+3500 ;
(3)若某婴儿出生时的体重为4000g,请计算该婴儿第6个月时体重是多少g?
【答案】(1)月龄x;体重y
(2)y=700x+3500;
(3)该婴儿第6个月时体重是8200g.
【解答】解:(1)由题意得,
上表反映的变化过程中,月龄x是自变量,体重y是因变量,
故答案为:月龄x,体重y;
(2)由题意得,
a+700×1=4200,
解得a=3500,
利用表中数据直接写出该婴儿体重y(g)和月龄x(月)之间的关系式为:y=700x+3500,
故答案为:y=700x+3500;
(3)若出生时体重为4000g,则体重和月龄之间的关系为:y=4000+700x
当x=6时,y=4000+700×6=8200(g),
答:该婴儿第6个月时体重是8200g.
【解题模型与方法】
1、解决函数应用问题的基本思路方法
从终极目标量开始,建立与之相关的等量关系,可能会引出新的目标量,此时又以建立与新目标量相关的等量关系,...,.如此不断建立与新目标量相关的等量关系,直至最后一个等量关系中出现的量均为题设中的已知量与所设出的量为止.按照此法,通过不断的寻求该目标量的等量关系,可以逐步把题目中的各种信息、条件融合在目标量之下,进而将题目所涉及的量的关系程序化,从而构建数学模型,达到解决问题的目的.
2、用函数构建数学模型解决实际问题的步骤
(1)观察实际情景:对实际问题中的变化过程进行分析;
(2)发现和提出问题:析出常量、变量及其相互关系;
(3)收集数据、分析数据:明确其运动变化的基本特征,从而确定它的运动变化类型;
(4)选择函数模型:根据分析结果,选择适当的函数类型构建数学模型,将实际问题
化归为数学问题;
(5)求解函数模型:通过运算推理,求解函数模型;
(6)检验模型:利用函 数模型的解说明实际问题的变化规律,达到解决问题的目的.
【典型例题】
例题1.如图,在Rt△ABC中,∠C=90°,AC=3厘米,CB=4厘米.两个动点P,Q分别从A,C两点同时按顺时针方向沿△ABC的边运动.当点Q运动到点A时,P,Q两点运动即停止.点P,Q的运动速度分别为1厘米/秒、2厘米/秒,设点P运动的时间为t(秒).记线段PQ与从点P按顺时针方向沿△ABC的边到点Q的折线段所围成的图形的面积为S(平方厘米).
(1)用含t的代数式表示PC的长;
(2)当点P,Q运动时,求S与时间t的函数关系式,并写出自变量t的取值范围;
(3)点P,Q在运动的过程中,S有最大值吗?若有,请求出最大值;若没有,请说明理由.
解:(1)∵Rt△ABC中,∠C=90°,AC=3厘米,CB=4厘米,
∴AB=5厘米.
∵(4+5)÷2=秒.
∴P运动的最大距离为=厘米,
∴当点P在AC边上运动时,PC=3﹣t;
当点P在CB边上运动时,PC=t﹣3.
(2)当0<t≤2时,点P在AC边上,点Q在CB边上,如图所示,
∵AC=3,BC=4,AB=5,点P,Q的运动速度分别为1厘米/秒、2厘米/秒,
∴AP=1,CP=3﹣t,CQ=2t,
∵∠C=90°,
∴以P,C,Q三点为顶点的三角形是直角三角形.
S=S△PCQ=CP CQ=(3﹣t)×2t=﹣t2+3t,
当2<1≤3时,点P在AC边上,点Q在AB边上,如图所示,
∵AC=3,BC=4,AB=5,点P,Q的运动速度分别为1厘米/秒、2厘米/秒,
∴AP=t,AQ=9﹣2t,
∴线段PQ与从点P按顺时针方向沿△ABC的边到点Q的折线段所围成的图形为四边形PCBO.
此时S=S△CAB﹣S△APQ,过点P作PD⊥AQ于D.
∵∠A=∠A,∠ADP=∠ACB.
∴△ADP∽△ACB,
∴,即 ,解得 .
∴S△APQ===,
∴S=S△CAB﹣S△NPQ=﹣()=.
当 时,点P在CB边上,点Q在AB边上,如图所示.
由题知,AC=3,BC=4,AB=5,CP=t﹣3,BP=7﹣t,BQ=2t﹣4,
∴线段PQ与从点P按顺时针方向沿△ABC的边到点Q的折线段所围成的图形为三角形PQB.
此时,S=S△QPB,过点P作 PE⊥QB 于E.
∵∠B=∠B,∠BEP=∠BCA,
∴△BEP∽△BCA,
∴,即
解得 ,
∴.
综上,,
(3)由(2)知:,当0<t≤2时,,
当 时,S有最大值为 ;
当2<t≤3时,.
∵,当 时,函数值S随自变量t的增大而增大,
∴当t=3时,S有最大值为 ;
当 时,.
当 ,S有最大值为 ,
综上,当 时,S有最大值为 .
常考经典试题同步检测
考试范围:应用题;考试时间:100分钟;
一.选择题(共8小题)
1.小明学习了物理中的欧姆定律发现:电阻两端的电压=电流强度×电流通过的电阻.已知某滑动变阻器两端电压恒定,当变阻器的电阻调节为10Ω时,测得通过该变阻器的电流为24A,则通过该滑动变阻器的电流I(单位:A)与电阻R(单位:Ω)之间的函数关系图象大致是( )
A. B.
C. D.
2.研究发现,近视镜的度数y(度)与镜片焦距x(米)成反比例函数关系,小明佩戴的400度近视镜片的焦距为0.25米,经过一段时间的矫正治疗加之注意用眼健康,现在镜片焦距为0.4米,则小明的近视镜度数可以调整为( )
A.500度 B.300度 C.250度 D.200度
3.已知一个长方形的周长为50cm,相邻两边分别为xcm,ycm,则y与x之间的关系式为( )
A.y=50﹣x B.y=25﹣x C.y= D.y=
4.弹簧挂重物后会伸长,测得弹簧长度y(cm)量长为20cm,与所挂物体重量x(kg)间有下面的关系:下列说法不正确的是( )
x 0 1 2 3 4 …
y 8 8.5 9 9.5 10 …
A.x与y都是变量,x是自变量,y是因变量
B.所挂物体为6kg,弹簧长度为11cm
C.物体每增加1kg,弹簧长度就增加0.5cm
D.挂30kg物体时,弹簧长度一定比原长增加15cm
5.某科研小组在网上获取了声音在空气中传播的速度与空气温度关系的一些数据(如表):下列说法错误的是( )
温度/℃ ﹣20 ﹣10 0 10 20 30
声速/(m/s) 318 324 330 336 342 348
A.在这个变化中,自变量是温度,因变量是声速
B.温度越高,声速越快
C.当空气温度为20℃时,声音5s可以传播1740m
D.当温度每升高10℃,声速增加6m/s
6.如图1,某地大桥主桥墩结构为抛物线形,桥墩的高度和宽度分别为40m和30m,若建立如图2所示的平面直角坐标系,则该抛物线的表达式为( )
A. B.y=30x2﹣40x
C. D.y=﹣40x2+30x
7.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,在△DEF中,DE=DF=5,EF=8,BC与EF在同一条直线上,点C与点E重合.△ABC以每秒1个单位长度的速度沿线段EF所在直线向右匀速运动,当点B运动到点F时,△ABC停止运动.设运动时间为t秒,△ABC与△DEF重叠部分的面积为S,则下列图象能大致反映S与t之间函数关系的是( )
A. B.
C. D.
8.台风影响着人们的生产和生活.人们为研究台风,将研究条件进行一定的合理简化,把近地面风速画在一个以台风中心为原点,以台风半径为横轴,风速为纵轴的坐标系中,并在图中标注了该台风的12级、10级和7级风圈半径,如12级风圈半径是指近地面风速衰减至32.7m/s时,离台风中心的距离约为150km.那么以下关于这场台风的说法中,正确的是( )
A.越靠近台风中心位置,风速越大
B.距台风中心150km处,风速达到最大值
C.10级风圈半径约为280km
D.在某个台风半径达到最大风速之后,随台风半径的增大,风速又逐渐衰减
二.填空题(共6小题)
9.密闭容器内有一定质量的二氧化碳,当容器的体积V(单位:m3)变化时,气体的密度ρ(单位:kg/m)随之变化.已知密度ρ与体积V是反比例函数关系,它的图象如图所示,当V=5m3时,ρ=1.98kg/m3.若3≤V≤9,二氧化碳密度ρ的变化范围 .
10.一支原长为20cm的蜡烛,点燃后,其剩余长度与燃烧时间的关系如表:
烧烧时间/分 10 20 30 40 50
剩余长度/cm 19 18 17 16 15
当这支蜡烛的剩余长度为10cm时,这支蜡烛燃烧了 分钟.
11.某超市购进一批拼装玩具,进价为每个10元,在销售过程中发现,日销售量y(个)与销售单价x(元)之间满足如图所示的一次函数关系,则该超市每天销售这款拼装玩具的最大利润为 元(利润=总销售额﹣总成本).
12.党的二十大报告指出:“高质量发展”是全面建设社会主义现代化的首要任务.在数学中,我们不妨设:在平面直角坐标系内,如果点(m,n)的坐标满足n=m2,那么称点(m,n)为“高质量发展点”.若点A(a,9)是反比例函数y=(k≠0)的图象上的“高质量发展点”,则该反比例函数的解析式为 .
13.为了预防“流感”,某学校对教室采用药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧完后,y与x成反比例(如图).现测得药物8min燃毕,此时室内空气中每立方米的含药量为6mg.研究表明,当空气中每立方米的含药量不低于3mg才有效,那么此次消毒的有效时间是 分钟.
14.已知矩形ABCD中,AB=2AD=8,点E、F分别是边AB、CD的中点,点P为AD边上动点,过点P作与AB平行的直线交AF于点G,连接PE,点M是PE中点,连接MG,则MG的最小值= .
三.解答题(共9小题)
15.某医药研究所研制了一种新药,在试验药效时发现:成人按规定剂量服用后,检测到从第10分钟起每分钟每毫升血液中含药量增加0.3微克,第100分钟达到最高,接着开始衰退.血液中含药量y(微克)与时间x(分钟)的函数关系如图,并发现衰退时y与x成反比例函数关系.
(1)a= ;
(2)分别求出当10≤x≤100和x>100时,y与x之间的函数关系式;
(3)如果每毫升血液中含药量不低于12微克时是有效的,求一次服药后的有效时间是多少分钟?
16.渠县是全国优质黄花主产地,某加工厂加工黄花的成本为30元/千克,根据市场调查发现,批发价定为48元/千克时,每天可销售500千克,为增大市场占有率,在保证盈利的情况下,工厂采取降价措施,批发价每千克降低1元,每天销量可增加50千克.
(1)设批发价每千克降x元,写出工厂每天的利润W元与降价x元之间的函数关系式.
(2)当降价多少元时,工厂每天的利润最大,最大为多少元?
(3)若工厂每天的利润要达到9750元,并让利于民,则定价应为多少元?
17.2022年北京冬奥会期间,某网店直接从工厂购进A、B两款冰墩墩钥匙扣,进货价和销售价如表:(注:利润=销售价﹣进货价)
类别 价格 A款钥匙扣 B款钥匙扣
进货价(元/件) 30 25
销售价(元/件) 45 37
(1)网店第一次用850元购进A、B两款钥匙扣共30件,求两款钥匙扣分别购进的件数;
(2)第一次购进的冰墩墩钥匙扣售完后,该网店计划再次购进A、B两款冰墩墩钥匙扣共80件(进货价和销售价都不变),且进货总价不高于2200元.应如何设计进货方案,才能获得最大销售利润,最大销售利润是多少?
18.某纪念品的进价为每件40元,售价为每件50元,每星期可卖出200个.经市场调查发现:以不低于现售价的价格销售该商品,售价每上涨1元,则每星期少卖4个(每件售价不高于68元),设每件商品销售单价为x(元),每星期销售量为y(个).
(1)求y与x之间的函数关系式,并直接写出自变量x的取值范围;
(2)将该纪念品的销售单价定为多少元时,每星期销售这种产品获得的利润最大?最大利润是多少元?
19.陕西大樱桃发展十分迅速,后来居上,成为我国三大樱桃产地之一,其中,铜川大樱桃最为出名,先后荣获“国家地理标志保护产品”“中国优质甜樱桃之都”等殊荣,每到樱桃成熟的季节,就会有大批的水果商收购樱桃.今年某村在销售前对本地市场进行调查发现:当批发价为2.4万元/吨时,每天可售出13吨,每吨每涨0.2万元,每天的销量将减少1吨,据测算,每吨平均投入成本1万元,为了抢占市场,薄利多销,该村产业合作社决定,批发价不低于2.4万元/吨,不高于4.5万元/吨.设樱桃的批发价为x(万元/吨),每天获得的利润为y(万元),请解答下列问题:
(1)用含x的代数式表示每天樱桃的销售量为 (吨),并求出每天获得的利润y(万元)与批发价x(万元/吨)之间的函数关系式;
(2)若该村每天批发樱桃要盈利15万元,求樱桃的批发价应定为多少万元/吨?
(3)当樱桃的批发价定为多少万元时,每天所获的利润最大,并求出最大利润.
20.由于惯性的作用,行驶中的汽车在刹车后还要继续向前滑行一段距离才能停止,这段距离称为“刹车距离”.为了测定某种型号小型载客汽车的刹车性能(车速不超过140km/h),对这种型号的汽车进行了测试,测得的数据如下表:
刹车时车速v(km/h) 0 10 20 30 40 50 …
刹车距离s(m) 0 2.5 5 7.5 10 12.5 …
请回答下列问题:
(1)在这个变化过程中,自变量是 ,因变量是 .
(2)当刹车时车速为30km/h时,刹车距离是多少米?
(3)观察表中数据可知,当刹车时车速每增加10km/h时,刹车距离增加多少米?该型号汽车某次的刹车距离为20m,推测刹车时的车速是多少?
21.在某场篮球比赛中,运动员甲在距篮下7m的三分线外跳起投篮,球运行的路线大致是抛物线,当球运行的水平距离为4m时,球达到最大高度3.86m,然后准确落入篮圈,篮圈中心到地面的距离为3.05m,建立如图所示的平面直角坐标系.
(1)请求出该抛物线的表达式;
(2)另一运动员乙位于运动员甲与原点O之间,且距离甲为0.4m,原地起跳后成功盖帽拦截运动员甲投出的球,问:运动员乙起跳后双手达到的高度至少为多少?(结果精确到0.01m)
22.1~6个月的婴儿生长发育非常快,他们的体重y(g)和月龄x(月)的关系可以用y=a+700x来表示,其中a是婴儿出生时的体重.下面表格表示在1~6个月之间,这个婴儿的体重y与月龄x之间的关系.
月龄x/月 1 2 3 4 5 6
体重y/g 4200 4900 5600 6300 7000 7700
(1)上表反映的变化过程中, 是自变量, 是因变量;
(2)利用表中数据直接写出该婴儿体重y(g)和月龄x(月)之间的关系式为 ;
(3)若某婴儿出生时的体重为4000g,请计算该婴儿第6个月时体重是多少g?
应用题模型—建立函数模型解决实际问题 数学解题模型与方法
参考答案与试题解析
一.选择题(共8小题)
1.小明学习了物理中的欧姆定律发现:电阻两端的电压=电流强度×电流通过的电阻.已知某滑动变阻器两端电压恒定,当变阻器的电阻调节为10Ω时,测得通过该变阻器的电流为24A,则通过该滑动变阻器的电流I(单位:A)与电阻R(单位:Ω)之间的函数关系图象大致是( )
A. B.
C. D.
【答案】A
【解答】解:∵电阻两端的电压=电流强度×电流通过的电阻,
∴I=,
∵当R=10Ω时,I=24A,
∴=24,
∴U=240(V),
∴I=,
∴电流I与电阻R成反比例函数关系,
故答案A符合题意,
答案B是一次函数,故不符合题意,
答案C是正比例函数,故不符合题意,
答案D是二次函数,故不符合题意,
故选:A.
2.研究发现,近视镜的度数y(度)与镜片焦距x(米)成反比例函数关系,小明佩戴的400度近视镜片的焦距为0.25米,经过一段时间的矫正治疗加之注意用眼健康,现在镜片焦距为0.4米,则小明的近视镜度数可以调整为( )
A.500度 B.300度 C.250度 D.200度
【答案】C
【解答】解:设y=(k≠0),
∵x=0.25时,y=400,
∴,
∴k=100,
∴y与x的函数关系式为:y=,
当x=0.4时,y==250,
∴小明的近视镜度数可以调整为250度.
故选:C.
3.已知一个长方形的周长为50cm,相邻两边分别为xcm,ycm,则y与x之间的关系式为( )
A.y=50﹣x B.y=25﹣x C.y= D.y=
【答案】B
【解答】解:由题意得,2(x+y)=50,
解得y=25﹣x,
故选:B.
4.弹簧挂重物后会伸长,测得弹簧长度y(cm)量长为20cm,与所挂物体重量x(kg)间有下面的关系:下列说法不正确的是( )
x 0 1 2 3 4 …
y 8 8.5 9 9.5 10 …
A.x与y都是变量,x是自变量,y是因变量
B.所挂物体为6kg,弹簧长度为11cm
C.物体每增加1kg,弹簧长度就增加0.5cm
D.挂30kg物体时,弹簧长度一定比原长增加15cm
【答案】D
【解答】解:由题意可得,x与y都是变量,x是自变量,y是因变量,
∴选项A不符合题意;
由题意可得,在该弹簧弹性限度范围内所挂重物每增加1kg弹簧就多伸长0.5cm,则所挂物体为6kg,可计算得弹簧长度为11cm,挂30kg物体时,如果超出该弹簧的弹性限度范围,则弹簧长度就不会比原长增加15cm.
∴选项B、C不符合题意,选项D符合题意,
故选:D.
5.某科研小组在网上获取了声音在空气中传播的速度与空气温度关系的一些数据(如表):下列说法错误的是( )
温度/℃ ﹣20 ﹣10 0 10 20 30
声速/(m/s) 318 324 330 336 342 348
A.在这个变化中,自变量是温度,因变量是声速
B.温度越高,声速越快
C.当空气温度为20℃时,声音5s可以传播1740m
D.当温度每升高10℃,声速增加6m/s
【答案】C
【解答】解:由函数的定义可得,在这个变化中,自变量是温度,因变量是声速,
∴选项A不符合题意;
∵由表格信息可得,温度越高,声速越快,
∴选项B不符合题意;
∵当空气温度为20℃时,声音5s可以传播距离为342×20=1740(m),
∴选项C符合题意;
∵由题意得当温度每升高10℃,声速增加6m/s,
∴选项D不符合题意;
故选:C.
6.如图1,某地大桥主桥墩结构为抛物线形,桥墩的高度和宽度分别为40m和30m,若建立如图2所示的平面直角坐标系,则该抛物线的表达式为( )
A. B.y=30x2﹣40x
C. D.y=﹣40x2+30x
【答案】C
【解答】解:由二次函数的图象可得,抛物线与x轴的交点坐标为(0,0)和(30,0),
∴对称轴为x==15,
∵桥墩的高度为40m,
∴抛物线的顶点坐标为(15,40),
设抛物线的解析式为y=a(x﹣15)2+40(a≠0),
把(0,0)代入上式得,
a×152+40=0,
∴a=﹣,
∴该抛物线的表达式为y=﹣(x﹣15)2+40,
即y=﹣x2+x,
故选:C.
7.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,在△DEF中,DE=DF=5,EF=8,BC与EF在同一条直线上,点C与点E重合.△ABC以每秒1个单位长度的速度沿线段EF所在直线向右匀速运动,当点B运动到点F时,△ABC停止运动.设运动时间为t秒,△ABC与△DEF重叠部分的面积为S,则下列图象能大致反映S与t之间函数关系的是( )
A. B.
C. D.
【答案】A
【解答】解:过点D作DH⊥CB于H,
∵DE=DF=5,EF=8,
∴EH=FH=EF=4,
∴DH==3,
当0≤t<4时,
如图,重叠部分为△EPQ,此时EQ=t,PQ∥DH,
∴△EPQ∽△EDH,
∴,即,
∴PQ=t,
∴S==2,
当4≤t<8时,
如图,重叠部分为四边形POC′B′,此时BB′=CC′=t,PB∥DE.
∴B′F=BC+CF﹣BB′=12﹣t,FC=8﹣t,
∵PB∥DE,
∴△PBF∽△DCF,
∴,
又S△DCF=,
∴,
∵DH⊥BC.∠AB′C′=90°,
∴AC′∥DH,
∴△C′QF∽△HFD.
∴,即,
∴,
∴S=S△PB′F﹣S△C′QF==,
当8≤t≤12时
如图,重叠部分为四边形△PFB′,此时BB′=CC′=t,PB′∥DE.
∴B′F=BC+CF﹣BB′=12﹣t,
∵PB′∥DE.
∴△PB′F∽△DCF,
∴,即,
∴,S=S△PB′F=,
综上,
∴符合题意的函数图象是选项A.
故选:A.
8.台风影响着人们的生产和生活.人们为研究台风,将研究条件进行一定的合理简化,把近地面风速画在一个以台风中心为原点,以台风半径为横轴,风速为纵轴的坐标系中,并在图中标注了该台风的12级、10级和7级风圈半径,如12级风圈半径是指近地面风速衰减至32.7m/s时,离台风中心的距离约为150km.那么以下关于这场台风的说法中,正确的是( )
A.越靠近台风中心位置,风速越大
B.距台风中心150km处,风速达到最大值
C.10级风圈半径约为280km
D.在某个台风半径达到最大风速之后,随台风半径的增大,风速又逐渐衰减
【答案】D
【解答】解:A、根据图象可知,在图象的前段部分,风速随台风半径的增大而增大,则越靠近台风中心位置,风速越小(最小为10m/s),故A选项不符合题意;
B、根据图象可知,台风半径小于100km时,风速已达到最大值,故B选项不符合题意;
C、根据图象可知,10级风圈的台风半径为200km,风速为24.5m/s,故C选项不符合题意;
D、根据图象可知,风速先是随台风半径的增大而增大,风速达到最大之后,又随台风半径的增大而减小,故D选项符合题意.
故选:D.
二.填空题(共6小题)
9.密闭容器内有一定质量的二氧化碳,当容器的体积V(单位:m3)变化时,气体的密度ρ(单位:kg/m)随之变化.已知密度ρ与体积V是反比例函数关系,它的图象如图所示,当V=5m3时,ρ=1.98kg/m3.若3≤V≤9,二氧化碳密度ρ的变化范围 1.1≤ρ≤3.3 .
【答案】1.1≤ρ≤3.3.
【解答】解:∵密度ρ与体积V是反比例函数关系,
∴设,
∵当V=5m3时,ρ=1.98kg/m3,
∴,
∴k=1.98×5=9.9,
∴密度ρ关于体积V的函数解析式为:,
观察函数图象可知,ρ随V的增大而减小,
当V=3m3时,ρ==3.3(kg/m3),
当V=9m3时,ρ==1.1(kg/m3),
∴当3≤V≤9时,1.1≤ρ≤3.3(kg/m3),
即二氧化碳密度ρ的变化范围是1.1≤ρ≤3.3(kg/m3),
故答案为:1.1≤ρ≤3.3.
10.一支原长为20cm的蜡烛,点燃后,其剩余长度与燃烧时间的关系如表:
烧烧时间/分 10 20 30 40 50
剩余长度/cm 19 18 17 16 15
当这支蜡烛的剩余长度为10cm时,这支蜡烛燃烧了 100 分钟.
【答案】100.
【解答】解:设燃烧x分钟时该蜡烛的剩余长度为ycm,
由题意得该蜡烛每燃烧10分钟剩余长度减少1cm,
∴y=﹣x+20,
∴当y=10时,
﹣x+20=10,
解得x=100,
故答案为:100.
11.某超市购进一批拼装玩具,进价为每个10元,在销售过程中发现,日销售量y(个)与销售单价x(元)之间满足如图所示的一次函数关系,则该超市每天销售这款拼装玩具的最大利润为 800 元(利润=总销售额﹣总成本).
【答案】800.
【解答】解:设日销售量y与销售单价x之间的函数关系式为y=kx+b(k≠0),
∵点(25,50),(35,30)在函数图象上,
∴,
解得,
∴y=﹣2x+100,
设每天的销售利润为w元,
则w=(x﹣10) y
=(x﹣10)(﹣2x+100)
=﹣2x2+120x﹣1000
=﹣2(x﹣30)2+800,
∵﹣2<0,
∴开口向下,
∴当x=30时,w最大值=800,
即超市每天销售这款拼装玩具的最大利润为800元,
故答案为:800.
12.党的二十大报告指出:“高质量发展”是全面建设社会主义现代化的首要任务.在数学中,我们不妨设:在平面直角坐标系内,如果点(m,n)的坐标满足n=m2,那么称点(m,n)为“高质量发展点”.若点A(a,9)是反比例函数y=(k≠0)的图象上的“高质量发展点”,则该反比例函数的解析式为 y=或y=﹣ .
【答案】y=或y=﹣.
【解答】解:将(a,9)代入y=(k≠0)中得,=9,
∴k=9a,
∵点A(a,9)是“高质量发展点“,
∴a2=9,
解方程组得,
或,
则该反比例函数的解析式为y=或y=﹣.
13.为了预防“流感”,某学校对教室采用药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧完后,y与x成反比例(如图).现测得药物8min燃毕,此时室内空气中每立方米的含药量为6mg.研究表明,当空气中每立方米的含药量不低于3mg才有效,那么此次消毒的有效时间是 12 分钟.
【答案】12.
【解答】解:设药物燃烧时y与x的函数关系式为y=kx(k>0),
把(8,6)代入上式得,8k=6,
∴k=,
∴y=x(0≤x≤8);
设药物燃烧完后y与x的函数关系式为y=(k1>0),
把(8,6)代入上式得,=6,
∴k1=48,
∴y=(x>8),
当y=3时,x=3,x=4;=3,x=16,
∴此次消毒的有效时间为16﹣4=12(分钟),
故答案为:12.
14.已知矩形ABCD中,AB=2AD=8,点E、F分别是边AB、CD的中点,点P为AD边上动点,过点P作与AB平行的直线交AF于点G,连接PE,点M是PE中点,连接MG,则MG的最小值= .
【答案】.
【解答】解:方法一:如图,过点M作MN⊥PG于点N,取AP的中点H,连接MH,EF,
设AP=x,则AH=PH=x,
∵四边形ABCD是矩形,且AB=2AD=8,
∴AB=CD=8,AD=4,∠BAD=∠D=90°,AB∥CD,
∵PG∥AB,
∴PG∥CD,
∴∠APG=∠D=90°,
∵点E、F分别是边AB、CD的中点,AB=2AD=8,
∴AE=AD=DF=4,
∵点M是PE中点,点H是AP的中点,
∴MH∥AB,MH=AE=2,
∴∠PHM=∠BAD=90°,
∵MN⊥PG,
∴∠MNP=∠MNG=90°=∠PHM=∠APG,
∴四边形MNPH是矩形,
∴PN=MH=2,MN=PH=x,
∵AD=DF,∠D=90°,
∴△ADF是等腰直角三角形,
∴∠AFD=45°,
∵PG∥CD,
∴∠AGP=∠AFD=45°,
∵∠APG=90°,
∴△APG是等腰直角三角形,
∴PG=AP=x,
∴NG=PG﹣PN=x﹣2,
在Rt△MNG中,MG2=MN2+NG2=(x)2+(x﹣2)2=(x﹣)2+,
∵>0,
∴当x=时,MG2取得最小值,
∵MG===,
∴MG的最小值为,
故答案为:.
方法二:如图,以点D为原点,直线CD为x轴,直线AD为y轴建立平面直角坐标系,
∵四边形ABCD是矩形,且AB=2AD=8,
∴A(0,4),B(﹣8,4),C(﹣8,0),D(0,0),
∵点E、F分别是边AB、CD的中点,
∴E(﹣4,4),F(﹣4,0),
设P(0,t),
∵点M是PE中点,
∴M(﹣2,),
设直线AG的解析式为y=kx+b,则,
解得:,
∴直线AG的解析式为y=x+4,
∵PG∥x轴交AF于G,
∴G(t﹣4,t),
∴MG2=[(t﹣4)﹣(﹣2)]2+(t﹣)2=t2﹣6t+8=(t﹣)2+,
∵>0,
∴MG2有最小值,
∵MG>0,
∴MG的最小值为=,
故答案为:.
三.解答题(共9小题)
15.某医药研究所研制了一种新药,在试验药效时发现:成人按规定剂量服用后,检测到从第10分钟起每分钟每毫升血液中含药量增加0.3微克,第100分钟达到最高,接着开始衰退.血液中含药量y(微克)与时间x(分钟)的函数关系如图,并发现衰退时y与x成反比例函数关系.
(1)a= 27 ;
(2)分别求出当10≤x≤100和x>100时,y与x之间的函数关系式;
(3)如果每毫升血液中含药量不低于12微克时是有效的,求一次服药后的有效时间是多少分钟?
【答案】(1)27;
(2)当10≤x≤100时:y=0.3x﹣3,
当x>100时,y=;
(3)175分钟.
【解答】解:(1)∵从第10分钟起每分钟每毫升血液中含药量增加0.3微克,第100分钟达到最高,
∴a=(100﹣10)×0.3=27,
故答案为:27.
(2)当10≤x≤100时设y=kx+b,代入(10,0)和(100,27)得:
,
解得:,
∴当10≤x≤100时:y=0.3x﹣3,
当x>100时,设y=,代入(100,27),
∴m=100×27=2700,
当x>100时,y=;
(3)上升阶段药效达到12微克时间,
根据y=0.3x﹣3,
令y=12则12=0.3x﹣3,
解得:x=50分钟,
衰退阶段药效达到12微克时间,
由y=,
令y=12,则12=,
解得:x=225分钟,
∴一次服药后的有效时间是175分钟.
16.渠县是全国优质黄花主产地,某加工厂加工黄花的成本为30元/千克,根据市场调查发现,批发价定为48元/千克时,每天可销售500千克,为增大市场占有率,在保证盈利的情况下,工厂采取降价措施,批发价每千克降低1元,每天销量可增加50千克.
(1)设批发价每千克降x元,写出工厂每天的利润W元与降价x元之间的函数关系式.
(2)当降价多少元时,工厂每天的利润最大,最大为多少元?
(3)若工厂每天的利润要达到9750元,并让利于民,则定价应为多少元?
【答案】(1)W=﹣50x2+400x+9000;
(2)当降价4元时,工厂每天的利润最大,最大为9800元;
(3)定价应为43元.
【解答】解:(1)由题意得:
W=(48﹣30﹣x)(500+50x),
即W=﹣50x2﹣400x+9000
答:工厂每天的利润W元与降价x元之间的函数关系为W=﹣50x2+400x+9000;
(2)由(1)得:
W=﹣50x2+400x+9000=﹣50(x﹣4)2+9800
.﹣50<0,
.x=4时,W最大为9800,
即当降价4元时,工厂每天的利润最大,最大为9800元.
(3)﹣50x2+400x+9000=9750解得:x1=3,x2=5,
∵让利于民,
.x1=3不合题意,舍去,
定价应为48﹣5=43(元),
答:定价应为43元.
17.2022年北京冬奥会期间,某网店直接从工厂购进A、B两款冰墩墩钥匙扣,进货价和销售价如表:(注:利润=销售价﹣进货价)
类别 价格 A款钥匙扣 B款钥匙扣
进货价(元/件) 30 25
销售价(元/件) 45 37
(1)网店第一次用850元购进A、B两款钥匙扣共30件,求两款钥匙扣分别购进的件数;
(2)第一次购进的冰墩墩钥匙扣售完后,该网店计划再次购进A、B两款冰墩墩钥匙扣共80件(进货价和销售价都不变),且进货总价不高于2200元.应如何设计进货方案,才能获得最大销售利润,最大销售利润是多少?
【答案】(1)购进A款钥匙扣20件,B款钥匙扣10件.
(2)当购进40件A款钥匙扣,购进40件B款钥匙扣时,获得最大利润,最大利润为1080元.
【解答】解:(1)设购进A款钥匙扣x件,B款钥匙扣y件,
由题意得,,
解得,
答:购进A款钥匙扣20件,B款钥匙扣10件.
(2)设购进m件A款钥匙扣,则购进(80﹣m)件B款钥匙扣,
则30m+25(80﹣m)≤2200,
解得m≤40.
设再次购进后获得的总利润为w元,
则w=(45﹣30)m+(37﹣25)(80﹣m)=3m+960.
∵3>0,
∴w随m的增大而增大,
∴当m=40时,w最大值=3×40+960=1080,
此时80﹣m=40.
答:当购进40件A款钥匙扣,购进40件B款钥匙扣时,获得最大利润,最大利润为1080元.
18.某纪念品的进价为每件40元,售价为每件50元,每星期可卖出200个.经市场调查发现:以不低于现售价的价格销售该商品,售价每上涨1元,则每星期少卖4个(每件售价不高于68元),设每件商品销售单价为x(元),每星期销售量为y(个).
(1)求y与x之间的函数关系式,并直接写出自变量x的取值范围;
(2)将该纪念品的销售单价定为多少元时,每星期销售这种产品获得的利润最大?最大利润是多少元?
【答案】(1)y=﹣4x+400,50≤x≤68.
(2)单价定为68元时,每星期销售这种产品获得的利润最大,最大利润是3584元.
【解答】解:(1)由题意得:
y=200﹣4(x﹣50)
=﹣4x+400.
自变量x的取值范围为50≤x≤68.
(2)设每星期销售这种产品获得的利润为w元,
由题意得:
w=(x﹣40)(﹣4x+400)
=﹣4x2+560x﹣16000
=﹣4(x﹣70)2+3600,
∵a=﹣4<0,50≤x≤68,
∴当x=68时,w取得最大值,最大值为:﹣4(68﹣70)2+3600=3584,
答:单价定为68元时,每星期销售这种产品获得的利润最大,最大利润是3584元.
19.陕西大樱桃发展十分迅速,后来居上,成为我国三大樱桃产地之一,其中,铜川大樱桃最为出名,先后荣获“国家地理标志保护产品”“中国优质甜樱桃之都”等殊荣,每到樱桃成熟的季节,就会有大批的水果商收购樱桃.今年某村在销售前对本地市场进行调查发现:当批发价为2.4万元/吨时,每天可售出13吨,每吨每涨0.2万元,每天的销量将减少1吨,据测算,每吨平均投入成本1万元,为了抢占市场,薄利多销,该村产业合作社决定,批发价不低于2.4万元/吨,不高于4.5万元/吨.设樱桃的批发价为x(万元/吨),每天获得的利润为y(万元),请解答下列问题:
(1)用含x的代数式表示每天樱桃的销售量为 ﹣5x+25 (吨),并求出每天获得的利润y(万元)与批发价x(万元/吨)之间的函数关系式;
(2)若该村每天批发樱桃要盈利15万元,求樱桃的批发价应定为多少万元/吨?
(3)当樱桃的批发价定为多少万元时,每天所获的利润最大,并求出最大利润.
【答案】(1)﹣5x+25,y=﹣5x2+30x﹣25.
(2)4.
(3)当批发价定为3万元/吨时,每天获得的利润最大,最大利润是20万元.
【解答】解:(1)每天樱桃的销售量为13﹣=﹣5x+25(吨),
根据题意得,y=(﹣5x+25)(x﹣1)=﹣5x2+30x﹣25,
∴每天获得的利润y(万元)与批发价x(万元/吨)之间的函数关系式为y=﹣5x2+30x﹣25.
故答案为:﹣5x+25.
(2)根据题意可得﹣5x2+30x﹣25=15,
解得x1=2,x2=4,
∵2.4≤x≤4.5,
∴x=4,
答:若该村每天批发樱桃要盈利15万元,樱桃的批发价应定为4万元/吨.
(3)y=﹣5x2+30x﹣25=﹣5(x﹣3)2+20,
∵2.4≤x≤4.5,
∴当x=3时,y有最大值,y最大值=20,
∴当批发价定为3万元/吨时,每天获得的利润最大,最大利润是20万元.
20.由于惯性的作用,行驶中的汽车在刹车后还要继续向前滑行一段距离才能停止,这段距离称为“刹车距离”.为了测定某种型号小型载客汽车的刹车性能(车速不超过140km/h),对这种型号的汽车进行了测试,测得的数据如下表:
刹车时车速v(km/h) 0 10 20 30 40 50 …
刹车距离s(m) 0 2.5 5 7.5 10 12.5 …
请回答下列问题:
(1)在这个变化过程中,自变量是 刹车时车速v ,因变量是 刹车距离s .
(2)当刹车时车速为30km/h时,刹车距离是多少米?
(3)观察表中数据可知,当刹车时车速每增加10km/h时,刹车距离增加多少米?该型号汽车某次的刹车距离为20m,推测刹车时的车速是多少?
【答案】(1)刹车时车速v,刹车距离s;
(2)当刹车时车速为30km/h时,刹车距离是7.5米;
(3)当刹车时车速每增加10km/h时,刹车距离增加2.5米;当该型号汽车某次的刹车距离为20m时,刹车时的车速是80km/h.
【解答】解:(1)由题意得,
在这个变化过程中,自变量是刹车时车速v,因变量是刹车距离s,
故答案为:刹车时车速v,刹车距离s;
(2)由题意得,当刹车时车速为30km/h时,刹车距离是7.5米,
答:当刹车时车速为30km/h时,刹车距离是7.5米;
(3)由表中数据可知,当刹车时车速每增加10km/h时,刹车距离增加2.5米,
∴刹车距离s和刹车时车速v间的函数关系式为:s=v,
整理,得s=0.25v,
由题意可得0.25v=20,
解得v=80,
答:当刹车时车速每增加10km/h时,刹车距离增加2.5米;当该型号汽车某次的刹车距离为20m时,刹车时的车速是80km/h.
21.在某场篮球比赛中,运动员甲在距篮下7m的三分线外跳起投篮,球运行的路线大致是抛物线,当球运行的水平距离为4m时,球达到最大高度3.86m,然后准确落入篮圈,篮圈中心到地面的距离为3.05m,建立如图所示的平面直角坐标系.
(1)请求出该抛物线的表达式;
(2)另一运动员乙位于运动员甲与原点O之间,且距离甲为0.4m,原地起跳后成功盖帽拦截运动员甲投出的球,问:运动员乙起跳后双手达到的高度至少为多少?(结果精确到0.01m)
【答案】(1)y=﹣0.09x2+3.86.
(2)2.69米.
【解答】解:(1)由于球运行的水平距离为4m时,球达到最大高度3.86m,
则设该抛物线的表达式为y=ax2+3.86(a≠0),
代入(3,3.05)得,9a+3.86=3.05,
解得a=﹣0.09,
∴该抛物线的表达式为y=﹣0.09x2+3.86.
(2)∵4﹣0.4=3.6,
∴运动员乙所在位置的横坐标为﹣3.6,
当x=﹣3.6时,y=﹣0.09×(﹣3.6)2+3.86≈2.69,
答:运动员乙起跳后双手达到的高度至少为2.69米.
22.1~6个月的婴儿生长发育非常快,他们的体重y(g)和月龄x(月)的关系可以用y=a+700x来表示,其中a是婴儿出生时的体重.下面表格表示在1~6个月之间,这个婴儿的体重y与月龄x之间的关系.
月龄x/月 1 2 3 4 5 6
体重y/g 4200 4900 5600 6300 7000 7700
(1)上表反映的变化过程中, 月龄x 是自变量, 体重y 是因变量;
(2)利用表中数据直接写出该婴儿体重y(g)和月龄x(月)之间的关系式为 y=700x+3500 ;
(3)若某婴儿出生时的体重为4000g,请计算该婴儿第6个月时体重是多少g?
【答案】(1)月龄x;体重y
(2)y=700x+3500;
(3)该婴儿第6个月时体重是8200g.
【解答】解:(1)由题意得,
上表反映的变化过程中,月龄x是自变量,体重y是因变量,
故答案为:月龄x,体重y;
(2)由题意得,
a+700×1=4200,
解得a=3500,
利用表中数据直接写出该婴儿体重y(g)和月龄x(月)之间的关系式为:y=700x+3500,
故答案为:y=700x+3500;
(3)若出生时体重为4000g,则体重和月龄之间的关系为:y=4000+700x
当x=6时,y=4000+700×6=8200(g),
答:该婴儿第6个月时体重是8200g.
同课章节目录
