2023—2024学年人教版数学九年级上册第25章概率初步 单元达标测试题(含解析)
文档属性
| 名称 | 2023—2024学年人教版数学九年级上册第25章概率初步 单元达标测试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 300.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-14 12:34:11 | ||
图片预览




文档简介
2023-2024学年第一学期人教版九年级数学《第25章概率初步》
单元达标测试题(附答案)
一、单选题(满分32分)
1.下列事件中,是确定事件的是( )
A.掷一枚硬币,正面朝上 B.三角形的内角和是
C.明天会下雨 D.明天的数学测验,小明会得满分
2.在4张完全相同的卡片上分别写上数字2,3,4,5,从中任意抽取两张.所得两个数字组成的两位数是3的倍数的是概率是( )
A. B. C. D.
3.下列随机事件的概率等于的是( )
A.一副普通扑克牌洗匀后,从中任取一张牌的花色是红桃
B.从一个装有个白球和个红球的袋子中任取球,取到白球
C.任意转动一个黑、白各占一半的圆形转盘,指针指向白色
D.掷一个质地均匀的正六面体骰子,向上的面点数是的倍数
4.已知变量x,y满足函数关系.现有牌面数字为3,,0,2的卡片,它们除数字外完全相同.把卡片背面朝上洗匀,然后从中随机抽取两张,则这两张卡片上所标的数字积为k的值,能使上述函数中y的值随x值的增大而增大的概率为( )
A. B. C. D.
5.柜子里放着张明和爸爸的两双不同的鞋,如果张明从中随机地取出2只,那么取出的鞋恰好是张明的鞋的概率为( )
A. B. C. D.
6.如图,随机闭合4个开关,,,中的两个开关,能使小灯泡L发光的概率是( )
A. B. C. D.
7.如图,分别旋转两个转盘,转出的两个数字之积为6的概率是( )
A. B. C. D.
8.下表是某种幼苗在一定条件下移植后成活率的试验结果:
移植总数n 5 50 200 500 1000 3000
成活数m 4 45 188 476 951 285
成活的频率 0.8 0.9 0.94 0.952 0.951 0.95
则在相同条件下这种幼苗成活的概率(精确到百分位)估计为( )
A.0.95 B.0.94 C.0.9 D.0.951
二、填空题(满分32分)
9.在0,,1.333…,,3.14,中,随机选取一个数,是无理数的概率是 .
10.在一个不透明的口袋中装有2个红球、2个黑球,这些球除颜色外其他都相同,随机地从这个袋子中一次摸出两个球,则摸到两个球都是红球的概率是 .
11.口袋中有红、黄、绿三种颜色的球,这些球除颜色外完全相同,其中红球有8个,绿球有10个,从中任意摸出一个球是绿色的概率为,则任意摸出一个球是黄球的概率为 .
12.在一个不透明的口袋里装有除颜色外其它均相同的白球2个,黄球1个,红球1个,第一次任意摸出一个球不放回,第二次再摸出一个球,则两次摸到的都是白球的概率为 .
13.如图,一块游戏板由大小相等的小正方形格子构成,若某游戏者随机向游戏板投掷一枚飞镖,那么飞镖击中阴影区域的概率是 .
14.木箱里装有白色卡片若干张,在不允许将卡片倒出来的情况下,为了估计其数量,小强将5张黑色卡片放入木箱,搅匀后随机摸出一张卡片记下颜色,再放回木箱中,经过多次重复试验,发现摸到黑色卡片的频率稳定在0.2附近,则木箱中大约有白色卡片 张.
15.在一个不透明的袋子里装有红球、黄球共20个,这些球除颜色外都相同.小明通过多次试验发现,摸出红球的频率稳定在0.4左右,则袋子中红球的大约有 个.
16.河南某地中招体育考试项目采取统一考试的方式进行,项目为“两个必考项目+两个抽签考试项目”,抽答项目分为技能类(包含足球和篮球)和素质举(包括立定跳远和一分钟绳),抽签项目“摇号产生”(从技能类和素质类中各随机抽取一个),抽中“足球和立定跳远”的概率为 .
三、解答题(满分56分)
17.为阻断流感传播,某社区设置了三个发热检测点,假定甲、乙两人去某个检测点是随机的,且去每个检测点机会均等.
(1)甲在A检测点的概率为________;
(2)求甲、乙两人在不同检测点的概率.
18.根据党中央对“精准扶贫,科教扶贫”的要求,某校将选派名教师去贫困山区学校支教,现有刘老师、王老师、张老师、李老师符合条件报名参加,学校决定从这位老师中任意选派名前往.
(1)“赵老师被选派”是______事件,“王老师被选派”是______事件(填“不可能”或“必然”或“随机”).
(2)用画树状图或列表的方法表示这次选派所有可能的结果,并求出“王老师被选派”的概率.
19.为拓展学生的视野,某校准备组织四个课题活动,课题1—5G的发展前景;课题2—航空航天宇宙探索;课题3—传统优秀文化传承;课题4——网络信息筛选.由于课题活动时间重叠,每位同学只能选择一个课题,晓含和小婷两人决定采用抽签的方式确定课题的主题,四支签上分别写有四个课题的名称,晓含从这四支签中随机抽取一支,不放回,小婷再从剩下的三支签中随机抽取一支.
(1)晓含抽到课题1的概率是______;
(2)请用列表或画树状图的方法求晓含和小婷中有一人抽到课题3的概率.
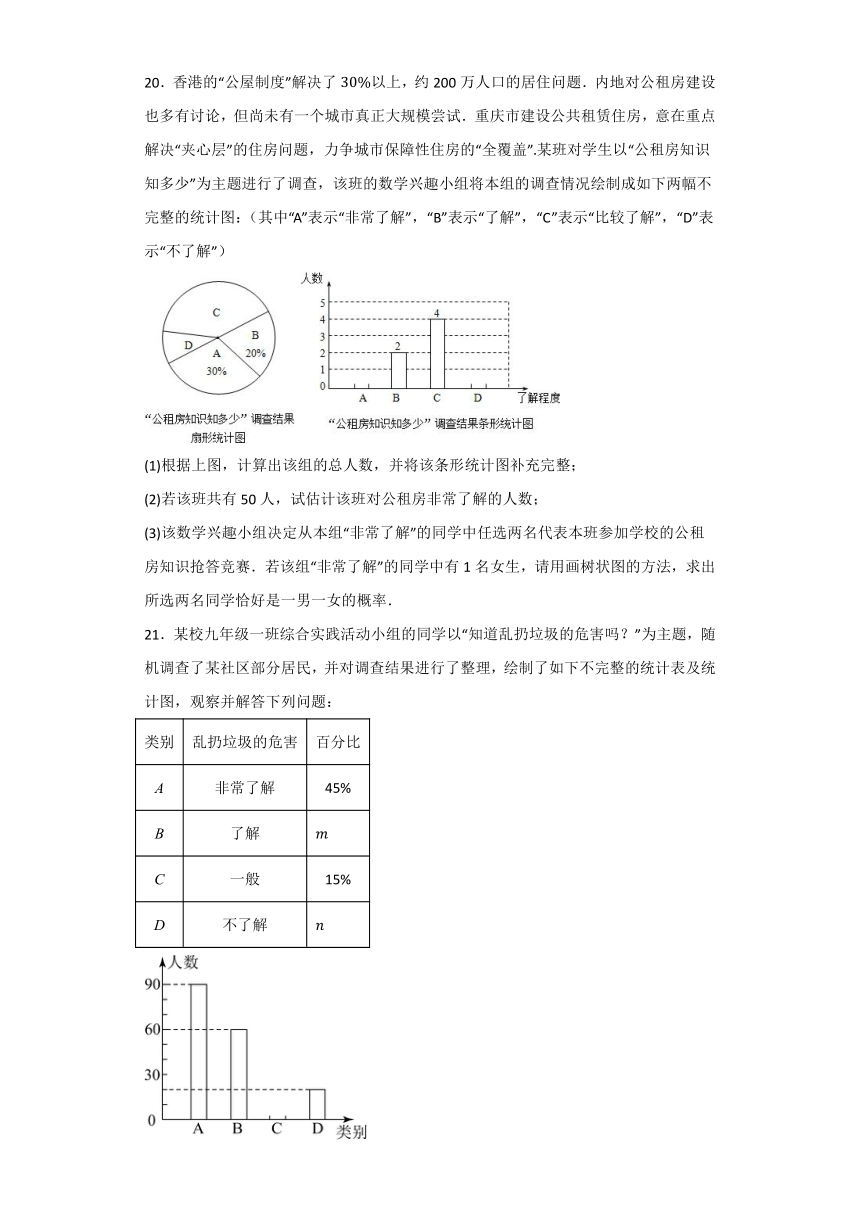
20.香港的“公屋制度”解决了以上,约200万人口的居住问题.内地对公租房建设也多有讨论,但尚未有一个城市真正大规模尝试.重庆市建设公共租赁住房,意在重点解决“夹心层”的住房问题,力争城市保障性住房的“全覆盖”某班对学生以“公租房知识知多少”为主题进行了调查,该班的数学兴趣小组将本组的调查情况绘制成如下两幅不完整的统计图:(其中“A”表示“非常了解”,“B”表示“了解”,“C”表示“比较了解”,“D”表示“不了解”)
(1)根据上图,计算出该组的总人数,并将该条形统计图补充完整;
(2)若该班共有50人,试估计该班对公租房非常了解的人数;
(3)该数学兴趣小组决定从本组“非常了解”的同学中任选两名代表本班参加学校的公租房知识抢答竞赛.若该组“非常了解”的同学中有1名女生,请用画树状图的方法,求出所选两名同学恰好是一男一女的概率.
21.某校九年级一班综合实践活动小组的同学以“知道乱扔垃圾的危害吗?”为主题,随机调查了某社区部分居民,并对调查结果进行了整理,绘制了如下不完整的统计表及统计图,观察并解答下列问题:
类别 乱扔垃圾的危害 百分比
A 非常了解 45%
B 了解
C 一般 15%
D 不了解
(1)求本次被调查居民的人数及m,n的值,并补全条形统计图;
(2)若该社区有1600人口,估计B,C两类居民共有多少人?
(3)小明同学在四个质地、大小、形状都完全相同的小球标记上A,B,C,D(代表乱扔垃圾的危害知道情况),并放在一个不透明的盒子中,他先随机抽取一个小球,放回去,再随机抽取一个小球,请用画树状图或列表的方法,求小明同学刚好抽到B和D的概率.
参考答案
1.解:A、掷一枚硬币,正面朝上,是随机事件,故不符合题意;
B、三角形的内角和是,是必然事件,属于确定事件,故符合题意;
C、明天会下雨为随机事件,故不符合题意;
D、明天的数学测验,小明会得满分为随机事件,故不符合题意,
故选:B.
2.解:画树状图如下:
共有12种等可能的结果,其中所得两个数字组成的两位数是3的倍数的结果有:24,42,45,54,共4种,
所得两个数字组成的两位数是3的倍数的概率为.
故选:.
3.解: A、一副普通扑克牌洗匀后,从中任取一张牌的花色是红桃的概率为,故不符合题意;
B、从一个装有个白球和个红球的袋子中任取球,取到白球的概率为,不符合题意;
C、任意转动一个黑、白各占一半的圆形转盘,指针指向白色的概率为,不符合题意;
D、掷一个质地均匀的正六面体骰子,向上的面点数是的倍数的概率为,故符合题意;
故选: D.
4.解:要使函数中y的值随x值的增大而增大,则,
画树状图如下:
由树状图可知一共有12种等可能性的结果数,其中能使上述函数中y的值随x值的增大而增大的结果数有2,
∴上述函数中y的值随x值的增大而增大的概率为,
故选A.
5.解:设两双鞋的型号分别为:,
其中是张明的一双鞋,是爸爸的一双鞋,
画树状图如下:
共有12种等可能的结果,取出的鞋是张明的鞋有2种,
则取出的鞋是张明的鞋的概率为:,
故选:D.
6.解:画树状图如下:
共有12种等可能的结果,其中能使小灯泡L发光的结果有:,共8种,
∴能使小灯泡L发光的概率为.
故选:A.
7.解:列表如下:
2 3
2 4 6
3 6 9
由表可得:所有可能的结果数有4种,积为6的情况数有2种,
∴旋转两个转盘,转出的两个数字之积为6的概率是;
故选A
8.解:∵成活的频率的稳定值约为0.95,
∴这种幼苗可成活的概率可估计为0.95,
故选A.
9.解:选取一个数有6种可能,其中是无理数的有两种,即,,所以概率为:,
故答案为:.
10.解:按照题意列表如下:
红1 红2 黑1 黑2
红1 红2红1 黑1红1 黑2红1
红2 红1红2 黑1红2 黑2红2
黑1 红1黑1 红2黑1 黑2黑1
黑2 红1黑2 红2黑2 黑1黑2
共有12种可能,其中两个球都是红球的有两种情况,
P(两个球都是红球).
故答案为:.
11.解:设有x个黄球,
根据题意,得,
解得:(经检验,符合题意),
即口袋中黄球有个;
袋子中共有个小球,其中黄球有个,
任意摸出一个球是黄球的概率为
故答案为:.
12.解:树状图如图所示,
如图表示所有可能的情况,共有12种等可能的结果,而二次都摸到白球的结果有2次,
可知其概率为,
故答案为.
13.解:图中阴影部分面积为,
游戏板面积为,
∴飞镖击中阴影区域的概率是.
故答案为:.
14.解:设木箱中白色卡片有x个,根据题意得:
,
解得:,
经检验是原方程的解,
则估计木箱中白色卡片有20张.
故答案为:20.
15.解:∵红球的频率稳定在0.4左右,
∴摸出红球的概率为0.4,
由概率公式得红球个数为,
故答案为:8.
16.解:用“A”、“B”分别表示足球和篮球项目,用“甲”、“乙”分别表示立定跳远和一分钟绳,列表如下:
技能类 素质类 甲 乙
A A甲 A乙
B B甲 B乙
则总的情况有4种,结果为“足球和立定跳远”的情况只有1种,
故抽中“足球和立定跳远”的概率为,
故答案为:.
17.(1)解:甲在A检测点的概率为,
故答案为:;
(2)画树状图如下:
共有种等可能的结果,其中甲、乙两人在不同检测点做核酸有种结果,
∴甲、乙两人在不同检测点的概率为.
18.(1)解:由题意知,“赵老师被选派”是不可能事件,“王老师被选派”是随机事件,
故答案为:不可能,随机;
(2)解:用姓氏代表该姓氏老师,由题意列表格如下:
刘 王 张 李
刘 (刘,王) (刘,张) (刘,李)
王 (王,刘) (王,张) (王,李)
张 (张,刘) (张,王) (张,李)
李 (李,刘) (李,王) (李,张)
∴由表格可知,共有12种等可能的选派方式,其中王老师被选派共有6种等可能的选派方式,
∵,
∴“王老师被选派”的概率为.
19.(1)解:四个课题活动,晓含抽到课题1的概率是,
故答案为:.
(2)解:列表如下,
晓含 小婷 课题1 课题2 课题3 课题4
课题1 课题1,课题2 课题1,课题3 课题1,课题4
课题2 课题2,课题1 课题2,课题3 课题2,课题4
课题3 课题3,课题1 课题3,课题2 课题3,课题4
课题4 课题4,课题1 课题4,课题2 课题4,课题3
共有12种等可能结果,符合题意的有6种,
∴晓含和小婷中有一人抽到课题3的概率为.
20.解:(1)该组的总人数人,
A的人数:(人),
D的人数为:,
补图如下:
(2)(人),
答:估计该班对公租房非常了解的人数约为15人;
(3)画树状图如下:
共有6种情况,每种情况可能性相等,所选两名同学恰好是一男一女有4种情况,
所以,所选两名同学恰好是一男一女.
21.(1)解:本次被调查居民的总人数为:(人);
,
;
C类人数为:(人),
补全条形统计图为:
;
(2)解:,
所以估计B,C两类居民共有720人;
(3)解:画树状图为:
共有16种等可能的结果数,其中小明同学刚好抽到B和D的结果数为2,
所以小明同学刚好抽到B和D的概率.
单元达标测试题(附答案)
一、单选题(满分32分)
1.下列事件中,是确定事件的是( )
A.掷一枚硬币,正面朝上 B.三角形的内角和是
C.明天会下雨 D.明天的数学测验,小明会得满分
2.在4张完全相同的卡片上分别写上数字2,3,4,5,从中任意抽取两张.所得两个数字组成的两位数是3的倍数的是概率是( )
A. B. C. D.
3.下列随机事件的概率等于的是( )
A.一副普通扑克牌洗匀后,从中任取一张牌的花色是红桃
B.从一个装有个白球和个红球的袋子中任取球,取到白球
C.任意转动一个黑、白各占一半的圆形转盘,指针指向白色
D.掷一个质地均匀的正六面体骰子,向上的面点数是的倍数
4.已知变量x,y满足函数关系.现有牌面数字为3,,0,2的卡片,它们除数字外完全相同.把卡片背面朝上洗匀,然后从中随机抽取两张,则这两张卡片上所标的数字积为k的值,能使上述函数中y的值随x值的增大而增大的概率为( )
A. B. C. D.
5.柜子里放着张明和爸爸的两双不同的鞋,如果张明从中随机地取出2只,那么取出的鞋恰好是张明的鞋的概率为( )
A. B. C. D.
6.如图,随机闭合4个开关,,,中的两个开关,能使小灯泡L发光的概率是( )
A. B. C. D.
7.如图,分别旋转两个转盘,转出的两个数字之积为6的概率是( )
A. B. C. D.
8.下表是某种幼苗在一定条件下移植后成活率的试验结果:
移植总数n 5 50 200 500 1000 3000
成活数m 4 45 188 476 951 285
成活的频率 0.8 0.9 0.94 0.952 0.951 0.95
则在相同条件下这种幼苗成活的概率(精确到百分位)估计为( )
A.0.95 B.0.94 C.0.9 D.0.951
二、填空题(满分32分)
9.在0,,1.333…,,3.14,中,随机选取一个数,是无理数的概率是 .
10.在一个不透明的口袋中装有2个红球、2个黑球,这些球除颜色外其他都相同,随机地从这个袋子中一次摸出两个球,则摸到两个球都是红球的概率是 .
11.口袋中有红、黄、绿三种颜色的球,这些球除颜色外完全相同,其中红球有8个,绿球有10个,从中任意摸出一个球是绿色的概率为,则任意摸出一个球是黄球的概率为 .
12.在一个不透明的口袋里装有除颜色外其它均相同的白球2个,黄球1个,红球1个,第一次任意摸出一个球不放回,第二次再摸出一个球,则两次摸到的都是白球的概率为 .
13.如图,一块游戏板由大小相等的小正方形格子构成,若某游戏者随机向游戏板投掷一枚飞镖,那么飞镖击中阴影区域的概率是 .
14.木箱里装有白色卡片若干张,在不允许将卡片倒出来的情况下,为了估计其数量,小强将5张黑色卡片放入木箱,搅匀后随机摸出一张卡片记下颜色,再放回木箱中,经过多次重复试验,发现摸到黑色卡片的频率稳定在0.2附近,则木箱中大约有白色卡片 张.
15.在一个不透明的袋子里装有红球、黄球共20个,这些球除颜色外都相同.小明通过多次试验发现,摸出红球的频率稳定在0.4左右,则袋子中红球的大约有 个.
16.河南某地中招体育考试项目采取统一考试的方式进行,项目为“两个必考项目+两个抽签考试项目”,抽答项目分为技能类(包含足球和篮球)和素质举(包括立定跳远和一分钟绳),抽签项目“摇号产生”(从技能类和素质类中各随机抽取一个),抽中“足球和立定跳远”的概率为 .
三、解答题(满分56分)
17.为阻断流感传播,某社区设置了三个发热检测点,假定甲、乙两人去某个检测点是随机的,且去每个检测点机会均等.
(1)甲在A检测点的概率为________;
(2)求甲、乙两人在不同检测点的概率.
18.根据党中央对“精准扶贫,科教扶贫”的要求,某校将选派名教师去贫困山区学校支教,现有刘老师、王老师、张老师、李老师符合条件报名参加,学校决定从这位老师中任意选派名前往.
(1)“赵老师被选派”是______事件,“王老师被选派”是______事件(填“不可能”或“必然”或“随机”).
(2)用画树状图或列表的方法表示这次选派所有可能的结果,并求出“王老师被选派”的概率.
19.为拓展学生的视野,某校准备组织四个课题活动,课题1—5G的发展前景;课题2—航空航天宇宙探索;课题3—传统优秀文化传承;课题4——网络信息筛选.由于课题活动时间重叠,每位同学只能选择一个课题,晓含和小婷两人决定采用抽签的方式确定课题的主题,四支签上分别写有四个课题的名称,晓含从这四支签中随机抽取一支,不放回,小婷再从剩下的三支签中随机抽取一支.
(1)晓含抽到课题1的概率是______;
(2)请用列表或画树状图的方法求晓含和小婷中有一人抽到课题3的概率.
20.香港的“公屋制度”解决了以上,约200万人口的居住问题.内地对公租房建设也多有讨论,但尚未有一个城市真正大规模尝试.重庆市建设公共租赁住房,意在重点解决“夹心层”的住房问题,力争城市保障性住房的“全覆盖”某班对学生以“公租房知识知多少”为主题进行了调查,该班的数学兴趣小组将本组的调查情况绘制成如下两幅不完整的统计图:(其中“A”表示“非常了解”,“B”表示“了解”,“C”表示“比较了解”,“D”表示“不了解”)
(1)根据上图,计算出该组的总人数,并将该条形统计图补充完整;
(2)若该班共有50人,试估计该班对公租房非常了解的人数;
(3)该数学兴趣小组决定从本组“非常了解”的同学中任选两名代表本班参加学校的公租房知识抢答竞赛.若该组“非常了解”的同学中有1名女生,请用画树状图的方法,求出所选两名同学恰好是一男一女的概率.
21.某校九年级一班综合实践活动小组的同学以“知道乱扔垃圾的危害吗?”为主题,随机调查了某社区部分居民,并对调查结果进行了整理,绘制了如下不完整的统计表及统计图,观察并解答下列问题:
类别 乱扔垃圾的危害 百分比
A 非常了解 45%
B 了解
C 一般 15%
D 不了解
(1)求本次被调查居民的人数及m,n的值,并补全条形统计图;
(2)若该社区有1600人口,估计B,C两类居民共有多少人?
(3)小明同学在四个质地、大小、形状都完全相同的小球标记上A,B,C,D(代表乱扔垃圾的危害知道情况),并放在一个不透明的盒子中,他先随机抽取一个小球,放回去,再随机抽取一个小球,请用画树状图或列表的方法,求小明同学刚好抽到B和D的概率.
参考答案
1.解:A、掷一枚硬币,正面朝上,是随机事件,故不符合题意;
B、三角形的内角和是,是必然事件,属于确定事件,故符合题意;
C、明天会下雨为随机事件,故不符合题意;
D、明天的数学测验,小明会得满分为随机事件,故不符合题意,
故选:B.
2.解:画树状图如下:
共有12种等可能的结果,其中所得两个数字组成的两位数是3的倍数的结果有:24,42,45,54,共4种,
所得两个数字组成的两位数是3的倍数的概率为.
故选:.
3.解: A、一副普通扑克牌洗匀后,从中任取一张牌的花色是红桃的概率为,故不符合题意;
B、从一个装有个白球和个红球的袋子中任取球,取到白球的概率为,不符合题意;
C、任意转动一个黑、白各占一半的圆形转盘,指针指向白色的概率为,不符合题意;
D、掷一个质地均匀的正六面体骰子,向上的面点数是的倍数的概率为,故符合题意;
故选: D.
4.解:要使函数中y的值随x值的增大而增大,则,
画树状图如下:
由树状图可知一共有12种等可能性的结果数,其中能使上述函数中y的值随x值的增大而增大的结果数有2,
∴上述函数中y的值随x值的增大而增大的概率为,
故选A.
5.解:设两双鞋的型号分别为:,
其中是张明的一双鞋,是爸爸的一双鞋,
画树状图如下:
共有12种等可能的结果,取出的鞋是张明的鞋有2种,
则取出的鞋是张明的鞋的概率为:,
故选:D.
6.解:画树状图如下:
共有12种等可能的结果,其中能使小灯泡L发光的结果有:,共8种,
∴能使小灯泡L发光的概率为.
故选:A.
7.解:列表如下:
2 3
2 4 6
3 6 9
由表可得:所有可能的结果数有4种,积为6的情况数有2种,
∴旋转两个转盘,转出的两个数字之积为6的概率是;
故选A
8.解:∵成活的频率的稳定值约为0.95,
∴这种幼苗可成活的概率可估计为0.95,
故选A.
9.解:选取一个数有6种可能,其中是无理数的有两种,即,,所以概率为:,
故答案为:.
10.解:按照题意列表如下:
红1 红2 黑1 黑2
红1 红2红1 黑1红1 黑2红1
红2 红1红2 黑1红2 黑2红2
黑1 红1黑1 红2黑1 黑2黑1
黑2 红1黑2 红2黑2 黑1黑2
共有12种可能,其中两个球都是红球的有两种情况,
P(两个球都是红球).
故答案为:.
11.解:设有x个黄球,
根据题意,得,
解得:(经检验,符合题意),
即口袋中黄球有个;
袋子中共有个小球,其中黄球有个,
任意摸出一个球是黄球的概率为
故答案为:.
12.解:树状图如图所示,
如图表示所有可能的情况,共有12种等可能的结果,而二次都摸到白球的结果有2次,
可知其概率为,
故答案为.
13.解:图中阴影部分面积为,
游戏板面积为,
∴飞镖击中阴影区域的概率是.
故答案为:.
14.解:设木箱中白色卡片有x个,根据题意得:
,
解得:,
经检验是原方程的解,
则估计木箱中白色卡片有20张.
故答案为:20.
15.解:∵红球的频率稳定在0.4左右,
∴摸出红球的概率为0.4,
由概率公式得红球个数为,
故答案为:8.
16.解:用“A”、“B”分别表示足球和篮球项目,用“甲”、“乙”分别表示立定跳远和一分钟绳,列表如下:
技能类 素质类 甲 乙
A A甲 A乙
B B甲 B乙
则总的情况有4种,结果为“足球和立定跳远”的情况只有1种,
故抽中“足球和立定跳远”的概率为,
故答案为:.
17.(1)解:甲在A检测点的概率为,
故答案为:;
(2)画树状图如下:
共有种等可能的结果,其中甲、乙两人在不同检测点做核酸有种结果,
∴甲、乙两人在不同检测点的概率为.
18.(1)解:由题意知,“赵老师被选派”是不可能事件,“王老师被选派”是随机事件,
故答案为:不可能,随机;
(2)解:用姓氏代表该姓氏老师,由题意列表格如下:
刘 王 张 李
刘 (刘,王) (刘,张) (刘,李)
王 (王,刘) (王,张) (王,李)
张 (张,刘) (张,王) (张,李)
李 (李,刘) (李,王) (李,张)
∴由表格可知,共有12种等可能的选派方式,其中王老师被选派共有6种等可能的选派方式,
∵,
∴“王老师被选派”的概率为.
19.(1)解:四个课题活动,晓含抽到课题1的概率是,
故答案为:.
(2)解:列表如下,
晓含 小婷 课题1 课题2 课题3 课题4
课题1 课题1,课题2 课题1,课题3 课题1,课题4
课题2 课题2,课题1 课题2,课题3 课题2,课题4
课题3 课题3,课题1 课题3,课题2 课题3,课题4
课题4 课题4,课题1 课题4,课题2 课题4,课题3
共有12种等可能结果,符合题意的有6种,
∴晓含和小婷中有一人抽到课题3的概率为.
20.解:(1)该组的总人数人,
A的人数:(人),
D的人数为:,
补图如下:
(2)(人),
答:估计该班对公租房非常了解的人数约为15人;
(3)画树状图如下:
共有6种情况,每种情况可能性相等,所选两名同学恰好是一男一女有4种情况,
所以,所选两名同学恰好是一男一女.
21.(1)解:本次被调查居民的总人数为:(人);
,
;
C类人数为:(人),
补全条形统计图为:
;
(2)解:,
所以估计B,C两类居民共有720人;
(3)解:画树状图为:
共有16种等可能的结果数,其中小明同学刚好抽到B和D的结果数为2,
所以小明同学刚好抽到B和D的概率.
同课章节目录
