2023-2024学年高一物理人教版必修一2.3. 匀变速直线运动的位移与时间的关系同步练习(含解析)
文档属性
| 名称 | 2023-2024学年高一物理人教版必修一2.3. 匀变速直线运动的位移与时间的关系同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 255.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-08-13 09:58:23 | ||
图片预览




文档简介
3. 匀变速直线运动的位移与时间的关系
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1. 一物体做匀变速直线运动,下列说法中正确的是( )
A. 物体的末速度一定与时间成正比
B. 物体的位移一定与时间的平方成正比
C. 物体的速度在一定时间内发生的变化与这段时间成正比
D. 若为匀加速运动,速度和位移都随时间增加;若为匀减速运动,速度和位移都随时间减小
2. 如图所示是物体运动的图像,从开始,物体位移最大的时刻是 ( )
A. B. C. D.
3. 一物体从斜面上某点由静止开始做匀加速直线运动,经过到达斜面底端,并开始在水平地面上做匀减速直线运动,经过停止。设物体由斜面底端运动到水平地面上时速度大小不变,则物体在斜面上的位移大小与在水平地面上的位移大小之比是( )
A. B. C. D.
4. “道路千万条,安全第一条”,一辆汽车在平直公路上以的速度匀速行驶,驾驶员发现前方处的斑马线上有行人,驾驶员立即刹车使汽车做匀减速直线运动并最终停在斑马线之前,则刹车后汽车的加速度大小至少为( )
A. B. C. D.
5. 一汽车从静止开始做匀加速直线运动,然后刹车做匀减速直线运动,直到停止.下列速度和位移的关系图像中,能描述该过程的是 ( )
A. B. C. D.
6. 汽车在水平路面上刹车,其位移与时间的关系是,则它在前内的位移是 ( )
A. B. C. D.
7. 一质点在连续的内做匀加速直线运动,在第一个内位移为,第二个内位移为,下面说法正确的是( )
A. 质点在第末的速度大小为 B. 质点在第末的速度大小为
C. 质点的加速度大小为 D. 质点在内的平均速度大小为
8. 一辆汽车从静止开始由甲地出发,沿平直公路开往乙地,汽车先做匀加速直线运动,接着做匀减速直线运动,开到乙地刚好停止,其图像如图所示,那么在和两段时间内 ( )
A. 加速度大小之比为 B. 位移大小之比为
C. 平均速度大小之比为 D. 平均速度大小之比为
9. 下列图像能反映物体做直线运动经没有回到初始位置的是( )
A. B.
C. D.
二、多选题
10. 某校体育课上正在进行短跑测试,一同学从起点由静止开始以的加速度做匀加速运动,后,改做匀速运动直至到达终点,接着以的加速度做匀减速运动,经进入迎接区,如图所示,则下列说法正确的是 ( )
A. 该同学的成绩为 B. 该同学的成绩为
C. 终点线到迎接区边界的距离为 D. 终点线到迎接区边界的距离为
11. 甲、乙两辆汽车在同一水平直道上运动,其运动的位移时间图像图像如图所示,则下列关于两车运动情况的说法中正确的是 ( )
A. 甲车先做减速直线运动,后做匀速直线运动
B. 乙车在内的平均速度大小为
C. 在内,甲、乙两车相遇两次
D. 若乙车做匀变速直线运动,则图线上点所对应的瞬时速度大小一定大于
12. 如图所示,汽车以的速度匀速驶向路口,当行驶至距路口停车线处时,绿灯还有熄灭.而该汽车在绿灯熄灭时刚好停在停车线处,则汽车运动的图像可能是 ( )
A. B. C. D.
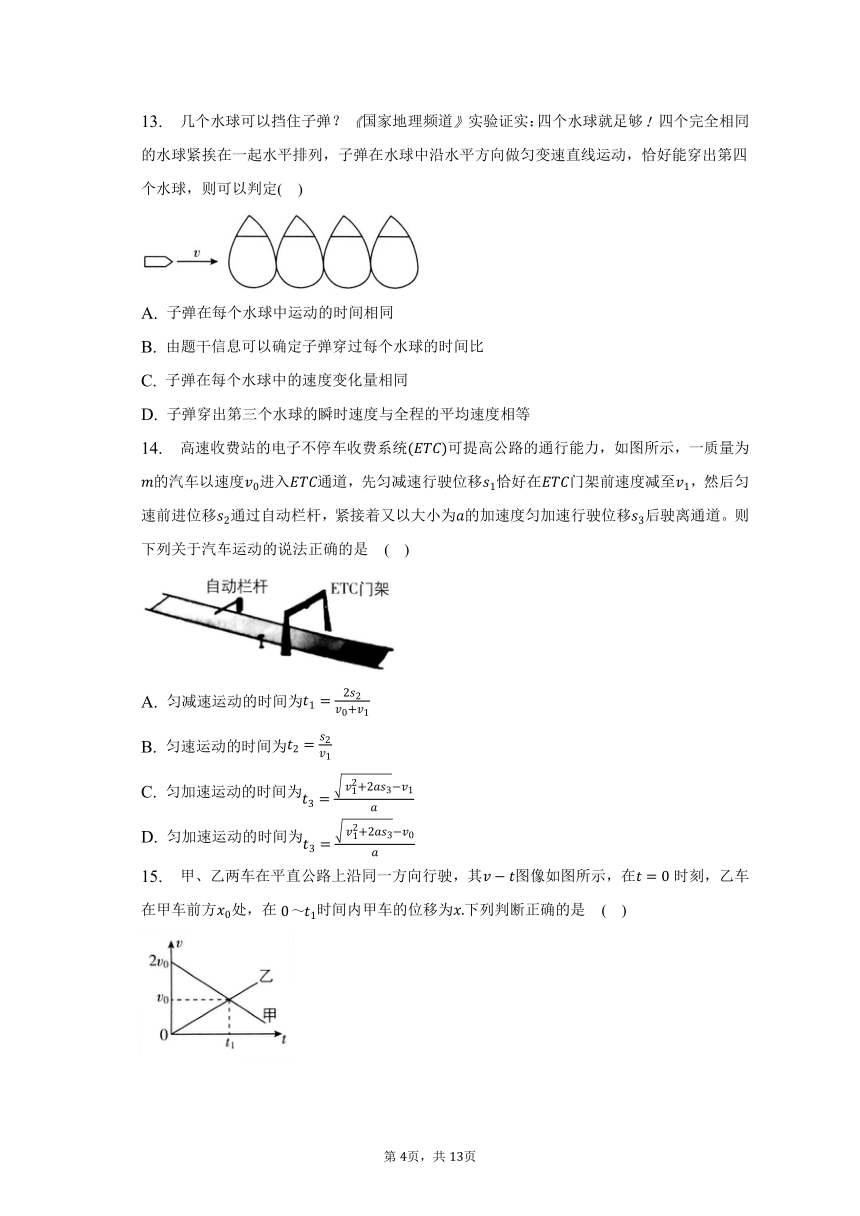
13. 几个水球可以挡住子弹?国家地理频道实验证实:四个水球就足够四个完全相同的水球紧挨在一起水平排列,子弹在水球中沿水平方向做匀变速直线运动,恰好能穿出第四个水球,则可以判定( )
A. 子弹在每个水球中运动的时间相同
B. 由题干信息可以确定子弹穿过每个水球的时间比
C. 子弹在每个水球中的速度变化量相同
D. 子弹穿出第三个水球的瞬时速度与全程的平均速度相等
14. 高速收费站的电子不停车收费系统可提高公路的通行能力,如图所示,一质量为的汽车以速度进入通道,先匀减速行驶位移恰好在门架前速度减至,然后匀速前进位移通过自动栏杆,紧接着又以大小为的加速度匀加速行驶位移后驶离通道。则下列关于汽车运动的说法正确的是 ( )
A. 匀减速运动的时间为
B. 匀速运动的时间为
C. 匀加速运动的时间为
D. 匀加速运动的时间为
15. 甲、乙两车在平直公路上沿同一方向行驶,其图像如图所示,在时刻,乙车在甲车前方处,在时间内甲车的位移为下列判断正确的是 ( )
A. 若甲、乙在时刻相遇,则
B. 若甲、乙在时刻相遇,则下次相遇的时刻为
C. 若,则甲、乙一定相遇两次
D. 若,则甲、乙一定相遇两次
三、实验题
16. 图中装置可用来探究物块的运动情况,细线平行于桌面,遮光片的宽度为,两光电门之间的距离为,将物块从光电门的左侧由静止释放,分别测出遮光片通过光电门、所用的时间为和,用遮光片通过光电门的平均速度表示遮光片竖直中线通过光电门的瞬时速度。
利用实验中测出的物理量符号,表示出物块运动的加速度________;
遮光片通过光电门的平均速度________填“大于”“等于”或“小于”遮光片竖直中线通过光电门的瞬时速度,由此会产生误差,请写出一种减小这一误差的方法:________________。
四、计算题
17. 物体从静止开始做匀加速直线运动,加速度为,求:
物体在内的位移;
物体在第内的位移;
物体在第二个内的位移.
18. 年月日,中华人民共和国成立周年阅兵在北京隆重举行,共有辆东风猛士首次在阅兵活动中亮相.型吨高机动越野车的机动性、适应性、安全性、耐用性十分优秀,是我国自主研发的多用途,高技术军用越野车.该车型既能高速行驶于铺装路面,又能快速行驶于急造军路、乡村土路.若该型车从静止开始,在水平路面上做匀加速直线运动,加速到大约需要时间求:
该车此过程的加速度大小.
在加速的这内该车位移的大小.
19. 在某市区内,一辆小汽车在平直公路上以速度向东匀速行驶,一位观光游客正由南向北从斑马线上横过马路,汽车司机发现前方有危险游客正在处向北走经作出反应,从点开始紧急刹车,但仍将步行至处的游客撞伤,该汽车最终在处停下.为了清晰了解事故现场,现以如图示之.为了判断汽车司机是否超速行驶,并测出肇事汽车速度,警方派一车胎磨损情况与肇事车相当的警车以法定最高速度行驶在同一马路的同一地段,在肇事汽车的出事点急刹车,恰好也在点停下来.在事故现场测得,、.
该肇事汽车的初速度是多大?
游客横过马路的速度是多大?
20. 交通规定:黄灯亮时车头已经越过停车线的车辆可以继续前行,车头未越过停车线的车辆若继续前行则视为闯黄灯。现有甲、乙两汽车正沿同一平直马路同向匀速行驶,甲车在前,乙车在后,当两车快要到十字路口时,甲车司机看到黄灯开始闪烁,黄灯提示后将转为红灯,请问:
若甲车在黄灯开始闪烁时开始刹车,要使车在黄灯闪烁的时间内停下来且刹车距离不得大于,则甲车刹车前的行驶速度不能超过多少?
若甲、乙两车均以的速度驶向路口,乙车司机看到甲车开始刹车后也开始刹车乙车司机的反应时间,已知甲车、乙车刹车时产生的加速度大小分别为、,若甲车司机看到黄灯闪烁时车头距停车线,要避免闯红灯,他的最长反应时间为多少?
满足第问的条件下,为保证两车在紧急刹车过程中不相撞,甲、乙两车刹车前的最小距离为多大?两车的车身长度不计,可以看成质点
答案和解析
1.【答案】
【解析】根据和知,只有在物体的初速度为零的情况下,物体的速度才与时间成正比,位移才与时间的平方成正比,故A、B错误;由可知,一定,则物体的速度在一定时间内发生的变化与这段时间成正比,故C正确;当物体做匀减速运动时,速度随着时间减小但位移可以随着时间增大,故D错误.
2.【答案】
【解析】在图像中,图像与坐标轴围成的面积表示位移.在时间轴上方的面积表示位移为正,下方的面积表示位移为负.由题图可知:时刻前物体位移为正,时刻后物体位移为负,时刻物体位移最大.故选B.
3.【答案】
【解析】设物体到达斜面底端的速度为,则两段运动过程的平均速度均为,
由得,故选C。
4.【答案】
【解析】加速度越大,车越容易停下来,当汽车恰好到达斑马线前停下时,加速度最小,根据速度位移公式,得,“”表示加速度方向与初速度方向相反,选项C正确。
5.【答案】
【解析】第一阶段,设汽车做匀加速直线运动时的加速度大小为,则由运动学公式得,对应图线是开口向右的抛物线;第二阶段,设刹车时汽车的位移为,速度为,其后做减速运动的加速度大小为,则减速过程有,即,对应图线是开口向左的抛物线.综上所述,只有选项A正确.
6.【答案】
【解析】
【分析】
根据匀变速直线运动的位移时间公式得出汽车的初速度和加速度,结合速度时间公式求出汽车速度减为零的时间,判断汽车是否停止,再结合位移公式求出刹车的位移。
本题考查了运动学中的刹车问题,是道易错题,注意汽车速度减为零后不再运动,结合运动学公式和推论进行求解。
【解答】
对比公式可得,,
汽车静止所需时间为,
所以前内的位移等于前内的位移,
故,C正确。
7.【答案】
【解析】质点做匀加速直线运动,由可得,,解得,选项正确;
第一个内的平均速度,此速度等于该阶段中间时刻的瞬时速度,故第末的速度大小为,选项错误;
由匀变速直线运动公式,代入第末的速度与加速度,可得第末的速度大小为,选项错误;
由匀变速直线运动的推论可知质点在内的平均速度等于末的瞬时速度为,选项错误。
8.【答案】
【解析】根据图线的斜率等于加速度可知,在和两段时间内汽车加速度大小之比为,故A错误;
根据图线与轴所围图形的面积等于位移大小可知,和两段时间内位移大小之比为,故B错误;
和两段时间内平均速度大小之比,故C错误,D正确。
9.【答案】
【解析】位移时间图像表示物体在不同时刻的位置坐标,项中图像表示物体沿轴正方向运动后又返回初始位置,故A不符合题意;速度时间图像表示物体的速度随时间的变化情况,由项中图像可知物体的速度一直为正,物体没有回到初始位置,故B符合题意;由项中图像可知物体在第内沿正方向运动,在第内沿负方向运动,经回到初始位置,故C不符合题意;由项中图像可知,物体在第内沿正方向运动,在第内沿负方向运动,经回到初始位置,故D不符合题意.
10.【答案】
【解析】
【分析】
根据匀变速直线运动的位移时间公式求出匀加速运动的位移,从而得出匀速运动的位移,根据速度时间公式求出匀加速运动的末速度,结合匀速运动的公式求出匀速运动的时间.
根据匀变速直线运动的位移时间公式求出匀减速运动的位移,从而得出终点线到迎接区边界的距离.
解决本题的关键掌握匀变速直线运动的运动学公式,并能灵活运用,基础题。
【解答】
该同学由静止开始运动后的速度为,
此时的位移为,
则剩余位移所用时间,
总时间为,故A正确,B错误;
从终点线到迎接区该同学做匀减速运动,则有
,故C正确,D错误.
11.【答案】
【解析】图像的斜率表示速度,根据题图可知,甲车先做匀速直线运动,后静止,故A错误;乙车在内的位移,则该时间内乙车的平均速度大小为,故B正确;图像中的交点表示相遇,根据题图可知,内,两车相遇两次,故C正确;若乙车做匀变速直线运动,则乙车做匀加速直线运动,中间时刻的速度等于该时间内的平均速度,所以末的瞬时速度大小等于,则点对应的瞬时速度大小一定大于,故D正确.
12.【答案】
【解析】
【分析】
由题,该汽车在绿灯熄灭时刚好停在停车线处,在通过的位移正好是,根据“面积”确定位移是的速度图象才符合题意。
本题是实际问题,首先要读懂题意,其次抓住速度图象的“面积”等于位移进行选择。
【解答】
图像与坐标轴所围“面积”表示位移,、选项中图像的“面积”不等于,选项中图像的“面积”可能等于,选项中图像的“面积”正好等于,故B、符合题意.
13.【答案】
【解析】设水球的直径为,子弹运动的过程为匀减速直线运动,直到末速度为零,应用逆向思维,相当于子弹做初速度为零的匀加速直线运动;
因为通过最后个、最后个、最后个、全部个的位移分别为,,和,根据知,时间之比为,所以子弹在每个水球中运动的时间不同,
由以上的分析可知,子弹依次穿过个水球的时间之比为,故A错误,B正确;
子弹在水球中沿水平方向做匀变速直线运动,由可知,运动的时间不同,则速度的变化量不同,故C错误;
由的分析可知,子弹穿过前个水球的时间与穿过第个水球的时间相等,由匀变速直线运动的特点可知,子弹穿出第三个水球的瞬时速度与全程的平均速度相等,故D正确。
14.【答案】
【解析】由,得汽车做匀减速运动的时间为,A错误;
由,得汽车做匀速运动的时间为,B正确;
由,得汽车做匀加速运动的时间为,C正确,D错误。
15.【答案】
【解析】由题图可知,甲车的初速度等于,在时间内,甲车的位移为,则乙车的位移为若甲、乙在时刻相遇,则,故A错误;
若甲、乙在时刻相遇,
由图像可知,,由图像中的对称关系可知,下次相遇的时刻为,故B、D正确;
若,两车不能相遇,故C错误。
16.【答案】 小于,减小遮光片的宽度。
【解析】解:遮光片通过光电门的时间极短时,可以用平均速度近似表示中间时刻的瞬时速度,故遮光片通过点的速度为,通过点的速度为,
物块做匀加速直线运动,由速度位移公式得,
加速度为;
遮光片通过光电门的平均速度等于这一过程中间时刻的瞬时速度,而遮光片做加速运动前一半的时间内的位移小于后一半时间内的位移,所以在中间时刻,遮光片的竖直中线尚未到达光电门,所以遮光片通过光电门的平均速度小于遮光片竖直中线通过光电门的瞬时速度,
为减小实验的误差,可以减小遮光片的宽度。
17.【答案】解:由匀变速直线运动位移公式可得
.
物体在第末的速度第初的速度 故物体在第内的位移 .
物体在第末的速度,也是物体在第二个的初速度,故物体在第二个内的位移
【解析】见答案
18.【答案】解:,则汽车的加速度大小为;
这内该车的位移大小为。
【解析】本题主要考查加速度的定义式以及匀变速直线运动规律的应用。
结合题意,由加速度的定义式求解汽车的加速度大小;
结合匀变速直线运动的平均速度,由运动学公式求解位移的大小。
19.【答案】解:以警车为研究对象,则,将、代入,得警车刹车时加速度大小为,因为警车行驶条件与肇事汽车相同,则肇事汽车刹车时的加速度大小也为,所以肇事汽车的初速度.
肇事汽车在出事点的速度,肇事汽车通过段的平均速度
,肇事汽车通过段的时间所以游客横过马路的速度大小.
【解析】根据速度位移公式求出警车刹车的加速度,抓住加速度相同,结合速度位移公式求出肇事车的初速度.
根据匀变速直线运动的位移时间公式求出肇事车的运动时间,结合反应时间求出游客运行时间,从而根据平均速度的定义式求出游客横过马路的平均速度大小.
在解决物理问题时,有时语言描述不好懂,我们可以结合运动示意图更清晰直观的理解题目,通过物体的运动规律,结合运动学公式灵活求解.
20.【答案】解:设在满足条件的情况下,甲车的最大行驶速度为,则,,
解得,故甲车刹车前的行驶速度不能超过;
对甲车有,代入数据解得,故最长反应时间为;
设乙车减速运动的时间为时甲、乙两车速度相等,若此前两车不相撞,则此后两车也不会相撞,
两车速度相等时,有,
解得,
则有,
,,
,
故甲、乙两车刹车前的最小距离为。
【解析】见答案
第1页,共1页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1. 一物体做匀变速直线运动,下列说法中正确的是( )
A. 物体的末速度一定与时间成正比
B. 物体的位移一定与时间的平方成正比
C. 物体的速度在一定时间内发生的变化与这段时间成正比
D. 若为匀加速运动,速度和位移都随时间增加;若为匀减速运动,速度和位移都随时间减小
2. 如图所示是物体运动的图像,从开始,物体位移最大的时刻是 ( )
A. B. C. D.
3. 一物体从斜面上某点由静止开始做匀加速直线运动,经过到达斜面底端,并开始在水平地面上做匀减速直线运动,经过停止。设物体由斜面底端运动到水平地面上时速度大小不变,则物体在斜面上的位移大小与在水平地面上的位移大小之比是( )
A. B. C. D.
4. “道路千万条,安全第一条”,一辆汽车在平直公路上以的速度匀速行驶,驾驶员发现前方处的斑马线上有行人,驾驶员立即刹车使汽车做匀减速直线运动并最终停在斑马线之前,则刹车后汽车的加速度大小至少为( )
A. B. C. D.
5. 一汽车从静止开始做匀加速直线运动,然后刹车做匀减速直线运动,直到停止.下列速度和位移的关系图像中,能描述该过程的是 ( )
A. B. C. D.
6. 汽车在水平路面上刹车,其位移与时间的关系是,则它在前内的位移是 ( )
A. B. C. D.
7. 一质点在连续的内做匀加速直线运动,在第一个内位移为,第二个内位移为,下面说法正确的是( )
A. 质点在第末的速度大小为 B. 质点在第末的速度大小为
C. 质点的加速度大小为 D. 质点在内的平均速度大小为
8. 一辆汽车从静止开始由甲地出发,沿平直公路开往乙地,汽车先做匀加速直线运动,接着做匀减速直线运动,开到乙地刚好停止,其图像如图所示,那么在和两段时间内 ( )
A. 加速度大小之比为 B. 位移大小之比为
C. 平均速度大小之比为 D. 平均速度大小之比为
9. 下列图像能反映物体做直线运动经没有回到初始位置的是( )
A. B.
C. D.
二、多选题
10. 某校体育课上正在进行短跑测试,一同学从起点由静止开始以的加速度做匀加速运动,后,改做匀速运动直至到达终点,接着以的加速度做匀减速运动,经进入迎接区,如图所示,则下列说法正确的是 ( )
A. 该同学的成绩为 B. 该同学的成绩为
C. 终点线到迎接区边界的距离为 D. 终点线到迎接区边界的距离为
11. 甲、乙两辆汽车在同一水平直道上运动,其运动的位移时间图像图像如图所示,则下列关于两车运动情况的说法中正确的是 ( )
A. 甲车先做减速直线运动,后做匀速直线运动
B. 乙车在内的平均速度大小为
C. 在内,甲、乙两车相遇两次
D. 若乙车做匀变速直线运动,则图线上点所对应的瞬时速度大小一定大于
12. 如图所示,汽车以的速度匀速驶向路口,当行驶至距路口停车线处时,绿灯还有熄灭.而该汽车在绿灯熄灭时刚好停在停车线处,则汽车运动的图像可能是 ( )
A. B. C. D.
13. 几个水球可以挡住子弹?国家地理频道实验证实:四个水球就足够四个完全相同的水球紧挨在一起水平排列,子弹在水球中沿水平方向做匀变速直线运动,恰好能穿出第四个水球,则可以判定( )
A. 子弹在每个水球中运动的时间相同
B. 由题干信息可以确定子弹穿过每个水球的时间比
C. 子弹在每个水球中的速度变化量相同
D. 子弹穿出第三个水球的瞬时速度与全程的平均速度相等
14. 高速收费站的电子不停车收费系统可提高公路的通行能力,如图所示,一质量为的汽车以速度进入通道,先匀减速行驶位移恰好在门架前速度减至,然后匀速前进位移通过自动栏杆,紧接着又以大小为的加速度匀加速行驶位移后驶离通道。则下列关于汽车运动的说法正确的是 ( )
A. 匀减速运动的时间为
B. 匀速运动的时间为
C. 匀加速运动的时间为
D. 匀加速运动的时间为
15. 甲、乙两车在平直公路上沿同一方向行驶,其图像如图所示,在时刻,乙车在甲车前方处,在时间内甲车的位移为下列判断正确的是 ( )
A. 若甲、乙在时刻相遇,则
B. 若甲、乙在时刻相遇,则下次相遇的时刻为
C. 若,则甲、乙一定相遇两次
D. 若,则甲、乙一定相遇两次
三、实验题
16. 图中装置可用来探究物块的运动情况,细线平行于桌面,遮光片的宽度为,两光电门之间的距离为,将物块从光电门的左侧由静止释放,分别测出遮光片通过光电门、所用的时间为和,用遮光片通过光电门的平均速度表示遮光片竖直中线通过光电门的瞬时速度。
利用实验中测出的物理量符号,表示出物块运动的加速度________;
遮光片通过光电门的平均速度________填“大于”“等于”或“小于”遮光片竖直中线通过光电门的瞬时速度,由此会产生误差,请写出一种减小这一误差的方法:________________。
四、计算题
17. 物体从静止开始做匀加速直线运动,加速度为,求:
物体在内的位移;
物体在第内的位移;
物体在第二个内的位移.
18. 年月日,中华人民共和国成立周年阅兵在北京隆重举行,共有辆东风猛士首次在阅兵活动中亮相.型吨高机动越野车的机动性、适应性、安全性、耐用性十分优秀,是我国自主研发的多用途,高技术军用越野车.该车型既能高速行驶于铺装路面,又能快速行驶于急造军路、乡村土路.若该型车从静止开始,在水平路面上做匀加速直线运动,加速到大约需要时间求:
该车此过程的加速度大小.
在加速的这内该车位移的大小.
19. 在某市区内,一辆小汽车在平直公路上以速度向东匀速行驶,一位观光游客正由南向北从斑马线上横过马路,汽车司机发现前方有危险游客正在处向北走经作出反应,从点开始紧急刹车,但仍将步行至处的游客撞伤,该汽车最终在处停下.为了清晰了解事故现场,现以如图示之.为了判断汽车司机是否超速行驶,并测出肇事汽车速度,警方派一车胎磨损情况与肇事车相当的警车以法定最高速度行驶在同一马路的同一地段,在肇事汽车的出事点急刹车,恰好也在点停下来.在事故现场测得,、.
该肇事汽车的初速度是多大?
游客横过马路的速度是多大?
20. 交通规定:黄灯亮时车头已经越过停车线的车辆可以继续前行,车头未越过停车线的车辆若继续前行则视为闯黄灯。现有甲、乙两汽车正沿同一平直马路同向匀速行驶,甲车在前,乙车在后,当两车快要到十字路口时,甲车司机看到黄灯开始闪烁,黄灯提示后将转为红灯,请问:
若甲车在黄灯开始闪烁时开始刹车,要使车在黄灯闪烁的时间内停下来且刹车距离不得大于,则甲车刹车前的行驶速度不能超过多少?
若甲、乙两车均以的速度驶向路口,乙车司机看到甲车开始刹车后也开始刹车乙车司机的反应时间,已知甲车、乙车刹车时产生的加速度大小分别为、,若甲车司机看到黄灯闪烁时车头距停车线,要避免闯红灯,他的最长反应时间为多少?
满足第问的条件下,为保证两车在紧急刹车过程中不相撞,甲、乙两车刹车前的最小距离为多大?两车的车身长度不计,可以看成质点
答案和解析
1.【答案】
【解析】根据和知,只有在物体的初速度为零的情况下,物体的速度才与时间成正比,位移才与时间的平方成正比,故A、B错误;由可知,一定,则物体的速度在一定时间内发生的变化与这段时间成正比,故C正确;当物体做匀减速运动时,速度随着时间减小但位移可以随着时间增大,故D错误.
2.【答案】
【解析】在图像中,图像与坐标轴围成的面积表示位移.在时间轴上方的面积表示位移为正,下方的面积表示位移为负.由题图可知:时刻前物体位移为正,时刻后物体位移为负,时刻物体位移最大.故选B.
3.【答案】
【解析】设物体到达斜面底端的速度为,则两段运动过程的平均速度均为,
由得,故选C。
4.【答案】
【解析】加速度越大,车越容易停下来,当汽车恰好到达斑马线前停下时,加速度最小,根据速度位移公式,得,“”表示加速度方向与初速度方向相反,选项C正确。
5.【答案】
【解析】第一阶段,设汽车做匀加速直线运动时的加速度大小为,则由运动学公式得,对应图线是开口向右的抛物线;第二阶段,设刹车时汽车的位移为,速度为,其后做减速运动的加速度大小为,则减速过程有,即,对应图线是开口向左的抛物线.综上所述,只有选项A正确.
6.【答案】
【解析】
【分析】
根据匀变速直线运动的位移时间公式得出汽车的初速度和加速度,结合速度时间公式求出汽车速度减为零的时间,判断汽车是否停止,再结合位移公式求出刹车的位移。
本题考查了运动学中的刹车问题,是道易错题,注意汽车速度减为零后不再运动,结合运动学公式和推论进行求解。
【解答】
对比公式可得,,
汽车静止所需时间为,
所以前内的位移等于前内的位移,
故,C正确。
7.【答案】
【解析】质点做匀加速直线运动,由可得,,解得,选项正确;
第一个内的平均速度,此速度等于该阶段中间时刻的瞬时速度,故第末的速度大小为,选项错误;
由匀变速直线运动公式,代入第末的速度与加速度,可得第末的速度大小为,选项错误;
由匀变速直线运动的推论可知质点在内的平均速度等于末的瞬时速度为,选项错误。
8.【答案】
【解析】根据图线的斜率等于加速度可知,在和两段时间内汽车加速度大小之比为,故A错误;
根据图线与轴所围图形的面积等于位移大小可知,和两段时间内位移大小之比为,故B错误;
和两段时间内平均速度大小之比,故C错误,D正确。
9.【答案】
【解析】位移时间图像表示物体在不同时刻的位置坐标,项中图像表示物体沿轴正方向运动后又返回初始位置,故A不符合题意;速度时间图像表示物体的速度随时间的变化情况,由项中图像可知物体的速度一直为正,物体没有回到初始位置,故B符合题意;由项中图像可知物体在第内沿正方向运动,在第内沿负方向运动,经回到初始位置,故C不符合题意;由项中图像可知,物体在第内沿正方向运动,在第内沿负方向运动,经回到初始位置,故D不符合题意.
10.【答案】
【解析】
【分析】
根据匀变速直线运动的位移时间公式求出匀加速运动的位移,从而得出匀速运动的位移,根据速度时间公式求出匀加速运动的末速度,结合匀速运动的公式求出匀速运动的时间.
根据匀变速直线运动的位移时间公式求出匀减速运动的位移,从而得出终点线到迎接区边界的距离.
解决本题的关键掌握匀变速直线运动的运动学公式,并能灵活运用,基础题。
【解答】
该同学由静止开始运动后的速度为,
此时的位移为,
则剩余位移所用时间,
总时间为,故A正确,B错误;
从终点线到迎接区该同学做匀减速运动,则有
,故C正确,D错误.
11.【答案】
【解析】图像的斜率表示速度,根据题图可知,甲车先做匀速直线运动,后静止,故A错误;乙车在内的位移,则该时间内乙车的平均速度大小为,故B正确;图像中的交点表示相遇,根据题图可知,内,两车相遇两次,故C正确;若乙车做匀变速直线运动,则乙车做匀加速直线运动,中间时刻的速度等于该时间内的平均速度,所以末的瞬时速度大小等于,则点对应的瞬时速度大小一定大于,故D正确.
12.【答案】
【解析】
【分析】
由题,该汽车在绿灯熄灭时刚好停在停车线处,在通过的位移正好是,根据“面积”确定位移是的速度图象才符合题意。
本题是实际问题,首先要读懂题意,其次抓住速度图象的“面积”等于位移进行选择。
【解答】
图像与坐标轴所围“面积”表示位移,、选项中图像的“面积”不等于,选项中图像的“面积”可能等于,选项中图像的“面积”正好等于,故B、符合题意.
13.【答案】
【解析】设水球的直径为,子弹运动的过程为匀减速直线运动,直到末速度为零,应用逆向思维,相当于子弹做初速度为零的匀加速直线运动;
因为通过最后个、最后个、最后个、全部个的位移分别为,,和,根据知,时间之比为,所以子弹在每个水球中运动的时间不同,
由以上的分析可知,子弹依次穿过个水球的时间之比为,故A错误,B正确;
子弹在水球中沿水平方向做匀变速直线运动,由可知,运动的时间不同,则速度的变化量不同,故C错误;
由的分析可知,子弹穿过前个水球的时间与穿过第个水球的时间相等,由匀变速直线运动的特点可知,子弹穿出第三个水球的瞬时速度与全程的平均速度相等,故D正确。
14.【答案】
【解析】由,得汽车做匀减速运动的时间为,A错误;
由,得汽车做匀速运动的时间为,B正确;
由,得汽车做匀加速运动的时间为,C正确,D错误。
15.【答案】
【解析】由题图可知,甲车的初速度等于,在时间内,甲车的位移为,则乙车的位移为若甲、乙在时刻相遇,则,故A错误;
若甲、乙在时刻相遇,
由图像可知,,由图像中的对称关系可知,下次相遇的时刻为,故B、D正确;
若,两车不能相遇,故C错误。
16.【答案】 小于,减小遮光片的宽度。
【解析】解:遮光片通过光电门的时间极短时,可以用平均速度近似表示中间时刻的瞬时速度,故遮光片通过点的速度为,通过点的速度为,
物块做匀加速直线运动,由速度位移公式得,
加速度为;
遮光片通过光电门的平均速度等于这一过程中间时刻的瞬时速度,而遮光片做加速运动前一半的时间内的位移小于后一半时间内的位移,所以在中间时刻,遮光片的竖直中线尚未到达光电门,所以遮光片通过光电门的平均速度小于遮光片竖直中线通过光电门的瞬时速度,
为减小实验的误差,可以减小遮光片的宽度。
17.【答案】解:由匀变速直线运动位移公式可得
.
物体在第末的速度第初的速度 故物体在第内的位移 .
物体在第末的速度,也是物体在第二个的初速度,故物体在第二个内的位移
【解析】见答案
18.【答案】解:,则汽车的加速度大小为;
这内该车的位移大小为。
【解析】本题主要考查加速度的定义式以及匀变速直线运动规律的应用。
结合题意,由加速度的定义式求解汽车的加速度大小;
结合匀变速直线运动的平均速度,由运动学公式求解位移的大小。
19.【答案】解:以警车为研究对象,则,将、代入,得警车刹车时加速度大小为,因为警车行驶条件与肇事汽车相同,则肇事汽车刹车时的加速度大小也为,所以肇事汽车的初速度.
肇事汽车在出事点的速度,肇事汽车通过段的平均速度
,肇事汽车通过段的时间所以游客横过马路的速度大小.
【解析】根据速度位移公式求出警车刹车的加速度,抓住加速度相同,结合速度位移公式求出肇事车的初速度.
根据匀变速直线运动的位移时间公式求出肇事车的运动时间,结合反应时间求出游客运行时间,从而根据平均速度的定义式求出游客横过马路的平均速度大小.
在解决物理问题时,有时语言描述不好懂,我们可以结合运动示意图更清晰直观的理解题目,通过物体的运动规律,结合运动学公式灵活求解.
20.【答案】解:设在满足条件的情况下,甲车的最大行驶速度为,则,,
解得,故甲车刹车前的行驶速度不能超过;
对甲车有,代入数据解得,故最长反应时间为;
设乙车减速运动的时间为时甲、乙两车速度相等,若此前两车不相撞,则此后两车也不会相撞,
两车速度相等时,有,
解得,
则有,
,,
,
故甲、乙两车刹车前的最小距离为。
【解析】见答案
第1页,共1页
