2024年中考数学复习专项练习:一次函数(含答案)
文档属性
| 名称 | 2024年中考数学复习专项练习:一次函数(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 252.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-14 00:00:00 | ||
图片预览


文档简介
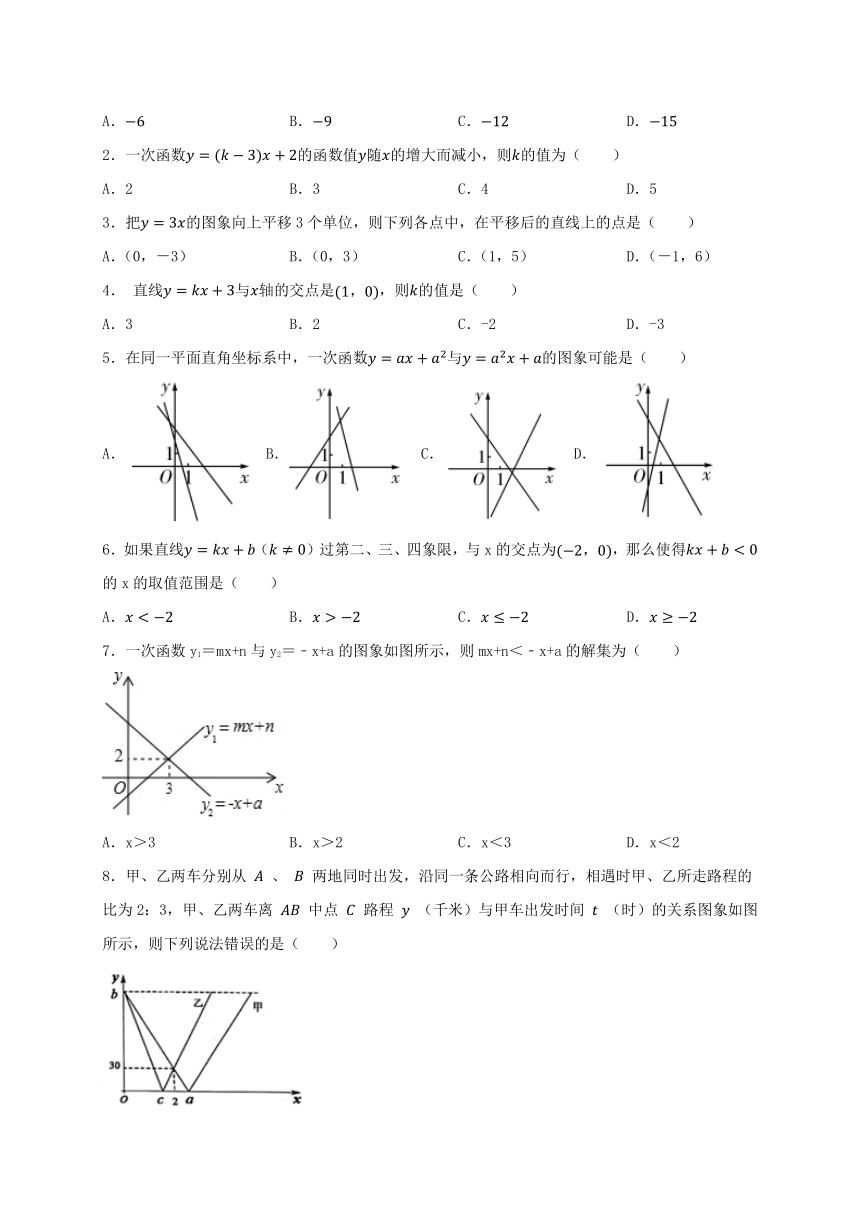
2024年中考数学复习 专项提升练习:一次函数
知识点回顾
1.正比例函数的图象及性质:正比例函数y=kx(k是常数,k≠0)的图象是一条经过原点的直线,称为直线y=kx。
y=kx 图像 经过象限 增减性
k>0 三、一 y随着x的增大而增大
k<0 二、四 y随着x的增大而减小
2.一次函数的图象及性质:一次函数y=kx+b(k、b是常数,k≠0)的图象是一条直线,称为直线y=kx+b。当k>0时,直线y=kx+b从左向右上升,即y随着x的增大而增大;当k<0时,直线y=kx+b从左向右下降,即y随着x的增大而减小。
y=kx+b 图像 经过象限 增减性
k>0,b>0 三、二、一 y随着x的增大而增大
k>0,b<0 三、四、一
k<0,b>0 二、一、四 y随着x的增大而减小
k<0,b<0 二、三、四
提升练习
一、选择题
1.变量y与x之间的关系是,当自变量时,因变量y的值是( )
A. B. C. D.
2.一次函数的函数值随的增大而减小,则的值为( )
A.2 B.3 C.4 D.5
3.把的图象向上平移3个单位,则下列各点中,在平移后的直线上的点是( )
A.(0,-3) B.(0,3) C.(1,5) D.(-1,6)
4. 直线与轴的交点是,则的值是( )
A.3 B.2 C.-2 D.-3
5.在同一平面直角坐标系中,一次函数与的图象可能是( )
A. B. C. D.
6.如果直线()过第二、三、四象限,与x的交点为,那么使得的x的取值范围是( )
A. B. C. D.
7.一次函数y1=mx+n与y2=﹣x+a的图象如图所示,则mx+n<﹣x+a的解集为( )
A.x>3 B.x>2 C.x<3 D.x<2
8.甲、乙两车分别从 、 两地同时出发,沿同一条公路相向而行,相遇时甲、乙所走路程的比为2:3,甲、乙两车离 中点 路程 (千米)与甲车出发时间 (时)的关系图象如图所示,则下列说法错误的是( )
A.乙车的速度为90千米/时
B. 的值为
C. 的值为150
D.当甲、乙车相距30千米时,甲行走了 或
二、填空题
9.已知一次函数y=(m+2)x-5,若y随x的增大而减小,则m的取值范围为 .
10.如图,一次函数与x轴、y轴分别交于A、B两点,则不等式的解集是 .
11.已知一次函数的图象经过点和,则 .
12.一次函数y=2x+4的图象与x轴、y轴的交点分别为A,B,则线段AB的长为 .
13.小明家到学校的路程是米,小明从家出发,以平均每分钟米的速度步行去上学,则他离学校的路程(米)与行走的时间(分)之间的关系式是 .
三、解答题
14.已知与成正比例,且时,.
(1)求与的函数关系式;
(2)将所得函数图象平移,使它过点.求平移后直线的解析式.
15.一条公路上依次有A,C,B三地,甲、乙两车分别从A,B两地同时出发,匀速行驶,甲车驶向C地,乙车从B地驶向C地,停1h后按原速原路返回到B地.两车与C地的距离y(单位:)与甲车出发的时间x(单位:h)之间的函数图象如图所示.
(1)求甲、乙两车的速度;
(2)求乙车从出发到返回B地的过程中y与x之间的函数解析式;
(3)直接写出甲车出发多长时间时,甲、乙两车相距.
16.如图,已知直线经过点,,与直线交于C点、
(1)求直线的解析式以及以与x轴的交点D的坐标;
(2)求C点的坐标;
(3)根据图象,直接写出关于的不等式时x的取值范围.
17.荆州古城旁“荆街”某商铺打算购进A,B两种文创饰品对游客销售.已知1400元采购A种的件数是630元采购B种件数的2倍,A种的进价比B种的进价每件多1元,两种饰品的售价均为每件15元;计划采购这两种饰品共600件,采购B种的件数不低于390件,不超过A种件数的4倍.
(1)求A,B饰品每件的进价分别为多少元?
(2)若采购这两种饰品只有一种情况可优惠,即一次性采购A种超过150件时,A种超过的部分按进价打6折.设购进A种饰品x件,①求x的取值范围;②设计能让这次采购的饰品获利最大的方案,并求出最大利润.
参考答案
1.B
2.A
3.B
4.D
5.D
6.B
7.C
8.D
9.m<-2
10.
11.-6
12.
13.
14.(1)
(2)
15.(1)甲车的速度为,乙车的速度为
(2)
(3)甲车出发或或时,甲、乙两车相距300km
16.(1)解:∵直线y1=kx+b经过点A(5,0),B(1,4)
∴,解得
∴直线AB的解析式为:y1=-x+5;
在y2=2x-4中,令y=0,则x=2
∴y2与x轴的交点D的坐标为(2,0);
(2)接:解得
∴点C坐标为(3,2);
(3)解:由图象可知,不等式时x的取值范围为.
17.(1)解:设A种饰品每件的进价为元,则B种饰品每件的进价为
由题意得: 解得:
经检验,是所列方程的根,且符合题意.
A种饰品每件进价为10元,B种饰品每件进价为9元
(2)解:①根据题意得: 解得:
购进A种饰品件数的取值范围为:
②设采购A种饰品件时的总利润为元.
当时, 即
,随的增大而减小. 当时,有最大值3480.
当时,
整理得: 3>0,随的增大而增大.
当时,有最大值3630.
,w的最大值为3630,此时.
即当采购A种饰品210件,B种饰品390件时,商铺获利最大,最大利润为3630元.
知识点回顾
1.正比例函数的图象及性质:正比例函数y=kx(k是常数,k≠0)的图象是一条经过原点的直线,称为直线y=kx。
y=kx 图像 经过象限 增减性
k>0 三、一 y随着x的增大而增大
k<0 二、四 y随着x的增大而减小
2.一次函数的图象及性质:一次函数y=kx+b(k、b是常数,k≠0)的图象是一条直线,称为直线y=kx+b。当k>0时,直线y=kx+b从左向右上升,即y随着x的增大而增大;当k<0时,直线y=kx+b从左向右下降,即y随着x的增大而减小。
y=kx+b 图像 经过象限 增减性
k>0,b>0 三、二、一 y随着x的增大而增大
k>0,b<0 三、四、一
k<0,b>0 二、一、四 y随着x的增大而减小
k<0,b<0 二、三、四
提升练习
一、选择题
1.变量y与x之间的关系是,当自变量时,因变量y的值是( )
A. B. C. D.
2.一次函数的函数值随的增大而减小,则的值为( )
A.2 B.3 C.4 D.5
3.把的图象向上平移3个单位,则下列各点中,在平移后的直线上的点是( )
A.(0,-3) B.(0,3) C.(1,5) D.(-1,6)
4. 直线与轴的交点是,则的值是( )
A.3 B.2 C.-2 D.-3
5.在同一平面直角坐标系中,一次函数与的图象可能是( )
A. B. C. D.
6.如果直线()过第二、三、四象限,与x的交点为,那么使得的x的取值范围是( )
A. B. C. D.
7.一次函数y1=mx+n与y2=﹣x+a的图象如图所示,则mx+n<﹣x+a的解集为( )
A.x>3 B.x>2 C.x<3 D.x<2
8.甲、乙两车分别从 、 两地同时出发,沿同一条公路相向而行,相遇时甲、乙所走路程的比为2:3,甲、乙两车离 中点 路程 (千米)与甲车出发时间 (时)的关系图象如图所示,则下列说法错误的是( )
A.乙车的速度为90千米/时
B. 的值为
C. 的值为150
D.当甲、乙车相距30千米时,甲行走了 或
二、填空题
9.已知一次函数y=(m+2)x-5,若y随x的增大而减小,则m的取值范围为 .
10.如图,一次函数与x轴、y轴分别交于A、B两点,则不等式的解集是 .
11.已知一次函数的图象经过点和,则 .
12.一次函数y=2x+4的图象与x轴、y轴的交点分别为A,B,则线段AB的长为 .
13.小明家到学校的路程是米,小明从家出发,以平均每分钟米的速度步行去上学,则他离学校的路程(米)与行走的时间(分)之间的关系式是 .
三、解答题
14.已知与成正比例,且时,.
(1)求与的函数关系式;
(2)将所得函数图象平移,使它过点.求平移后直线的解析式.
15.一条公路上依次有A,C,B三地,甲、乙两车分别从A,B两地同时出发,匀速行驶,甲车驶向C地,乙车从B地驶向C地,停1h后按原速原路返回到B地.两车与C地的距离y(单位:)与甲车出发的时间x(单位:h)之间的函数图象如图所示.
(1)求甲、乙两车的速度;
(2)求乙车从出发到返回B地的过程中y与x之间的函数解析式;
(3)直接写出甲车出发多长时间时,甲、乙两车相距.
16.如图,已知直线经过点,,与直线交于C点、
(1)求直线的解析式以及以与x轴的交点D的坐标;
(2)求C点的坐标;
(3)根据图象,直接写出关于的不等式时x的取值范围.
17.荆州古城旁“荆街”某商铺打算购进A,B两种文创饰品对游客销售.已知1400元采购A种的件数是630元采购B种件数的2倍,A种的进价比B种的进价每件多1元,两种饰品的售价均为每件15元;计划采购这两种饰品共600件,采购B种的件数不低于390件,不超过A种件数的4倍.
(1)求A,B饰品每件的进价分别为多少元?
(2)若采购这两种饰品只有一种情况可优惠,即一次性采购A种超过150件时,A种超过的部分按进价打6折.设购进A种饰品x件,①求x的取值范围;②设计能让这次采购的饰品获利最大的方案,并求出最大利润.
参考答案
1.B
2.A
3.B
4.D
5.D
6.B
7.C
8.D
9.m<-2
10.
11.-6
12.
13.
14.(1)
(2)
15.(1)甲车的速度为,乙车的速度为
(2)
(3)甲车出发或或时,甲、乙两车相距300km
16.(1)解:∵直线y1=kx+b经过点A(5,0),B(1,4)
∴,解得
∴直线AB的解析式为:y1=-x+5;
在y2=2x-4中,令y=0,则x=2
∴y2与x轴的交点D的坐标为(2,0);
(2)接:解得
∴点C坐标为(3,2);
(3)解:由图象可知,不等式时x的取值范围为.
17.(1)解:设A种饰品每件的进价为元,则B种饰品每件的进价为
由题意得: 解得:
经检验,是所列方程的根,且符合题意.
A种饰品每件进价为10元,B种饰品每件进价为9元
(2)解:①根据题意得: 解得:
购进A种饰品件数的取值范围为:
②设采购A种饰品件时的总利润为元.
当时, 即
,随的增大而减小. 当时,有最大值3480.
当时,
整理得: 3>0,随的增大而增大.
当时,有最大值3630.
,w的最大值为3630,此时.
即当采购A种饰品210件,B种饰品390件时,商铺获利最大,最大利润为3630元.
同课章节目录
