有理数的乘法2(浙江省台州市)
文档属性
| 名称 | 有理数的乘法2(浙江省台州市) |  | |
| 格式 | rar | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-09-26 11:43:00 | ||
图片预览


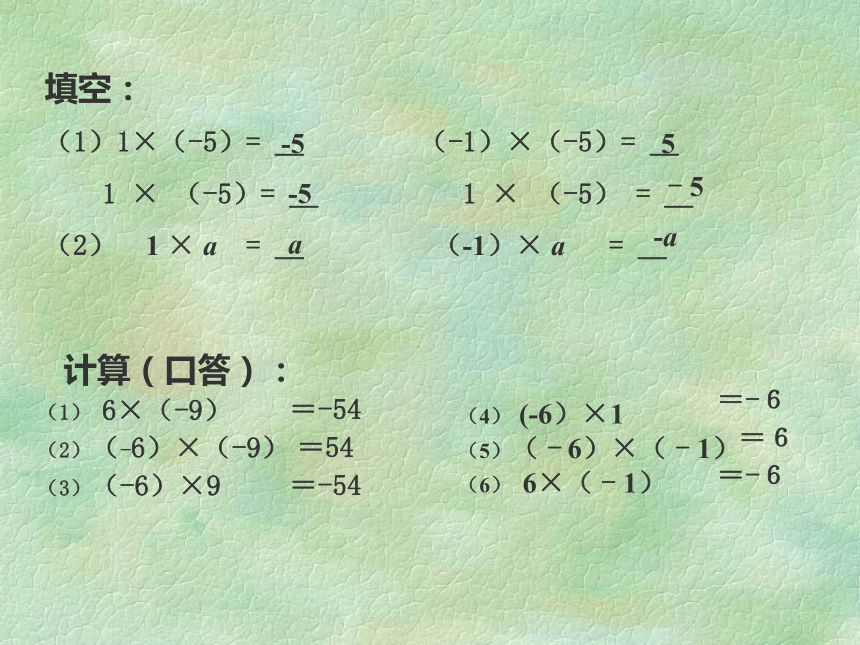


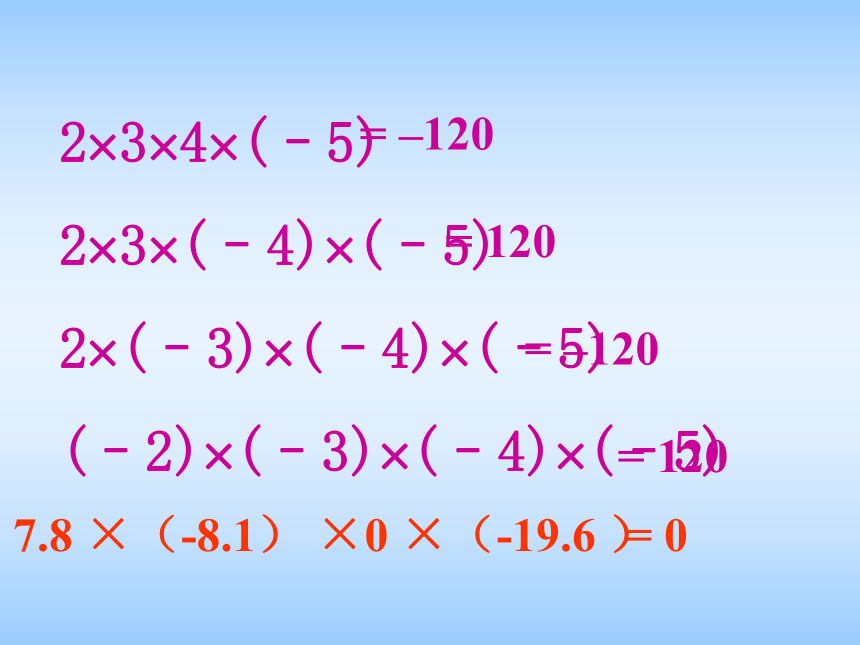
文档简介
课件12张PPT。有理数的乘法2城关中学
陈灵敏1.有理数乘法法则: 两数相乘,同号得正,异号得负,并把绝对值相乘,任何数同0相乘,都得0。2.如何进行两个有理数的运算: 先确定积的符号,再把绝对值相乘,当有一个因数为零时,积为零。复习:=-54
=54
=-54=-6
=6
=-6填空:
(1)1×(-5)= _ (-1)×(-5)= _
1 × (-5)= _ 1 × (-5) = _
(2) 1 × a = _ (-1)× a = _-55-5- 5a-a解:(1) (-3) ×(-9) = 27注意:一个数同+1相乘,得原数,一个数同-1相乘,得原数的相反数。 (3) 7 × (-1) =(4) (-0.8)× 1 = - 7 - 0.8(1)2×3 ×4 ×(-5)
(2)2×3 ×(-4) ×(-5)
(3)2×(-3) ×(-4) ×(-5)
(4)(-2)×(-3) ×(-4 )×(-5)
-+-+判断下列各式的符号:7.8 ×(-8.1) ×0 ×(-19.6 ) ?
2?3?4?(–5)
2?3?(–4)?(–5)
2?(–3)?(–4)?(–5)
(–2)?(–3)?(–4)?(–5)= –120= –120= 120= 1207.8 ×(-8.1) ×0 ×(-19.6 )= 0 几个不等于零的数相乘,积的符号由负因数的个数决定.当负因数有奇数个时,积为负;当负因数有偶数个时,积为正. 几个数相乘,有一个因数为0,积就为0.用“>”、“<”或“=”填空。
(1)(-3)×(-5) ×(-7) ×(-9) 0
(2)(+8.36) ×(+2.9) ×(-7.89) 0
(3)50 ×(-2) ×(-3) ×(-2) ×(-5) 0
(4)(-3) ×(-2) ×(-1) 0
(5)739 ×(-123) ×(-329) ×0 0><><=1.(1)如果2个数的乘积为负数,其中有个 负因数。(2)如果3个数的乘积为负数,其中有个 负因数。(3)如果4个数的乘积为负数,其中有个 负因数。(4)如果5个数的乘积为负数,其中有个 负因数。(5)如果101个数的乘积为负数,其中有个 负因数。11或31或31,3,51,3,…,101思考你能发现其中的规律吗?2003个数的乘积为负数,其中负因数个
数有几种可能?1.用“<”或“>”号填空
(1)如果a<0 b>0那么 ab _ 0
(2)如果a<0 b<0那么 ab _ 0<>2.判断下列方程的解是正数、负数还是0:
(1) 4X= -16 (2)-3X=18
(3)-9X=-36 (4)-5X=03.思考题: (1)当a >0时,a与 2a哪个大?
(2)当a < 0时,a与2a哪个大? 几个不等于0的数相乘,积的符号由负因数的个数决定.当负因数有奇数个时,积为负;当负因数有偶数个时,积为正.
几个数相乘,有一个因数为0,积就为0. 有理数乘法法则
两数相乘,同号得正,异号得负,并把绝对值相乘.
任何数同0相乘,都得0.小结
陈灵敏1.有理数乘法法则: 两数相乘,同号得正,异号得负,并把绝对值相乘,任何数同0相乘,都得0。2.如何进行两个有理数的运算: 先确定积的符号,再把绝对值相乘,当有一个因数为零时,积为零。复习:=-54
=54
=-54=-6
=6
=-6填空:
(1)1×(-5)= _ (-1)×(-5)= _
1 × (-5)= _ 1 × (-5) = _
(2) 1 × a = _ (-1)× a = _-55-5- 5a-a解:(1) (-3) ×(-9) = 27注意:一个数同+1相乘,得原数,一个数同-1相乘,得原数的相反数。 (3) 7 × (-1) =(4) (-0.8)× 1 = - 7 - 0.8(1)2×3 ×4 ×(-5)
(2)2×3 ×(-4) ×(-5)
(3)2×(-3) ×(-4) ×(-5)
(4)(-2)×(-3) ×(-4 )×(-5)
-+-+判断下列各式的符号:7.8 ×(-8.1) ×0 ×(-19.6 ) ?
2?3?4?(–5)
2?3?(–4)?(–5)
2?(–3)?(–4)?(–5)
(–2)?(–3)?(–4)?(–5)= –120= –120= 120= 1207.8 ×(-8.1) ×0 ×(-19.6 )= 0 几个不等于零的数相乘,积的符号由负因数的个数决定.当负因数有奇数个时,积为负;当负因数有偶数个时,积为正. 几个数相乘,有一个因数为0,积就为0.用“>”、“<”或“=”填空。
(1)(-3)×(-5) ×(-7) ×(-9) 0
(2)(+8.36) ×(+2.9) ×(-7.89) 0
(3)50 ×(-2) ×(-3) ×(-2) ×(-5) 0
(4)(-3) ×(-2) ×(-1) 0
(5)739 ×(-123) ×(-329) ×0 0><><=1.(1)如果2个数的乘积为负数,其中有个 负因数。(2)如果3个数的乘积为负数,其中有个 负因数。(3)如果4个数的乘积为负数,其中有个 负因数。(4)如果5个数的乘积为负数,其中有个 负因数。(5)如果101个数的乘积为负数,其中有个 负因数。11或31或31,3,51,3,…,101思考你能发现其中的规律吗?2003个数的乘积为负数,其中负因数个
数有几种可能?1.用“<”或“>”号填空
(1)如果a<0 b>0那么 ab _ 0
(2)如果a<0 b<0那么 ab _ 0<>2.判断下列方程的解是正数、负数还是0:
(1) 4X= -16 (2)-3X=18
(3)-9X=-36 (4)-5X=03.思考题: (1)当a >0时,a与 2a哪个大?
(2)当a < 0时,a与2a哪个大? 几个不等于0的数相乘,积的符号由负因数的个数决定.当负因数有奇数个时,积为负;当负因数有偶数个时,积为正.
几个数相乘,有一个因数为0,积就为0. 有理数乘法法则
两数相乘,同号得正,异号得负,并把绝对值相乘.
任何数同0相乘,都得0.小结
