垂径定理

(共16张PPT)
1、知道圆是轴对称图形，能说出它的对称轴，知道圆又是中心对称图形，它的对称中心是圆心。
2、会用图形语言、文字语言、符号语言表示垂径定理。
3、会用垂径定理解决简单的实际问题。
4、学会用动态的观点研究平面几何的有些问题。
1、举例什么是轴对称图形。
如果一个图形沿一条直线对折，直线两旁的部分能够互相重合，那么这个图形叫轴对称图形。
2、举例什么是中心对称图形。
把一个图形绕着某一个点旋转180 ，如果旋转后的图形能够和原来的图形互相重合，那么这个图形叫做中心对称图形。
线段、角、等腰三角形、矩形、菱形、等腰梯形、正方形
平行四边形、正方形、矩形
3、圆是不是轴对称图形？
演 示
圆是轴对称图形，经过圆心的每一条直线都是它的对称轴。
演 示
演 示
问题：左图中AB为圆O的直径，CD为圆O的弦。相交于点E，当弦CD在圆上运动的过程中有没有特殊情况？
运动CD
直径AB和弦CD互相垂直
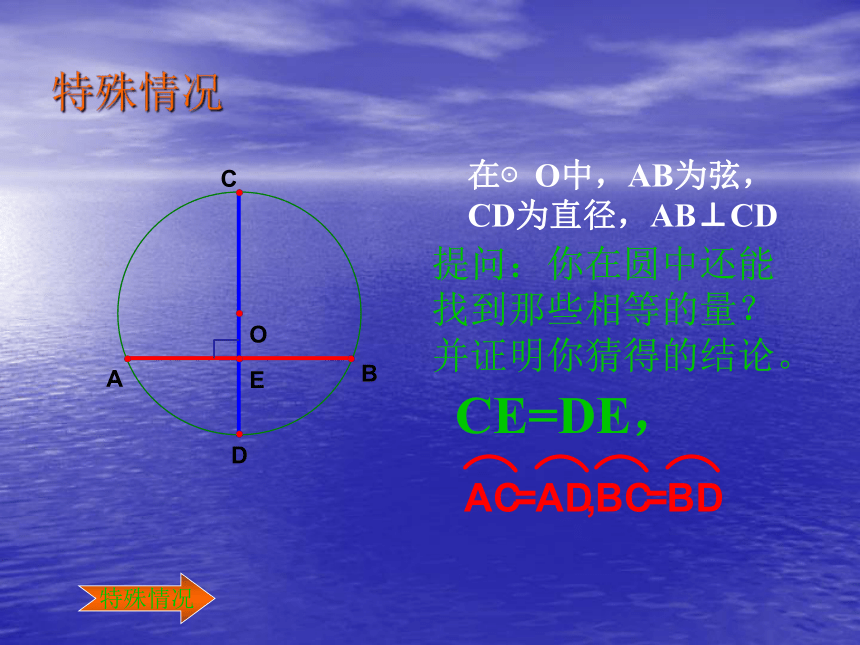
特殊情况
在⊙O中，AB为弦，CD为直径，AB⊥CD
提问：你在圆中还能找到那些相等的量？并证明你猜得的结论。
特殊情况
CE=DE，
证明结论
已知：在⊙O中，CD是直径，AB是弦，CD⊥AB，垂足为E。求证：AE＝BE，AC＝BC，AD＝BD。
⌒
⌒
⌒
⌒
证明：连结OA、OB，则OA＝OB。因为垂直于弦AB的直径CD所在的直线既是等腰三角形OAB的对称轴又是⊙ O的对称轴。所以，当把圆沿着直径CD折叠时，CD两侧的两个半圆重合，A点和B点重合，AE和BE重合，AC、AD分别和BC、 BD重合。因此
AE＝BE，AC＝BC，AD＝BD
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
C
.
O
A
E
B
D
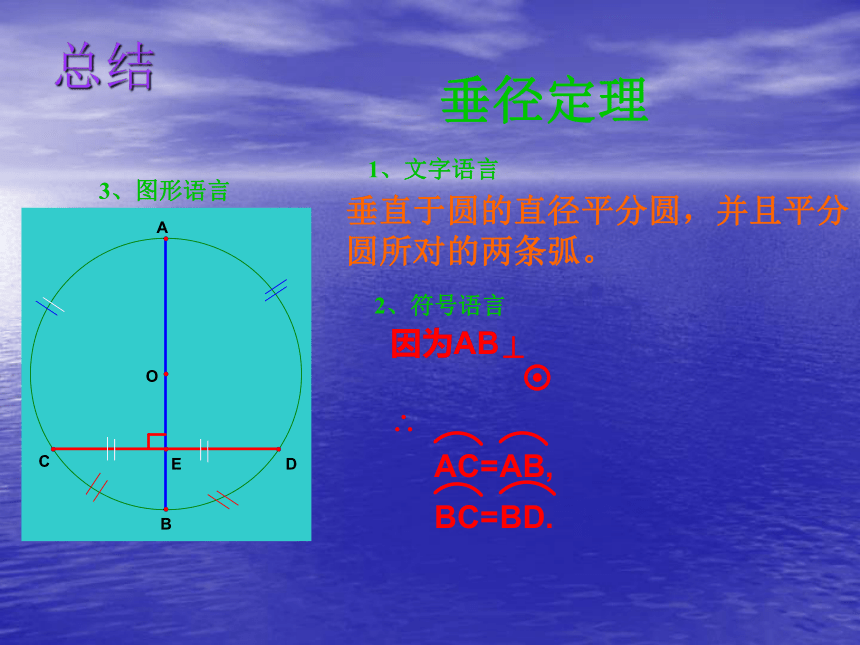
垂径定理
垂直于圆的直径平分圆，并且平分 圆所对的两条弧。
总结
1、文字语言
2、符号语言
3、图形语言
2、请画图说明垂径定理的条件和结论。
1、判断下列图是否是表示垂径定理的图形。
是
不是
是
条件
结论
（1）过圆心
（2）垂直于弦
｝
｛
（3）平分弦
（4）平分弦所对的优弧
（5）平分弦所对的劣弧
分析
CD为直径，
CD⊥AB
｝
｛
点C平分弧
ACB
点D平分弧
ADB
例1 如图，已知在⊙O中，弦AB的长为8厘米，圆心O到AB的距离为3厘米，求⊙O的半径。
则OE＝3厘米，AE＝BE。∵AB＝8厘米 ∴AE＝4厘米
在Rt△AOE中，根据勾股定理有OA＝5厘米 ∴⊙O的半径为5厘米。
.
A
E
B
O
例题1
解：连结OA。过O作OE⊥AB，垂足为E，
例2 已知：如图，在以O为圆心的两个同心圆中，大圆的弦AB交小圆于C，D两点。
求证：AC＝BD。
则AE＝BE，CE＝DE。
AE－CE＝BE－DE。
所以，AC＝BD
E
.
A
C
D
B
O
例题2
证明：过O作OE⊥AB，垂足为E，
┐
例3 已知：⊙O中弦AB∥CD。
求证：AC＝BD
⌒
⌒
∵AB∥CD，∴MN⊥CD。则AM＝BM，CM＝DM（垂直平分弦的直径平分弦所对的弦）
AM－CM＝BM－DM
∴AC＝BD
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
.
M
C
D
A
B
O
N
例题3
证明：作直径MN⊥AB。
课本第69页习题7 .1 A组第11、12、13题本课件是幻灯片+几何画板共同创作的，已经设计好了它们的链接，请把它作为一个整体解压缩到桌面即可使用，谢谢欣赏！欢迎您提出宝贵的修改意见！等候您的赐教！