垂径定理的应用.(河南省新乡市)
文档属性
| 名称 | 垂径定理的应用.(河南省新乡市) |  | |
| 格式 | rar | ||
| 文件大小 | 234.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-09-26 19:23:00 | ||
图片预览


文档简介
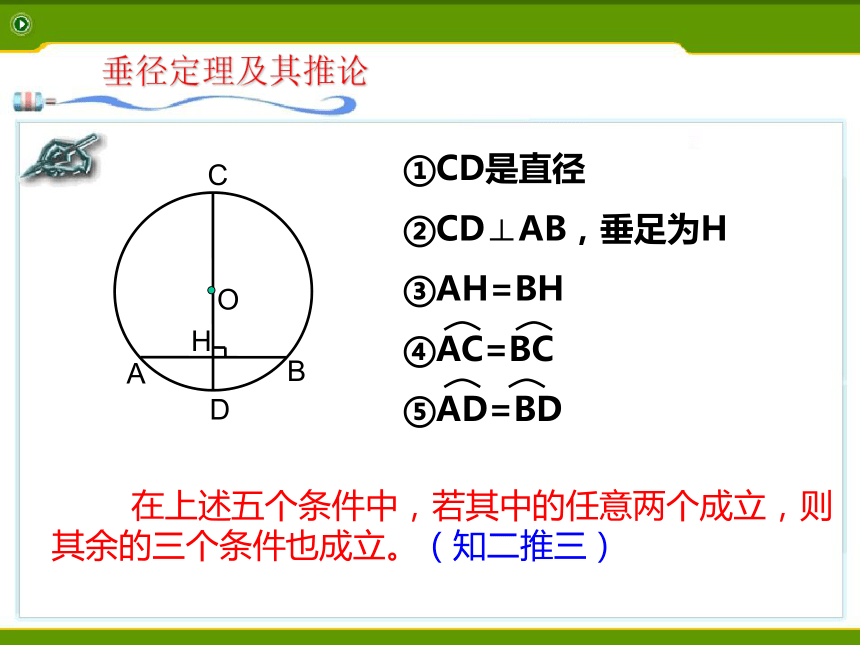
课件15张PPT。垂径定理的应用 在上述五个条件中,若其中的任意两个成立,则
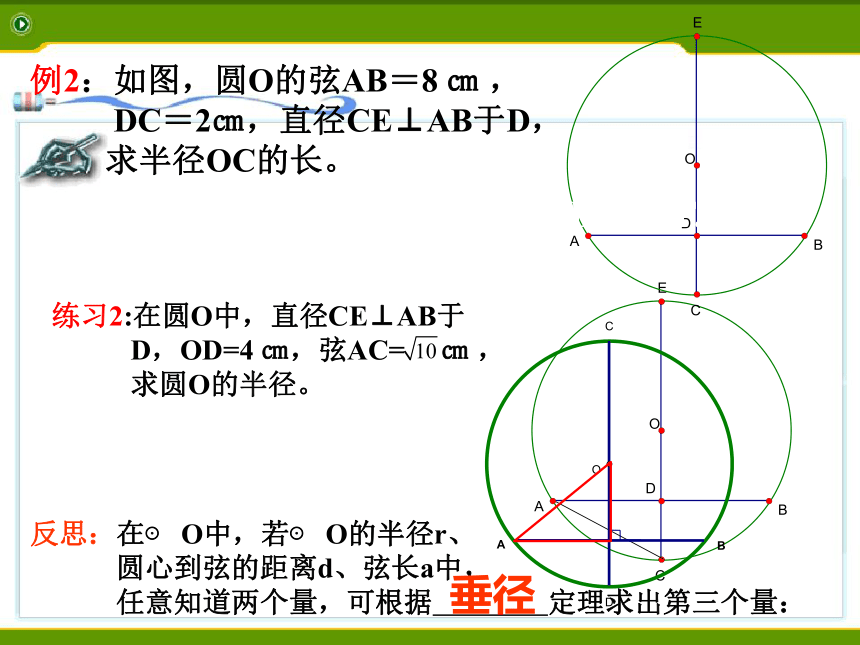
其余的三个条件也成立。(知二推三)垂径定理及其推论例2:如图,圆O的弦AB=8 ㎝ ,
DC=2㎝,直径CE⊥AB于D,
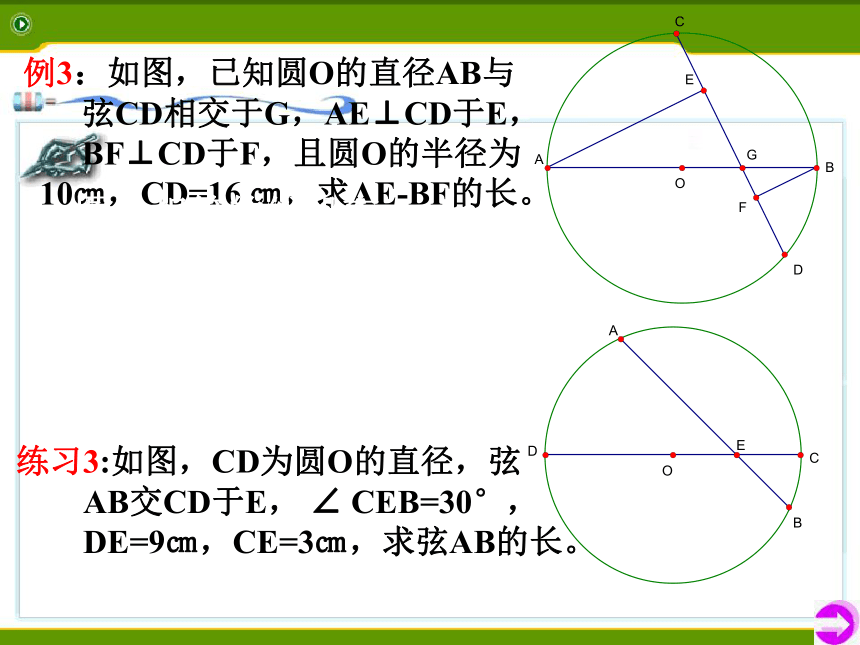
求半径OC的长。垂径直径MN⊥AB,垂足为E,交弦CD于点F.例3:如图,已知圆O的直径AB与
弦CD相交于G,AE⊥CD于E,
BF⊥CD于F,且圆O的半径为
10㎝,CD=16 ㎝,求AE-BF的长。
练习3:如图,CD为圆O的直径,弦
AB交CD于E, ∠ CEB=30°,
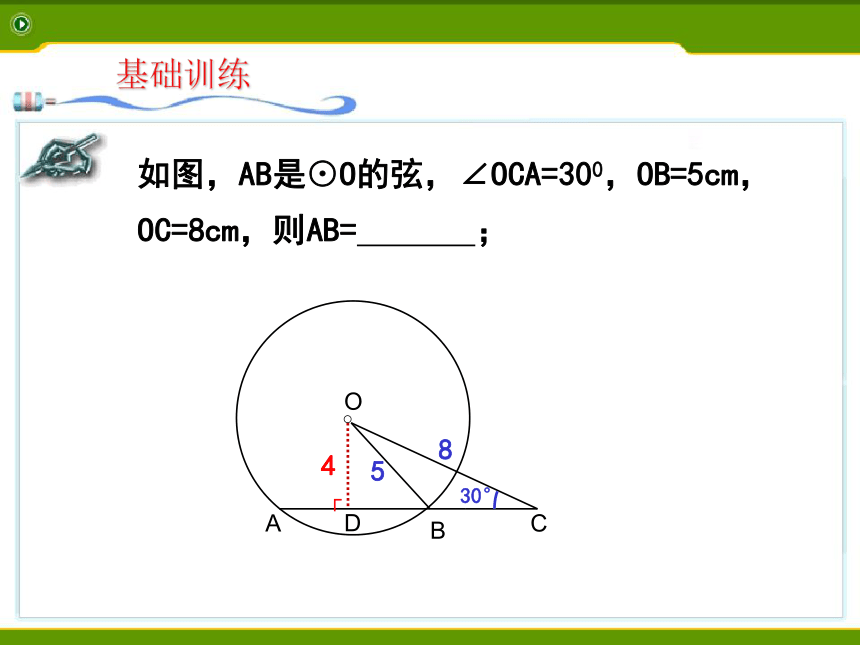
DE=9㎝,CE=3㎝,求弦AB的长。图中相等的线段有 :基础训练如图,AB是⊙O的弦,∠OCA=300,OB=5cm,OC=8cm,则AB= ;OABC30°854EOABDC已知:如图,直径CD⊥AB,垂足为E .
⑴若半径r= 2 ,AB = , 求OE、DE 的长.
⑵若半径r= 2 ,OE = 1 ,求AB、DE 的长.
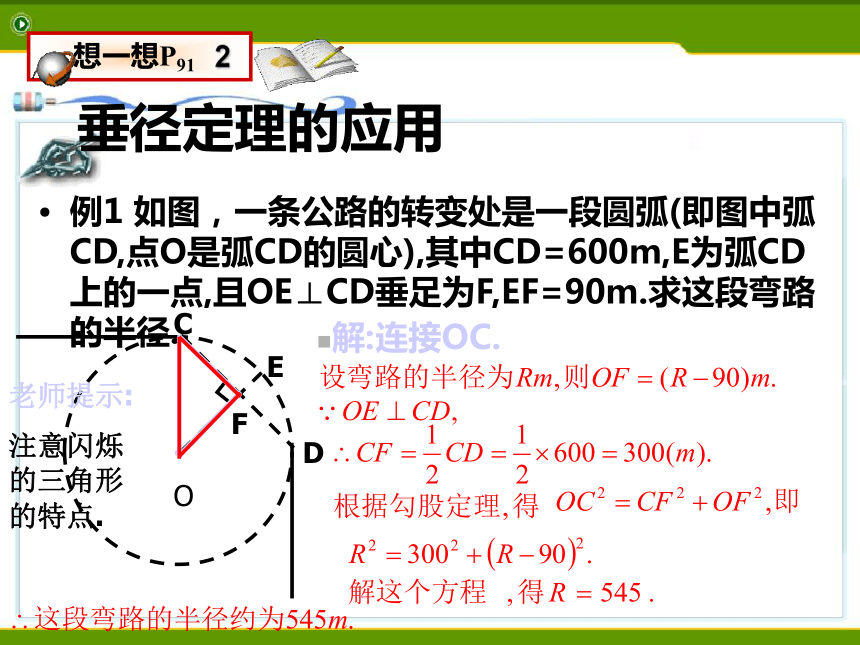
⑶由⑴ 、⑵两题的启发,你还能编出什么其他问题?r⑴d + h = r⑵在a,d,r,h中,已知其中任意两个量,可以求出其它两个量。引例垂径定理的应用例1 如图,一条公路的转变处是一段圆弧(即图中弧CD,点O是弧CD的圆心),其中CD=600m,E为弧CD上的一点,且OE⊥CD垂足为F,EF=90m.求这段弯路的半径.解:连接OC.老师提示:
注意闪烁的三角形的特点. 例、1300多年前,我国隋朝建造的赵州石拱桥(如图)的桥拱是圆弧形,它的跨度(弧所对是弦的长)为 37.4 米,拱高(弧的中点到弦的距离,也叫弓形高)为7.2米,求桥拱的半径(精确到0.1米).ABCD例题解析巩固训练 在直径为650mm的圆柱形油槽内装入一些油后,截面如图所示.若油面宽AB=600mm,求油的最大深度. 一弓形弦长为 cm,弓形所在的圆的半径为7cm,则弓形的高为____. 巩固训练 某地有一座圆弧形的拱桥,桥下的水面宽度为7.2m,拱顶高出水面2.4m,现有一艘宽为3m,船舱顶部为方形并高出水面2米的货船要经过这里,问此货船能顺利通过这座拱桥吗?变式训练船能过拱桥吗解:如图,用 表示桥拱, 所在圆的圆心为O,半径为Rm,
经过圆心O作弦AB的垂线OD,D为垂足,与 相交于点C.根
据垂径定理,D是AB的中点,C是 的中点,CD就是拱高.
由题设得在Rt△OAD中,由勾股定理,得解得 R≈3.9(m).在Rt△ONH中,由勾股定理,得∴此货船能顺利通过这座拱桥.已知:如图,弦AB长为7.2 米,弓形高CD为2.4米;问题:若弦EF=3米,且EF⊥CD于H,计算DH的长变化:若弦EF⊥CD于H,且DH=2米,求EF的长垂径定理的应用小 结 运用垂径定理可以解决许多生产、生活实际问题,其中弓形是最常见的图形(如图),则弦a,弦心距d,弓形高h,半径r之间有以下关系:O d+h=r 垂径定理的应用hrd谢谢大家!
其余的三个条件也成立。(知二推三)垂径定理及其推论例2:如图,圆O的弦AB=8 ㎝ ,
DC=2㎝,直径CE⊥AB于D,
求半径OC的长。垂径直径MN⊥AB,垂足为E,交弦CD于点F.例3:如图,已知圆O的直径AB与
弦CD相交于G,AE⊥CD于E,
BF⊥CD于F,且圆O的半径为
10㎝,CD=16 ㎝,求AE-BF的长。
练习3:如图,CD为圆O的直径,弦
AB交CD于E, ∠ CEB=30°,
DE=9㎝,CE=3㎝,求弦AB的长。图中相等的线段有 :基础训练如图,AB是⊙O的弦,∠OCA=300,OB=5cm,OC=8cm,则AB= ;OABC30°854EOABDC已知:如图,直径CD⊥AB,垂足为E .
⑴若半径r= 2 ,AB = , 求OE、DE 的长.
⑵若半径r= 2 ,OE = 1 ,求AB、DE 的长.
⑶由⑴ 、⑵两题的启发,你还能编出什么其他问题?r⑴d + h = r⑵在a,d,r,h中,已知其中任意两个量,可以求出其它两个量。引例垂径定理的应用例1 如图,一条公路的转变处是一段圆弧(即图中弧CD,点O是弧CD的圆心),其中CD=600m,E为弧CD上的一点,且OE⊥CD垂足为F,EF=90m.求这段弯路的半径.解:连接OC.老师提示:
注意闪烁的三角形的特点. 例、1300多年前,我国隋朝建造的赵州石拱桥(如图)的桥拱是圆弧形,它的跨度(弧所对是弦的长)为 37.4 米,拱高(弧的中点到弦的距离,也叫弓形高)为7.2米,求桥拱的半径(精确到0.1米).ABCD例题解析巩固训练 在直径为650mm的圆柱形油槽内装入一些油后,截面如图所示.若油面宽AB=600mm,求油的最大深度. 一弓形弦长为 cm,弓形所在的圆的半径为7cm,则弓形的高为____. 巩固训练 某地有一座圆弧形的拱桥,桥下的水面宽度为7.2m,拱顶高出水面2.4m,现有一艘宽为3m,船舱顶部为方形并高出水面2米的货船要经过这里,问此货船能顺利通过这座拱桥吗?变式训练船能过拱桥吗解:如图,用 表示桥拱, 所在圆的圆心为O,半径为Rm,
经过圆心O作弦AB的垂线OD,D为垂足,与 相交于点C.根
据垂径定理,D是AB的中点,C是 的中点,CD就是拱高.
由题设得在Rt△OAD中,由勾股定理,得解得 R≈3.9(m).在Rt△ONH中,由勾股定理,得∴此货船能顺利通过这座拱桥.已知:如图,弦AB长为7.2 米,弓形高CD为2.4米;问题:若弦EF=3米,且EF⊥CD于H,计算DH的长变化:若弦EF⊥CD于H,且DH=2米,求EF的长垂径定理的应用小 结 运用垂径定理可以解决许多生产、生活实际问题,其中弓形是最常见的图形(如图),则弦a,弦心距d,弓形高h,半径r之间有以下关系:O d+h=r 垂径定理的应用hrd谢谢大家!
同课章节目录
