数学人教版七年级上册4.3.1 角 优秀教学课件(共29张ppt)
文档属性
| 名称 | 数学人教版七年级上册4.3.1 角 优秀教学课件(共29张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-14 00:00:00 | ||
图片预览




文档简介
(共29张PPT)
第4章 几何图形初步
4.3.1 角
学习目标
1.理解角的有关概念;掌握角的表示方法;
2.能进行度与度、分、秒之间的转化,能够作一个角等于已知角.
剪刀的角
圆规的角
问题背景
楼梯的折角
时针和分针的夹角
问题背景
棱锥上的角
三角尺上的角
问题背景
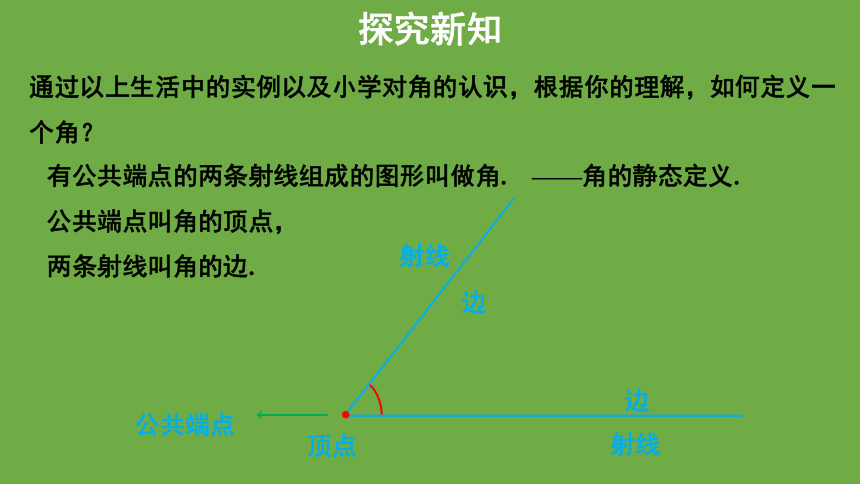
有公共端点的两条射线组成的图形叫做角. ——角的静态定义.
公共端点叫角的顶点,
两条射线叫角的边.
公共端点
顶点
射线
射线
边
边
探究新知
通过以上生活中的实例以及小学对角的认识,根据你的理解,如何定义一个角?
如图
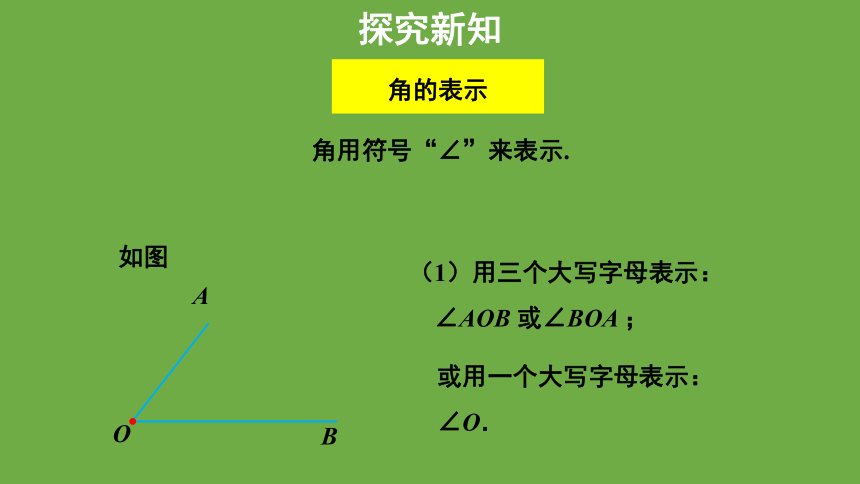
(1)用三个大写字母表示:
∠AOB 或∠BOA ;
A
O
B
或用一个大写字母表示:
∠O.
角用符号“∠”来表示.
探究新知
角的表示
A
O
B
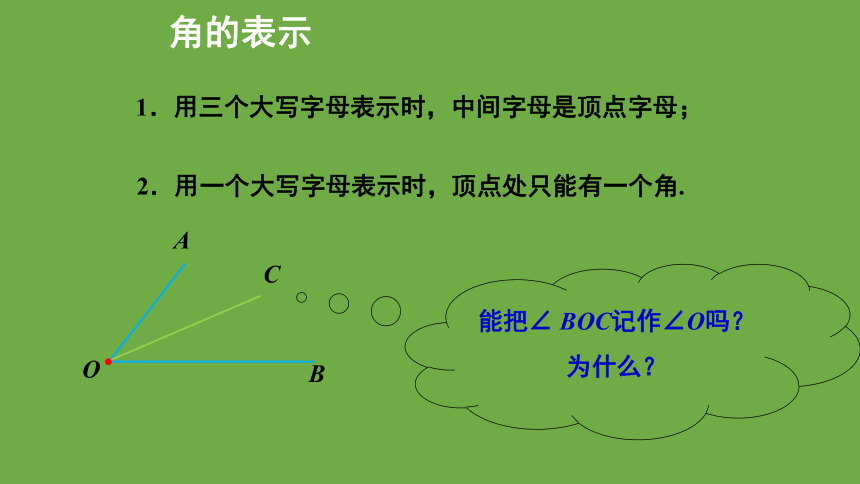
1.用三个大写字母表示时,中间字母是顶点字母;
2.用一个大写字母表示时,顶点处只能有一个角.
C
能把∠ BOC记作∠O吗?为什么?
角的表示
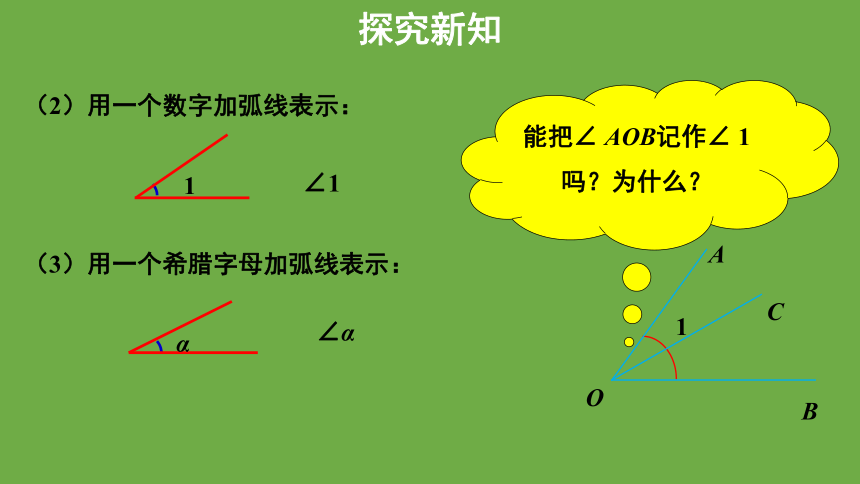
(2)用一个数字加弧线表示:
1
α
(3)用一个希腊字母加弧线表示:
∠1
∠α
A
O
B
C
1
能把∠ AOB记作∠ 1吗?为什么?
探究新知
角的表示方法
(1)用三个大写字母表示:如∠AOB 或∠BOA ;
或用一个大写字母表示:如∠O;
(2)用数字表示:如∠1, ∠2;
(3)用希腊字母表示:如∠α,∠β.
探究新知
角也可以看作由
一条射线绕着它
的端点旋转而
形成的图形.
O
A
B
顶点
射线
探究新知
如图,射线OA绕点O旋转,当终止位置OB和起始位置OA成一条直线时,形成什么角?
(B)
(B)
继续旋转,OB和OA重合时,又形成什么角?
O
A
探究新知
平角:当射线OA绕O点旋转,当终止位置OB与起始位置OA在一条直线上时,形成平角;
周角:当射线OA绕O点旋转,当终止位置OB与起始位置OA重合时,形成周角.
探究新知
平角、周角
角的单位
把一个周角360°等分,每一份就是1度的角,记作1°.除了“度”之外,还有其它的度量单位吗?
1°的 为1分,记作1′,即1°=60′ .
1′的 为1秒,记作1″,即1′=60″ .
角的度、分、秒是60进制的,这和计量时间的时、分、秒是一样的.
探究新知
角的度量工具
量角器
探究新知
如图,已知∠AOB,用量角器量出它的度数.
A
O
B
55°
探究新知
1.对中——角的顶点对准量角器的中心;
3.读数——读出角的另一边所对的度数.
2.重合——角的一边与量角器的零线重合;
用量角器度量角的方法:
探究新知
例1 用度、分、秒表示48.32° .
解:因为0.32°=0.32×60′=19.2′;
0.2′=0.2×60″=12″.
所以48.32°=48°19′12″.
典型例题
例2 用度表示30°9′36〞.
解:因为36〞=36÷60′=0.6′,
9.6′=9.6÷60°=0.16°,
所以30°9′36〞=30.16°.
典型例题
例3. 判断下面各角的表示方法是否正确.
A
B
C
A
B
C
A
B
C
A
B
C
A
B
C
∠ACB
∠B
∠ABC
∠CAB
∠A
( )
( )
( )
( )
( )
×
×
×
√
√
例4. 下面表示∠DEF的图是( )
D
E
F
A
E
D
F
B
D
E
F
C
D
E
F
D
C
典型例题
典型例题
例5.请你把图中用数字表示的角改为用字母表示的角.
解:∠1=∠BAC,∠2=∠B,∠3=∠C,∠4=∠DAC.
典型例题
例6.填空:0.75°=________′=________″;
34.37°=________°________′________″;
1 800″=________°;
39°36′=________°.
45
2700
34
22
12
0.5
39.6
1.已知∠α=18°18′,∠β=18.18°,∠γ=18.3°,下列结论正确的是( ).
A.∠α=∠β B.∠α<∠β C.∠α=∠γ D.∠β>∠γ
C
2.(1)把周角平均分成360份,每份就是_____的角, 1°=_____,
1′=_______.
(2)25.72°=____°____′____″.
(3)15°48′36″=_______°.
(4)3600″=______′=______°.
1度
60′
60″
25
43
12
15.81
60
1
课堂练习
课堂练习
3.(1)下图中表示∠ABC的图是( ).
(2)下列关于角的说法正确的是( ).
A.两条射线组成的图形叫做角
B.延长一个角的两边
C.角的两边是射线,所以角不可以度量
D.角的大小与这个角的两边长短无关
C
D
4.6时整,钟表的时针和分针构成多少度的角?8时呢?8时30分呢?
5.(1)35°等于多少分?等于多少秒?
(2)38°15′和38.15°相等吗?如不相等,哪一个大?
课堂练习
6时整时,时针指6,分针指12,为180°;8时为120°;8时30分为75°.
解:(1)35 °=35 ×60=2100分=126000秒;
(2) 38°15′ =2289分; 38.15°=2295分; 38°15′ >38.15°.
6.从蜂巢的入口处看,蜂巢由许多正六边形(六条边相等,六个角也相等)构成,按图示的方法,利用三角尺和圆规画出一个正六边形.
60°
课堂练习
7.计算:175°16′30″-47°30′÷6+4°12′50″×3.
解:175°16′30″-47°30′÷6+4°12′50″×3
=175°16′30″-2850′÷6+12°36′150″
=175°16′30″-7°55′+12°38′30″
=187°54′60″-7°55′
=180°.
课堂练习
课堂小结
1.角的定义及表示
2.角的单位及换算
3.角的度量
用量角器度量角的方法:
①对中——角的顶点对准量角器的中心;
②重合——角的一边与量角器的零线重合;
③读数——读出角的另一边所对的度数.
再见
第4章 几何图形初步
4.3.1 角
学习目标
1.理解角的有关概念;掌握角的表示方法;
2.能进行度与度、分、秒之间的转化,能够作一个角等于已知角.
剪刀的角
圆规的角
问题背景
楼梯的折角
时针和分针的夹角
问题背景
棱锥上的角
三角尺上的角
问题背景
有公共端点的两条射线组成的图形叫做角. ——角的静态定义.
公共端点叫角的顶点,
两条射线叫角的边.
公共端点
顶点
射线
射线
边
边
探究新知
通过以上生活中的实例以及小学对角的认识,根据你的理解,如何定义一个角?
如图
(1)用三个大写字母表示:
∠AOB 或∠BOA ;
A
O
B
或用一个大写字母表示:
∠O.
角用符号“∠”来表示.
探究新知
角的表示
A
O
B
1.用三个大写字母表示时,中间字母是顶点字母;
2.用一个大写字母表示时,顶点处只能有一个角.
C
能把∠ BOC记作∠O吗?为什么?
角的表示
(2)用一个数字加弧线表示:
1
α
(3)用一个希腊字母加弧线表示:
∠1
∠α
A
O
B
C
1
能把∠ AOB记作∠ 1吗?为什么?
探究新知
角的表示方法
(1)用三个大写字母表示:如∠AOB 或∠BOA ;
或用一个大写字母表示:如∠O;
(2)用数字表示:如∠1, ∠2;
(3)用希腊字母表示:如∠α,∠β.
探究新知
角也可以看作由
一条射线绕着它
的端点旋转而
形成的图形.
O
A
B
顶点
射线
探究新知
如图,射线OA绕点O旋转,当终止位置OB和起始位置OA成一条直线时,形成什么角?
(B)
(B)
继续旋转,OB和OA重合时,又形成什么角?
O
A
探究新知
平角:当射线OA绕O点旋转,当终止位置OB与起始位置OA在一条直线上时,形成平角;
周角:当射线OA绕O点旋转,当终止位置OB与起始位置OA重合时,形成周角.
探究新知
平角、周角
角的单位
把一个周角360°等分,每一份就是1度的角,记作1°.除了“度”之外,还有其它的度量单位吗?
1°的 为1分,记作1′,即1°=60′ .
1′的 为1秒,记作1″,即1′=60″ .
角的度、分、秒是60进制的,这和计量时间的时、分、秒是一样的.
探究新知
角的度量工具
量角器
探究新知
如图,已知∠AOB,用量角器量出它的度数.
A
O
B
55°
探究新知
1.对中——角的顶点对准量角器的中心;
3.读数——读出角的另一边所对的度数.
2.重合——角的一边与量角器的零线重合;
用量角器度量角的方法:
探究新知
例1 用度、分、秒表示48.32° .
解:因为0.32°=0.32×60′=19.2′;
0.2′=0.2×60″=12″.
所以48.32°=48°19′12″.
典型例题
例2 用度表示30°9′36〞.
解:因为36〞=36÷60′=0.6′,
9.6′=9.6÷60°=0.16°,
所以30°9′36〞=30.16°.
典型例题
例3. 判断下面各角的表示方法是否正确.
A
B
C
A
B
C
A
B
C
A
B
C
A
B
C
∠ACB
∠B
∠ABC
∠CAB
∠A
( )
( )
( )
( )
( )
×
×
×
√
√
例4. 下面表示∠DEF的图是( )
D
E
F
A
E
D
F
B
D
E
F
C
D
E
F
D
C
典型例题
典型例题
例5.请你把图中用数字表示的角改为用字母表示的角.
解:∠1=∠BAC,∠2=∠B,∠3=∠C,∠4=∠DAC.
典型例题
例6.填空:0.75°=________′=________″;
34.37°=________°________′________″;
1 800″=________°;
39°36′=________°.
45
2700
34
22
12
0.5
39.6
1.已知∠α=18°18′,∠β=18.18°,∠γ=18.3°,下列结论正确的是( ).
A.∠α=∠β B.∠α<∠β C.∠α=∠γ D.∠β>∠γ
C
2.(1)把周角平均分成360份,每份就是_____的角, 1°=_____,
1′=_______.
(2)25.72°=____°____′____″.
(3)15°48′36″=_______°.
(4)3600″=______′=______°.
1度
60′
60″
25
43
12
15.81
60
1
课堂练习
课堂练习
3.(1)下图中表示∠ABC的图是( ).
(2)下列关于角的说法正确的是( ).
A.两条射线组成的图形叫做角
B.延长一个角的两边
C.角的两边是射线,所以角不可以度量
D.角的大小与这个角的两边长短无关
C
D
4.6时整,钟表的时针和分针构成多少度的角?8时呢?8时30分呢?
5.(1)35°等于多少分?等于多少秒?
(2)38°15′和38.15°相等吗?如不相等,哪一个大?
课堂练习
6时整时,时针指6,分针指12,为180°;8时为120°;8时30分为75°.
解:(1)35 °=35 ×60=2100分=126000秒;
(2) 38°15′ =2289分; 38.15°=2295分; 38°15′ >38.15°.
6.从蜂巢的入口处看,蜂巢由许多正六边形(六条边相等,六个角也相等)构成,按图示的方法,利用三角尺和圆规画出一个正六边形.
60°
课堂练习
7.计算:175°16′30″-47°30′÷6+4°12′50″×3.
解:175°16′30″-47°30′÷6+4°12′50″×3
=175°16′30″-2850′÷6+12°36′150″
=175°16′30″-7°55′+12°38′30″
=187°54′60″-7°55′
=180°.
课堂练习
课堂小结
1.角的定义及表示
2.角的单位及换算
3.角的度量
用量角器度量角的方法:
①对中——角的顶点对准量角器的中心;
②重合——角的一边与量角器的零线重合;
③读数——读出角的另一边所对的度数.
再见
