2023-2024学年北师大版七年级上册 第五章 一元一次方程的应用 【十大类型分类归纳】 (含解析)
文档属性
| 名称 | 2023-2024学年北师大版七年级上册 第五章 一元一次方程的应用 【十大类型分类归纳】 (含解析) | 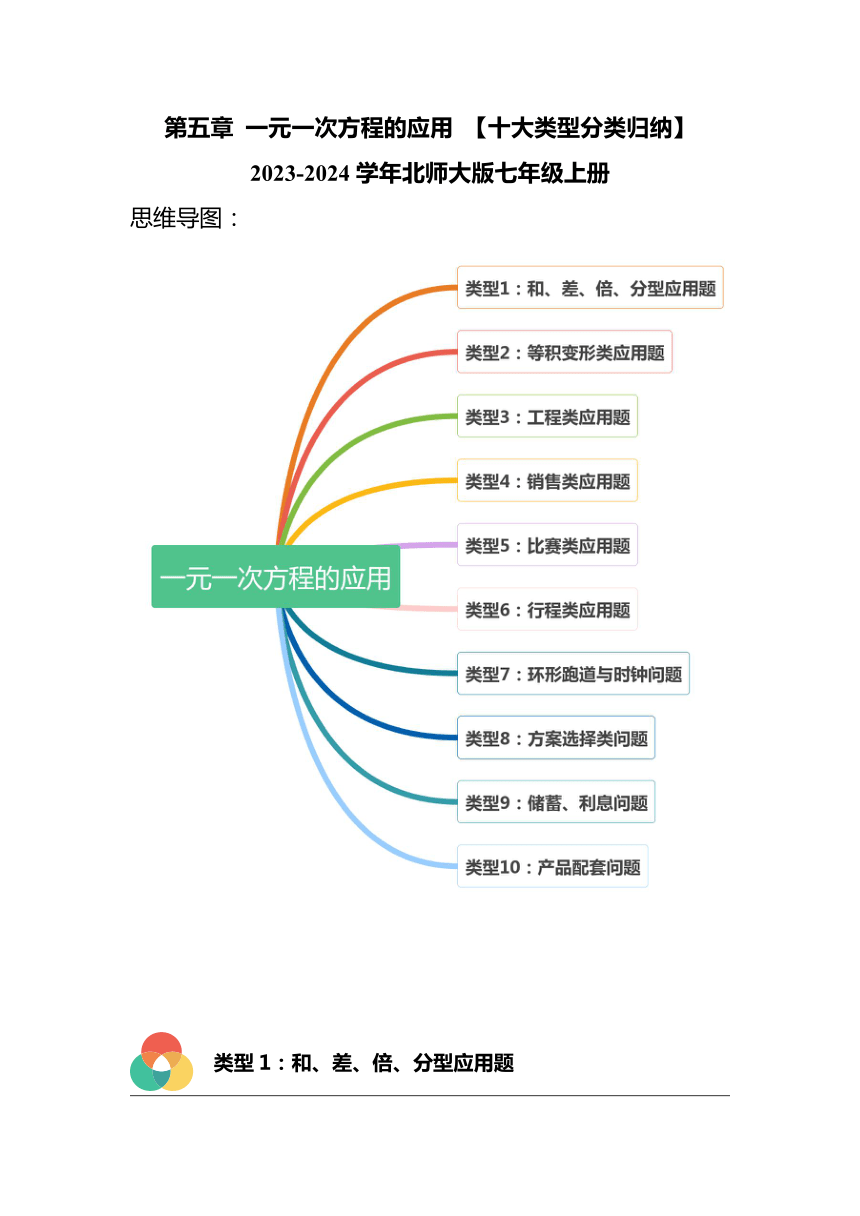 | |
| 格式 | docx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-14 16:49:53 | ||
图片预览




文档简介
第五章 一元一次方程的应用 【十大类型分类归纳】2023-2024学年北师大版七年级上册
思维导图:
类型1:和、差、倍、分型应用题
1.我们定义:如果线段上的一个点将这条线段分成长度分别是,的两部分,并且满足,那么这个点叫做这条线段的“三高四新点”.
(1)如图1,点是线段的“三高四新点”, 且,则 ;
(2)若点也是(1)中线段的“三高四新点”(不同于点),求与的数量关系;
(3)如图2,点是数轴原点,点对应的数是3,点对应的数是12,在点处有一挡板.小球从点出发以每秒1个单位长度的速度向左匀速运动,小球从点同时出发,以每秒3个单位长度的速度向右匀速运动,碰到挡板后立即以每秒3个单位长度的速度向左运动.追上时,两小球同时停止运动.设运动时间为秒,当、、三点中某一点为其余两点所构成线段的“三高四新点”时,请求出的值.
2.学校开展大课间活动,五(1)班有的学生参加了跳绳活动,的同学参加乒乓球活动,剩下的15人全部踢足球,五(1)班共有多少人?
3.如表是两种“优惠套餐”计费方式.(月费固定收,主叫不超时,流量不超量不再收费,主叫超时和上网超流量部分加收超时费和超流量费)
月费(元 主叫(分钟) 流量 接听 超时(元钟) 超流量(元
方式一 49 200 50 免费 0.20 3
方式二 69 250 65 免费 0.15 2
(1)若某月小郭主叫通话时间为320分钟,上网流量为,则她按方式一计费需 元,按方式二计费需 元;若她按方式二计费需119元,主叫通话时间为234分钟,则上网流量为 ;
(2)若上网流量为,是否存在某主叫通话时间(分钟),按方式一和方式二的计费相等?若存在,请求出的值;若不存在,请说明理由.
4.如图,已知在数轴上有、两点,点表示的数是,点表示的数是9.点在数轴上从点出发,以每秒2个单位的速度沿数轴正方向运动,同时,点在数轴上从点出发,以每秒3个单位的速度沿数轴负方向运动,当点到达点时,两点同时停止运动.设运动时间为秒.
(1)求的距离;
(2)当时,点、点分别表示什么数?
(3)当为何值时,、两点相遇?
类型2:等积变形类应用题
5.小林用一根质地均匀的木杆和一些等重的小物体做实验.如图:他在木杆的正中间处栓绳,将木杆吊起来,吊绳处为木杆的支点,记为.然后在木杆的左边挂个重物,在木杆的右边挂个重物,且.并通过移动左右两边的重物直至木杆平衡.记平衡时木杆左边挂重物的位置为,木杆右边挂重物的位置为、多次实验后、小林发现了规律:,即木杆平衡时,左边挂重物的个数支点到木杆左边挂重物处的距离右边挂重物的个数支点到木杆右边挂重物处的距离.
(1)填空: (用含有和的式子表示);
(2)设木杆上中点的位置为.
①若,,,求;
②问:是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
6.有一位工人师傅将底面直径为,高为的实心圆柱,锻造成底面直径为的实心圆柱,求锻造后圆柱的高是多少?
7.将一个底面半径为、高为的“瘦长”圆柱体钢材锻压成底面直径为的“矮胖”圆柱体零件毛坯问:毛坯的高是多少?(列方程解答)
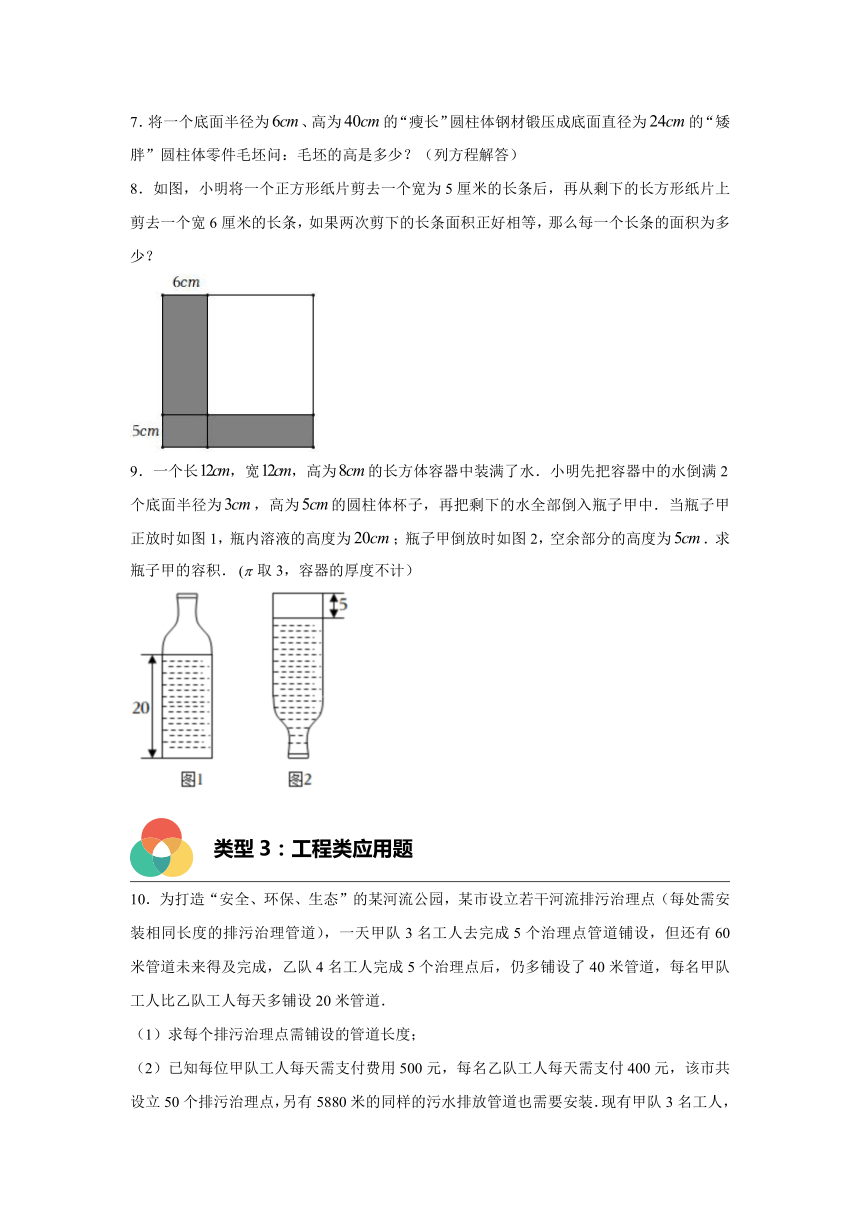
8.如图,小明将一个正方形纸片剪去一个宽为5厘米的长条后,再从剩下的长方形纸片上剪去一个宽6厘米的长条,如果两次剪下的长条面积正好相等,那么每一个长条的面积为多少?
9.一个长,宽,高为的长方体容器中装满了水.小明先把容器中的水倒满2个底面半径为,高为的圆柱体杯子,再把剩下的水全部倒入瓶子甲中.当瓶子甲正放时如图1,瓶内溶液的高度为;瓶子甲倒放时如图2,空余部分的高度为.求瓶子甲的容积.取3,容器的厚度不计)
类型3:工程类应用题
10.为打造“安全、环保、生态”的某河流公园,某市设立若干河流排污治理点(每处需安装相同长度的排污治理管道),一天甲队3名工人去完成5个治理点管道铺设,但还有60米管道未来得及完成,乙队4名工人完成5个治理点后,仍多铺设了40米管道,每名甲队工人比乙队工人每天多铺设20米管道.
(1)求每个排污治理点需铺设的管道长度;
(2)已知每位甲队工人每天需支付费用500元,每名乙队工人每天需支付400元,该市共设立50个排污治理点,另有5880米的同样的污水排放管道也需要安装.现有甲队3名工人,乙队4名工人来安装管道,方案一:全部由甲队安装;方案二:全部由乙队安装;(不到一天按一天算).若要使总费用最少,应选择哪种方案?请通过计算说明.
11.我区某中学举办一年一届的科技文化艺术节活动,需搭建一个舞台,请来两名工人.已知甲单独完成需4小时,乙单独完成需6小时.现由乙提前做1小时,剩下的工作由甲、乙两人合做,问再合做几小时可以完成这项工作?
12.某公司需要加工一批零件,甲每天可以加工16个零件,乙每天可以加工24个零件,甲单独加工这批零件比乙单独加工这批零件多用20天,甲每天的人工费为80元,乙每天的人工费为120元.
(1)问这批零件共有多少个?
(2)在加工零件过程中,公司要派一名质量监督员,并且每天支付他15元补助费,现有三种加工方案:①由甲单独加工这批零件;②由乙单独加工这批零件;③甲、乙合作同时加工这批零件,你认为哪种方案最省钱,为什么?
13.一项工程,甲队单独完成需要40天,乙队单独完成需要50天,现甲队单独做4天后两队合作.
(1)求甲、乙两队合作多少天才能完成该工程.
(2)在(1)的条件下,甲队每天的施工费为3000元,乙队每天的施工费为3500元,求完成此项工程需付给甲乙两队共多少元.
14.甲、乙两队修一座桥,如果由甲队单独完成,需要15天;如果由乙队单独完成,需要30天.现在由甲队单独做了3天后,承办方接到通知,需要加快修桥进度,后续工程由甲、乙两队共同完成,则甲、乙两队后续需要合作多少天才能修完这座桥?
类型4:销售类应用题
15.列方程解决问题:
在“双11”促销活动中,某商场一运动品牌店实施如下调价方案:先把每件商品按原价提价后标价,又以6折销售,一套运动服经过上述调价后售价为270元.
(1)这套运动服的原价为多少元?
(2)在促销活动期间,乐乐妈妈到该品牌店购买了3套该运动服,所花的钱比调价方案前优惠了多少元?
16.小明用的练习本可以到甲、乙两家商店购买,已知两商店的标价都是每本2元,甲商店的优惠条件是购买10本以上,从第11本开始按标价的出售;乙商店的优惠条件是,从第一本起按标价的出售.若小明要购买本练习本.
(1)则当小明到甲商店购买时,需付款 元;当到乙商店购买时,需付款 元;
(2)买多少本练习本时,两家商店花费相同?
(3)小明准备买50本练习本,为了节约开支,选择哪家更划算?
17.忠县重百电商通过互联网销售某品牌电话手表,第一周的总销售额为5520元,第二周的总销售额为6840元,第二周比第一周多售出22块电话手表.
(1)求每块电话手表的售价;
(2)该公司在第三周将每块电话手表的售价降低了,并预计第三周能售出158块电话手表,由于恰逢开学周,不少家庭为子女购买电话手表,该款手表在第三周的销量比预计还多了.如果每块电话手表成本为42元,该公司第三周销售手表的总利润为3318元,求的值.
18.平价商场恰好用3800元购进甲,乙两种商品共50件,若甲种商品每件进价70元,乙种商品每件进价80元,且统一标价120元出售.
(1)求购进甲、乙两种商品各多少件?
(2)该商场售出这批商品的一部分后,恰逢“元旦”对剩余商品进行促销,以标价的8折售完所有剩余商品,共获利1480元,且促销商品中乙的件数是甲件数的1.5倍,求促销商品中甲商品有多少件?
19.“广交会”是中国历史最长的综合性国际贸易盛会.在“广交会”中,某到会采购商计划从厂家购进甲、乙两种商品.已知甲种商品的每件进价比乙种商品的每件进价少20元.若购进甲种商品5件,乙种商品3件,共需要700元.
(1)求甲、乙两种商品的每件进价分别是多少元?
(2)该采购商从厂家购进了甲种商品3万件、乙种商品2万件.在销售时,甲种商品的每件售价为110元,要使得这5万件商品所获利润率为,求每件乙种商品的售价是多少元?
类型5:比赛类应用题
20.为了迎接世界杯足球赛的到来,足球协会举办了一次足球赛,其中得分规则及奖励方案如表:
胜一场 平一场 负一场
积分 3 1 0
人均奖金 1500元 700元 0
当比赛进行到每队比赛完12场时,队共积分20分,并且没有负一场.
(1)试判断队胜、平各几场?
(2)每赛一场,队每名队员均得出场费500元,那么比赛完12场后,队每名队员所得奖金与出场费累计为多少元?
21.在2022年女足亚洲杯决赛中,中国女足以逆转韩国女足,时隔16年再夺亚洲杯冠军!某学校掀起一股足球热,举行了班级联赛,九(1)班开局11场保持不败,共积23分,按照比赛规则,胜一场积3分,平一场积1分,负一场积0分,求该班获胜的场数.
22.篮球运动是最流行的运动之一,深受青少年喜爱.某市举办春季校园篮球赛,共有八支队伍参赛,其中三支队伍的积分表如下.请根据表格信息解答下列问题:
队名 比赛场次 胜场 负场 积分
前进 14 10 4 24
光明 14 9 5 23
远方 14 0 14 14
(1)请回答:胜一场得 分,负一场得 分;
(2)若某队胜场总积分是负场总积分的2倍,求该队的胜场数;
(3)若某队的负场总积分是胜场总积分的正整数倍,求该队的胜场数.
23.在一次知识竞赛中,甲、乙两班各有50位同学参加比赛,每位同学都需要完成三道题的答题,竞赛规则为:“答对一题得10分,不答或者答错扣10分”.
(1)请直接写出每位同学所有可能的得分情况;
(2)甲班的答题情况为:有2位同学全部答错,全对的人数是答对1题人数的3倍少6人,答对两题的人数是答对1题人数的2倍;乙班的答题情况为:没有同学全部答错,答对一题人数的3倍和答对2题的人数之和等于全部答对的人数.
①求甲班全部答对的人数;
②请判断甲乙两班哪个班的得分更高,并说明理由.
24.2022世界杯于11月21日在卡塔尔召开.在小组赛阶段,32支球队根据自身实力所处的不同档次,以及所属大洲的情况进行抽签选择,每个小组4支球队.在小组内部的球队会和其他三支队伍都进行比赛,以下是世界杯小组赛组的积分表.
小组 代表队 场次(场 胜(场 平(场 负(场 积分(分
组 荷兰 3 2 1 0 7
塞内加尔 3 2 0 1 6
厄瓜多尔 3 1 1 1 4
卡塔尔 3 0 0 3 0
(说明:积分胜场积分平场积分负场积分)
(1)求小组赛中胜一场、平一场、负一场各积多少分?
(2)小组赛结束时,阿根廷队没有平场,并且小组赛积分6分,成功晋级,求阿根廷队胜、负各多少场?
(3)在本次小组赛中,能否出现一支球队保持不败的战绩,且胜场总积分恰好等于它的平场总积分?
类型6:行程类应用题
25.甲、乙两队相约沿相同的路线徒步,徒步的路程为,甲队步行速度为,乙队步行速度为,甲队出发后,乙队才出发.
(1)问乙队需要多长时间可以追上甲队;
(2)从甲队出发开始到乙队完成徒步路程止,甲队出发多长时间,两队间隔的路程为.
26.已知数轴上两点、对应的数分别为、4,点为数轴上一动点.
(1)若点到点、点的距离相等,求点对应的数;
(2)数轴上是否存在点,使点到点、点的距离之和为18?若存在,请求出点所表示的数;若不存在,说明理由;
(3)现在点以3个单位长度秒的速度向右运动,点以1个单位长度秒的速度向左运动,点以2个单位长度秒的速度从点向右运动.点、、三点同时运动,当点与点之间的距离为4个单位长度时,求点所对应的数是多少?
27.小明爸爸骑着摩托车带着小明在公路上匀速行驶,如表是小明每隔1小时看到的里程情况,你能确定小明在时看到的里程碑上的数吗?
时间 里程情况
是一个两位数字,它的两个数字之和为7.
十位与个位数字与时所看到的正好颠倒了.
比时看到的两位数中间多了个0.
如果设小明在时看到的数的十位数字是,那么根据以上信息回答下列问题:(结果均要化简)
(1)时小明看到的数可表示为 ;
(2)时小明看到的数可表示为 ,间摩托车行驶的路程是 ;
(3)时小明看到的数可表示为 ,问摩托车行驶的路程是 ;
(4)利用一元一次方程求出小明在时看到的里程碑上的数是多少?
28.如图在数轴上点表示数,点表示数,、满足.
(1)点表示的数为 ;点表示的数为 ;
(2)若在原点处放一挡板,一小球甲从点处以1个单位秒的速度向左运动;同时另一小球乙从点处以3个单位秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为(秒,
①当时,甲小球到原点的距离 ;乙小球到原点的距离 ;
当时,甲小球到原点的距离 ;乙小球到原点的距离 ;
②试探究:甲,乙两小球到原点的距离可能相等吗?若不能,请说明理由若能,请求出甲,乙两小球到原点的距离相等时的值.
③若当甲和乙开始运动时,挡板也从原点以1个单位秒的速度向右运动,直接写出甲,乙两小球到挡板的距离相等时的值.
29.如图,已知线段,点为线段上一点,且.动点以的速度,从点出发,沿方向运动,运动到点停止;点出发后,点以的速度,从点出发,沿方向运动,运动到点时,停留,按原速沿方向运动到点停止.设的运动时间为.
(1) , ;
(2)当从向运动时,若,求的值.
(3)当时,直接写出的值.
类型7:环形跑道与时钟问题
30.钟表是我们日常生活中常用的计时工具.如图,在圆形钟面上,把一周等分成12个大格,每个大格等分成5个小格,分针和时针均绕中心匀速转动.(本题中的角均指小于的角),
(1)分针每分钟转 度,时针每分钟转 度,当时间为时,分针和时针的夹角为 度;
(2)求开始后几分钟分针第一次追上时针;
(3)点为4点钟的位置,平分,平分,从开始计时,分钟后,,求的值.
31.已知环形跑道一圈长为400米,小丽与小杰的速度之比为,如果小丽和小杰在跑道上相距8米处同时反向出发,经过28秒后两人首次相遇,求两人的速度各是多少?
32.周末小明和爸爸在的环形跑道上骑车锻炼,他们在同一地点沿着同一方向同时出发,骑行结束后两人有如下对话:
(1)请根据他们的对话内容,求出小明的骑行速度;
(2)爸爸第一次追上小明后,在第二次相遇前,再经过多少分钟,小明和爸爸在跑道上相距?
33.周末,小明和爸爸在400米的环形跑道上骑车锻炼,他们在同一地点沿着同一方向同时出发,骑行结束后两人有如下对话:
请根据他们的对话内容,求小明和爸爸的骑行速度.
34.正方形的轨道上有两个点甲与乙,开始时甲在处,乙在处,它们沿着正方形轨道顺时针同时出发,甲的速度为每秒,乙的速度为每秒.
已知正方形轨道的边长为,求乙在第5次追上甲时在哪条线段上?
类型8:方案选择类问题
35.永辉超市为春节促销,特推出了两种购物方案.
方案一:非会员购物所有商品价格可获九折优惠;
方案二:如交纳400元会费成为该超市会员,则所有商品价格可获八五折优惠.
(1)以(元表示商品价格,分别用含有的式子表示出两种购物方案中支出金额;
(2)若某人计划在超市购买价格为5800元的电视机一台,请分析选择哪种方案更省钱?
(3)哪种情况下,两种方案的支出金额相同?
36.某校七年级准备观看电影《长津湖》,由各班班长负责买票,每班人数都多于40人,票价每张30元,一班班长问售票员买团体票是否可以优惠,售票员说:40人以上的团体票有两种优惠方案可选择:方案一:全体人员可打8折;方案二:若打9折,有5人可以免票.
(1)若二班有42名学生,则他该选择哪个方案?
(2)一班班长思考一会儿说,我们班无论选择哪种方案要付的钱是一样的,你知道一班有多少人吗?
37.下表是中国电信两种” 套餐”计费方式.(月基本费固定收,主叫不超主叫时间,流量不超上网流量不收费,主叫超时和上网超流量部分加收超时费和超流量费)
月基本费元 主叫通话分钟 上网流量 接听 主叫超时部分(元分钟) 超出流量部分(元
方式一 49 200 500 免费 0.20 0.15
方式二 69 250 600 免费 0.15 0.1
(1)若某月小萱主叫通话时间为220分钟,上网流量为,则她按方式一计费需 元,按方式二计费需 元,所以她应该选择方式 ;
(2)若小萱某月主叫通话时间为100分钟,是否存在某上网流量,按方式一和方式二的计费相等?若存在,请求出的值:若不存在,请说明理由.
(3)若小萱每月主叫通话时间在100分钟以内,要选择更低的计费方式,请你帮助她做出选择,直接写出结果即可.
38.某校体育社团由于报名人数激增,决定从某体育用品店购买若干足球和篮球,用于日常训练.已知每个篮球的价格比每个足球的价格多30元,用900元购买足球的数量是用720元购买篮球数量的2倍.
(1)求篮球和足球的单价各是多少?
(2)根据学生报名情况,社团需一次性购买篮球和足球共80个,且要求购买足球数量不超过篮球数量的请问社团购买多少个篮球时,能使购买费用最少?
39.2021年“双十一”期间,很多国货品牌受到人们的青睐,销量大幅增长.某平台的体育用品旗舰店实行优惠销售,规定如下:对原价160元件的某款运动速干衣和20元双的某款运动棉袜开展促销活动,活动期间向客户提供两种优惠方案.
方案:买一件运动速干衣送一双运动棉袜;
方案:运动速干衣和运动棉袜均按9折付款.
某户外俱乐部准备购买运动速干衣30件,运动棉袜双.
(1)若该户外俱乐部按方案购买,需付款 元(用含的式子表示);若该户外俱乐部按方案购买,需付款 元(用含的式子表示);
(2)若,通过计算说明此时按哪种方案购买较为合算;
(3)当购买运动棉袜多少双时两种方案付款相同.
类型9:储蓄、利息问题
40.小希准备在6年后考上大学时,用15000元给父母买一份礼物表示感谢,决定现在把零花钱存入银行.下面有两种储蓄方案:
①直接存一个6年期.年期年利率为
②先存一个3年期,3年后本金与利息的和再自动转存一个3年期.年期年利率为
你认为按哪种储蓄方案开始存入的本金比较少?请通过计算说明理由.
41.小明的爸爸开了一家运动品商店,近期商店购进一批运动服,按进价提高后打八折出售,这时每套运动服的售价为140元.
(1)求每套运动服的进价?
(2)运动服卖出一半后,正好赶上双十一促销,商店决定将剩下的运动服每3套400元的价格出售,很快销售一空,后一半促销获利5000元,求小明的爸爸共购进多少套运动服?
(3)最后,小明的爸爸决定将整批运动服的利润当做小明的教育基金存入银行,已知该银行3年期的固定储蓄年利率为,求3年后取出的本息和为多少元?
42.妈妈为小华存了一个3年期的教育储蓄(设3年期的年利率为,3年后能取10350元,妈妈开始存入了多少元?
43.小明的爸爸三年前为小明存了一份3000元的教育储蓄.今年到期时取出,得本利和为3243元.请你帮小明算一算这种储蓄的年利率.
44.李明存入银行一笔钱,整存整取3年,年利率,到期后共取出5375元,求李明存入了多少钱?
一 类型10:产品配套问题
45.用白铁皮做罐头盒,每张铁皮可制盒身25个,或制盒底40个,一个盒身与两个盒底配成一套.现在有36张白铁皮,用多少张制盒身,多少张制盒底,可使盒身与盒底正好配套?
46.列方程,解应用题:
新型冠状肺炎疫情正在全球蔓延肆虐,口罩成了人们生活中必不可少的物品,某口罩厂有40名工人,每人每天可以生产1000个口罩面或1200根耳绳.一个口罩面需要配两根耳绳,为使每天生产的口罩面与耳绳刚好配套,应安排多少名工人生产口罩面?
47.疫情防控期间,口罩成为人们生活中必不可少的物品.某口罩厂有87名工人,每人每天可以生产900个口罩面或1100个口罩耳绳,一个口罩面需要配两个耳绳.
(1)为使每天生产的口罩面和口罩耳绳刚好配套,应安排多少名工人生产口罩面?
(2)若该工厂某天生产的口罩面与口罩耳绳刚好配套,设一个成品口罩成本价是元,售价是元,请用含、的式子表示该口罩厂该天生产口罩的利润.
48.用相同规格的正方形硬纸板做成如图1的直三棱柱盒子,每个盒子由3个相同的长方形做侧面和2个相同的正三角形做底面组成,硬纸板按如图2的两种方法裁剪(裁剪后边角料不再利用).
方法:剪出6个侧面;方法:剪出4个侧面和5个底面.
现有19张这种规格的正方形硬纸板,裁剪时张用方法,其余用方法.
(1)用含的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,则能做多少个盒子?
49.在手工制作课上,老师组织七年级(2)班的学生用硬纸制作圆柱形茶叶筒.七年级(2)班共有学生44人,其中男生人数比女生人数少2人,并且每名学生每小时剪筒身50个或剪筒底120个.
(1)七年级(2)班有男生、女生各多少人?
(2)要求一个筒身配两个筒底,为了使每小时剪出的筒身与筒底刚好配套,应该分配多少名学生剪筒身,多少名学生剪筒底?
第五章 一元一次方程的应用 【十大类型分类归纳】2023-2024学年北师大版七年级上册
类型1:和、差、倍、分型应用题
1.我们定义:如果线段上的一个点将这条线段分成长度分别是,的两部分,并且满足,那么这个点叫做这条线段的“三高四新点”.
(1)如图1,点是线段的“三高四新点”, 且,则 7 ;
(2)若点也是(1)中线段的“三高四新点”(不同于点),求与的数量关系;
(3)如图2,点是数轴原点,点对应的数是3,点对应的数是12,在点处有一挡板.小球从点出发以每秒1个单位长度的速度向左匀速运动,小球从点同时出发,以每秒3个单位长度的速度向右匀速运动,碰到挡板后立即以每秒3个单位长度的速度向左运动.追上时,两小球同时停止运动.设运动时间为秒,当、、三点中某一点为其余两点所构成线段的“三高四新点”时,请求出的值.
【答案】(1)7;
(2);
(3)当、、三点中某一点为其余两点所构成线段的“三高四新点”时,的值为1,,,,或.
【分析】(1)根据“三高四新点”的定义即可求解;
(2)根据“三高四新点”的定义即可求解;
(3)根据题意,分三种情况:①当时,点向右运动,再分和;②当时,点向左运动,并且在点的右边,再分和;③当时,点向左运动,并且在点的左边,再分和;根据“三高四新点”的定义列出方程,求解即可.
【解答】解:(1)点是线段的“三高四新点”,
,
,
,
;
故答案为:7;
(2)点也是线段的“三高四新点”(不同于点),
,即,
,
,
,
,
;
(3)①当时,点向右运动,点时线段的“三高四新点”,
此时点表示的数为,点表示的数为,
,,
当时,得,解得:,
当时,得,解得:;
②当时,点向左运动,并且在点的右边,
此时点表示的数为,点表示的数为,
,,
当时,得,解得:,
当时,得,解得:;
③当时,点向左运动,并且在点的左边,
此时点表示的数为,点表示的数为,
,,
当时,得,解得:,
当时,得,解得:;
综上,当、、三点中某一点为其余两点所构成线段的“三高四新点”时,的值为1,,,,或.
2.学校开展大课间活动,五(1)班有的学生参加了跳绳活动,的同学参加乒乓球活动,剩下的15人全部踢足球,五(1)班共有多少人?
【答案】36人.
【分析】设五(1)班共有人,根据“跳绳人数乒乓球人数足球人数总人数“列出方程,求解即可.
【解答】解:设五(1)班共有人,
由题意得,
整理,得,
解得.
答:五(1)班共有36人.
3.如表是两种“优惠套餐”计费方式.(月费固定收,主叫不超时,流量不超量不再收费,主叫超时和上网超流量部分加收超时费和超流量费)
月费(元 主叫(分钟) 流量 接听 超时(元钟) 超流量(元
方式一 49 200 50 免费 0.20 3
方式二 69 250 65 免费 0.15 2
(1)若某月小郭主叫通话时间为320分钟,上网流量为,则她按方式一计费需 133 元,按方式二计费需 元;若她按方式二计费需119元,主叫通话时间为234分钟,则上网流量为 ;
(2)若上网流量为,是否存在某主叫通话时间(分钟),按方式一和方式二的计费相等?若存在,请求出的值;若不存在,请说明理由.
【答案】(1)133,89.5;90;
(2)当分钟时,方式一和方式二的计费相等.
【分析】(1)根据主叫通话时间为320分钟,上网流量为,按表格中数据计算即可;根据主叫通话时间为234分钟,设上网流量为,根据题意列出方程,解方程即可;
(2)分,和三种情况,根据方式一和方式二收费相等列出方程,解方程即可.
【解答】解:(1)按方式一:
(元;
按方式二:
(元;
设上网流量为,
根据题意得:,
解得,
上网流量为,
故答案为:133,89.5;90;
(2)存在.
①当时,由题意得:,即,显然不成立;
②当时,由题意得:
,
解得;
③当时,由题意得:
,
解得,不合题意.
综上所述,当分钟时,方式一和方式二的计费相等.
4.如图,已知在数轴上有、两点,点表示的数是,点表示的数是9.点在数轴上从点出发,以每秒2个单位的速度沿数轴正方向运动,同时,点在数轴上从点出发,以每秒3个单位的速度沿数轴负方向运动,当点到达点时,两点同时停止运动.设运动时间为秒.
(1)求的距离;
(2)当时,点、点分别表示什么数?
(3)当为何值时,、两点相遇?
【答案】(1)15个单位长度;
(2)点表示的数是4,点表示的数是6;
(3)3.
【分析】(1)根据两点间距离的定义解得;
(2)当时,利用路程速度时间分别求得、的长度,然后由数轴的性质解答;
(3)根据线段的和差定义计算即可.
【解答】解:(1).
答:的距离为15个单位长度;
(2)当时,
,.
,.
点表示的数是,点表示的数是6;
(3)根据题意,得,
解得.
答:当时,、两点相遇,
类型2:等积变形类应用题
5.小林用一根质地均匀的木杆和一些等重的小物体做实验.如图:他在木杆的正中间处栓绳,将木杆吊起来,吊绳处为木杆的支点,记为.然后在木杆的左边挂个重物,在木杆的右边挂个重物,且.并通过移动左右两边的重物直至木杆平衡.记平衡时木杆左边挂重物的位置为,木杆右边挂重物的位置为、多次实验后、小林发现了规律:,即木杆平衡时,左边挂重物的个数支点到木杆左边挂重物处的距离右边挂重物的个数支点到木杆右边挂重物处的距离.
(1)填空: (用含有和的式子表示);
(2)设木杆上中点的位置为.
①若,,,求;
②问:是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
【答案】(1);
(2);
(3)是定值,定值为.
【分析】(1)根据小林发现的规律:即可解答;
(2)①设,则,根据,列出方程求得,,根据线段中点性质的,则;
(3)分和两种情况,先分别表示出的长,再表示出,以此即可求解.
【解答】(1)由题意可知,,
;
故答案为:;
设,则,
,
解得:,
,,
为的中点,
,
;
②当时,
,
,
,
当时,
,
,
,
综上,是定值,定值为.
6.有一位工人师傅将底面直径为,高为的实心圆柱,锻造成底面直径为的实心圆柱,求锻造后圆柱的高是多少?
【答案】.
【分析】设锻造后圆柱的高是,根据体积相等得出方程,再求出即可.
【解答】解:设锻造后圆柱的高是,
则,
解得:,
即锻造后圆柱的高是.
7.将一个底面半径为、高为的“瘦长”圆柱体钢材锻压成底面直径为的“矮胖”圆柱体零件毛坯问:毛坯的高是多少?(列方程解答)
【答案】.
【分析】设毛坯的高为,根据圆柱形钢材的体积相等得出方程解答即可.
【解答】解:设毛坯的高为,
根据题意,得.
解得.
答:毛坯的高是.
8.如图,小明将一个正方形纸片剪去一个宽为5厘米的长条后,再从剩下的长方形纸片上剪去一个宽6厘米的长条,如果两次剪下的长条面积正好相等,那么每一个长条的面积为多少?
【答案】每一个长条的面积为.
【分析】设原来正方形纸的边长是,则第一次剪下的长条的长是,宽是,第二次剪下的长条的长是,宽是;然后根据第一次剪下的长条的面积第二次剪下的长条的面积,列出方程,求出的值是多少,即可求出每一个长条面积为多少.
【解答】解:设原来正方形纸的边长是,则第一次剪下的长条的长是,宽是,第二次剪下的长条的长是,宽是,
由题意得:,
解得:,
则.
答:每一个长条的面积为.
9.一个长,宽,高为的长方体容器中装满了水.小明先把容器中的水倒满2个底面半径为,高为的圆柱体杯子,再把剩下的水全部倒入瓶子甲中.当瓶子甲正放时如图1,瓶内溶液的高度为;瓶子甲倒放时如图2,空余部分的高度为.求瓶子甲的容积.取3,容器的厚度不计)
【答案】.
【分析】设瓶子甲的半径为,根据“长方形容器的水圆柱体杯子水瓶子中水”先列出方程,求出瓶子的半径,再计算瓶子甲的容积.
【解答】解:设瓶子甲的半径为,
由题意,得.
当时,,
.
瓶子甲的容积为
.
答:瓶子甲的容积为.
类型3:工程类应用题
10.为打造“安全、环保、生态”的某河流公园,某市设立若干河流排污治理点(每处需安装相同长度的排污治理管道),一天甲队3名工人去完成5个治理点管道铺设,但还有60米管道未来得及完成,乙队4名工人完成5个治理点后,仍多铺设了40米管道,每名甲队工人比乙队工人每天多铺设20米管道.
(1)求每个排污治理点需铺设的管道长度;
(2)已知每位甲队工人每天需支付费用500元,每名乙队工人每天需支付400元,该市共设立50个排污治理点,另有5880米的同样的污水排放管道也需要安装.现有甲队3名工人,乙队4名工人来安装管道,方案一:全部由甲队安装;方案二:全部由乙队安装;(不到一天按一天算).若要使总费用最少,应选择哪种方案?请通过计算说明.
【答案】(1)120米;
(2)应选择方案二.
【分析】(1)设每个排污治理点需铺设的管道长度为米,根据每名甲队工人比乙队工人每天多铺设20米管道,即可得出关于的一元一次方程,解之即可得出结论;
(2)利用工作时间工作总量每队每天完成的工作量,可分别求出选择各方案所需时间,利用总费用每名工人每天所需费用该队人数工作时间,可分别求出选择各方案所需总费用,比较后即可得出结论.
【解答】解:(1)设每个排污治理点需铺设的管道长度为米,
依题意得:,
解得:.
答:每个排污治理点需铺设的管道长度为120米.
(2)选择方案一所需时间为(天,
选择方案一所需总费用为(元;
选择方案二所需时间为(天,(天,
选择方案二所需总费用为(元.
,
若要使总费用最少,应选择方案二.
11.我区某中学举办一年一届的科技文化艺术节活动,需搭建一个舞台,请来两名工人.已知甲单独完成需4小时,乙单独完成需6小时.现由乙提前做1小时,剩下的工作由甲、乙两人合做,问再合做几小时可以完成这项工作?
【答案】2小时.
【分析】设再合做小时可以完成这项工作,根据“甲工作小时的工作量乙工作小时的工作量总工作量”列方程求解.
【解答】解:设再合做小时可以完成这项工作,根据题意,得:
,
解得:,
答:还需2小时可以完成这项工作.
12.某公司需要加工一批零件,甲每天可以加工16个零件,乙每天可以加工24个零件,甲单独加工这批零件比乙单独加工这批零件多用20天,甲每天的人工费为80元,乙每天的人工费为120元.
(1)问这批零件共有多少个?
(2)在加工零件过程中,公司要派一名质量监督员,并且每天支付他15元补助费,现有三种加工方案:①由甲单独加工这批零件;②由乙单独加工这批零件;③甲、乙合作同时加工这批零件,你认为哪种方案最省钱,为什么?
【答案】(1)960个;(2)方案③.
【分析】(1)设乙单独加工这批零件用天,则甲单独加工这批零件用天,根据此等量关系列出方程求解即可;
(2)应分为三种情况讨论:①由甲单独加工;②由乙单独加工;③由两人共同加工,分别比较三种情况下,所耗时间和花费金额,求出即省钱,又省时间的加工方案.
【解答】解:(1)设乙单独加工这批零件用天,则甲单独加工这批零件用天,
依题意得:,
解得:,
(个,
答:这批零件共有960个;
(2)方案③最省钱,理由如下:
方案①所需费用:(元,
方案②所需费用:(元,
方案③所需工作天数为:天,所需费用为:(元.
选择方案③最省钱.
13.一项工程,甲队单独完成需要40天,乙队单独完成需要50天,现甲队单独做4天后两队合作.
(1)求甲、乙两队合作多少天才能完成该工程.
(2)在(1)的条件下,甲队每天的施工费为3000元,乙队每天的施工费为3500元,求完成此项工程需付给甲乙两队共多少元.
【答案】(1)20天;
(2)142000元.
【分析】(1)设甲、乙两队合作天才能完成该工程,根据总工程量甲单独做4天完成的部分甲、乙合作完成的部分即可得出关于的一元一次方程,解之即可得出结论;
(2)根据总费用单天费用工作时间即可算出甲、乙两队的费用,将其相加即可得出结论.
【解答】解:(1)设甲、乙两队合作天才能完成该工程,
根据题意得:,
解得:.
答:甲、乙两队合作20天才能完成该工程;
(2)甲队的费用为(元,
乙队的费用为(元,
(元.
答:完成此项工程需付给甲乙两队共142000元.
14.甲、乙两队修一座桥,如果由甲队单独完成,需要15天;如果由乙队单独完成,需要30天.现在由甲队单独做了3天后,承办方接到通知,需要加快修桥进度,后续工程由甲、乙两队共同完成,则甲、乙两队后续需要合作多少天才能修完这座桥?
【答案】甲、乙两队后续需要合作8天才能修完这座桥.
【分析】利用甲队单独完成需要15天,乙队单独完成需要30天,可得出每天完成的工作量份数,进而利用总工作量为1得出等式求出答案.
【解答】解:设甲、乙两队合作完成还需要的天数是,根据题意可得:
.
解得:.
答:甲、乙两队后续需要合作8天才能修完这座桥.
类型4:销售类应用题
15.列方程解决问题:
在“双11”促销活动中,某商场一运动品牌店实施如下调价方案:先把每件商品按原价提价后标价,又以6折销售,一套运动服经过上述调价后售价为270元.
(1)这套运动服的原价为多少元?
(2)在促销活动期间,乐乐妈妈到该品牌店购买了3套该运动服,所花的钱比调价方案前优惠了多少元?
【答案】(1)300元;
(2)90元.
【分析】(1)设这套运动服的原价为元,根据调价后售价为270元,可得出关于的一元一次方程,解之即可得出结论;
(2)利用节省的钱数每套节省的钱数购买数量,即可求出结论.
【解答】解:(1)设这套运动服的原价为元,
根据题意得:,
解得:.
答:这套运动服的原价为300元;
(2)
(元.
答:所花的钱比调价方案前优惠了90元.
16.小明用的练习本可以到甲、乙两家商店购买,已知两商店的标价都是每本2元,甲商店的优惠条件是购买10本以上,从第11本开始按标价的出售;乙商店的优惠条件是,从第一本起按标价的出售.若小明要购买本练习本.
(1)则当小明到甲商店购买时,需付款 元;当到乙商店购买时,需付款 元;
(2)买多少本练习本时,两家商店花费相同?
(3)小明准备买50本练习本,为了节约开支,选择哪家更划算?
【答案】(1),;
(2)30本;
(3)选择甲商店更划算.
【分析】(1)利用总价单价数量,结合两家商店给出的优惠条件,即可用含的代数式表示出到两家商店购买所需费用;
(2)根据两家商店花费相同,即可得出关于的一元一次方程,解之即可得出结论;
(3)分别将代入和中可求出到两家商店购买所需费用,比较后即可得出结论.
【解答】解:(1)依题意得:小明到甲商店购买需付款(元;
小明到乙商店购买需付款(元.
故答案为:;.
(2)依题意得:,
解得:.
答:买30本练习本时,两家商店花费相同.
(3)当时,;
当时,.
,
选择甲商店更划算.
17.忠县重百电商通过互联网销售某品牌电话手表,第一周的总销售额为5520元,第二周的总销售额为6840元,第二周比第一周多售出22块电话手表.
(1)求每块电话手表的售价;
(2)该公司在第三周将每块电话手表的售价降低了,并预计第三周能售出158块电话手表,由于恰逢开学周,不少家庭为子女购买电话手表,该款手表在第三周的销量比预计还多了.如果每块电话手表成本为42元,该公司第三周销售手表的总利润为3318元,求的值.
【答案】(1)每块电话手表的售价为60元;
(2)的值为25.
【分析】(1)设每块电话手表的售价为元,利用总销售额销售单价销售数量,结合第一周及第二周总销售额及销售数量间的关系,可得出关于的一元一次方程,解之即可得出结论;
(2)利用总利润每块电话手表的销售利润第三周的销售数量,可得出关于的一元一次方程,解之即可得出的值.
【解答】解:(1)设每块电话手表的售价为元,
根据题意得:,
解得:.
答:每块电话手表的售价为60元;
(2)根据题意得:,
整理得:,
解得:.
答:的值为25.
18.平价商场恰好用3800元购进甲,乙两种商品共50件,若甲种商品每件进价70元,乙种商品每件进价80元,且统一标价120元出售.
(1)求购进甲、乙两种商品各多少件?
(2)该商场售出这批商品的一部分后,恰逢“元旦”对剩余商品进行促销,以标价的8折售完所有剩余商品,共获利1480元,且促销商品中乙的件数是甲件数的1.5倍,求促销商品中甲商品有多少件?
【答案】(1)购进甲种商品20件,乙种商品30件;
(2)促销商品中甲商品有12件.
【分析】(1)设购进甲种商品件,则购进乙种商品件,利用总价单价数量,可得出关于的一元一次方程,解之可得出购进甲种商品的数量,再将其代入中,即可求出购进乙种商品的数量;
(2)设促销商品中甲商品有件,则乙商品有件,利用总利润销售单价销售数量进货总价,可得出关于的一元一次方程,解之即可得出结论.
【解答】解:(1)设购进甲种商品件,则购进乙种商品件,
根据题意得:,
解得:,
.
答:购进甲种商品20件,乙种商品30件;
(2)设促销商品中甲商品有件,则乙商品有件,
根据题意得:,
解得:.
答:促销商品中甲商品有12件.
19.“广交会”是中国历史最长的综合性国际贸易盛会.在“广交会”中,某到会采购商计划从厂家购进甲、乙两种商品.已知甲种商品的每件进价比乙种商品的每件进价少20元.若购进甲种商品5件,乙种商品3件,共需要700元.
(1)求甲、乙两种商品的每件进价分别是多少元?
(2)该采购商从厂家购进了甲种商品3万件、乙种商品2万件.在销售时,甲种商品的每件售价为110元,要使得这5万件商品所获利润率为,求每件乙种商品的售价是多少元?
【答案】(1)甲种商品的进价80元,则乙种商品的进价100元.
(2)每件乙种商品的售价是121元.
【分析】(1)设甲种商品的进价元,则乙种商品的进价元,根据“购进甲种商品5件,乙种商品3件,共需要700元”可列出方程,求解即可;
(2)设乙种商品的售价为元,根据“使得这5万件商品所获利润率为”列出方程,求解即可.
【解答】解:(1)设甲种商品的进价元,则乙种商品的进价元,
根据题意,得.
解得.
则.
答:甲种商品的进价80元,则乙种商品的进价100元;
(2)设乙种商品的售价为元,
根据题意,得.
解得.
答:每件乙种商品的售价是121元.
类型5:比赛类应用题
20.为了迎接世界杯足球赛的到来,足球协会举办了一次足球赛,其中得分规则及奖励方案如表:
胜一场 平一场 负一场
积分 3 1 0
人均奖金 1500元 700元 0
当比赛进行到每队比赛完12场时,队共积分20分,并且没有负一场.
(1)试判断队胜、平各几场?
(2)每赛一场,队每名队员均得出场费500元,那么比赛完12场后,队每名队员所得奖金与出场费累计为多少元?
【答案】(1)队胜4场,平8场;
(2)出场费加奖金一共17600元.
【分析】(1)设队胜利场,则平了场,根据总积分为20分列出方程即可求解;
(2)根据(1)中求得胜场数和平场数计算每名队员的奖金和出场费的总和即可解题.
【解答】解:(1)设队胜利场,
一共打了12场,
平了场,
,
解得:,(场.
答:队胜4场,平8场.
(2)每场比赛出场费500元,12场比赛出场费共6000元,
赢了4场,奖金为元,
平了8场,奖金为元,
奖金加出场费一共17600元;
答:一共赢了4场,出场费加奖金一共17600元.
21.在2022年女足亚洲杯决赛中,中国女足以逆转韩国女足,时隔16年再夺亚洲杯冠军!某学校掀起一股足球热,举行了班级联赛,九(1)班开局11场保持不败,共积23分,按照比赛规则,胜一场积3分,平一场积1分,负一场积0分,求该班获胜的场数.
【答案】6场.
【分析】设九(1)班获胜场,则平场,根据九(1)班开局11场共积23分,即可得出关于的一元一次方程,解之即可得出结论.
【解答】解:设九(1)班获胜场,则平场,
根据题意得:,
解得:.
答:九(1)班获胜6场.
22.篮球运动是最流行的运动之一,深受青少年喜爱.某市举办春季校园篮球赛,共有八支队伍参赛,其中三支队伍的积分表如下.请根据表格信息解答下列问题:
队名 比赛场次 胜场 负场 积分
前进 14 10 4 24
光明 14 9 5 23
远方 14 0 14 14
(1)请回答:胜一场得 2 分,负一场得 分;
(2)若某队胜场总积分是负场总积分的2倍,求该队的胜场数;
(3)若某队的负场总积分是胜场总积分的正整数倍,求该队的胜场数.
【答案】(1)2,1;
(2)能,胜7场;
(3)2场.
【分析】(1)设胜一场积分,则负一场积分,依照光明队的胜负场次及得分情况可列出一元一次方程,求解即可;
(2)设胜场数是,负场数是,结合(1)中结论,根据胜场总积分是负场总积分的2倍,列一元一次方程求解即可;
(3)设胜场数是,负场数是,列方程解出,根据数的整除特性及奇偶性可得答案.
【解答】解:(1)设胜一场积分,则负一场积分,
依题意得:,
解得,
此时,
胜一场积2分,负一场积1分.
故答案为:2,1;
(2)答:能.理由如下:
设胜场数是,负场数是,
依题意得:,
解得,
1,,
答:该队胜7场;
(3)设胜场数是,负场数是,
依题意得:,
解得:,
是正整数,是奇数,
符合题意的有:,,.
答:该队胜的场数是2场.
23.在一次知识竞赛中,甲、乙两班各有50位同学参加比赛,每位同学都需要完成三道题的答题,竞赛规则为:“答对一题得10分,不答或者答错扣10分”.
(1)请直接写出每位同学所有可能的得分情况;
(2)甲班的答题情况为:有2位同学全部答错,全对的人数是答对1题人数的3倍少6人,答对两题的人数是答对1题人数的2倍;乙班的答题情况为:没有同学全部答错,答对一题人数的3倍和答对2题的人数之和等于全部答对的人数.
①求甲班全部答对的人数;
②请判断甲乙两班哪个班的得分更高,并说明理由.
【答案】(1)分、分、10分和30分;
(2)①21人;
②乙班得分高.
【分析】(1)根据竞赛的得分规则可得答案;
(2)①设甲班答对1题的有人,根据题意列出方程,解方程可得答案;
②首先算出甲班的得分,设乙班全部答对的有人,答对1题的有人,答对2题的有人,整理可得乙班的得分,再比较可得结论.
【解答】解:(1)若只答对1题,则不答或答错2题,得分为:,
若只答对2题,则不答或答错1题,得分为:,
若只答对3题,得分为:,
若不答或答错3题,得分为:,
答:每位同学所有可能的得分情况是分、分、10分和30分;
(2)①设甲班答对1题的有人,
由题意得,,
解得,
(人,
答:甲班全部答对的人数是21人;
②乙班得分更高.
由题意得,甲班答对3题有21人,答对2题的有18人,答对1题的有9人,全部答错的有2人,
故甲班的得分为(分,
设乙班全部答对的有人,答对1题的有人,答对2题的有人,
所以,
即,
故乙班得分为(分,
,
答:乙班得分更高.
24.2022世界杯于11月21日在卡塔尔召开.在小组赛阶段,32支球队根据自身实力所处的不同档次,以及所属大洲的情况进行抽签选择,每个小组4支球队.在小组内部的球队会和其他三支队伍都进行比赛,以下是世界杯小组赛组的积分表.
小组 代表队 场次(场 胜(场 平(场 负(场 积分(分
组 荷兰 3 2 1 0 7
塞内加尔 3 2 0 1 6
厄瓜多尔 3 1 1 1 4
卡塔尔 3 0 0 3 0
(说明:积分胜场积分平场积分负场积分)
(1)求小组赛中胜一场、平一场、负一场各积多少分?
(2)小组赛结束时,阿根廷队没有平场,并且小组赛积分6分,成功晋级,求阿根廷队胜、负各多少场?
(3)在本次小组赛中,能否出现一支球队保持不败的战绩,且胜场总积分恰好等于它的平场总积分?
【答案】(1)胜一场积3分,平一场积1分,负一场积0分;
(2)胜2场,负1场;
(3)不能出现一支球队保持不败的战绩,且胜场总积分恰好等于它的平场总积分.
【分析】(1)根据表格数据,可得负一场积0分,然后设胜一场积分,平一场积分,列方程即可解答;
(2)设阿根廷队胜场,则负场,根据题意列方程即可解答;
(3)设一个队胜场,则平场,根据题意列方程即可解答.
【解答】解:(1)观察积分表,从卡塔尔一行数据可以看出:负一场积0分,
设胜一场积分,从塞内加尔一行数据可得:
,
解得:,
设平一场积分,从荷兰一行数据可得:
,
解得:,
所以,小组赛中胜一场积3分,平一场积1分,负一场积0分,
答:小组赛中胜一场积3分、平一场积1分、负一场积0分;
(2)设阿根廷队胜场,则负场,由题意得:
,
解得:,
(场,
答:阿根廷队胜2场,负1场;
(3)设一个队胜场,则平场,由题意可知,胜场总积分等于平场总积分,得方程:
,
解得:,
(胜场数)的值必须为整数,
不合实际.
答:不能出现一支球队保持不败的战绩,且胜场总积分恰好等于它的平场总积分.
类型6:行程类应用题
25.甲、乙两队相约沿相同的路线徒步,徒步的路程为,甲队步行速度为,乙队步行速度为,甲队出发后,乙队才出发.
(1)问乙队需要多长时间可以追上甲队;
(2)从甲队出发开始到乙队完成徒步路程止,甲队出发多长时间,两队间隔的路程为.
【答案】(1)2小时;
(2)小时或2小时或4小时.
【分析】(1)设小时后乙队可以追上甲队,根据路程相等列方程求解即可;
(2)分追上甲队前和追上甲队后相距两种情况,分别列方程求解即可.
【解答】解:(1)设小时后乙队可以追上甲队,
根据题意得,,
解得,
答:2小时后乙队可以追上甲队;
(2)设甲队出发小时,两队间隔的路程为,
①乙未出发前,根据题意得,,
解得,
②甲乙均出发且未相遇,根据题意得,,
解得,
③甲乙均出发且相遇后,根据题意得,,
解得,
答:甲队出发小时或2小时或4小时,两队间隔的路程为.
26.已知数轴上两点、对应的数分别为、4,点为数轴上一动点.
(1)若点到点、点的距离相等,求点对应的数;
(2)数轴上是否存在点,使点到点、点的距离之和为18?若存在,请求出点所表示的数;若不存在,说明理由;
(3)现在点以3个单位长度秒的速度向右运动,点以1个单位长度秒的速度向左运动,点以2个单位长度秒的速度从点向右运动.点、、三点同时运动,当点与点之间的距离为4个单位长度时,求点所对应的数是多少?
【答案】(1)点对应的数为;
(2)点对应的数为8或;
(3)点对应的数为3或7.
【分析】(1)点到点、点的距离相等,即点为线段的中点,以此即可求解;
(2)设点对应的数为,分两种情况:①当点在点的右侧时,根据两点间距离公式列出方程求解;②当点在点的左侧时,根据两点间距离公式列出方程求解;
(3)设运动时间为秒,分两种情况:①当点在点左侧,点与点之间的距离为4个单位长度时;②当点在点右侧,点与点之间的距离为4个单位长度时;分别列出方程,求解即可.
【解答】解:(1)点到点、点的距离相等,
点为线段的中点,
点对应的数为:;
(2)设点对应的数为,
①当点在点的右侧时,
根据题意得:,
解得:,
②当点在点的左侧时,
根据题意得:,
解得:,
综上,点对应的数为8或;
(3)设运动时间为秒,则点对应的数为,点对应的数为,点对应的数为,
①当点在点左侧,点与点之间的距离为4个单位长度时,
,
解得:,
此时,点对应的数为,
②当点在点右侧,点与点之间的距离为4个单位长度时,
,
解得:,
此时,点对应的数为,
综上,点对应的数为3或7.
27.小明爸爸骑着摩托车带着小明在公路上匀速行驶,如表是小明每隔1小时看到的里程情况,你能确定小明在时看到的里程碑上的数吗?
时间 里程情况
是一个两位数字,它的两个数字之和为7.
十位与个位数字与时所看到的正好颠倒了.
比时看到的两位数中间多了个0.
如果设小明在时看到的数的十位数字是,那么根据以上信息回答下列问题:(结果均要化简)
(1)时小明看到的数可表示为 ;
(2)时小明看到的数可表示为 ,间摩托车行驶的路程是 ;
(3)时小明看到的数可表示为 ,问摩托车行驶的路程是 ;
(4)利用一元一次方程求出小明在时看到的里程碑上的数是多少?
【答案】(1);
(2),;
(3),;
(4)16.
【分析】(1)由小明在看到的两位数的两个数字之和为7及十位数字为,可得出小明在时看到的数的个位数字是,利用小明在时看到的数十位数字个位数字,即可用含的代数式表示出小明在时看到的数;
(2)利用小明在时看到的数个位数字十位数字,可用含的代数式表示出小明在时看到的数,再利用间摩托车行驶的路程小明在时看到的数小明在时看到的数,即可用含的代数式表示出间摩托车行驶的路程;
(3)利用小明在时看到的数十位数字个位数字,可用含的代数式表示出小明在时看到的数,再利用间摩托车行驶的路程小明在时看到的数小明在时看到的数,即可用含的代数式表示出间摩托车行驶的路程;
(4)根据摩托车的行驶速度不变,可得出关于的一元一次方程,解之即可求出的值,再将其代入中即可求出结论.
【解答】解:(1)小明在看到的数是一个两位数字,它的两个数字之和为7,小明在时看到的数的十位数字是,
小明在时看到的数的个位数字是,
小明在时看到的数是.
故答案为:;
(2)根据题意得:时小明看到的数是,
间摩托车行驶的路程是.
故答案为:,;
(3)根据题意得:时小明看到的数是,
问摩托车行驶的路程是.
故答案为:,;
(4)根据题意得:,
解得:,
.
答:小明在时看到的里程碑上的数是16.
28.如图在数轴上点表示数,点表示数,、满足.
(1)点表示的数为 ;点表示的数为 ;
(2)若在原点处放一挡板,一小球甲从点处以1个单位秒的速度向左运动;同时另一小球乙从点处以3个单位秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为(秒,
①当时,甲小球到原点的距离 ;乙小球到原点的距离 ;
当时,甲小球到原点的距离 ;乙小球到原点的距离 ;
②试探究:甲,乙两小球到原点的距离可能相等吗?若不能,请说明理由若能,请求出甲,乙两小球到原点的距离相等时的值.
③若当甲和乙开始运动时,挡板也从原点以1个单位秒的速度向右运动,直接写出甲,乙两小球到挡板的距离相等时的值.
【答案】(1),4;
(2)①3,1,4,2;
②当秒或秒时,甲乙两小球到原点的距离相等;
③.
【分析】(1)利用绝对值的非负性即可确定出,即可;
(2)①根据运动确定出运动的单位数,即可得出结论;
②根据,(Ⅱ),根据甲、乙两小球到原点的距离相等列出关于的方程,解方程即可;
③分当都向左运动时时,当反弹时,表示出甲、乙两小球之间的距离即可.
【解答】解:(1),
,,
点表示的数为,点表示的数为4,
故答案为:,4;
(2)①当时,
一小球甲从点处以1个单位秒的速度向左运动,
甲小球1秒钟向左运动1个单位,此时,甲小球到原点的距离,
一小球乙从点处以3个单位秒的速度也向左运动,
乙小球1秒钟向左运动3个单位,此时,乙小球到原点的距离,
当时,
一小球甲从点处以1个单位秒的速度向左运动,
甲小球1秒钟向左运动2个单位,此时,甲小球到原点的距离,
一小球乙从点处以3个单位秒的速度也向左运动,
乙小球1秒钟向左运动6个单位,此时,乙小球到原点的距离,
故答案为:3,1,4,2;
②当时,得,
解得;
当时,得,
解得;
故当秒或秒时,甲乙两小球到原点的距离相等;
(3)碰到挡板需要(秒,碰到挡板需要(秒,
时,甲,乙两小球到挡板的距离相等,
①都向左运动时,则,即,
解得,
②反弹时,则,即,
当时,不符合题意舍去,
值为时,甲,乙两小球到挡板的距离相等.
29.如图,已知线段,点为线段上一点,且.动点以的速度,从点出发,沿方向运动,运动到点停止;点出发后,点以的速度,从点出发,沿方向运动,运动到点时,停留,按原速沿方向运动到点停止.设的运动时间为.
(1) 8 , ;
(2)当从向运动时,若,求的值.
(3)当时,直接写出的值.
【答案】(1)8,16;
(2)当从向运动时,若,的值为2;
(3)当时,的值为或或10.
【分析】(1)根据,即可解答;
(2)根据运动时间和运动速度可用含的代数式表示出点、表示的数,再根据列出方程,求解即可;
(3)先求出点追上点的时间,再分三种情况:①当时,即向运动,;②当时,即从向运动,且点在点的左侧,;③当时,即从向运动,且点在点的右侧,;根据不同情况列出方程,再求解即可.
【解答】解:线段,,
,
,
故答案为:8,16;
(2)设的运动时间为,
当从向运动时,点表示的数为,点表示的数为,
则,,
,
,
解得:,
当从向运动时,若,的值为2;
(3)当点追上点时,可得:,
解得:,
①当时,即向运动,,
此时,点表示的数为,点表示的数为,
则,
,
解得:;
②当时,即从向运动,且点在点的左侧,,
此时,点表示的数为,点表示的数为,
则,
,
解得:;
③当时,即从向运动,且点在点的右侧,,
此时,点表示的数为,点表示的数为,
则,
,
解得:;
综上,当时,的值为或或10.
类型7:环形跑道与时钟问题
30.钟表是我们日常生活中常用的计时工具.如图,在圆形钟面上,把一周等分成12个大格,每个大格等分成5个小格,分针和时针均绕中心匀速转动.(本题中的角均指小于的角),
(1)分针每分钟转 6 度,时针每分钟转 度,当时间为时,分针和时针的夹角为 度;
(2)求开始后几分钟分针第一次追上时针;
(3)点为4点钟的位置,平分,平分,从开始计时,分钟后,,求的值.
【答案】(1)6,0.5,75;
(2);
(3)分钟或分钟后,.
【分析】(1)根据圆周是,分别计算时针和分针的转速即可,再根据时时针和分针夹角是2.5个大格计算夹角度数即可;
(2)设分钟后分针第一次追上时针,根据题意列方程求解即可;
(3)根据题意分情况列方程求解即可.
【解答】解:(1)分针每分钟转,时针每分钟转,
时时针和分针夹角是2.5个大格,
时,分针和时针的夹角为,
故答案为:6,0.5,75;
(2)设分钟后分针第一次追上时针,
由题意得,,
解得,
分钟后分针第一次追上时针;
(3)①没追上之前,由题意知,,
解得,
②超过之后,由题意知,,
解得,
分钟或分钟后,.
31.已知环形跑道一圈长为400米,小丽与小杰的速度之比为,如果小丽和小杰在跑道上相距8米处同时反向出发,经过28秒后两人首次相遇,求两人的速度各是多少?
【答案】小丽的速度为6米秒,小杰的速度为8米秒.
【分析】设小丽的速度为米秒,则小杰的速度为米秒,利用路程速度时间,结合经过28秒后两人首次相遇,即可得出关于的一元一次方程,解之即可得出的值,再将其代入和中即可求出结论.
【解答】解:设小丽的速度为米秒,则小杰的速度为米秒,
依题意得:,
解得:,
(米秒),(米秒).
答:小丽的速度为6米秒,小杰的速度为8米秒.
32.周末小明和爸爸在的环形跑道上骑车锻炼,他们在同一地点沿着同一方向同时出发,骑行结束后两人有如下对话:
(1)请根据他们的对话内容,求出小明的骑行速度;
(2)爸爸第一次追上小明后,在第二次相遇前,再经过多少分钟,小明和爸爸在跑道上相距?
【答案】(1)150米分钟;
(2)分钟或分钟.
【分析】(1)设小明的骑行速度为米分钟,则爸爸的骑行速度为米分钟,根据爸爸2分钟才能第一次追上小明,即可得出关于的一元一次方程,解之即可得出结论;
(2)设在第二次相遇前,再经过分钟,小明和爸爸在跑道上相距100米,分爸爸又比小明多骑了100米及爸爸又比小明多骑了米两种情况考虑,利用路程速度时间,即可得出关于的一元一次方程,解之即可得出结论.
【解答】解:(1)设小明的骑行速度为米分钟,则爸爸的骑行速度为米分钟,
依题意得:,
解得:.
答:小明的骑行速度为150米分钟.
(2)设在第二次相遇前,再经过分钟,小明和爸爸在跑道上相距100米,
①爸爸又比小明多骑了100米,
依题意得:,
解得:;
②爸爸又比小明多骑了米,
依题意得:,
解得:.
答:在第二次相遇前,再经过分钟或分钟,小明和爸爸在跑道上相距100米.
33.周末,小明和爸爸在400米的环形跑道上骑车锻炼,他们在同一地点沿着同一方向同时出发,骑行结束后两人有如下对话:
请根据他们的对话内容,求小明和爸爸的骑行速度.
【答案】小明的骑行速度为200米分,爸爸的骑行速度为400米分.
【分析】设小明的骑行速度为米分,则爸爸的骑行速度为米分,根据距离速度差时间即可得出关于的一元一次方程,解之即可得出结论.
【解答】解:设小明的骑行速度为米分,则爸爸的骑行速度为米分,
根据题意得:,
解得:,
.
答:小明的骑行速度为200米分,爸爸的骑行速度为400米分.
34.正方形的轨道上有两个点甲与乙,开始时甲在处,乙在处,它们沿着正方形轨道顺时针同时出发,甲的速度为每秒,乙的速度为每秒.
已知正方形轨道的边长为,求乙在第5次追上甲时在哪条线段上?
【答案】线段上.
【分析】设乙走秒第一次追上甲,设乙再走秒第二次追上甲.根据题意分别列一元一次方程,然后寻找规律解题.
【解答】解:设乙走秒第一次追上甲.
根据题意,得.
解得.
乙走1秒第一次追上甲,则乙在第1次追上甲时的位置是上;
设乙再走秒第二次追上甲.
根据题意,得,
解得.
乙再走2秒第二次追上甲,则乙在第2次追上甲时的位置是上;
同理:乙再走2秒第三次次追上甲,则乙在第3次追上甲时的位置是上;
乙再走2秒第四次追上甲,则乙在第4次追上甲时的位置是上;
乙在第5次追上甲时的位置又回到线段上.
类型8:方案选择类问题
35.永辉超市为春节促销,特推出了两种购物方案.
方案一:非会员购物所有商品价格可获九折优惠;
方案二:如交纳400元会费成为该超市会员,则所有商品价格可获八五折优惠.
(1)以(元表示商品价格,分别用含有的式子表示出两种购物方案中支出金额;
(2)若某人计划在超市购买价格为5800元的电视机一台,请分析选择哪种方案更省钱?
(3)哪种情况下,两种方案的支出金额相同?
【分析】(1)根据题意列出代数式即可;
(2)根据两种方案算出支出金额即可;
(3)根据题意列出方程即可求出的值.
【解答】解:(1)方案一的支出金额为:,
方案二的支出金额为:;
(2)当时,
,
,
答:方案一更为省钱;
(3)当,
解得:,
答:当时,两种方案的支出金额相同
36.某校七年级准备观看电影《长津湖》,由各班班长负责买票,每班人数都多于40人,票价每张30元,一班班长问售票员买团体票是否可以优惠,售票员说:40人以上的团体票有两种优惠方案可选择:方案一:全体人员可打8折;方案二:若打9折,有5人可以免票.
(1)若二班有42名学生,则他该选择哪个方案?
(2)一班班长思考一会儿说,我们班无论选择哪种方案要付的钱是一样的,你知道一班有多少人吗?
【分析】(1)分别计算出方案一和方案二的花费,然后比较大小即可解答本题;
(2)设一班有人,根据已知得出两种方案费用一样,进而列出方程求解即可.
【解答】解:(1)由题意可得,
方案一的花费为:(元,
方案二的花费为:(元,
,
若二班有42名学生,则他该选选择方案二;
(2)设一班有人,根据题意得,
,
解得.
答:一班有45人.
37.下表是中国电信两种” 套餐”计费方式.(月基本费固定收,主叫不超主叫时间,流量不超上网流量不收费,主叫超时和上网超流量部分加收超时费和超流量费)
月基本费元 主叫通话分钟 上网流量 接听 主叫超时部分(元分钟) 超出流量部分(元
方式一 49 200 500 免费 0.20 0.15
方式二 69 250 600 免费 0.15 0.1
(1)若某月小萱主叫通话时间为220分钟,上网流量为,则她按方式一计费需 98 元,按方式二计费需 元,所以她应该选择方式 ;
(2)若小萱某月主叫通话时间为100分钟,是否存在某上网流量,按方式一和方式二的计费相等?若存在,请求出的值:若不存在,请说明理由.
(3)若小萱每月主叫通话时间在100分钟以内,要选择更低的计费方式,请你帮助她做出选择,直接写出结果即可.
【答案】(1)98,89,二;
(2)存在,理由见解析;
(3)当上网流量未超过时,应选择方式一,当上网流量超过时,应选择方式二.
【分析】(1)根据表格中的数据分别计算出两种计费方式所需费用,再进行比较即可解答;
(2)分,,三种情况,分别列出方程,解出即可求解;
(3)分析(2)中结果,即可得出结论.
【解答】解:(1)方式一:
(元,
方式二:
(元,
,
她应该选择方式二;
故答案为:98,89,二;
(2)存在,理由如下:
①当时,
方式一计费需49元,方式而计费需69元,
,
不符合题意;
②当时,
根据题意得:,
解得:(舍去);
③当时,
根据题意得:,
解得:;
综上,当上网流量为,按方式一和方式二的计费相等.
(3)由(2)可知,当上网流量未超过时,应选择方式一,当上网流量超过时,应选择方式二.
38.某校体育社团由于报名人数激增,决定从某体育用品店购买若干足球和篮球,用于日常训练.已知每个篮球的价格比每个足球的价格多30元,用900元购买足球的数量是用720元购买篮球数量的2倍.
(1)求篮球和足球的单价各是多少?
(2)根据学生报名情况,社团需一次性购买篮球和足球共80个,且要求购买足球数量不超过篮球数量的请问社团购买多少个篮球时,能使购买费用最少?
【答案】(1)篮球的单价是80元,足球的单价是50元;
(2)社团购买60个篮球时费用最少,最少费用为5800元.
【分析】(1)设足球的单价是元,则篮球的单价是元,根据用900元购买足球的数量是用720元购买篮球数量的2倍列出方程,解方程即可;
(2)设学校可以购买个篮球,则可以购买个足球,购买费用为元,根据总费用购买篮球和足球费用的和列出函数解析式,再根据购买足球数量不超过篮球数量的,求出的取值范围,再根据函数的性质求最值.
【解答】解:(1)设足球的单价是元,则篮球的单价是元,
根据题意,得,
解得,
经检验,是原方程的解,且符合题意,
.
答:篮球的单价是80元,足球的单价是50元;
(2)设学校购买个篮球,则购买足球个,购买费用为元,
则,
购买足球数量不超过篮球数量的,
,
解得,
,
当时,有最小值,最小值为5800元,
此时,
答:社团购买60个篮球时费用最少,最少费用为5800元.
39.2021年“双十一”期间,很多国货品牌受到人们的青睐,销量大幅增长.某平台的体育用品旗舰店实行优惠销售,规定如下:对原价160元件的某款运动速干衣和20元双的某款运动棉袜开展促销活动,活动期间向客户提供两种优惠方案.
方案:买一件运动速干衣送一双运动棉袜;
方案:运动速干衣和运动棉袜均按9折付款.
某户外俱乐部准备购买运动速干衣30件,运动棉袜双.
(1)若该户外俱乐部按方案购买,需付款 元(用含的式子表示);若该户外俱乐部按方案购买,需付款 元(用含的式子表示);
(2)若,通过计算说明此时按哪种方案购买较为合算;
(3)当购买运动棉袜多少双时两种方案付款相同.
【答案】(1),;
(2)按方案购买较为合算;理由见解答部分;
(3)当购买运动棉袜60双时,两种方案付款相同.
【分析】(1)根据两种不同的优惠方案列出代数式即可;
(2)将分别代入(1)所列代数式计算比较即可;
(3)根据“两种方案付款相同”列出方程并解答.
【解答】解:(1)按方案购买,需付款:,
即需要付款元;
按方案购买,需付款:,
即需要付款元.
故答案为:,;
(2)当时,
方案(元.
方案(元.
因为,所以按方案购买较为合算;
(3)根据题意,得.
解得.
答:当购买运动棉袜60双时,两种方案付款相同.
类型9:储蓄、利息问题
40.小希准备在6年后考上大学时,用15000元给父母买一份礼物表示感谢,决定现在把零花钱存入银行.下面有两种储蓄方案:
①直接存一个6年期.年期年利率为
②先存一个3年期,3年后本金与利息的和再自动转存一个3年期.年期年利率为
你认为按哪种储蓄方案开始存入的本金比较少?请通过计算说明理由.
【分析】设储蓄方案①所需本金元,储蓄方案②所需本金元,根据本息和本金利率期数),即可得出关于的一元一次方程,解之即可得出的值,比较后即可得出结论.
【解答】解:设储蓄方案①所需本金元,储蓄方案②所需本金元.
依题意,得:,,
解得:,,
,
按照储蓄方案①开始存入的本金比较少.
41.小明的爸爸开了一家运动品商店,近期商店购进一批运动服,按进价提高后打八折出售,这时每套运动服的售价为140元.
(1)求每套运动服的进价?
(2)运动服卖出一半后,正好赶上双十一促销,商店决定将剩下的运动服每3套400元的价格出售,很快销售一空,后一半促销获利5000元,求小明的爸爸共购进多少套运动服?
(3)最后,小明的爸爸决定将整批运动服的利润当做小明的教育基金存入银行,已知该银行3年期的固定储蓄年利率为,求3年后取出的本息和为多少元?
【分析】(1)设每套运动服的进价为元,根据打折后每套运动服的售价为140元,即可得出关于的一元一次方程,解之即可得出结论;
(2)设小明的爸爸共购进套运动服,根据后一半促销获利5000元,即可得出关于的一元一次方程,解之即可得出结论;
(3)根据本息和本金利润率年限),即可求出结论.
【解答】解:(1)设每套运动服的进价为元,
依题意,得:,
解得:.
答:每套运动服的进价为125元.
(2)设小明的爸爸共购进套运动服,
依题意,得:,
解得:.
答:小明的爸爸共购进1200套运动服.
(3)(元.
答:3年后取出的本息和为15134元.
42.妈妈为小华存了一个3年期的教育储蓄(设3年期的年利率为,3年后能取10350元,妈妈开始存入了多少元?
【分析】设妈妈开始存入了元,根据本金本金利率时间列出方程,解方程即可.
【解答】解:设妈妈开始存入了元,根据题意得,
,
解得,.
答:妈妈开始存入了9000元.
43.小明的爸爸三年前为小明存了一份3000元的教育储蓄.今年到期时取出,得本利和为3243元.请你帮小明算一算这种储蓄的年利率.
【分析】不用交利息税的本利和计算方法为:本利和本金本金年利率时间,利用本利和为3243元作为相等关系列方程求解即可.
【解答】解:设这种储蓄的年利率为,
则:,
解之得:.
即.
答:这种储蓄的年利率为.
44.李明存入银行一笔钱,整存整取3年,年利率,到期后共取出5375元,求李明存入了多少钱?
【答案】李明存入5000元.
【分析】设李明存入元,根据本息和本金年份年利率本金,即可得出关于的一元一次方程,解之即可得出结论.
【解答】解:设李明存入元,则
,
解得,
答:李明存入5000元.
一 类型10:产品配套问题
45.用白铁皮做罐头盒,每张铁皮可制盒身25个,或制盒底40个,一个盒身与两个盒底配成一套.现在有36张白铁皮,用多少张制盒身,多少张制盒底,可使盒身与盒底正好配套?
【分析】可设用张制盒身,则张制盒底,可使盒身与盒底正好配套,根据等量关系:一个盒身与两个盒底配成一套.列出方程求解即可.
【解答】解:设用张制盒身,则张制盒底,
根据题意,得到方程:,
解得:,
.
答:用16张制盒身,20张制盒底,可使盒身与盒底正好配套.
46.列方程,解应用题:
新型冠状肺炎疫情正在全球蔓延肆虐,口罩成了人们生活中必不可少的物品,某口罩厂有40名工人,每人每天可以生产1000个口罩面或1200根耳绳.一个口罩面需要配两根耳绳,为使每天生产的口罩面与耳绳刚好配套,应安排多少名工人生产口罩面?
【分析】根据人每天可以生产1000个口罩面或1200根耳绳,一个口罩面需要配两根耳绳,可以列出相应的方程,然后解方程,即可解答本题.
【解答】解:设应安排名工人生产口罩面,则安排名工人生产耳绳,
,
解得,
答:应安排15名工人生产口罩面.
47.疫情防控期间,口罩成为人们生活中必不可少的物品.某口罩厂有87名工人,每人每天可以生产900个口罩面或1100个口罩耳绳,一个口罩面需要配两个耳绳.
(1)为使每天生产的口罩面和口罩耳绳刚好配套,应安排多少名工人生产口罩面?
(2)若该工厂某天生产的口罩面与口罩耳绳刚好配套,设一个成品口罩成本价是元,售价是元,请用含、的式子表示该口罩厂该天生产口罩的利润.
【答案】(1)应安排33名工人生产口罩面;
(2)该口罩厂该天生产口罩的利润为元.
【分析】(1)设安排名工人生产口罩面,则有名工人生产口罩耳绳,根据每天生产的口罩面和口罩耳绳刚好配套列出方程,解出方程即可得到答案;
(2)由(1)可算出该天生产成品口罩的数量,再根据利润(单个售价单个成本)数量列出代数式即可得到答案.
【解答】解:(1)设安排名工人生产口罩面,则有名工人生产口罩耳绳,
根据题意得:,
解得:,
应安排33名工人生产口罩面;
(2)由(1)可得,该天生产成品口罩的数量为:(个,
则该口罩厂该天生产口罩的利润为:元.
48.用相同规格的正方形硬纸板做成如图1的直三棱柱盒子,每个盒子由3个相同的长方形做侧面和2个相同的正三角形做底面组成,硬纸板按如图2的两种方法裁剪(裁剪后边角料不再利用).
方法:剪出6个侧面;方法:剪出4个侧面和5个底面.
现有19张这种规格的正方形硬纸板,裁剪时张用方法,其余用方法.
(1)用含的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,则能做多少个盒子?
【答案】(1)裁剪出个侧面,个底面;
(2)能做30个盒子.
【分析】(1)由正方形硬纸板的张数及按方法裁剪的张数,可得出裁剪时张用方法,结合两种方法裁剪出的侧面及底面的数量,即可用含的代数式表示出裁剪出的侧面和底面的个数;
(2)由每个盒子由3个侧面和2个底面组成,结合裁剪出的侧面和底面恰好全部用完,可得出关于的一元一次方程,解之可得出的值,再将其代入中,即可求出结论.
【解答】解:(1)共有19张这种规格的正方形硬纸板,且裁剪时张用方法,
裁剪时张用方法,
裁剪出个侧面,个底面.
裁剪出个侧面,个底面;
(2)根据题意得:,
解得:,
.
答:能做30个盒子.
49.在手工制作课上,老师组织七年级(2)班的学生用硬纸制作圆柱形茶叶筒.七年级(2)班共有学生44人,其中男生人数比女生人数少2人,并且每名学生每小时剪筒身50个或剪筒底120个.
(1)七年级(2)班有男生、女生各多少人?
(2)要求一个筒身配两个筒底,为了使每小时剪出的筒身与筒底刚好配套,应该分配多少名学生剪筒身,多少名学生剪筒底?
【分析】(1)设七年级(2)班有女生人,则男生人,根据全班共有44人建立方程求出其解即可;
(2)设分配人生产筒身,人生产筒底,由筒身与筒底的数量关系建立方程求出其解即可.
【解答】解:(1)设七年级(2)班有女生人,则男生人,由题意,得
,
解得:,
男生有:人.
答:七年级(2)班有女生23人,则男生21人;
(2)设分配人生产筒身,人生产筒底,由题意,得
,
解得:.
生产筒底的有20人.
答:分配24人生产筒身,20人生产筒底.
思维导图:
类型1:和、差、倍、分型应用题
1.我们定义:如果线段上的一个点将这条线段分成长度分别是,的两部分,并且满足,那么这个点叫做这条线段的“三高四新点”.
(1)如图1,点是线段的“三高四新点”, 且,则 ;
(2)若点也是(1)中线段的“三高四新点”(不同于点),求与的数量关系;
(3)如图2,点是数轴原点,点对应的数是3,点对应的数是12,在点处有一挡板.小球从点出发以每秒1个单位长度的速度向左匀速运动,小球从点同时出发,以每秒3个单位长度的速度向右匀速运动,碰到挡板后立即以每秒3个单位长度的速度向左运动.追上时,两小球同时停止运动.设运动时间为秒,当、、三点中某一点为其余两点所构成线段的“三高四新点”时,请求出的值.
2.学校开展大课间活动,五(1)班有的学生参加了跳绳活动,的同学参加乒乓球活动,剩下的15人全部踢足球,五(1)班共有多少人?
3.如表是两种“优惠套餐”计费方式.(月费固定收,主叫不超时,流量不超量不再收费,主叫超时和上网超流量部分加收超时费和超流量费)
月费(元 主叫(分钟) 流量 接听 超时(元钟) 超流量(元
方式一 49 200 50 免费 0.20 3
方式二 69 250 65 免费 0.15 2
(1)若某月小郭主叫通话时间为320分钟,上网流量为,则她按方式一计费需 元,按方式二计费需 元;若她按方式二计费需119元,主叫通话时间为234分钟,则上网流量为 ;
(2)若上网流量为,是否存在某主叫通话时间(分钟),按方式一和方式二的计费相等?若存在,请求出的值;若不存在,请说明理由.
4.如图,已知在数轴上有、两点,点表示的数是,点表示的数是9.点在数轴上从点出发,以每秒2个单位的速度沿数轴正方向运动,同时,点在数轴上从点出发,以每秒3个单位的速度沿数轴负方向运动,当点到达点时,两点同时停止运动.设运动时间为秒.
(1)求的距离;
(2)当时,点、点分别表示什么数?
(3)当为何值时,、两点相遇?
类型2:等积变形类应用题
5.小林用一根质地均匀的木杆和一些等重的小物体做实验.如图:他在木杆的正中间处栓绳,将木杆吊起来,吊绳处为木杆的支点,记为.然后在木杆的左边挂个重物,在木杆的右边挂个重物,且.并通过移动左右两边的重物直至木杆平衡.记平衡时木杆左边挂重物的位置为,木杆右边挂重物的位置为、多次实验后、小林发现了规律:,即木杆平衡时,左边挂重物的个数支点到木杆左边挂重物处的距离右边挂重物的个数支点到木杆右边挂重物处的距离.
(1)填空: (用含有和的式子表示);
(2)设木杆上中点的位置为.
①若,,,求;
②问:是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
6.有一位工人师傅将底面直径为,高为的实心圆柱,锻造成底面直径为的实心圆柱,求锻造后圆柱的高是多少?
7.将一个底面半径为、高为的“瘦长”圆柱体钢材锻压成底面直径为的“矮胖”圆柱体零件毛坯问:毛坯的高是多少?(列方程解答)
8.如图,小明将一个正方形纸片剪去一个宽为5厘米的长条后,再从剩下的长方形纸片上剪去一个宽6厘米的长条,如果两次剪下的长条面积正好相等,那么每一个长条的面积为多少?
9.一个长,宽,高为的长方体容器中装满了水.小明先把容器中的水倒满2个底面半径为,高为的圆柱体杯子,再把剩下的水全部倒入瓶子甲中.当瓶子甲正放时如图1,瓶内溶液的高度为;瓶子甲倒放时如图2,空余部分的高度为.求瓶子甲的容积.取3,容器的厚度不计)
类型3:工程类应用题
10.为打造“安全、环保、生态”的某河流公园,某市设立若干河流排污治理点(每处需安装相同长度的排污治理管道),一天甲队3名工人去完成5个治理点管道铺设,但还有60米管道未来得及完成,乙队4名工人完成5个治理点后,仍多铺设了40米管道,每名甲队工人比乙队工人每天多铺设20米管道.
(1)求每个排污治理点需铺设的管道长度;
(2)已知每位甲队工人每天需支付费用500元,每名乙队工人每天需支付400元,该市共设立50个排污治理点,另有5880米的同样的污水排放管道也需要安装.现有甲队3名工人,乙队4名工人来安装管道,方案一:全部由甲队安装;方案二:全部由乙队安装;(不到一天按一天算).若要使总费用最少,应选择哪种方案?请通过计算说明.
11.我区某中学举办一年一届的科技文化艺术节活动,需搭建一个舞台,请来两名工人.已知甲单独完成需4小时,乙单独完成需6小时.现由乙提前做1小时,剩下的工作由甲、乙两人合做,问再合做几小时可以完成这项工作?
12.某公司需要加工一批零件,甲每天可以加工16个零件,乙每天可以加工24个零件,甲单独加工这批零件比乙单独加工这批零件多用20天,甲每天的人工费为80元,乙每天的人工费为120元.
(1)问这批零件共有多少个?
(2)在加工零件过程中,公司要派一名质量监督员,并且每天支付他15元补助费,现有三种加工方案:①由甲单独加工这批零件;②由乙单独加工这批零件;③甲、乙合作同时加工这批零件,你认为哪种方案最省钱,为什么?
13.一项工程,甲队单独完成需要40天,乙队单独完成需要50天,现甲队单独做4天后两队合作.
(1)求甲、乙两队合作多少天才能完成该工程.
(2)在(1)的条件下,甲队每天的施工费为3000元,乙队每天的施工费为3500元,求完成此项工程需付给甲乙两队共多少元.
14.甲、乙两队修一座桥,如果由甲队单独完成,需要15天;如果由乙队单独完成,需要30天.现在由甲队单独做了3天后,承办方接到通知,需要加快修桥进度,后续工程由甲、乙两队共同完成,则甲、乙两队后续需要合作多少天才能修完这座桥?
类型4:销售类应用题
15.列方程解决问题:
在“双11”促销活动中,某商场一运动品牌店实施如下调价方案:先把每件商品按原价提价后标价,又以6折销售,一套运动服经过上述调价后售价为270元.
(1)这套运动服的原价为多少元?
(2)在促销活动期间,乐乐妈妈到该品牌店购买了3套该运动服,所花的钱比调价方案前优惠了多少元?
16.小明用的练习本可以到甲、乙两家商店购买,已知两商店的标价都是每本2元,甲商店的优惠条件是购买10本以上,从第11本开始按标价的出售;乙商店的优惠条件是,从第一本起按标价的出售.若小明要购买本练习本.
(1)则当小明到甲商店购买时,需付款 元;当到乙商店购买时,需付款 元;
(2)买多少本练习本时,两家商店花费相同?
(3)小明准备买50本练习本,为了节约开支,选择哪家更划算?
17.忠县重百电商通过互联网销售某品牌电话手表,第一周的总销售额为5520元,第二周的总销售额为6840元,第二周比第一周多售出22块电话手表.
(1)求每块电话手表的售价;
(2)该公司在第三周将每块电话手表的售价降低了,并预计第三周能售出158块电话手表,由于恰逢开学周,不少家庭为子女购买电话手表,该款手表在第三周的销量比预计还多了.如果每块电话手表成本为42元,该公司第三周销售手表的总利润为3318元,求的值.
18.平价商场恰好用3800元购进甲,乙两种商品共50件,若甲种商品每件进价70元,乙种商品每件进价80元,且统一标价120元出售.
(1)求购进甲、乙两种商品各多少件?
(2)该商场售出这批商品的一部分后,恰逢“元旦”对剩余商品进行促销,以标价的8折售完所有剩余商品,共获利1480元,且促销商品中乙的件数是甲件数的1.5倍,求促销商品中甲商品有多少件?
19.“广交会”是中国历史最长的综合性国际贸易盛会.在“广交会”中,某到会采购商计划从厂家购进甲、乙两种商品.已知甲种商品的每件进价比乙种商品的每件进价少20元.若购进甲种商品5件,乙种商品3件,共需要700元.
(1)求甲、乙两种商品的每件进价分别是多少元?
(2)该采购商从厂家购进了甲种商品3万件、乙种商品2万件.在销售时,甲种商品的每件售价为110元,要使得这5万件商品所获利润率为,求每件乙种商品的售价是多少元?
类型5:比赛类应用题
20.为了迎接世界杯足球赛的到来,足球协会举办了一次足球赛,其中得分规则及奖励方案如表:
胜一场 平一场 负一场
积分 3 1 0
人均奖金 1500元 700元 0
当比赛进行到每队比赛完12场时,队共积分20分,并且没有负一场.
(1)试判断队胜、平各几场?
(2)每赛一场,队每名队员均得出场费500元,那么比赛完12场后,队每名队员所得奖金与出场费累计为多少元?
21.在2022年女足亚洲杯决赛中,中国女足以逆转韩国女足,时隔16年再夺亚洲杯冠军!某学校掀起一股足球热,举行了班级联赛,九(1)班开局11场保持不败,共积23分,按照比赛规则,胜一场积3分,平一场积1分,负一场积0分,求该班获胜的场数.
22.篮球运动是最流行的运动之一,深受青少年喜爱.某市举办春季校园篮球赛,共有八支队伍参赛,其中三支队伍的积分表如下.请根据表格信息解答下列问题:
队名 比赛场次 胜场 负场 积分
前进 14 10 4 24
光明 14 9 5 23
远方 14 0 14 14
(1)请回答:胜一场得 分,负一场得 分;
(2)若某队胜场总积分是负场总积分的2倍,求该队的胜场数;
(3)若某队的负场总积分是胜场总积分的正整数倍,求该队的胜场数.
23.在一次知识竞赛中,甲、乙两班各有50位同学参加比赛,每位同学都需要完成三道题的答题,竞赛规则为:“答对一题得10分,不答或者答错扣10分”.
(1)请直接写出每位同学所有可能的得分情况;
(2)甲班的答题情况为:有2位同学全部答错,全对的人数是答对1题人数的3倍少6人,答对两题的人数是答对1题人数的2倍;乙班的答题情况为:没有同学全部答错,答对一题人数的3倍和答对2题的人数之和等于全部答对的人数.
①求甲班全部答对的人数;
②请判断甲乙两班哪个班的得分更高,并说明理由.
24.2022世界杯于11月21日在卡塔尔召开.在小组赛阶段,32支球队根据自身实力所处的不同档次,以及所属大洲的情况进行抽签选择,每个小组4支球队.在小组内部的球队会和其他三支队伍都进行比赛,以下是世界杯小组赛组的积分表.
小组 代表队 场次(场 胜(场 平(场 负(场 积分(分
组 荷兰 3 2 1 0 7
塞内加尔 3 2 0 1 6
厄瓜多尔 3 1 1 1 4
卡塔尔 3 0 0 3 0
(说明:积分胜场积分平场积分负场积分)
(1)求小组赛中胜一场、平一场、负一场各积多少分?
(2)小组赛结束时,阿根廷队没有平场,并且小组赛积分6分,成功晋级,求阿根廷队胜、负各多少场?
(3)在本次小组赛中,能否出现一支球队保持不败的战绩,且胜场总积分恰好等于它的平场总积分?
类型6:行程类应用题
25.甲、乙两队相约沿相同的路线徒步,徒步的路程为,甲队步行速度为,乙队步行速度为,甲队出发后,乙队才出发.
(1)问乙队需要多长时间可以追上甲队;
(2)从甲队出发开始到乙队完成徒步路程止,甲队出发多长时间,两队间隔的路程为.
26.已知数轴上两点、对应的数分别为、4,点为数轴上一动点.
(1)若点到点、点的距离相等,求点对应的数;
(2)数轴上是否存在点,使点到点、点的距离之和为18?若存在,请求出点所表示的数;若不存在,说明理由;
(3)现在点以3个单位长度秒的速度向右运动,点以1个单位长度秒的速度向左运动,点以2个单位长度秒的速度从点向右运动.点、、三点同时运动,当点与点之间的距离为4个单位长度时,求点所对应的数是多少?
27.小明爸爸骑着摩托车带着小明在公路上匀速行驶,如表是小明每隔1小时看到的里程情况,你能确定小明在时看到的里程碑上的数吗?
时间 里程情况
是一个两位数字,它的两个数字之和为7.
十位与个位数字与时所看到的正好颠倒了.
比时看到的两位数中间多了个0.
如果设小明在时看到的数的十位数字是,那么根据以上信息回答下列问题:(结果均要化简)
(1)时小明看到的数可表示为 ;
(2)时小明看到的数可表示为 ,间摩托车行驶的路程是 ;
(3)时小明看到的数可表示为 ,问摩托车行驶的路程是 ;
(4)利用一元一次方程求出小明在时看到的里程碑上的数是多少?
28.如图在数轴上点表示数,点表示数,、满足.
(1)点表示的数为 ;点表示的数为 ;
(2)若在原点处放一挡板,一小球甲从点处以1个单位秒的速度向左运动;同时另一小球乙从点处以3个单位秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为(秒,
①当时,甲小球到原点的距离 ;乙小球到原点的距离 ;
当时,甲小球到原点的距离 ;乙小球到原点的距离 ;
②试探究:甲,乙两小球到原点的距离可能相等吗?若不能,请说明理由若能,请求出甲,乙两小球到原点的距离相等时的值.
③若当甲和乙开始运动时,挡板也从原点以1个单位秒的速度向右运动,直接写出甲,乙两小球到挡板的距离相等时的值.
29.如图,已知线段,点为线段上一点,且.动点以的速度,从点出发,沿方向运动,运动到点停止;点出发后,点以的速度,从点出发,沿方向运动,运动到点时,停留,按原速沿方向运动到点停止.设的运动时间为.
(1) , ;
(2)当从向运动时,若,求的值.
(3)当时,直接写出的值.
类型7:环形跑道与时钟问题
30.钟表是我们日常生活中常用的计时工具.如图,在圆形钟面上,把一周等分成12个大格,每个大格等分成5个小格,分针和时针均绕中心匀速转动.(本题中的角均指小于的角),
(1)分针每分钟转 度,时针每分钟转 度,当时间为时,分针和时针的夹角为 度;
(2)求开始后几分钟分针第一次追上时针;
(3)点为4点钟的位置,平分,平分,从开始计时,分钟后,,求的值.
31.已知环形跑道一圈长为400米,小丽与小杰的速度之比为,如果小丽和小杰在跑道上相距8米处同时反向出发,经过28秒后两人首次相遇,求两人的速度各是多少?
32.周末小明和爸爸在的环形跑道上骑车锻炼,他们在同一地点沿着同一方向同时出发,骑行结束后两人有如下对话:
(1)请根据他们的对话内容,求出小明的骑行速度;
(2)爸爸第一次追上小明后,在第二次相遇前,再经过多少分钟,小明和爸爸在跑道上相距?
33.周末,小明和爸爸在400米的环形跑道上骑车锻炼,他们在同一地点沿着同一方向同时出发,骑行结束后两人有如下对话:
请根据他们的对话内容,求小明和爸爸的骑行速度.
34.正方形的轨道上有两个点甲与乙,开始时甲在处,乙在处,它们沿着正方形轨道顺时针同时出发,甲的速度为每秒,乙的速度为每秒.
已知正方形轨道的边长为,求乙在第5次追上甲时在哪条线段上?
类型8:方案选择类问题
35.永辉超市为春节促销,特推出了两种购物方案.
方案一:非会员购物所有商品价格可获九折优惠;
方案二:如交纳400元会费成为该超市会员,则所有商品价格可获八五折优惠.
(1)以(元表示商品价格,分别用含有的式子表示出两种购物方案中支出金额;
(2)若某人计划在超市购买价格为5800元的电视机一台,请分析选择哪种方案更省钱?
(3)哪种情况下,两种方案的支出金额相同?
36.某校七年级准备观看电影《长津湖》,由各班班长负责买票,每班人数都多于40人,票价每张30元,一班班长问售票员买团体票是否可以优惠,售票员说:40人以上的团体票有两种优惠方案可选择:方案一:全体人员可打8折;方案二:若打9折,有5人可以免票.
(1)若二班有42名学生,则他该选择哪个方案?
(2)一班班长思考一会儿说,我们班无论选择哪种方案要付的钱是一样的,你知道一班有多少人吗?
37.下表是中国电信两种” 套餐”计费方式.(月基本费固定收,主叫不超主叫时间,流量不超上网流量不收费,主叫超时和上网超流量部分加收超时费和超流量费)
月基本费元 主叫通话分钟 上网流量 接听 主叫超时部分(元分钟) 超出流量部分(元
方式一 49 200 500 免费 0.20 0.15
方式二 69 250 600 免费 0.15 0.1
(1)若某月小萱主叫通话时间为220分钟,上网流量为,则她按方式一计费需 元,按方式二计费需 元,所以她应该选择方式 ;
(2)若小萱某月主叫通话时间为100分钟,是否存在某上网流量,按方式一和方式二的计费相等?若存在,请求出的值:若不存在,请说明理由.
(3)若小萱每月主叫通话时间在100分钟以内,要选择更低的计费方式,请你帮助她做出选择,直接写出结果即可.
38.某校体育社团由于报名人数激增,决定从某体育用品店购买若干足球和篮球,用于日常训练.已知每个篮球的价格比每个足球的价格多30元,用900元购买足球的数量是用720元购买篮球数量的2倍.
(1)求篮球和足球的单价各是多少?
(2)根据学生报名情况,社团需一次性购买篮球和足球共80个,且要求购买足球数量不超过篮球数量的请问社团购买多少个篮球时,能使购买费用最少?
39.2021年“双十一”期间,很多国货品牌受到人们的青睐,销量大幅增长.某平台的体育用品旗舰店实行优惠销售,规定如下:对原价160元件的某款运动速干衣和20元双的某款运动棉袜开展促销活动,活动期间向客户提供两种优惠方案.
方案:买一件运动速干衣送一双运动棉袜;
方案:运动速干衣和运动棉袜均按9折付款.
某户外俱乐部准备购买运动速干衣30件,运动棉袜双.
(1)若该户外俱乐部按方案购买,需付款 元(用含的式子表示);若该户外俱乐部按方案购买,需付款 元(用含的式子表示);
(2)若,通过计算说明此时按哪种方案购买较为合算;
(3)当购买运动棉袜多少双时两种方案付款相同.
类型9:储蓄、利息问题
40.小希准备在6年后考上大学时,用15000元给父母买一份礼物表示感谢,决定现在把零花钱存入银行.下面有两种储蓄方案:
①直接存一个6年期.年期年利率为
②先存一个3年期,3年后本金与利息的和再自动转存一个3年期.年期年利率为
你认为按哪种储蓄方案开始存入的本金比较少?请通过计算说明理由.
41.小明的爸爸开了一家运动品商店,近期商店购进一批运动服,按进价提高后打八折出售,这时每套运动服的售价为140元.
(1)求每套运动服的进价?
(2)运动服卖出一半后,正好赶上双十一促销,商店决定将剩下的运动服每3套400元的价格出售,很快销售一空,后一半促销获利5000元,求小明的爸爸共购进多少套运动服?
(3)最后,小明的爸爸决定将整批运动服的利润当做小明的教育基金存入银行,已知该银行3年期的固定储蓄年利率为,求3年后取出的本息和为多少元?
42.妈妈为小华存了一个3年期的教育储蓄(设3年期的年利率为,3年后能取10350元,妈妈开始存入了多少元?
43.小明的爸爸三年前为小明存了一份3000元的教育储蓄.今年到期时取出,得本利和为3243元.请你帮小明算一算这种储蓄的年利率.
44.李明存入银行一笔钱,整存整取3年,年利率,到期后共取出5375元,求李明存入了多少钱?
一 类型10:产品配套问题
45.用白铁皮做罐头盒,每张铁皮可制盒身25个,或制盒底40个,一个盒身与两个盒底配成一套.现在有36张白铁皮,用多少张制盒身,多少张制盒底,可使盒身与盒底正好配套?
46.列方程,解应用题:
新型冠状肺炎疫情正在全球蔓延肆虐,口罩成了人们生活中必不可少的物品,某口罩厂有40名工人,每人每天可以生产1000个口罩面或1200根耳绳.一个口罩面需要配两根耳绳,为使每天生产的口罩面与耳绳刚好配套,应安排多少名工人生产口罩面?
47.疫情防控期间,口罩成为人们生活中必不可少的物品.某口罩厂有87名工人,每人每天可以生产900个口罩面或1100个口罩耳绳,一个口罩面需要配两个耳绳.
(1)为使每天生产的口罩面和口罩耳绳刚好配套,应安排多少名工人生产口罩面?
(2)若该工厂某天生产的口罩面与口罩耳绳刚好配套,设一个成品口罩成本价是元,售价是元,请用含、的式子表示该口罩厂该天生产口罩的利润.
48.用相同规格的正方形硬纸板做成如图1的直三棱柱盒子,每个盒子由3个相同的长方形做侧面和2个相同的正三角形做底面组成,硬纸板按如图2的两种方法裁剪(裁剪后边角料不再利用).
方法:剪出6个侧面;方法:剪出4个侧面和5个底面.
现有19张这种规格的正方形硬纸板,裁剪时张用方法,其余用方法.
(1)用含的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,则能做多少个盒子?
49.在手工制作课上,老师组织七年级(2)班的学生用硬纸制作圆柱形茶叶筒.七年级(2)班共有学生44人,其中男生人数比女生人数少2人,并且每名学生每小时剪筒身50个或剪筒底120个.
(1)七年级(2)班有男生、女生各多少人?
(2)要求一个筒身配两个筒底,为了使每小时剪出的筒身与筒底刚好配套,应该分配多少名学生剪筒身,多少名学生剪筒底?
第五章 一元一次方程的应用 【十大类型分类归纳】2023-2024学年北师大版七年级上册
类型1:和、差、倍、分型应用题
1.我们定义:如果线段上的一个点将这条线段分成长度分别是,的两部分,并且满足,那么这个点叫做这条线段的“三高四新点”.
(1)如图1,点是线段的“三高四新点”, 且,则 7 ;
(2)若点也是(1)中线段的“三高四新点”(不同于点),求与的数量关系;
(3)如图2,点是数轴原点,点对应的数是3,点对应的数是12,在点处有一挡板.小球从点出发以每秒1个单位长度的速度向左匀速运动,小球从点同时出发,以每秒3个单位长度的速度向右匀速运动,碰到挡板后立即以每秒3个单位长度的速度向左运动.追上时,两小球同时停止运动.设运动时间为秒,当、、三点中某一点为其余两点所构成线段的“三高四新点”时,请求出的值.
【答案】(1)7;
(2);
(3)当、、三点中某一点为其余两点所构成线段的“三高四新点”时,的值为1,,,,或.
【分析】(1)根据“三高四新点”的定义即可求解;
(2)根据“三高四新点”的定义即可求解;
(3)根据题意,分三种情况:①当时,点向右运动,再分和;②当时,点向左运动,并且在点的右边,再分和;③当时,点向左运动,并且在点的左边,再分和;根据“三高四新点”的定义列出方程,求解即可.
【解答】解:(1)点是线段的“三高四新点”,
,
,
,
;
故答案为:7;
(2)点也是线段的“三高四新点”(不同于点),
,即,
,
,
,
,
;
(3)①当时,点向右运动,点时线段的“三高四新点”,
此时点表示的数为,点表示的数为,
,,
当时,得,解得:,
当时,得,解得:;
②当时,点向左运动,并且在点的右边,
此时点表示的数为,点表示的数为,
,,
当时,得,解得:,
当时,得,解得:;
③当时,点向左运动,并且在点的左边,
此时点表示的数为,点表示的数为,
,,
当时,得,解得:,
当时,得,解得:;
综上,当、、三点中某一点为其余两点所构成线段的“三高四新点”时,的值为1,,,,或.
2.学校开展大课间活动,五(1)班有的学生参加了跳绳活动,的同学参加乒乓球活动,剩下的15人全部踢足球,五(1)班共有多少人?
【答案】36人.
【分析】设五(1)班共有人,根据“跳绳人数乒乓球人数足球人数总人数“列出方程,求解即可.
【解答】解:设五(1)班共有人,
由题意得,
整理,得,
解得.
答:五(1)班共有36人.
3.如表是两种“优惠套餐”计费方式.(月费固定收,主叫不超时,流量不超量不再收费,主叫超时和上网超流量部分加收超时费和超流量费)
月费(元 主叫(分钟) 流量 接听 超时(元钟) 超流量(元
方式一 49 200 50 免费 0.20 3
方式二 69 250 65 免费 0.15 2
(1)若某月小郭主叫通话时间为320分钟,上网流量为,则她按方式一计费需 133 元,按方式二计费需 元;若她按方式二计费需119元,主叫通话时间为234分钟,则上网流量为 ;
(2)若上网流量为,是否存在某主叫通话时间(分钟),按方式一和方式二的计费相等?若存在,请求出的值;若不存在,请说明理由.
【答案】(1)133,89.5;90;
(2)当分钟时,方式一和方式二的计费相等.
【分析】(1)根据主叫通话时间为320分钟,上网流量为,按表格中数据计算即可;根据主叫通话时间为234分钟,设上网流量为,根据题意列出方程,解方程即可;
(2)分,和三种情况,根据方式一和方式二收费相等列出方程,解方程即可.
【解答】解:(1)按方式一:
(元;
按方式二:
(元;
设上网流量为,
根据题意得:,
解得,
上网流量为,
故答案为:133,89.5;90;
(2)存在.
①当时,由题意得:,即,显然不成立;
②当时,由题意得:
,
解得;
③当时,由题意得:
,
解得,不合题意.
综上所述,当分钟时,方式一和方式二的计费相等.
4.如图,已知在数轴上有、两点,点表示的数是,点表示的数是9.点在数轴上从点出发,以每秒2个单位的速度沿数轴正方向运动,同时,点在数轴上从点出发,以每秒3个单位的速度沿数轴负方向运动,当点到达点时,两点同时停止运动.设运动时间为秒.
(1)求的距离;
(2)当时,点、点分别表示什么数?
(3)当为何值时,、两点相遇?
【答案】(1)15个单位长度;
(2)点表示的数是4,点表示的数是6;
(3)3.
【分析】(1)根据两点间距离的定义解得;
(2)当时,利用路程速度时间分别求得、的长度,然后由数轴的性质解答;
(3)根据线段的和差定义计算即可.
【解答】解:(1).
答:的距离为15个单位长度;
(2)当时,
,.
,.
点表示的数是,点表示的数是6;
(3)根据题意,得,
解得.
答:当时,、两点相遇,
类型2:等积变形类应用题
5.小林用一根质地均匀的木杆和一些等重的小物体做实验.如图:他在木杆的正中间处栓绳,将木杆吊起来,吊绳处为木杆的支点,记为.然后在木杆的左边挂个重物,在木杆的右边挂个重物,且.并通过移动左右两边的重物直至木杆平衡.记平衡时木杆左边挂重物的位置为,木杆右边挂重物的位置为、多次实验后、小林发现了规律:,即木杆平衡时,左边挂重物的个数支点到木杆左边挂重物处的距离右边挂重物的个数支点到木杆右边挂重物处的距离.
(1)填空: (用含有和的式子表示);
(2)设木杆上中点的位置为.
①若,,,求;
②问:是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
【答案】(1);
(2);
(3)是定值,定值为.
【分析】(1)根据小林发现的规律:即可解答;
(2)①设,则,根据,列出方程求得,,根据线段中点性质的,则;
(3)分和两种情况,先分别表示出的长,再表示出,以此即可求解.
【解答】(1)由题意可知,,
;
故答案为:;
设,则,
,
解得:,
,,
为的中点,
,
;
②当时,
,
,
,
当时,
,
,
,
综上,是定值,定值为.
6.有一位工人师傅将底面直径为,高为的实心圆柱,锻造成底面直径为的实心圆柱,求锻造后圆柱的高是多少?
【答案】.
【分析】设锻造后圆柱的高是,根据体积相等得出方程,再求出即可.
【解答】解:设锻造后圆柱的高是,
则,
解得:,
即锻造后圆柱的高是.
7.将一个底面半径为、高为的“瘦长”圆柱体钢材锻压成底面直径为的“矮胖”圆柱体零件毛坯问:毛坯的高是多少?(列方程解答)
【答案】.
【分析】设毛坯的高为,根据圆柱形钢材的体积相等得出方程解答即可.
【解答】解:设毛坯的高为,
根据题意,得.
解得.
答:毛坯的高是.
8.如图,小明将一个正方形纸片剪去一个宽为5厘米的长条后,再从剩下的长方形纸片上剪去一个宽6厘米的长条,如果两次剪下的长条面积正好相等,那么每一个长条的面积为多少?
【答案】每一个长条的面积为.
【分析】设原来正方形纸的边长是,则第一次剪下的长条的长是,宽是,第二次剪下的长条的长是,宽是;然后根据第一次剪下的长条的面积第二次剪下的长条的面积,列出方程,求出的值是多少,即可求出每一个长条面积为多少.
【解答】解:设原来正方形纸的边长是,则第一次剪下的长条的长是,宽是,第二次剪下的长条的长是,宽是,
由题意得:,
解得:,
则.
答:每一个长条的面积为.
9.一个长,宽,高为的长方体容器中装满了水.小明先把容器中的水倒满2个底面半径为,高为的圆柱体杯子,再把剩下的水全部倒入瓶子甲中.当瓶子甲正放时如图1,瓶内溶液的高度为;瓶子甲倒放时如图2,空余部分的高度为.求瓶子甲的容积.取3,容器的厚度不计)
【答案】.
【分析】设瓶子甲的半径为,根据“长方形容器的水圆柱体杯子水瓶子中水”先列出方程,求出瓶子的半径,再计算瓶子甲的容积.
【解答】解:设瓶子甲的半径为,
由题意,得.
当时,,
.
瓶子甲的容积为
.
答:瓶子甲的容积为.
类型3:工程类应用题
10.为打造“安全、环保、生态”的某河流公园,某市设立若干河流排污治理点(每处需安装相同长度的排污治理管道),一天甲队3名工人去完成5个治理点管道铺设,但还有60米管道未来得及完成,乙队4名工人完成5个治理点后,仍多铺设了40米管道,每名甲队工人比乙队工人每天多铺设20米管道.
(1)求每个排污治理点需铺设的管道长度;
(2)已知每位甲队工人每天需支付费用500元,每名乙队工人每天需支付400元,该市共设立50个排污治理点,另有5880米的同样的污水排放管道也需要安装.现有甲队3名工人,乙队4名工人来安装管道,方案一:全部由甲队安装;方案二:全部由乙队安装;(不到一天按一天算).若要使总费用最少,应选择哪种方案?请通过计算说明.
【答案】(1)120米;
(2)应选择方案二.
【分析】(1)设每个排污治理点需铺设的管道长度为米,根据每名甲队工人比乙队工人每天多铺设20米管道,即可得出关于的一元一次方程,解之即可得出结论;
(2)利用工作时间工作总量每队每天完成的工作量,可分别求出选择各方案所需时间,利用总费用每名工人每天所需费用该队人数工作时间,可分别求出选择各方案所需总费用,比较后即可得出结论.
【解答】解:(1)设每个排污治理点需铺设的管道长度为米,
依题意得:,
解得:.
答:每个排污治理点需铺设的管道长度为120米.
(2)选择方案一所需时间为(天,
选择方案一所需总费用为(元;
选择方案二所需时间为(天,(天,
选择方案二所需总费用为(元.
,
若要使总费用最少,应选择方案二.
11.我区某中学举办一年一届的科技文化艺术节活动,需搭建一个舞台,请来两名工人.已知甲单独完成需4小时,乙单独完成需6小时.现由乙提前做1小时,剩下的工作由甲、乙两人合做,问再合做几小时可以完成这项工作?
【答案】2小时.
【分析】设再合做小时可以完成这项工作,根据“甲工作小时的工作量乙工作小时的工作量总工作量”列方程求解.
【解答】解:设再合做小时可以完成这项工作,根据题意,得:
,
解得:,
答:还需2小时可以完成这项工作.
12.某公司需要加工一批零件,甲每天可以加工16个零件,乙每天可以加工24个零件,甲单独加工这批零件比乙单独加工这批零件多用20天,甲每天的人工费为80元,乙每天的人工费为120元.
(1)问这批零件共有多少个?
(2)在加工零件过程中,公司要派一名质量监督员,并且每天支付他15元补助费,现有三种加工方案:①由甲单独加工这批零件;②由乙单独加工这批零件;③甲、乙合作同时加工这批零件,你认为哪种方案最省钱,为什么?
【答案】(1)960个;(2)方案③.
【分析】(1)设乙单独加工这批零件用天,则甲单独加工这批零件用天,根据此等量关系列出方程求解即可;
(2)应分为三种情况讨论:①由甲单独加工;②由乙单独加工;③由两人共同加工,分别比较三种情况下,所耗时间和花费金额,求出即省钱,又省时间的加工方案.
【解答】解:(1)设乙单独加工这批零件用天,则甲单独加工这批零件用天,
依题意得:,
解得:,
(个,
答:这批零件共有960个;
(2)方案③最省钱,理由如下:
方案①所需费用:(元,
方案②所需费用:(元,
方案③所需工作天数为:天,所需费用为:(元.
选择方案③最省钱.
13.一项工程,甲队单独完成需要40天,乙队单独完成需要50天,现甲队单独做4天后两队合作.
(1)求甲、乙两队合作多少天才能完成该工程.
(2)在(1)的条件下,甲队每天的施工费为3000元,乙队每天的施工费为3500元,求完成此项工程需付给甲乙两队共多少元.
【答案】(1)20天;
(2)142000元.
【分析】(1)设甲、乙两队合作天才能完成该工程,根据总工程量甲单独做4天完成的部分甲、乙合作完成的部分即可得出关于的一元一次方程,解之即可得出结论;
(2)根据总费用单天费用工作时间即可算出甲、乙两队的费用,将其相加即可得出结论.
【解答】解:(1)设甲、乙两队合作天才能完成该工程,
根据题意得:,
解得:.
答:甲、乙两队合作20天才能完成该工程;
(2)甲队的费用为(元,
乙队的费用为(元,
(元.
答:完成此项工程需付给甲乙两队共142000元.
14.甲、乙两队修一座桥,如果由甲队单独完成,需要15天;如果由乙队单独完成,需要30天.现在由甲队单独做了3天后,承办方接到通知,需要加快修桥进度,后续工程由甲、乙两队共同完成,则甲、乙两队后续需要合作多少天才能修完这座桥?
【答案】甲、乙两队后续需要合作8天才能修完这座桥.
【分析】利用甲队单独完成需要15天,乙队单独完成需要30天,可得出每天完成的工作量份数,进而利用总工作量为1得出等式求出答案.
【解答】解:设甲、乙两队合作完成还需要的天数是,根据题意可得:
.
解得:.
答:甲、乙两队后续需要合作8天才能修完这座桥.
类型4:销售类应用题
15.列方程解决问题:
在“双11”促销活动中,某商场一运动品牌店实施如下调价方案:先把每件商品按原价提价后标价,又以6折销售,一套运动服经过上述调价后售价为270元.
(1)这套运动服的原价为多少元?
(2)在促销活动期间,乐乐妈妈到该品牌店购买了3套该运动服,所花的钱比调价方案前优惠了多少元?
【答案】(1)300元;
(2)90元.
【分析】(1)设这套运动服的原价为元,根据调价后售价为270元,可得出关于的一元一次方程,解之即可得出结论;
(2)利用节省的钱数每套节省的钱数购买数量,即可求出结论.
【解答】解:(1)设这套运动服的原价为元,
根据题意得:,
解得:.
答:这套运动服的原价为300元;
(2)
(元.
答:所花的钱比调价方案前优惠了90元.
16.小明用的练习本可以到甲、乙两家商店购买,已知两商店的标价都是每本2元,甲商店的优惠条件是购买10本以上,从第11本开始按标价的出售;乙商店的优惠条件是,从第一本起按标价的出售.若小明要购买本练习本.
(1)则当小明到甲商店购买时,需付款 元;当到乙商店购买时,需付款 元;
(2)买多少本练习本时,两家商店花费相同?
(3)小明准备买50本练习本,为了节约开支,选择哪家更划算?
【答案】(1),;
(2)30本;
(3)选择甲商店更划算.
【分析】(1)利用总价单价数量,结合两家商店给出的优惠条件,即可用含的代数式表示出到两家商店购买所需费用;
(2)根据两家商店花费相同,即可得出关于的一元一次方程,解之即可得出结论;
(3)分别将代入和中可求出到两家商店购买所需费用,比较后即可得出结论.
【解答】解:(1)依题意得:小明到甲商店购买需付款(元;
小明到乙商店购买需付款(元.
故答案为:;.
(2)依题意得:,
解得:.
答:买30本练习本时,两家商店花费相同.
(3)当时,;
当时,.
,
选择甲商店更划算.
17.忠县重百电商通过互联网销售某品牌电话手表,第一周的总销售额为5520元,第二周的总销售额为6840元,第二周比第一周多售出22块电话手表.
(1)求每块电话手表的售价;
(2)该公司在第三周将每块电话手表的售价降低了,并预计第三周能售出158块电话手表,由于恰逢开学周,不少家庭为子女购买电话手表,该款手表在第三周的销量比预计还多了.如果每块电话手表成本为42元,该公司第三周销售手表的总利润为3318元,求的值.
【答案】(1)每块电话手表的售价为60元;
(2)的值为25.
【分析】(1)设每块电话手表的售价为元,利用总销售额销售单价销售数量,结合第一周及第二周总销售额及销售数量间的关系,可得出关于的一元一次方程,解之即可得出结论;
(2)利用总利润每块电话手表的销售利润第三周的销售数量,可得出关于的一元一次方程,解之即可得出的值.
【解答】解:(1)设每块电话手表的售价为元,
根据题意得:,
解得:.
答:每块电话手表的售价为60元;
(2)根据题意得:,
整理得:,
解得:.
答:的值为25.
18.平价商场恰好用3800元购进甲,乙两种商品共50件,若甲种商品每件进价70元,乙种商品每件进价80元,且统一标价120元出售.
(1)求购进甲、乙两种商品各多少件?
(2)该商场售出这批商品的一部分后,恰逢“元旦”对剩余商品进行促销,以标价的8折售完所有剩余商品,共获利1480元,且促销商品中乙的件数是甲件数的1.5倍,求促销商品中甲商品有多少件?
【答案】(1)购进甲种商品20件,乙种商品30件;
(2)促销商品中甲商品有12件.
【分析】(1)设购进甲种商品件,则购进乙种商品件,利用总价单价数量,可得出关于的一元一次方程,解之可得出购进甲种商品的数量,再将其代入中,即可求出购进乙种商品的数量;
(2)设促销商品中甲商品有件,则乙商品有件,利用总利润销售单价销售数量进货总价,可得出关于的一元一次方程,解之即可得出结论.
【解答】解:(1)设购进甲种商品件,则购进乙种商品件,
根据题意得:,
解得:,
.
答:购进甲种商品20件,乙种商品30件;
(2)设促销商品中甲商品有件,则乙商品有件,
根据题意得:,
解得:.
答:促销商品中甲商品有12件.
19.“广交会”是中国历史最长的综合性国际贸易盛会.在“广交会”中,某到会采购商计划从厂家购进甲、乙两种商品.已知甲种商品的每件进价比乙种商品的每件进价少20元.若购进甲种商品5件,乙种商品3件,共需要700元.
(1)求甲、乙两种商品的每件进价分别是多少元?
(2)该采购商从厂家购进了甲种商品3万件、乙种商品2万件.在销售时,甲种商品的每件售价为110元,要使得这5万件商品所获利润率为,求每件乙种商品的售价是多少元?
【答案】(1)甲种商品的进价80元,则乙种商品的进价100元.
(2)每件乙种商品的售价是121元.
【分析】(1)设甲种商品的进价元,则乙种商品的进价元,根据“购进甲种商品5件,乙种商品3件,共需要700元”可列出方程,求解即可;
(2)设乙种商品的售价为元,根据“使得这5万件商品所获利润率为”列出方程,求解即可.
【解答】解:(1)设甲种商品的进价元,则乙种商品的进价元,
根据题意,得.
解得.
则.
答:甲种商品的进价80元,则乙种商品的进价100元;
(2)设乙种商品的售价为元,
根据题意,得.
解得.
答:每件乙种商品的售价是121元.
类型5:比赛类应用题
20.为了迎接世界杯足球赛的到来,足球协会举办了一次足球赛,其中得分规则及奖励方案如表:
胜一场 平一场 负一场
积分 3 1 0
人均奖金 1500元 700元 0
当比赛进行到每队比赛完12场时,队共积分20分,并且没有负一场.
(1)试判断队胜、平各几场?
(2)每赛一场,队每名队员均得出场费500元,那么比赛完12场后,队每名队员所得奖金与出场费累计为多少元?
【答案】(1)队胜4场,平8场;
(2)出场费加奖金一共17600元.
【分析】(1)设队胜利场,则平了场,根据总积分为20分列出方程即可求解;
(2)根据(1)中求得胜场数和平场数计算每名队员的奖金和出场费的总和即可解题.
【解答】解:(1)设队胜利场,
一共打了12场,
平了场,
,
解得:,(场.
答:队胜4场,平8场.
(2)每场比赛出场费500元,12场比赛出场费共6000元,
赢了4场,奖金为元,
平了8场,奖金为元,
奖金加出场费一共17600元;
答:一共赢了4场,出场费加奖金一共17600元.
21.在2022年女足亚洲杯决赛中,中国女足以逆转韩国女足,时隔16年再夺亚洲杯冠军!某学校掀起一股足球热,举行了班级联赛,九(1)班开局11场保持不败,共积23分,按照比赛规则,胜一场积3分,平一场积1分,负一场积0分,求该班获胜的场数.
【答案】6场.
【分析】设九(1)班获胜场,则平场,根据九(1)班开局11场共积23分,即可得出关于的一元一次方程,解之即可得出结论.
【解答】解:设九(1)班获胜场,则平场,
根据题意得:,
解得:.
答:九(1)班获胜6场.
22.篮球运动是最流行的运动之一,深受青少年喜爱.某市举办春季校园篮球赛,共有八支队伍参赛,其中三支队伍的积分表如下.请根据表格信息解答下列问题:
队名 比赛场次 胜场 负场 积分
前进 14 10 4 24
光明 14 9 5 23
远方 14 0 14 14
(1)请回答:胜一场得 2 分,负一场得 分;
(2)若某队胜场总积分是负场总积分的2倍,求该队的胜场数;
(3)若某队的负场总积分是胜场总积分的正整数倍,求该队的胜场数.
【答案】(1)2,1;
(2)能,胜7场;
(3)2场.
【分析】(1)设胜一场积分,则负一场积分,依照光明队的胜负场次及得分情况可列出一元一次方程,求解即可;
(2)设胜场数是,负场数是,结合(1)中结论,根据胜场总积分是负场总积分的2倍,列一元一次方程求解即可;
(3)设胜场数是,负场数是,列方程解出,根据数的整除特性及奇偶性可得答案.
【解答】解:(1)设胜一场积分,则负一场积分,
依题意得:,
解得,
此时,
胜一场积2分,负一场积1分.
故答案为:2,1;
(2)答:能.理由如下:
设胜场数是,负场数是,
依题意得:,
解得,
1,,
答:该队胜7场;
(3)设胜场数是,负场数是,
依题意得:,
解得:,
是正整数,是奇数,
符合题意的有:,,.
答:该队胜的场数是2场.
23.在一次知识竞赛中,甲、乙两班各有50位同学参加比赛,每位同学都需要完成三道题的答题,竞赛规则为:“答对一题得10分,不答或者答错扣10分”.
(1)请直接写出每位同学所有可能的得分情况;
(2)甲班的答题情况为:有2位同学全部答错,全对的人数是答对1题人数的3倍少6人,答对两题的人数是答对1题人数的2倍;乙班的答题情况为:没有同学全部答错,答对一题人数的3倍和答对2题的人数之和等于全部答对的人数.
①求甲班全部答对的人数;
②请判断甲乙两班哪个班的得分更高,并说明理由.
【答案】(1)分、分、10分和30分;
(2)①21人;
②乙班得分高.
【分析】(1)根据竞赛的得分规则可得答案;
(2)①设甲班答对1题的有人,根据题意列出方程,解方程可得答案;
②首先算出甲班的得分,设乙班全部答对的有人,答对1题的有人,答对2题的有人,整理可得乙班的得分,再比较可得结论.
【解答】解:(1)若只答对1题,则不答或答错2题,得分为:,
若只答对2题,则不答或答错1题,得分为:,
若只答对3题,得分为:,
若不答或答错3题,得分为:,
答:每位同学所有可能的得分情况是分、分、10分和30分;
(2)①设甲班答对1题的有人,
由题意得,,
解得,
(人,
答:甲班全部答对的人数是21人;
②乙班得分更高.
由题意得,甲班答对3题有21人,答对2题的有18人,答对1题的有9人,全部答错的有2人,
故甲班的得分为(分,
设乙班全部答对的有人,答对1题的有人,答对2题的有人,
所以,
即,
故乙班得分为(分,
,
答:乙班得分更高.
24.2022世界杯于11月21日在卡塔尔召开.在小组赛阶段,32支球队根据自身实力所处的不同档次,以及所属大洲的情况进行抽签选择,每个小组4支球队.在小组内部的球队会和其他三支队伍都进行比赛,以下是世界杯小组赛组的积分表.
小组 代表队 场次(场 胜(场 平(场 负(场 积分(分
组 荷兰 3 2 1 0 7
塞内加尔 3 2 0 1 6
厄瓜多尔 3 1 1 1 4
卡塔尔 3 0 0 3 0
(说明:积分胜场积分平场积分负场积分)
(1)求小组赛中胜一场、平一场、负一场各积多少分?
(2)小组赛结束时,阿根廷队没有平场,并且小组赛积分6分,成功晋级,求阿根廷队胜、负各多少场?
(3)在本次小组赛中,能否出现一支球队保持不败的战绩,且胜场总积分恰好等于它的平场总积分?
【答案】(1)胜一场积3分,平一场积1分,负一场积0分;
(2)胜2场,负1场;
(3)不能出现一支球队保持不败的战绩,且胜场总积分恰好等于它的平场总积分.
【分析】(1)根据表格数据,可得负一场积0分,然后设胜一场积分,平一场积分,列方程即可解答;
(2)设阿根廷队胜场,则负场,根据题意列方程即可解答;
(3)设一个队胜场,则平场,根据题意列方程即可解答.
【解答】解:(1)观察积分表,从卡塔尔一行数据可以看出:负一场积0分,
设胜一场积分,从塞内加尔一行数据可得:
,
解得:,
设平一场积分,从荷兰一行数据可得:
,
解得:,
所以,小组赛中胜一场积3分,平一场积1分,负一场积0分,
答:小组赛中胜一场积3分、平一场积1分、负一场积0分;
(2)设阿根廷队胜场,则负场,由题意得:
,
解得:,
(场,
答:阿根廷队胜2场,负1场;
(3)设一个队胜场,则平场,由题意可知,胜场总积分等于平场总积分,得方程:
,
解得:,
(胜场数)的值必须为整数,
不合实际.
答:不能出现一支球队保持不败的战绩,且胜场总积分恰好等于它的平场总积分.
类型6:行程类应用题
25.甲、乙两队相约沿相同的路线徒步,徒步的路程为,甲队步行速度为,乙队步行速度为,甲队出发后,乙队才出发.
(1)问乙队需要多长时间可以追上甲队;
(2)从甲队出发开始到乙队完成徒步路程止,甲队出发多长时间,两队间隔的路程为.
【答案】(1)2小时;
(2)小时或2小时或4小时.
【分析】(1)设小时后乙队可以追上甲队,根据路程相等列方程求解即可;
(2)分追上甲队前和追上甲队后相距两种情况,分别列方程求解即可.
【解答】解:(1)设小时后乙队可以追上甲队,
根据题意得,,
解得,
答:2小时后乙队可以追上甲队;
(2)设甲队出发小时,两队间隔的路程为,
①乙未出发前,根据题意得,,
解得,
②甲乙均出发且未相遇,根据题意得,,
解得,
③甲乙均出发且相遇后,根据题意得,,
解得,
答:甲队出发小时或2小时或4小时,两队间隔的路程为.
26.已知数轴上两点、对应的数分别为、4,点为数轴上一动点.
(1)若点到点、点的距离相等,求点对应的数;
(2)数轴上是否存在点,使点到点、点的距离之和为18?若存在,请求出点所表示的数;若不存在,说明理由;
(3)现在点以3个单位长度秒的速度向右运动,点以1个单位长度秒的速度向左运动,点以2个单位长度秒的速度从点向右运动.点、、三点同时运动,当点与点之间的距离为4个单位长度时,求点所对应的数是多少?
【答案】(1)点对应的数为;
(2)点对应的数为8或;
(3)点对应的数为3或7.
【分析】(1)点到点、点的距离相等,即点为线段的中点,以此即可求解;
(2)设点对应的数为,分两种情况:①当点在点的右侧时,根据两点间距离公式列出方程求解;②当点在点的左侧时,根据两点间距离公式列出方程求解;
(3)设运动时间为秒,分两种情况:①当点在点左侧,点与点之间的距离为4个单位长度时;②当点在点右侧,点与点之间的距离为4个单位长度时;分别列出方程,求解即可.
【解答】解:(1)点到点、点的距离相等,
点为线段的中点,
点对应的数为:;
(2)设点对应的数为,
①当点在点的右侧时,
根据题意得:,
解得:,
②当点在点的左侧时,
根据题意得:,
解得:,
综上,点对应的数为8或;
(3)设运动时间为秒,则点对应的数为,点对应的数为,点对应的数为,
①当点在点左侧,点与点之间的距离为4个单位长度时,
,
解得:,
此时,点对应的数为,
②当点在点右侧,点与点之间的距离为4个单位长度时,
,
解得:,
此时,点对应的数为,
综上,点对应的数为3或7.
27.小明爸爸骑着摩托车带着小明在公路上匀速行驶,如表是小明每隔1小时看到的里程情况,你能确定小明在时看到的里程碑上的数吗?
时间 里程情况
是一个两位数字,它的两个数字之和为7.
十位与个位数字与时所看到的正好颠倒了.
比时看到的两位数中间多了个0.
如果设小明在时看到的数的十位数字是,那么根据以上信息回答下列问题:(结果均要化简)
(1)时小明看到的数可表示为 ;
(2)时小明看到的数可表示为 ,间摩托车行驶的路程是 ;
(3)时小明看到的数可表示为 ,问摩托车行驶的路程是 ;
(4)利用一元一次方程求出小明在时看到的里程碑上的数是多少?
【答案】(1);
(2),;
(3),;
(4)16.
【分析】(1)由小明在看到的两位数的两个数字之和为7及十位数字为,可得出小明在时看到的数的个位数字是,利用小明在时看到的数十位数字个位数字,即可用含的代数式表示出小明在时看到的数;
(2)利用小明在时看到的数个位数字十位数字,可用含的代数式表示出小明在时看到的数,再利用间摩托车行驶的路程小明在时看到的数小明在时看到的数,即可用含的代数式表示出间摩托车行驶的路程;
(3)利用小明在时看到的数十位数字个位数字,可用含的代数式表示出小明在时看到的数,再利用间摩托车行驶的路程小明在时看到的数小明在时看到的数,即可用含的代数式表示出间摩托车行驶的路程;
(4)根据摩托车的行驶速度不变,可得出关于的一元一次方程,解之即可求出的值,再将其代入中即可求出结论.
【解答】解:(1)小明在看到的数是一个两位数字,它的两个数字之和为7,小明在时看到的数的十位数字是,
小明在时看到的数的个位数字是,
小明在时看到的数是.
故答案为:;
(2)根据题意得:时小明看到的数是,
间摩托车行驶的路程是.
故答案为:,;
(3)根据题意得:时小明看到的数是,
问摩托车行驶的路程是.
故答案为:,;
(4)根据题意得:,
解得:,
.
答:小明在时看到的里程碑上的数是16.
28.如图在数轴上点表示数,点表示数,、满足.
(1)点表示的数为 ;点表示的数为 ;
(2)若在原点处放一挡板,一小球甲从点处以1个单位秒的速度向左运动;同时另一小球乙从点处以3个单位秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为(秒,
①当时,甲小球到原点的距离 ;乙小球到原点的距离 ;
当时,甲小球到原点的距离 ;乙小球到原点的距离 ;
②试探究:甲,乙两小球到原点的距离可能相等吗?若不能,请说明理由若能,请求出甲,乙两小球到原点的距离相等时的值.
③若当甲和乙开始运动时,挡板也从原点以1个单位秒的速度向右运动,直接写出甲,乙两小球到挡板的距离相等时的值.
【答案】(1),4;
(2)①3,1,4,2;
②当秒或秒时,甲乙两小球到原点的距离相等;
③.
【分析】(1)利用绝对值的非负性即可确定出,即可;
(2)①根据运动确定出运动的单位数,即可得出结论;
②根据,(Ⅱ),根据甲、乙两小球到原点的距离相等列出关于的方程,解方程即可;
③分当都向左运动时时,当反弹时,表示出甲、乙两小球之间的距离即可.
【解答】解:(1),
,,
点表示的数为,点表示的数为4,
故答案为:,4;
(2)①当时,
一小球甲从点处以1个单位秒的速度向左运动,
甲小球1秒钟向左运动1个单位,此时,甲小球到原点的距离,
一小球乙从点处以3个单位秒的速度也向左运动,
乙小球1秒钟向左运动3个单位,此时,乙小球到原点的距离,
当时,
一小球甲从点处以1个单位秒的速度向左运动,
甲小球1秒钟向左运动2个单位,此时,甲小球到原点的距离,
一小球乙从点处以3个单位秒的速度也向左运动,
乙小球1秒钟向左运动6个单位,此时,乙小球到原点的距离,
故答案为:3,1,4,2;
②当时,得,
解得;
当时,得,
解得;
故当秒或秒时,甲乙两小球到原点的距离相等;
(3)碰到挡板需要(秒,碰到挡板需要(秒,
时,甲,乙两小球到挡板的距离相等,
①都向左运动时,则,即,
解得,
②反弹时,则,即,
当时,不符合题意舍去,
值为时,甲,乙两小球到挡板的距离相等.
29.如图,已知线段,点为线段上一点,且.动点以的速度,从点出发,沿方向运动,运动到点停止;点出发后,点以的速度,从点出发,沿方向运动,运动到点时,停留,按原速沿方向运动到点停止.设的运动时间为.
(1) 8 , ;
(2)当从向运动时,若,求的值.
(3)当时,直接写出的值.
【答案】(1)8,16;
(2)当从向运动时,若,的值为2;
(3)当时,的值为或或10.
【分析】(1)根据,即可解答;
(2)根据运动时间和运动速度可用含的代数式表示出点、表示的数,再根据列出方程,求解即可;
(3)先求出点追上点的时间,再分三种情况:①当时,即向运动,;②当时,即从向运动,且点在点的左侧,;③当时,即从向运动,且点在点的右侧,;根据不同情况列出方程,再求解即可.
【解答】解:线段,,
,
,
故答案为:8,16;
(2)设的运动时间为,
当从向运动时,点表示的数为,点表示的数为,
则,,
,
,
解得:,
当从向运动时,若,的值为2;
(3)当点追上点时,可得:,
解得:,
①当时,即向运动,,
此时,点表示的数为,点表示的数为,
则,
,
解得:;
②当时,即从向运动,且点在点的左侧,,
此时,点表示的数为,点表示的数为,
则,
,
解得:;
③当时,即从向运动,且点在点的右侧,,
此时,点表示的数为,点表示的数为,
则,
,
解得:;
综上,当时,的值为或或10.
类型7:环形跑道与时钟问题
30.钟表是我们日常生活中常用的计时工具.如图,在圆形钟面上,把一周等分成12个大格,每个大格等分成5个小格,分针和时针均绕中心匀速转动.(本题中的角均指小于的角),
(1)分针每分钟转 6 度,时针每分钟转 度,当时间为时,分针和时针的夹角为 度;
(2)求开始后几分钟分针第一次追上时针;
(3)点为4点钟的位置,平分,平分,从开始计时,分钟后,,求的值.
【答案】(1)6,0.5,75;
(2);
(3)分钟或分钟后,.
【分析】(1)根据圆周是,分别计算时针和分针的转速即可,再根据时时针和分针夹角是2.5个大格计算夹角度数即可;
(2)设分钟后分针第一次追上时针,根据题意列方程求解即可;
(3)根据题意分情况列方程求解即可.
【解答】解:(1)分针每分钟转,时针每分钟转,
时时针和分针夹角是2.5个大格,
时,分针和时针的夹角为,
故答案为:6,0.5,75;
(2)设分钟后分针第一次追上时针,
由题意得,,
解得,
分钟后分针第一次追上时针;
(3)①没追上之前,由题意知,,
解得,
②超过之后,由题意知,,
解得,
分钟或分钟后,.
31.已知环形跑道一圈长为400米,小丽与小杰的速度之比为,如果小丽和小杰在跑道上相距8米处同时反向出发,经过28秒后两人首次相遇,求两人的速度各是多少?
【答案】小丽的速度为6米秒,小杰的速度为8米秒.
【分析】设小丽的速度为米秒,则小杰的速度为米秒,利用路程速度时间,结合经过28秒后两人首次相遇,即可得出关于的一元一次方程,解之即可得出的值,再将其代入和中即可求出结论.
【解答】解:设小丽的速度为米秒,则小杰的速度为米秒,
依题意得:,
解得:,
(米秒),(米秒).
答:小丽的速度为6米秒,小杰的速度为8米秒.
32.周末小明和爸爸在的环形跑道上骑车锻炼,他们在同一地点沿着同一方向同时出发,骑行结束后两人有如下对话:
(1)请根据他们的对话内容,求出小明的骑行速度;
(2)爸爸第一次追上小明后,在第二次相遇前,再经过多少分钟,小明和爸爸在跑道上相距?
【答案】(1)150米分钟;
(2)分钟或分钟.
【分析】(1)设小明的骑行速度为米分钟,则爸爸的骑行速度为米分钟,根据爸爸2分钟才能第一次追上小明,即可得出关于的一元一次方程,解之即可得出结论;
(2)设在第二次相遇前,再经过分钟,小明和爸爸在跑道上相距100米,分爸爸又比小明多骑了100米及爸爸又比小明多骑了米两种情况考虑,利用路程速度时间,即可得出关于的一元一次方程,解之即可得出结论.
【解答】解:(1)设小明的骑行速度为米分钟,则爸爸的骑行速度为米分钟,
依题意得:,
解得:.
答:小明的骑行速度为150米分钟.
(2)设在第二次相遇前,再经过分钟,小明和爸爸在跑道上相距100米,
①爸爸又比小明多骑了100米,
依题意得:,
解得:;
②爸爸又比小明多骑了米,
依题意得:,
解得:.
答:在第二次相遇前,再经过分钟或分钟,小明和爸爸在跑道上相距100米.
33.周末,小明和爸爸在400米的环形跑道上骑车锻炼,他们在同一地点沿着同一方向同时出发,骑行结束后两人有如下对话:
请根据他们的对话内容,求小明和爸爸的骑行速度.
【答案】小明的骑行速度为200米分,爸爸的骑行速度为400米分.
【分析】设小明的骑行速度为米分,则爸爸的骑行速度为米分,根据距离速度差时间即可得出关于的一元一次方程,解之即可得出结论.
【解答】解:设小明的骑行速度为米分,则爸爸的骑行速度为米分,
根据题意得:,
解得:,
.
答:小明的骑行速度为200米分,爸爸的骑行速度为400米分.
34.正方形的轨道上有两个点甲与乙,开始时甲在处,乙在处,它们沿着正方形轨道顺时针同时出发,甲的速度为每秒,乙的速度为每秒.
已知正方形轨道的边长为,求乙在第5次追上甲时在哪条线段上?
【答案】线段上.
【分析】设乙走秒第一次追上甲,设乙再走秒第二次追上甲.根据题意分别列一元一次方程,然后寻找规律解题.
【解答】解:设乙走秒第一次追上甲.
根据题意,得.
解得.
乙走1秒第一次追上甲,则乙在第1次追上甲时的位置是上;
设乙再走秒第二次追上甲.
根据题意,得,
解得.
乙再走2秒第二次追上甲,则乙在第2次追上甲时的位置是上;
同理:乙再走2秒第三次次追上甲,则乙在第3次追上甲时的位置是上;
乙再走2秒第四次追上甲,则乙在第4次追上甲时的位置是上;
乙在第5次追上甲时的位置又回到线段上.
类型8:方案选择类问题
35.永辉超市为春节促销,特推出了两种购物方案.
方案一:非会员购物所有商品价格可获九折优惠;
方案二:如交纳400元会费成为该超市会员,则所有商品价格可获八五折优惠.
(1)以(元表示商品价格,分别用含有的式子表示出两种购物方案中支出金额;
(2)若某人计划在超市购买价格为5800元的电视机一台,请分析选择哪种方案更省钱?
(3)哪种情况下,两种方案的支出金额相同?
【分析】(1)根据题意列出代数式即可;
(2)根据两种方案算出支出金额即可;
(3)根据题意列出方程即可求出的值.
【解答】解:(1)方案一的支出金额为:,
方案二的支出金额为:;
(2)当时,
,
,
答:方案一更为省钱;
(3)当,
解得:,
答:当时,两种方案的支出金额相同
36.某校七年级准备观看电影《长津湖》,由各班班长负责买票,每班人数都多于40人,票价每张30元,一班班长问售票员买团体票是否可以优惠,售票员说:40人以上的团体票有两种优惠方案可选择:方案一:全体人员可打8折;方案二:若打9折,有5人可以免票.
(1)若二班有42名学生,则他该选择哪个方案?
(2)一班班长思考一会儿说,我们班无论选择哪种方案要付的钱是一样的,你知道一班有多少人吗?
【分析】(1)分别计算出方案一和方案二的花费,然后比较大小即可解答本题;
(2)设一班有人,根据已知得出两种方案费用一样,进而列出方程求解即可.
【解答】解:(1)由题意可得,
方案一的花费为:(元,
方案二的花费为:(元,
,
若二班有42名学生,则他该选选择方案二;
(2)设一班有人,根据题意得,
,
解得.
答:一班有45人.
37.下表是中国电信两种” 套餐”计费方式.(月基本费固定收,主叫不超主叫时间,流量不超上网流量不收费,主叫超时和上网超流量部分加收超时费和超流量费)
月基本费元 主叫通话分钟 上网流量 接听 主叫超时部分(元分钟) 超出流量部分(元
方式一 49 200 500 免费 0.20 0.15
方式二 69 250 600 免费 0.15 0.1
(1)若某月小萱主叫通话时间为220分钟,上网流量为,则她按方式一计费需 98 元,按方式二计费需 元,所以她应该选择方式 ;
(2)若小萱某月主叫通话时间为100分钟,是否存在某上网流量,按方式一和方式二的计费相等?若存在,请求出的值:若不存在,请说明理由.
(3)若小萱每月主叫通话时间在100分钟以内,要选择更低的计费方式,请你帮助她做出选择,直接写出结果即可.
【答案】(1)98,89,二;
(2)存在,理由见解析;
(3)当上网流量未超过时,应选择方式一,当上网流量超过时,应选择方式二.
【分析】(1)根据表格中的数据分别计算出两种计费方式所需费用,再进行比较即可解答;
(2)分,,三种情况,分别列出方程,解出即可求解;
(3)分析(2)中结果,即可得出结论.
【解答】解:(1)方式一:
(元,
方式二:
(元,
,
她应该选择方式二;
故答案为:98,89,二;
(2)存在,理由如下:
①当时,
方式一计费需49元,方式而计费需69元,
,
不符合题意;
②当时,
根据题意得:,
解得:(舍去);
③当时,
根据题意得:,
解得:;
综上,当上网流量为,按方式一和方式二的计费相等.
(3)由(2)可知,当上网流量未超过时,应选择方式一,当上网流量超过时,应选择方式二.
38.某校体育社团由于报名人数激增,决定从某体育用品店购买若干足球和篮球,用于日常训练.已知每个篮球的价格比每个足球的价格多30元,用900元购买足球的数量是用720元购买篮球数量的2倍.
(1)求篮球和足球的单价各是多少?
(2)根据学生报名情况,社团需一次性购买篮球和足球共80个,且要求购买足球数量不超过篮球数量的请问社团购买多少个篮球时,能使购买费用最少?
【答案】(1)篮球的单价是80元,足球的单价是50元;
(2)社团购买60个篮球时费用最少,最少费用为5800元.
【分析】(1)设足球的单价是元,则篮球的单价是元,根据用900元购买足球的数量是用720元购买篮球数量的2倍列出方程,解方程即可;
(2)设学校可以购买个篮球,则可以购买个足球,购买费用为元,根据总费用购买篮球和足球费用的和列出函数解析式,再根据购买足球数量不超过篮球数量的,求出的取值范围,再根据函数的性质求最值.
【解答】解:(1)设足球的单价是元,则篮球的单价是元,
根据题意,得,
解得,
经检验,是原方程的解,且符合题意,
.
答:篮球的单价是80元,足球的单价是50元;
(2)设学校购买个篮球,则购买足球个,购买费用为元,
则,
购买足球数量不超过篮球数量的,
,
解得,
,
当时,有最小值,最小值为5800元,
此时,
答:社团购买60个篮球时费用最少,最少费用为5800元.
39.2021年“双十一”期间,很多国货品牌受到人们的青睐,销量大幅增长.某平台的体育用品旗舰店实行优惠销售,规定如下:对原价160元件的某款运动速干衣和20元双的某款运动棉袜开展促销活动,活动期间向客户提供两种优惠方案.
方案:买一件运动速干衣送一双运动棉袜;
方案:运动速干衣和运动棉袜均按9折付款.
某户外俱乐部准备购买运动速干衣30件,运动棉袜双.
(1)若该户外俱乐部按方案购买,需付款 元(用含的式子表示);若该户外俱乐部按方案购买,需付款 元(用含的式子表示);
(2)若,通过计算说明此时按哪种方案购买较为合算;
(3)当购买运动棉袜多少双时两种方案付款相同.
【答案】(1),;
(2)按方案购买较为合算;理由见解答部分;
(3)当购买运动棉袜60双时,两种方案付款相同.
【分析】(1)根据两种不同的优惠方案列出代数式即可;
(2)将分别代入(1)所列代数式计算比较即可;
(3)根据“两种方案付款相同”列出方程并解答.
【解答】解:(1)按方案购买,需付款:,
即需要付款元;
按方案购买,需付款:,
即需要付款元.
故答案为:,;
(2)当时,
方案(元.
方案(元.
因为,所以按方案购买较为合算;
(3)根据题意,得.
解得.
答:当购买运动棉袜60双时,两种方案付款相同.
类型9:储蓄、利息问题
40.小希准备在6年后考上大学时,用15000元给父母买一份礼物表示感谢,决定现在把零花钱存入银行.下面有两种储蓄方案:
①直接存一个6年期.年期年利率为
②先存一个3年期,3年后本金与利息的和再自动转存一个3年期.年期年利率为
你认为按哪种储蓄方案开始存入的本金比较少?请通过计算说明理由.
【分析】设储蓄方案①所需本金元,储蓄方案②所需本金元,根据本息和本金利率期数),即可得出关于的一元一次方程,解之即可得出的值,比较后即可得出结论.
【解答】解:设储蓄方案①所需本金元,储蓄方案②所需本金元.
依题意,得:,,
解得:,,
,
按照储蓄方案①开始存入的本金比较少.
41.小明的爸爸开了一家运动品商店,近期商店购进一批运动服,按进价提高后打八折出售,这时每套运动服的售价为140元.
(1)求每套运动服的进价?
(2)运动服卖出一半后,正好赶上双十一促销,商店决定将剩下的运动服每3套400元的价格出售,很快销售一空,后一半促销获利5000元,求小明的爸爸共购进多少套运动服?
(3)最后,小明的爸爸决定将整批运动服的利润当做小明的教育基金存入银行,已知该银行3年期的固定储蓄年利率为,求3年后取出的本息和为多少元?
【分析】(1)设每套运动服的进价为元,根据打折后每套运动服的售价为140元,即可得出关于的一元一次方程,解之即可得出结论;
(2)设小明的爸爸共购进套运动服,根据后一半促销获利5000元,即可得出关于的一元一次方程,解之即可得出结论;
(3)根据本息和本金利润率年限),即可求出结论.
【解答】解:(1)设每套运动服的进价为元,
依题意,得:,
解得:.
答:每套运动服的进价为125元.
(2)设小明的爸爸共购进套运动服,
依题意,得:,
解得:.
答:小明的爸爸共购进1200套运动服.
(3)(元.
答:3年后取出的本息和为15134元.
42.妈妈为小华存了一个3年期的教育储蓄(设3年期的年利率为,3年后能取10350元,妈妈开始存入了多少元?
【分析】设妈妈开始存入了元,根据本金本金利率时间列出方程,解方程即可.
【解答】解:设妈妈开始存入了元,根据题意得,
,
解得,.
答:妈妈开始存入了9000元.
43.小明的爸爸三年前为小明存了一份3000元的教育储蓄.今年到期时取出,得本利和为3243元.请你帮小明算一算这种储蓄的年利率.
【分析】不用交利息税的本利和计算方法为:本利和本金本金年利率时间,利用本利和为3243元作为相等关系列方程求解即可.
【解答】解:设这种储蓄的年利率为,
则:,
解之得:.
即.
答:这种储蓄的年利率为.
44.李明存入银行一笔钱,整存整取3年,年利率,到期后共取出5375元,求李明存入了多少钱?
【答案】李明存入5000元.
【分析】设李明存入元,根据本息和本金年份年利率本金,即可得出关于的一元一次方程,解之即可得出结论.
【解答】解:设李明存入元,则
,
解得,
答:李明存入5000元.
一 类型10:产品配套问题
45.用白铁皮做罐头盒,每张铁皮可制盒身25个,或制盒底40个,一个盒身与两个盒底配成一套.现在有36张白铁皮,用多少张制盒身,多少张制盒底,可使盒身与盒底正好配套?
【分析】可设用张制盒身,则张制盒底,可使盒身与盒底正好配套,根据等量关系:一个盒身与两个盒底配成一套.列出方程求解即可.
【解答】解:设用张制盒身,则张制盒底,
根据题意,得到方程:,
解得:,
.
答:用16张制盒身,20张制盒底,可使盒身与盒底正好配套.
46.列方程,解应用题:
新型冠状肺炎疫情正在全球蔓延肆虐,口罩成了人们生活中必不可少的物品,某口罩厂有40名工人,每人每天可以生产1000个口罩面或1200根耳绳.一个口罩面需要配两根耳绳,为使每天生产的口罩面与耳绳刚好配套,应安排多少名工人生产口罩面?
【分析】根据人每天可以生产1000个口罩面或1200根耳绳,一个口罩面需要配两根耳绳,可以列出相应的方程,然后解方程,即可解答本题.
【解答】解:设应安排名工人生产口罩面,则安排名工人生产耳绳,
,
解得,
答:应安排15名工人生产口罩面.
47.疫情防控期间,口罩成为人们生活中必不可少的物品.某口罩厂有87名工人,每人每天可以生产900个口罩面或1100个口罩耳绳,一个口罩面需要配两个耳绳.
(1)为使每天生产的口罩面和口罩耳绳刚好配套,应安排多少名工人生产口罩面?
(2)若该工厂某天生产的口罩面与口罩耳绳刚好配套,设一个成品口罩成本价是元,售价是元,请用含、的式子表示该口罩厂该天生产口罩的利润.
【答案】(1)应安排33名工人生产口罩面;
(2)该口罩厂该天生产口罩的利润为元.
【分析】(1)设安排名工人生产口罩面,则有名工人生产口罩耳绳,根据每天生产的口罩面和口罩耳绳刚好配套列出方程,解出方程即可得到答案;
(2)由(1)可算出该天生产成品口罩的数量,再根据利润(单个售价单个成本)数量列出代数式即可得到答案.
【解答】解:(1)设安排名工人生产口罩面,则有名工人生产口罩耳绳,
根据题意得:,
解得:,
应安排33名工人生产口罩面;
(2)由(1)可得,该天生产成品口罩的数量为:(个,
则该口罩厂该天生产口罩的利润为:元.
48.用相同规格的正方形硬纸板做成如图1的直三棱柱盒子,每个盒子由3个相同的长方形做侧面和2个相同的正三角形做底面组成,硬纸板按如图2的两种方法裁剪(裁剪后边角料不再利用).
方法:剪出6个侧面;方法:剪出4个侧面和5个底面.
现有19张这种规格的正方形硬纸板,裁剪时张用方法,其余用方法.
(1)用含的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,则能做多少个盒子?
【答案】(1)裁剪出个侧面,个底面;
(2)能做30个盒子.
【分析】(1)由正方形硬纸板的张数及按方法裁剪的张数,可得出裁剪时张用方法,结合两种方法裁剪出的侧面及底面的数量,即可用含的代数式表示出裁剪出的侧面和底面的个数;
(2)由每个盒子由3个侧面和2个底面组成,结合裁剪出的侧面和底面恰好全部用完,可得出关于的一元一次方程,解之可得出的值,再将其代入中,即可求出结论.
【解答】解:(1)共有19张这种规格的正方形硬纸板,且裁剪时张用方法,
裁剪时张用方法,
裁剪出个侧面,个底面.
裁剪出个侧面,个底面;
(2)根据题意得:,
解得:,
.
答:能做30个盒子.
49.在手工制作课上,老师组织七年级(2)班的学生用硬纸制作圆柱形茶叶筒.七年级(2)班共有学生44人,其中男生人数比女生人数少2人,并且每名学生每小时剪筒身50个或剪筒底120个.
(1)七年级(2)班有男生、女生各多少人?
(2)要求一个筒身配两个筒底,为了使每小时剪出的筒身与筒底刚好配套,应该分配多少名学生剪筒身,多少名学生剪筒底?
【分析】(1)设七年级(2)班有女生人,则男生人,根据全班共有44人建立方程求出其解即可;
(2)设分配人生产筒身,人生产筒底,由筒身与筒底的数量关系建立方程求出其解即可.
【解答】解:(1)设七年级(2)班有女生人,则男生人,由题意,得
,
解得:,
男生有:人.
答:七年级(2)班有女生23人,则男生21人;
(2)设分配人生产筒身,人生产筒底,由题意,得
,
解得:.
生产筒底的有20人.
答:分配24人生产筒身,20人生产筒底.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
