初中数学人教版八年级上册11.2.1 三角形的内角 课件 (共18张PPT)
文档属性
| 名称 | 初中数学人教版八年级上册11.2.1 三角形的内角 课件 (共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 320.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-14 15:41:17 | ||
图片预览



文档简介
(共18张PPT)
第十一章 三角形
11.2.1 三角形的内角
八年级数学上册·人教版
想一想
三角形的三个内角和是多少
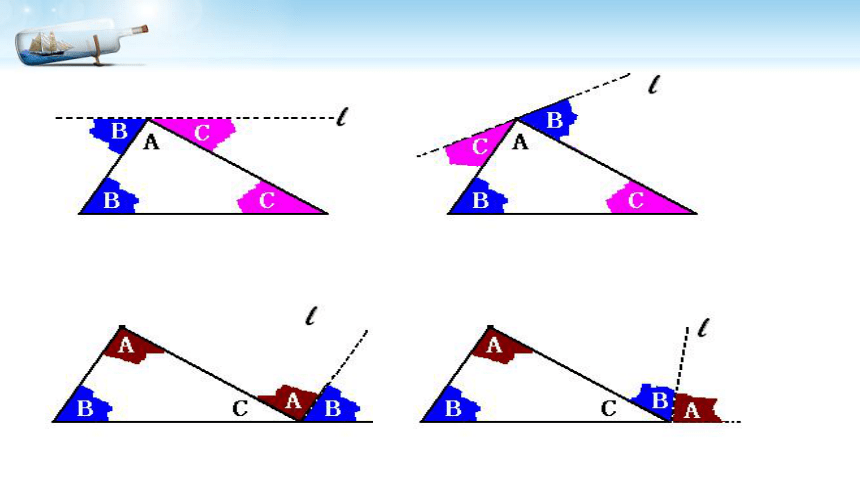
把三个角拼在一起试试看.
有什么办法可以验证呢
三角形的三个内角和等于180°.
结论对任意三角形都成立吗?
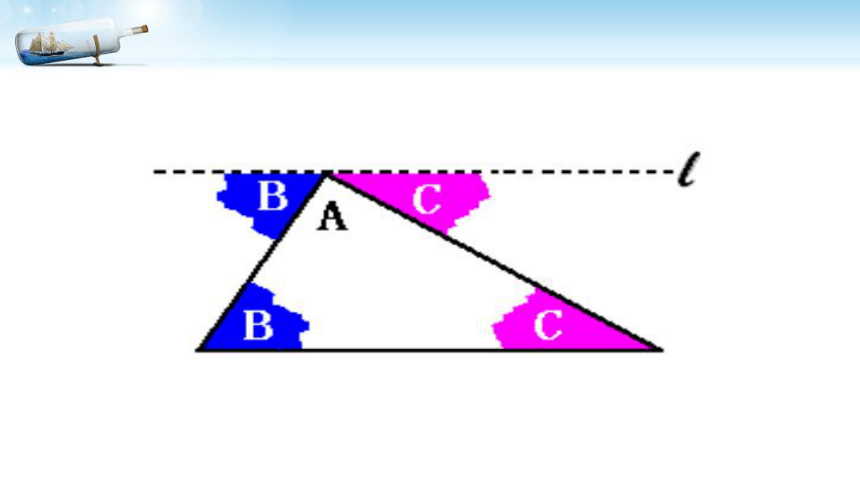
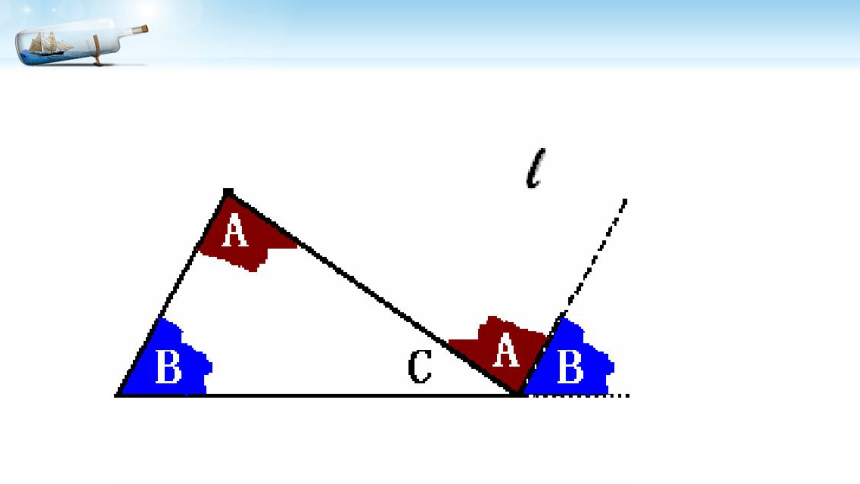
想一想:利用此图该如何说明“三角形的内角和等于180°”?
A
B
C
1
2
3
4
5
l
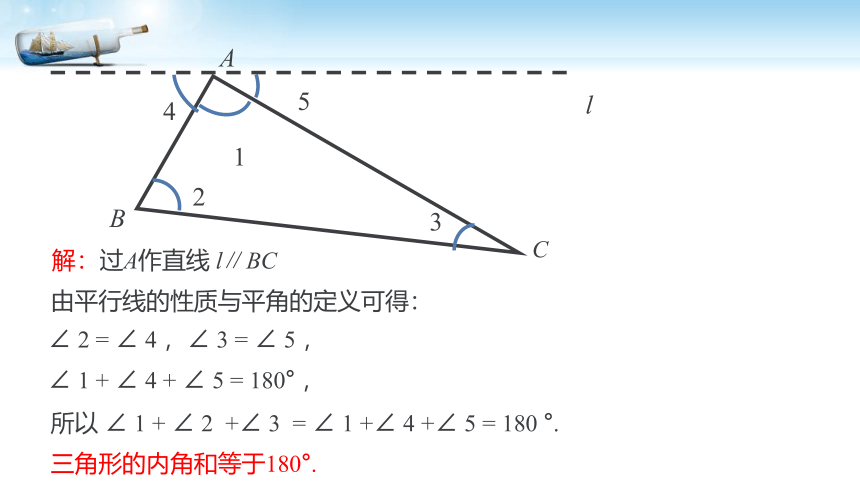
解:过A作直线 l∥BC
由平行线的性质与平角的定义可得:
所以 ∠ 1 + ∠ 2 +∠ 3 = ∠ 1 +∠ 4 +∠ 5 = 180 °.
三角形的内角和等于180°.
∠ 2 = ∠ 4 ,∠ 3 = ∠ 5 ,
∠ 1 + ∠ 4 + ∠ 5 = 180° ,
例:如图,C岛在A岛的北偏东50°的方向,B岛在A岛的北偏东80°的方向,C岛在B岛
的北偏西40°方向.从C岛看A、B两岛的视角∠ACB是多少度?
解:因为∠CAD=50°,∠DAB=80°,
所以∠BAC=∠BAD-∠CAD=30°,
由AD//BE,可得∠DAB+ ∠ ABE =180°,
所以∠ABE=180°-∠DAB= 180°- 80° =100°,
因为∠EBC=40°,
所以∠ABC= ∠ABE- ∠EBC=60°,
所以∠ACB=180°-∠ABC-∠BAC=90°,
答:从C岛看A、B两岛的视角∠ACB是90° .
C岛在A岛的北偏东50°方向,C岛在B岛的北偏西40°方向.从C岛看A、B两岛的视角∠ACB是多少度?
思考题
A
B
C
D
北
E
北
50°
40°
如果不用“三角形的的内角和等于180 ”,你能解决这道题吗?
F
检验一下自己吧!
(口答)下列各组角是同一个三角形的内角吗?
为什么?
(1)3°, 150°, 27°;
(2)60°, 40°, 90°;
(3)30°, 60°, 50°.
(是 )
( 不是)
( 不是)
80°
X°
X°
你能求出图中X的值吗
X=50
1. 在△ABC中,∠A=80°,∠B=∠C , 求∠C的度数.
解:在△ABC中,∠A+∠B+∠C=180°,∠A=80°,
∴∠B+∠C=100°,
∵∠B=∠C,
∴∠B=∠C=500.
2.已知三角形三个内角的度数之比为1:3:5,求这三个内角的度数.
解:设三个内角度数分别为:x、3x、5x,
列出方程 x+3x+5x=180,
x=20,
答:三个内角度数分别20°,60°,100°.
3. 如图,一种滑翔伞是左右对称的四边形ABCD,其中∠A=150°,
∠B=∠D=40°.求∠C的度数.
D
40 °
40 °
150°
A
B
C
1
2
解:在△ABC中 ∠B+∠1+∠BAC=180°,
在△ACD中 ∠D+∠2+∠DAC=180°,
∴∠B+∠D+∠1+∠2+∠BAC+∠CAD=360 °,
即 ∠B+∠D+ ∠BCD +∠BAD= 360 °,
40 °+40 °+ ∠BCD +150 ° = 360 °,
∴ ∠BCD = 360 °-40 °- 40 °- 150 °=130 °.
如图,若AB∥CD,则∠1、∠2与∠C、∠D之间有什么数量关系?为什么?
如图,若AB不平行于CD,则∠1、∠2与∠C、∠D之间的这些关系还成立吗?为什么?
如图,若A、B分别在DO、CO的延长线上,则∠1、∠2与∠C、∠D之间的关系还成立吗?为什么?
∠1=∠C,∠2=∠D
∠1+∠2=∠C+∠D
∠1+∠2=∠C+∠D
∠1+∠2=∠C+∠D
O
A
B
C
D
1
S
O
A
B
C
D
1
2
O
A
B
C
D
1
2
课堂小结
通过本堂课的学习,你有哪些收获?
作业:
1.任选一种方法说理:三角形的内角和是180。.
2.P16. 3、 4题.
本课结束
第十一章 三角形
11.2.1 三角形的内角
八年级数学上册·人教版
想一想
三角形的三个内角和是多少
把三个角拼在一起试试看.
有什么办法可以验证呢
三角形的三个内角和等于180°.
结论对任意三角形都成立吗?
想一想:利用此图该如何说明“三角形的内角和等于180°”?
A
B
C
1
2
3
4
5
l
解:过A作直线 l∥BC
由平行线的性质与平角的定义可得:
所以 ∠ 1 + ∠ 2 +∠ 3 = ∠ 1 +∠ 4 +∠ 5 = 180 °.
三角形的内角和等于180°.
∠ 2 = ∠ 4 ,∠ 3 = ∠ 5 ,
∠ 1 + ∠ 4 + ∠ 5 = 180° ,
例:如图,C岛在A岛的北偏东50°的方向,B岛在A岛的北偏东80°的方向,C岛在B岛
的北偏西40°方向.从C岛看A、B两岛的视角∠ACB是多少度?
解:因为∠CAD=50°,∠DAB=80°,
所以∠BAC=∠BAD-∠CAD=30°,
由AD//BE,可得∠DAB+ ∠ ABE =180°,
所以∠ABE=180°-∠DAB= 180°- 80° =100°,
因为∠EBC=40°,
所以∠ABC= ∠ABE- ∠EBC=60°,
所以∠ACB=180°-∠ABC-∠BAC=90°,
答:从C岛看A、B两岛的视角∠ACB是90° .
C岛在A岛的北偏东50°方向,C岛在B岛的北偏西40°方向.从C岛看A、B两岛的视角∠ACB是多少度?
思考题
A
B
C
D
北
E
北
50°
40°
如果不用“三角形的的内角和等于180 ”,你能解决这道题吗?
F
检验一下自己吧!
(口答)下列各组角是同一个三角形的内角吗?
为什么?
(1)3°, 150°, 27°;
(2)60°, 40°, 90°;
(3)30°, 60°, 50°.
(是 )
( 不是)
( 不是)
80°
X°
X°
你能求出图中X的值吗
X=50
1. 在△ABC中,∠A=80°,∠B=∠C , 求∠C的度数.
解:在△ABC中,∠A+∠B+∠C=180°,∠A=80°,
∴∠B+∠C=100°,
∵∠B=∠C,
∴∠B=∠C=500.
2.已知三角形三个内角的度数之比为1:3:5,求这三个内角的度数.
解:设三个内角度数分别为:x、3x、5x,
列出方程 x+3x+5x=180,
x=20,
答:三个内角度数分别20°,60°,100°.
3. 如图,一种滑翔伞是左右对称的四边形ABCD,其中∠A=150°,
∠B=∠D=40°.求∠C的度数.
D
40 °
40 °
150°
A
B
C
1
2
解:在△ABC中 ∠B+∠1+∠BAC=180°,
在△ACD中 ∠D+∠2+∠DAC=180°,
∴∠B+∠D+∠1+∠2+∠BAC+∠CAD=360 °,
即 ∠B+∠D+ ∠BCD +∠BAD= 360 °,
40 °+40 °+ ∠BCD +150 ° = 360 °,
∴ ∠BCD = 360 °-40 °- 40 °- 150 °=130 °.
如图,若AB∥CD,则∠1、∠2与∠C、∠D之间有什么数量关系?为什么?
如图,若AB不平行于CD,则∠1、∠2与∠C、∠D之间的这些关系还成立吗?为什么?
如图,若A、B分别在DO、CO的延长线上,则∠1、∠2与∠C、∠D之间的关系还成立吗?为什么?
∠1=∠C,∠2=∠D
∠1+∠2=∠C+∠D
∠1+∠2=∠C+∠D
∠1+∠2=∠C+∠D
O
A
B
C
D
1
S
O
A
B
C
D
1
2
O
A
B
C
D
1
2
课堂小结
通过本堂课的学习,你有哪些收获?
作业:
1.任选一种方法说理:三角形的内角和是180。.
2.P16. 3、 4题.
本课结束
