初中数学人教版八年级上册 1.1.1三角形的边 课件(共28张PPT)
文档属性
| 名称 | 初中数学人教版八年级上册 1.1.1三角形的边 课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-14 15:43:39 | ||
图片预览






文档简介
(共28张PPT)
第十一章 三角形
11.1.1 三角形的边
八年级数学上册·人教版
学习目标
1.了解三角形的概念,认识三角形的边、顶点、内角,会用符号
语言表示三角形.
2.会把三角形按边或角进行分类,进一步了解分类思想.
3.掌握三角形三边的不等关系,并能运用它解决生活中实际问题.
学习重点、难点
运用三角形的三边关系判断三条线段能否组成三角形.
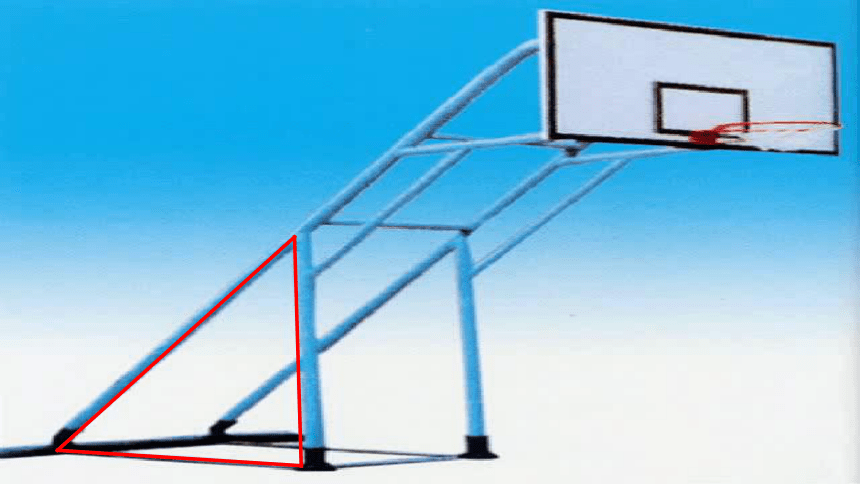
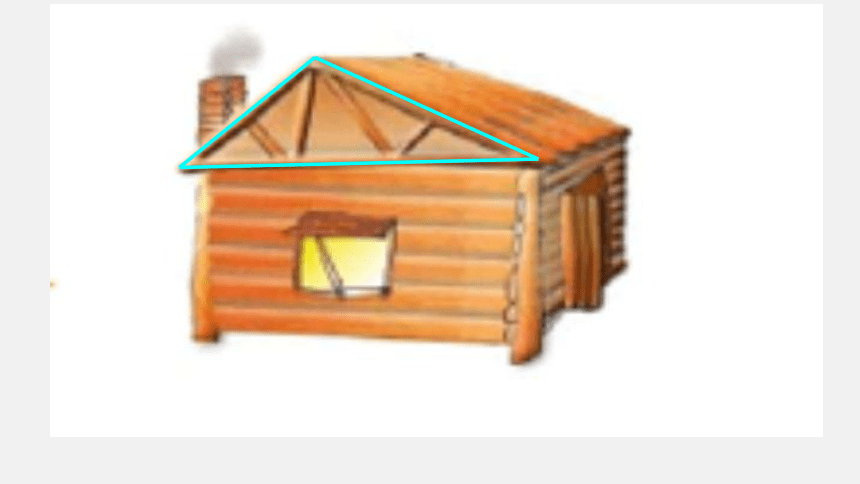
你能画一个三角形吗?
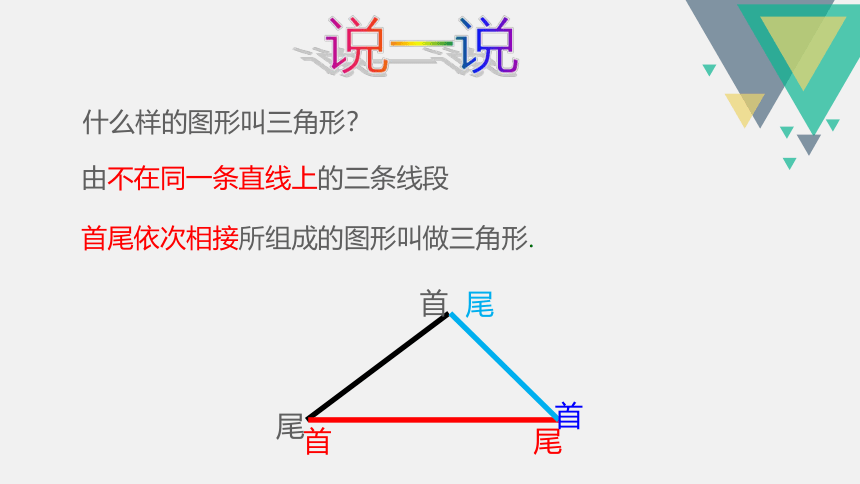
说一说
什么样的图形叫三角形?
首
尾
首
尾
首
尾
由不在同一条直线上的三条线段
首尾依次相接所组成的图形叫做三角形.
自学教科书第2、3页的内容,并思考下面问题:
1.知道三角形的顶点,角,边等概念,会用几何符号表示一个三角形;
2.会把三角形进行分类,知道每类三角形的特征;
3.知道等腰三角形的腰,底边,顶角,底角等概念;
A
B
C
记作:△ABC读作:三角形ABC.
三角形的顶点:A、 B、 C.
三角形的边:AB、AC、BC
c
c
b
b
a
a
三角形的内角: A、 B、 C.
三角形
按角分
锐角三角形
直角三角形
钝角三角形
按边分
不等边三角形
三角形的分类
等腰三角形
腰≠底的三角形
等边三角形
不等边三角形
等腰三角形
等边三角形
腰
腰
底
顶角
底角
底角
等腰三角形的构成
1.如图是用三根细棍组成的图形, 其中符合三角形概念的图形是( )
D.
A.
C.
B.
D
练一练:
A
B
C
D
ΔABD.
ΔBCD,
【答案】ΔABC,
2.图中有几个三角形 请聪明的你用符号表示出来这些三角形.
3.如图,回答下列问题:
(1)图中有____个三角形;
(2)∠1是哪个三角形的角?
(3)以CE为一条边的三角形有几个?分别是?
8
答案:△BDO 和△ BDC.
答案:两个:△BCE 和△COE.
B
C
A
D
E
O
1
自己动手试一试
有这样的四根小棒(4cm、6cm、10cm、12cm)请你任意的取其中的三根,首尾连接,摆成三角形.
解:1.(1)4cm、6cm、10cm;
(2)4cm、6cm、12cm;
(3)4cm、10cm、12cm;(4)6cm、10cm、12cm;
2.经过实践可知:
(1)(2)不可以摆出三角形;(3)(4)可以摆出三角形.
1.有哪几种取法
2.是不是任意三根都能摆出三角形?若不是,哪些可以?哪些不可以?
3.用三根什么样的小棒才能拼成三角形呢 你从中发现了什么?
你发现了吗?
这就是说:
三角形中两边的和大于第三边.
我们可以发现这四根小棒中,如果较短的两根的和不大于最长的第三根,就不能组成三角形.
三角形中任意两边的差与第三边有什么关系 你能根据上面的结论,利用不等式的性质加以说明吗
>
>
>
a
c
b
a +b
c
b+ c
a
a +c
b
A
B
C
a > c – b, b >c - a
b > a – c, c>a- b
a > b – c, c>b - a
三角形两边的差小于第三边.
例:等腰三角形的周长为18cm
(1)如果腰长是底边长的2倍,求各边的长;
(2)如果一边长为4cm,求另两边的长.
解:(1)设等腰三角形的底边长为xcm,
则腰长为2xcm,根据题意,得
x+2x+2x=18,
解方程,得
x=3.6.
例题解析,再探新知
解:(2)若底边长为4cm,设腰长为xcm,则有
2x+4=18,
解方程,得
x=7,
若一条腰长为4cm,设底边长为xcm,则有
2×4+x=18,
x=10,
解方程,得
因为4+4<10,所以4cm为一腰不能构成三角形,
所以,三角形的另两边长都是7cm.
例题解析,再探新知
下列长度的三条线段能否组成三角形?为什么?
(1) 8,4,3 ( )
(2) 6,2,5 ( )
(3) 5,6,10 ( )
(4) 5,8,3 ( )
不能
能
能
不能
判断三条线段能否组成三角形,是否一定要检验三条线段中任何两条的和都大于第三条?根据你刚才解题经验,有没有更简便的判断方法?
思 考:
答案:只要满足较小的两条线段之和大于第三条线段,
便可构成三角形;若不满足,则不能构成三角形.
练一练
答:不能.如果此人一步能走3米,由三角形三边的关系得,此人两腿长之和要大于3米,这与实际情况相矛盾,所以它一步不能走3米.
姚明腿长1.28米.
考考你
有人说他一步能走3米,你相信吗?
能否用今天学过的知识去解答呢
请用所学的数学知识解释:
2.两点之间的所有连线中,线段最短.
1.三角形任意两边之和大于第三边.
人行横道
.A
.B
为什么经常有行人斜穿马路而不走人行横道
1.有长为3、5、7、10四根木条,要摆出一个三角形,有___种摆法
2
2.一个等腰三角形的一边是2cm,另一边是9cm,则这个三角形的周长是______.
20cm
3. 一个等腰三角形的一边是5cm,另一边是9cm,则这个三角形的周长是______________.
19cm或23cm
1.通过这节课的学习你有什么收获?
2.你还有什么疑问和不懂的地方吗?
感悟与反思
要学会学习!
草原上有四口油井,位于如图所示的A、B、C、D四个位置,现在要建立一个维修站H,问H建在何处,才能使它到四个油井的距离之和HA+HB+HC+HD为最小?说明理由.
A
D
C
B
H
H′
提示:到A、C距离和最小的点在哪儿?到B、D
看谁最聪明!
本课结束
第十一章 三角形
11.1.1 三角形的边
八年级数学上册·人教版
学习目标
1.了解三角形的概念,认识三角形的边、顶点、内角,会用符号
语言表示三角形.
2.会把三角形按边或角进行分类,进一步了解分类思想.
3.掌握三角形三边的不等关系,并能运用它解决生活中实际问题.
学习重点、难点
运用三角形的三边关系判断三条线段能否组成三角形.
你能画一个三角形吗?
说一说
什么样的图形叫三角形?
首
尾
首
尾
首
尾
由不在同一条直线上的三条线段
首尾依次相接所组成的图形叫做三角形.
自学教科书第2、3页的内容,并思考下面问题:
1.知道三角形的顶点,角,边等概念,会用几何符号表示一个三角形;
2.会把三角形进行分类,知道每类三角形的特征;
3.知道等腰三角形的腰,底边,顶角,底角等概念;
A
B
C
记作:△ABC读作:三角形ABC.
三角形的顶点:A、 B、 C.
三角形的边:AB、AC、BC
c
c
b
b
a
a
三角形的内角: A、 B、 C.
三角形
按角分
锐角三角形
直角三角形
钝角三角形
按边分
不等边三角形
三角形的分类
等腰三角形
腰≠底的三角形
等边三角形
不等边三角形
等腰三角形
等边三角形
腰
腰
底
顶角
底角
底角
等腰三角形的构成
1.如图是用三根细棍组成的图形, 其中符合三角形概念的图形是( )
D.
A.
C.
B.
D
练一练:
A
B
C
D
ΔABD.
ΔBCD,
【答案】ΔABC,
2.图中有几个三角形 请聪明的你用符号表示出来这些三角形.
3.如图,回答下列问题:
(1)图中有____个三角形;
(2)∠1是哪个三角形的角?
(3)以CE为一条边的三角形有几个?分别是?
8
答案:△BDO 和△ BDC.
答案:两个:△BCE 和△COE.
B
C
A
D
E
O
1
自己动手试一试
有这样的四根小棒(4cm、6cm、10cm、12cm)请你任意的取其中的三根,首尾连接,摆成三角形.
解:1.(1)4cm、6cm、10cm;
(2)4cm、6cm、12cm;
(3)4cm、10cm、12cm;(4)6cm、10cm、12cm;
2.经过实践可知:
(1)(2)不可以摆出三角形;(3)(4)可以摆出三角形.
1.有哪几种取法
2.是不是任意三根都能摆出三角形?若不是,哪些可以?哪些不可以?
3.用三根什么样的小棒才能拼成三角形呢 你从中发现了什么?
你发现了吗?
这就是说:
三角形中两边的和大于第三边.
我们可以发现这四根小棒中,如果较短的两根的和不大于最长的第三根,就不能组成三角形.
三角形中任意两边的差与第三边有什么关系 你能根据上面的结论,利用不等式的性质加以说明吗
>
>
>
a
c
b
a +b
c
b+ c
a
a +c
b
A
B
C
a > c – b, b >c - a
b > a – c, c>a- b
a > b – c, c>b - a
三角形两边的差小于第三边.
例:等腰三角形的周长为18cm
(1)如果腰长是底边长的2倍,求各边的长;
(2)如果一边长为4cm,求另两边的长.
解:(1)设等腰三角形的底边长为xcm,
则腰长为2xcm,根据题意,得
x+2x+2x=18,
解方程,得
x=3.6.
例题解析,再探新知
解:(2)若底边长为4cm,设腰长为xcm,则有
2x+4=18,
解方程,得
x=7,
若一条腰长为4cm,设底边长为xcm,则有
2×4+x=18,
x=10,
解方程,得
因为4+4<10,所以4cm为一腰不能构成三角形,
所以,三角形的另两边长都是7cm.
例题解析,再探新知
下列长度的三条线段能否组成三角形?为什么?
(1) 8,4,3 ( )
(2) 6,2,5 ( )
(3) 5,6,10 ( )
(4) 5,8,3 ( )
不能
能
能
不能
判断三条线段能否组成三角形,是否一定要检验三条线段中任何两条的和都大于第三条?根据你刚才解题经验,有没有更简便的判断方法?
思 考:
答案:只要满足较小的两条线段之和大于第三条线段,
便可构成三角形;若不满足,则不能构成三角形.
练一练
答:不能.如果此人一步能走3米,由三角形三边的关系得,此人两腿长之和要大于3米,这与实际情况相矛盾,所以它一步不能走3米.
姚明腿长1.28米.
考考你
有人说他一步能走3米,你相信吗?
能否用今天学过的知识去解答呢
请用所学的数学知识解释:
2.两点之间的所有连线中,线段最短.
1.三角形任意两边之和大于第三边.
人行横道
.A
.B
为什么经常有行人斜穿马路而不走人行横道
1.有长为3、5、7、10四根木条,要摆出一个三角形,有___种摆法
2
2.一个等腰三角形的一边是2cm,另一边是9cm,则这个三角形的周长是______.
20cm
3. 一个等腰三角形的一边是5cm,另一边是9cm,则这个三角形的周长是______________.
19cm或23cm
1.通过这节课的学习你有什么收获?
2.你还有什么疑问和不懂的地方吗?
感悟与反思
要学会学习!
草原上有四口油井,位于如图所示的A、B、C、D四个位置,现在要建立一个维修站H,问H建在何处,才能使它到四个油井的距离之和HA+HB+HC+HD为最小?说明理由.
A
D
C
B
H
H′
提示:到A、C距离和最小的点在哪儿?到B、D
看谁最聪明!
本课结束
