暑假自学专题:角的度量(综合训练)-数学四年级上册人教版(含答案)
文档属性
| 名称 | 暑假自学专题:角的度量(综合训练)-数学四年级上册人教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-15 15:40:44 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
暑假自学专题:角的度量(综合训练)-数学四年级上册人教版
一、选择题
1.过两点可以画( )条直线。
A.1 B.2 C.无数
2.直线与射线比较,( )。
A.直线更长 B.射线更长 C.无法比较
3.角的两条边是两条( )。
A.射线 B.线段 C.直线
4.笑笑用量角器量角的度数时,误把外圈刻度看成内圈刻度,读得角的度数是140°,那么这个角的正确度数是( )。
A.140° B.40° C.50°
5.在连接A、B两点的线中,( )最短。
A.第①条 B.第②条 C.第③条
6.从6:00到9:00,时针旋转了( )度。
A.90° B.180° C.360° D.120°
二、填空题
7.钟面上( )时整,时针和分针正好成平角。
8.已知,那么( ),( ),( )。
9.∠1+直角+35°=平角,则∠1=( )。
10.下图中共有( )条射线。
11.小于90°的角是( )角,等于90°的角是( )角,大于90°而小于180°的角是( )角。
12.使用量角器测量角的度数时,量角器的中心要与角的( )重合,( )°刻度线与角的一边重合。
三、判断题
13.角的大小与角的两条边的长短无关。( )
14.从一个端点可以画无数条射线。( )
15.将一个平角分成两个角,可以得到一个锐角和一个直角。( )
16.一条直线长10米。( )
17.在电视屏幕上将角放大,角的度数也变大了。( )
四、解答题
18.如下图所示,∠1=55°,请你求出。∠2,∠3,∠4的度数。
19.用量角器画一个110°的角,并指出它是哪一种角。
20.如下图,已知∠2是∠1的3倍,请你算一算∠1、∠2、∠3和∠4的度数分别是多少?
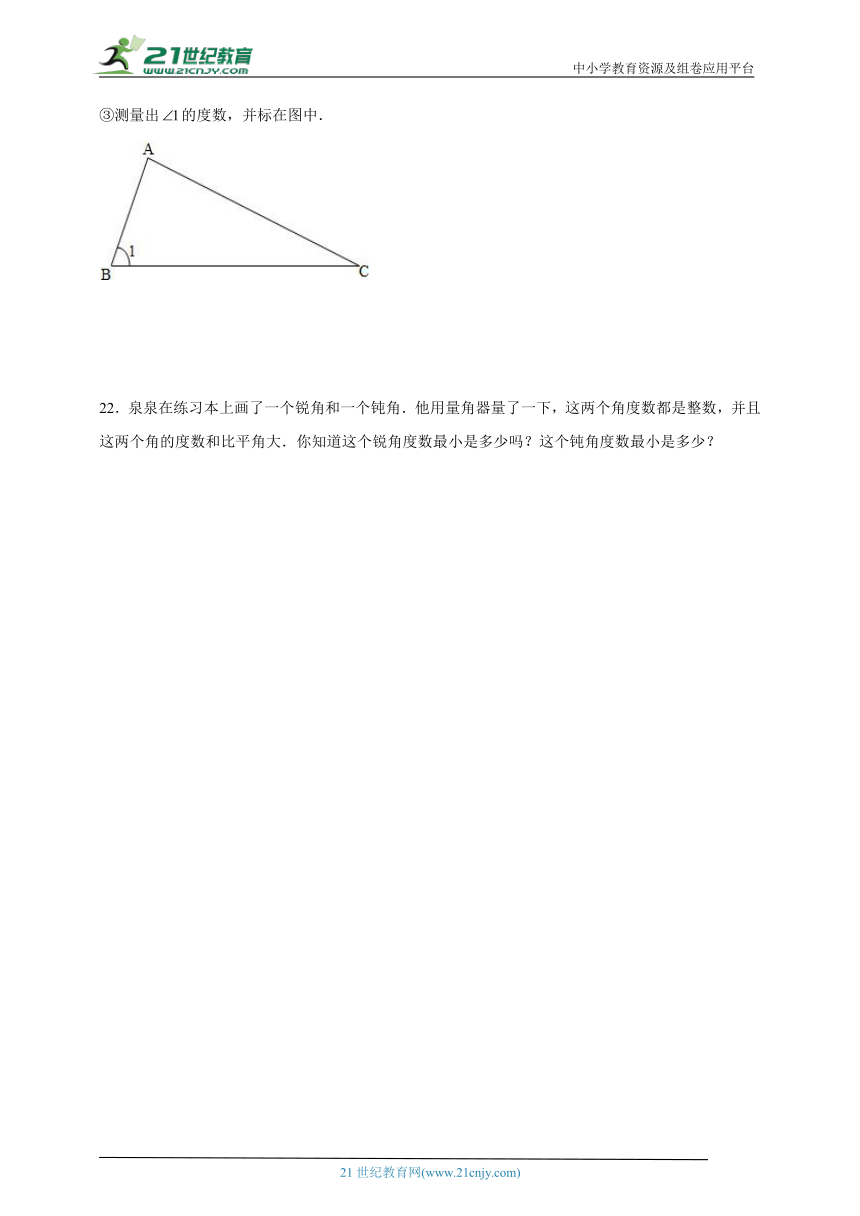
21.有一块三角形地(如图).
①从点走到对边,怎样走最近?在图上画出来.
②过点作边的平行线.
③测量出的度数,并标在图中.
22.泉泉在练习本上画了一个锐角和一个钝角.他用量角器量了一下,这两个角度数都是整数,并且这两个角的度数和比平角大.你知道这个锐角度数最小是多少吗?这个钝角度数最小是多少?
参考答案:
1.A
【分析】把线段向两端无限延伸,就得到一条直线,直线没有端点,是无限长的,依此画图并选择即可。
【详解】根据分析,画图如下:
由此可知,过两点可以画1条直线。
故答案为:A
【点睛】熟练掌握直线的特点是解答此题的关键。
2.C
【分析】把线段的两端无限延长,得到一条直线,直线没有端点,无限长。把线段的一端无限延长,得到一条射线,射线有一个端点,无限长。则直线和射线的长度不能比较大小,据此判断即可。
【详解】因为直线和射线都是无限长的,不能度量,也就无法比较。
故答案为:C
【点睛】本题考查直线和射线的性质,直线和射线无限长,而线段是有限长的,两条线段的长度可以比较大小。
3.A
【分析】从一点引出两条射线所组成的图形叫做角,依此选择。
【详解】根据分析可知,角的两条边是两条射线(如图所示)。
故答案为:A
【点睛】熟练掌握角的特点是解答此题的关键。
4.B
【分析】根据量角器的构造即可求解,注意外圈刻度与内圈刻度的和是180°,误把外圈刻度当成了内圈刻度,读得度数是140°,正确的度数是(180-140)°;由此选择即可。
【详解】180°-140°=40°
这个角的正确度数是40°。
故答案为:B
【点睛】熟练掌握量角器量角的方法是解答本题的关键。
5.B
【分析】根据两点之间线段最短进行解答即可。
【详解】一根拉紧的线,绷紧的弦,都可以看作线段,线段有两个端点,因此第②条最短。
故答案为:B
【点睛】本题考查的是两点之间线段最短,应熟练掌握。
6.A
【分析】钟面上12个数字把钟面平均分成12份,每份所对应的圆周角是360°÷12=30°,即每两个相邻数字间的圆心角是30°,时针从6:00到9:00顺时针走过了三个数字,即走过了3个30°,据此即可解答。
【详解】由分析得,
时针从6:00到9:00按顺时针方向,旋转了30×3=90(度)
故选:A
【点睛】此题考查旋转及钟面的认识,解答此题关键掌握在钟面上指针每走一个数字,绕中心轴旋转30°。
7.6
【分析】钟面上12个数字把钟面平均分成12个大格,每个大格的度数是30度,6整时,分针指向12,当时针指向6时,夹角是180度,即为平角,由此进行解答即可。
【详解】据分析可得:钟面上(6)时整,时针和分针正好成平角。
【点睛】本题考查钟表时针与分针的夹角。在钟表问题中,要知道钟表12个数字,每相邻两个数字之间的夹角为30度。
8.
【分析】根据图意知:和,、组成了平角,、组成了平角,据此解答即可。
【详解】
所以,,。
【点睛】解决本题的关键是利用各个角与特殊角平角的关系解答。
9.55度/55
【分析】平角等于180°,直角为90°,代入数据计算即可。
【详解】∠1+直角+35°=平角,
即∠1+90°+35°=180°,
所以∠1=180°-90°-35°,
故∠1=55°。
【点睛】解决本题的关键是明确直角和平角的度数。
10.8
【分析】射线只有一个端点,可以向一端无限延伸,所以图中每个端点都可以看作是射线的一个端点,从一个端点向左、向右可以分别得到2条射线,据此解答即可。
【详解】根据分析可得,图中共有4个端点,每个端点可以得到2条射线,所以该图一共可以得到的射线条数为:4×2=8(条)。
【点睛】本题考查的是对射线特征的理解掌握。
11. 锐 直 钝
【分析】根据锐角、直角和钝角的定义解答。
【详解】小于90°的角是锐角,等于90°的角是直角,大于90°而小于180°的角是钝角。
【点睛】本题考查角的分类,熟练掌握锐角、直角和钝角的定义是解决本题的关键。
12. 顶点 0
【详解】量角的步骤是:先把量角器的中心与角的顶点重合,0°刻度线与角的一条边重合,角的另一边所对的量角器上的刻度,就是这个角的度数。如图所示:
13.√
【分析】由一点引出的两条射线组成的图形叫做角,角的大小与边的长短无关,与两边叉开的大小有关,叉开越大角就越大,反之越小;据此即可解答。
【详解】根据分析可知,角的大小与边的长短没有关系,只与角的两条边叉开的大小有关系,原说法正确。
故答案为:√
【点睛】本题主要考查学生对影响角的大小因素的掌握和灵活运用。
14.√
【分析】根据射线的定义及特点可知:射线有一个端点,无限长,从一点出发可以作无数条射线;据此解答。
【详解】由分析可知:过一点可以画无数条射线,原说法正确。
故答案为:√
【点睛】此题主要考查射线的定义及特点。
15.×
【分析】根据平角=180°,0°<锐角<90°,直角=90°,90°<钝角<180°,180°-锐角所得的角的度数大于90°,据此解答。
【详解】把一个平角分成两个角,可能分成一个锐角和一个钝角;
故答案为:×。
【点睛】本题考查角的分类,关键灵活应用锐角、直角、钝角的知识。
16.×
【分析】根据直线、线段和射线的特点:直线没有端点,无限长,不可以度量;射线只有一个端点,向一方无限延长,不可以度量;线段有两个端点,有限长,可以度量;据此判断。
【详解】直线没有端点,无限长,不可以度量,所以一条直线长10米,此说法错误。
故答案为:×
【点睛】此题考查了线段、射线和直线的含义,应灵活运用。
17.×
【分析】电视屏幕只会放大角两边的长度,不会改变角的度数,依此判断即可。
【详解】在电视屏幕上将角放大,角的度数没有改变。
故答案为:×
【点睛】熟练掌握电视屏幕放大角的特点是解答此题的关键。
18.∠2=125°;∠3=55°;∠4=35°
【分析】根据图意可知∠1和∠2组成了平角,∠2和∠3组成了平角,∠1和∠4组成了直角;据此解答。
【详解】∠4=90°-∠1
=90°-55°
=35°
∠2=180°-∠1
=180°-55°
=125°
∠3=180°-∠2
=180°-125°
=55°
答:∠2=125°;∠3=55°;∠4=35°。
【点睛】解答本题的关键是从∠1入手看哪几个角组成的是直角和平角,再进行计算。
19.;钝角。
【分析】画一条射线,使量角器的中心和射线的端点重合,0°刻度线和射线重合。在量角器110°刻度线的地方点一个点。以画出的射线的端点为端点,通过刚画的点,再画一条射线。据此画出110°的角。大于90°小于180°的角叫钝角,则110°的角是钝角。
【详解】用量角器画一个110°的角,如图所示:
根据钝角的定义可知,它是钝角。
答:它是钝角。
【点睛】熟练掌握角的画法和钝角的定义,注意平时基础知识的积累。
20.∠1=45° ∠2=135° ∠3=45° ∠4=135°
【解析】略
21.如图所示:
①从点走到对边,沿走最近;
②过点作出边的平行线,如图:
③测量出的度数为;
【详解】①根据从直线外一点到这条直线的所有连线中,垂线段最短;由此过点向作垂线,交于点;
②三角板的一条直角边与已知直线重合,用直尺靠紧三角板的另一条直角边,沿直尺移动三角板,使三角板和已知直线重合的直角边和点重合,过点沿三角板的直角边画直线即可;
③用量角器的刻度线对准所量角的一条边,用中心点对准顶点,看看另一条边在哪一刻度这个角就是几度.
22.锐角最小为2°钝角最小为92°
【详解】因为都是整度数,所以最大钝角为179°,大于平角的最小度数为181°,由此得出:181°-179°=2° 钝角最小为92° 181°-89°=92°
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
暑假自学专题:角的度量(综合训练)-数学四年级上册人教版
一、选择题
1.过两点可以画( )条直线。
A.1 B.2 C.无数
2.直线与射线比较,( )。
A.直线更长 B.射线更长 C.无法比较
3.角的两条边是两条( )。
A.射线 B.线段 C.直线
4.笑笑用量角器量角的度数时,误把外圈刻度看成内圈刻度,读得角的度数是140°,那么这个角的正确度数是( )。
A.140° B.40° C.50°
5.在连接A、B两点的线中,( )最短。
A.第①条 B.第②条 C.第③条
6.从6:00到9:00,时针旋转了( )度。
A.90° B.180° C.360° D.120°
二、填空题
7.钟面上( )时整,时针和分针正好成平角。
8.已知,那么( ),( ),( )。
9.∠1+直角+35°=平角,则∠1=( )。
10.下图中共有( )条射线。
11.小于90°的角是( )角,等于90°的角是( )角,大于90°而小于180°的角是( )角。
12.使用量角器测量角的度数时,量角器的中心要与角的( )重合,( )°刻度线与角的一边重合。
三、判断题
13.角的大小与角的两条边的长短无关。( )
14.从一个端点可以画无数条射线。( )
15.将一个平角分成两个角,可以得到一个锐角和一个直角。( )
16.一条直线长10米。( )
17.在电视屏幕上将角放大,角的度数也变大了。( )
四、解答题
18.如下图所示,∠1=55°,请你求出。∠2,∠3,∠4的度数。
19.用量角器画一个110°的角,并指出它是哪一种角。
20.如下图,已知∠2是∠1的3倍,请你算一算∠1、∠2、∠3和∠4的度数分别是多少?
21.有一块三角形地(如图).
①从点走到对边,怎样走最近?在图上画出来.
②过点作边的平行线.
③测量出的度数,并标在图中.
22.泉泉在练习本上画了一个锐角和一个钝角.他用量角器量了一下,这两个角度数都是整数,并且这两个角的度数和比平角大.你知道这个锐角度数最小是多少吗?这个钝角度数最小是多少?
参考答案:
1.A
【分析】把线段向两端无限延伸,就得到一条直线,直线没有端点,是无限长的,依此画图并选择即可。
【详解】根据分析,画图如下:
由此可知,过两点可以画1条直线。
故答案为:A
【点睛】熟练掌握直线的特点是解答此题的关键。
2.C
【分析】把线段的两端无限延长,得到一条直线,直线没有端点,无限长。把线段的一端无限延长,得到一条射线,射线有一个端点,无限长。则直线和射线的长度不能比较大小,据此判断即可。
【详解】因为直线和射线都是无限长的,不能度量,也就无法比较。
故答案为:C
【点睛】本题考查直线和射线的性质,直线和射线无限长,而线段是有限长的,两条线段的长度可以比较大小。
3.A
【分析】从一点引出两条射线所组成的图形叫做角,依此选择。
【详解】根据分析可知,角的两条边是两条射线(如图所示)。
故答案为:A
【点睛】熟练掌握角的特点是解答此题的关键。
4.B
【分析】根据量角器的构造即可求解,注意外圈刻度与内圈刻度的和是180°,误把外圈刻度当成了内圈刻度,读得度数是140°,正确的度数是(180-140)°;由此选择即可。
【详解】180°-140°=40°
这个角的正确度数是40°。
故答案为:B
【点睛】熟练掌握量角器量角的方法是解答本题的关键。
5.B
【分析】根据两点之间线段最短进行解答即可。
【详解】一根拉紧的线,绷紧的弦,都可以看作线段,线段有两个端点,因此第②条最短。
故答案为:B
【点睛】本题考查的是两点之间线段最短,应熟练掌握。
6.A
【分析】钟面上12个数字把钟面平均分成12份,每份所对应的圆周角是360°÷12=30°,即每两个相邻数字间的圆心角是30°,时针从6:00到9:00顺时针走过了三个数字,即走过了3个30°,据此即可解答。
【详解】由分析得,
时针从6:00到9:00按顺时针方向,旋转了30×3=90(度)
故选:A
【点睛】此题考查旋转及钟面的认识,解答此题关键掌握在钟面上指针每走一个数字,绕中心轴旋转30°。
7.6
【分析】钟面上12个数字把钟面平均分成12个大格,每个大格的度数是30度,6整时,分针指向12,当时针指向6时,夹角是180度,即为平角,由此进行解答即可。
【详解】据分析可得:钟面上(6)时整,时针和分针正好成平角。
【点睛】本题考查钟表时针与分针的夹角。在钟表问题中,要知道钟表12个数字,每相邻两个数字之间的夹角为30度。
8.
【分析】根据图意知:和,、组成了平角,、组成了平角,据此解答即可。
【详解】
所以,,。
【点睛】解决本题的关键是利用各个角与特殊角平角的关系解答。
9.55度/55
【分析】平角等于180°,直角为90°,代入数据计算即可。
【详解】∠1+直角+35°=平角,
即∠1+90°+35°=180°,
所以∠1=180°-90°-35°,
故∠1=55°。
【点睛】解决本题的关键是明确直角和平角的度数。
10.8
【分析】射线只有一个端点,可以向一端无限延伸,所以图中每个端点都可以看作是射线的一个端点,从一个端点向左、向右可以分别得到2条射线,据此解答即可。
【详解】根据分析可得,图中共有4个端点,每个端点可以得到2条射线,所以该图一共可以得到的射线条数为:4×2=8(条)。
【点睛】本题考查的是对射线特征的理解掌握。
11. 锐 直 钝
【分析】根据锐角、直角和钝角的定义解答。
【详解】小于90°的角是锐角,等于90°的角是直角,大于90°而小于180°的角是钝角。
【点睛】本题考查角的分类,熟练掌握锐角、直角和钝角的定义是解决本题的关键。
12. 顶点 0
【详解】量角的步骤是:先把量角器的中心与角的顶点重合,0°刻度线与角的一条边重合,角的另一边所对的量角器上的刻度,就是这个角的度数。如图所示:
13.√
【分析】由一点引出的两条射线组成的图形叫做角,角的大小与边的长短无关,与两边叉开的大小有关,叉开越大角就越大,反之越小;据此即可解答。
【详解】根据分析可知,角的大小与边的长短没有关系,只与角的两条边叉开的大小有关系,原说法正确。
故答案为:√
【点睛】本题主要考查学生对影响角的大小因素的掌握和灵活运用。
14.√
【分析】根据射线的定义及特点可知:射线有一个端点,无限长,从一点出发可以作无数条射线;据此解答。
【详解】由分析可知:过一点可以画无数条射线,原说法正确。
故答案为:√
【点睛】此题主要考查射线的定义及特点。
15.×
【分析】根据平角=180°,0°<锐角<90°,直角=90°,90°<钝角<180°,180°-锐角所得的角的度数大于90°,据此解答。
【详解】把一个平角分成两个角,可能分成一个锐角和一个钝角;
故答案为:×。
【点睛】本题考查角的分类,关键灵活应用锐角、直角、钝角的知识。
16.×
【分析】根据直线、线段和射线的特点:直线没有端点,无限长,不可以度量;射线只有一个端点,向一方无限延长,不可以度量;线段有两个端点,有限长,可以度量;据此判断。
【详解】直线没有端点,无限长,不可以度量,所以一条直线长10米,此说法错误。
故答案为:×
【点睛】此题考查了线段、射线和直线的含义,应灵活运用。
17.×
【分析】电视屏幕只会放大角两边的长度,不会改变角的度数,依此判断即可。
【详解】在电视屏幕上将角放大,角的度数没有改变。
故答案为:×
【点睛】熟练掌握电视屏幕放大角的特点是解答此题的关键。
18.∠2=125°;∠3=55°;∠4=35°
【分析】根据图意可知∠1和∠2组成了平角,∠2和∠3组成了平角,∠1和∠4组成了直角;据此解答。
【详解】∠4=90°-∠1
=90°-55°
=35°
∠2=180°-∠1
=180°-55°
=125°
∠3=180°-∠2
=180°-125°
=55°
答:∠2=125°;∠3=55°;∠4=35°。
【点睛】解答本题的关键是从∠1入手看哪几个角组成的是直角和平角,再进行计算。
19.;钝角。
【分析】画一条射线,使量角器的中心和射线的端点重合,0°刻度线和射线重合。在量角器110°刻度线的地方点一个点。以画出的射线的端点为端点,通过刚画的点,再画一条射线。据此画出110°的角。大于90°小于180°的角叫钝角,则110°的角是钝角。
【详解】用量角器画一个110°的角,如图所示:
根据钝角的定义可知,它是钝角。
答:它是钝角。
【点睛】熟练掌握角的画法和钝角的定义,注意平时基础知识的积累。
20.∠1=45° ∠2=135° ∠3=45° ∠4=135°
【解析】略
21.如图所示:
①从点走到对边,沿走最近;
②过点作出边的平行线,如图:
③测量出的度数为;
【详解】①根据从直线外一点到这条直线的所有连线中,垂线段最短;由此过点向作垂线,交于点;
②三角板的一条直角边与已知直线重合,用直尺靠紧三角板的另一条直角边,沿直尺移动三角板,使三角板和已知直线重合的直角边和点重合,过点沿三角板的直角边画直线即可;
③用量角器的刻度线对准所量角的一条边,用中心点对准顶点,看看另一条边在哪一刻度这个角就是几度.
22.锐角最小为2°钝角最小为92°
【详解】因为都是整度数,所以最大钝角为179°,大于平角的最小度数为181°,由此得出:181°-179°=2° 钝角最小为92° 181°-89°=92°
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
