第十一章 三角形单元复习题2023-2024学年人教版八年级数学上册(含答案)
文档属性
| 名称 | 第十一章 三角形单元复习题2023-2024学年人教版八年级数学上册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 147.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-14 15:41:42 | ||
图片预览


文档简介
第十一章 三角形 单元复习题
一.选择题
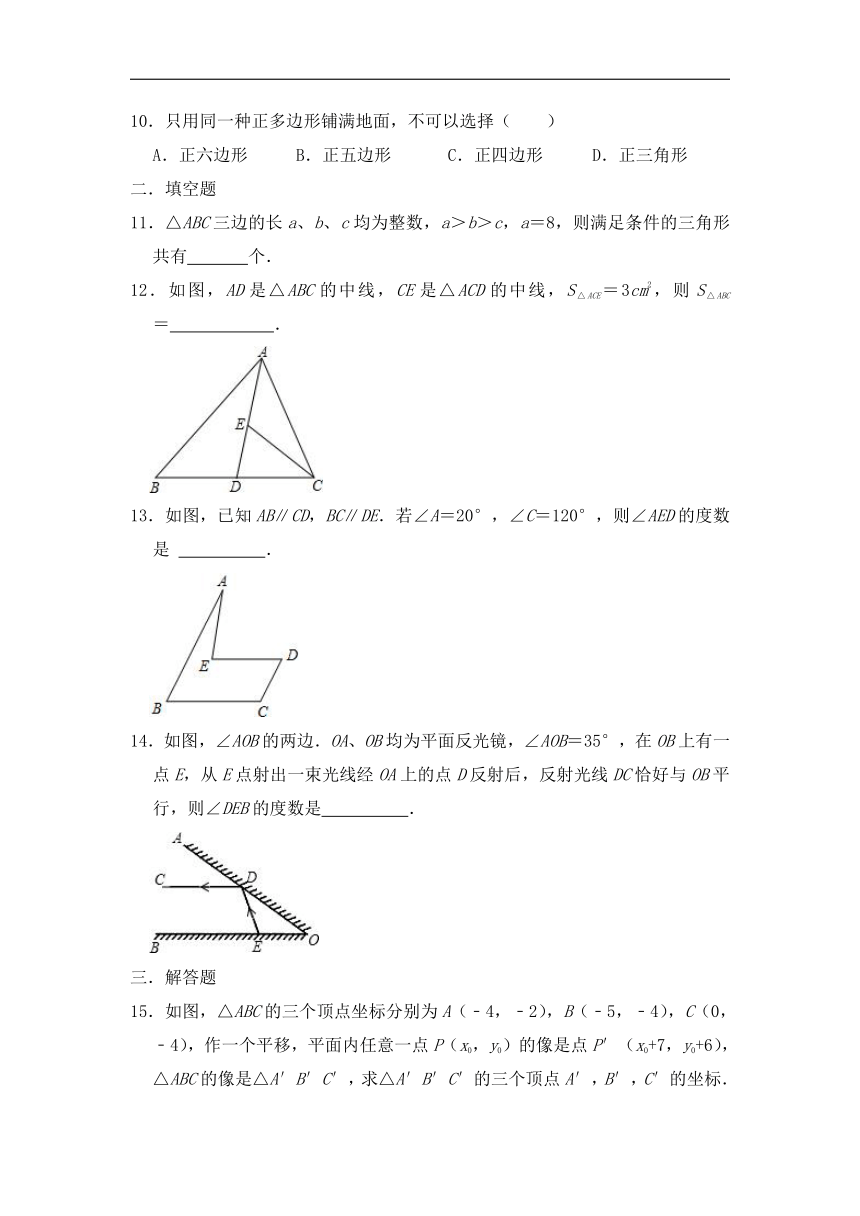
1.已知某三角形的周长为24,且三角形一边的长是另一边长的两倍,则它最小边的长可能是( )
A.3 B.4 C.5 D.6
2.已知,在Rt△ABC中,∠ACB=90°,点D,E分别是AB,BC的中点,延长AC到F,使得CF=AC,连接EF.若EF=4,则AB的长为( )
A.8 B.4 C.4 D.
3.下列图中不是凸多边形的是( )
A. B.
C. D.
4.已知如图DC∥EG,∠C=40°,∠A=70°,则∠AFE的度数为( )
A.140° B.110° C.90° D.30°
5.如图为矩形ABCD,一条直线将该矩形分割成两个多边形,若这两个多边形的内角和分别为a和b,则a+b不可能是( )
A.360° B.540° C.630° D.720°
6.如图,已知∠MON及其边上一点A.以点A为圆心,AO长为半径画弧,分别交OM,ON于点B和C,再以点C为圆心,AC长为半径画弧,恰好经过点B.错误的结论是( )
A.S△AOC=S△ABC B.∠OCB=90°
C.∠MON=30° D.OC=2BC
7.如图,AD是△ABC的高,BE是△ABC的角平分线,BE,AD相交于点F,已知∠BAD=42°,则∠BFD=( )
A.45° B.54° C.56° D.66°
8.六边形的对角线的条数是( )
A.7 B.8 C.9 D.10
9.有公共顶点A,B的正五边形和正六边形按如图所示位置摆放,连接AC交正六边形于点D,则∠ADE的度数为( )
A.144° B.84° C.74° D.54°
10.只用同一种正多边形铺满地面,不可以选择( )
A.正六边形 B.正五边形 C.正四边形 D.正三角形
二.填空题
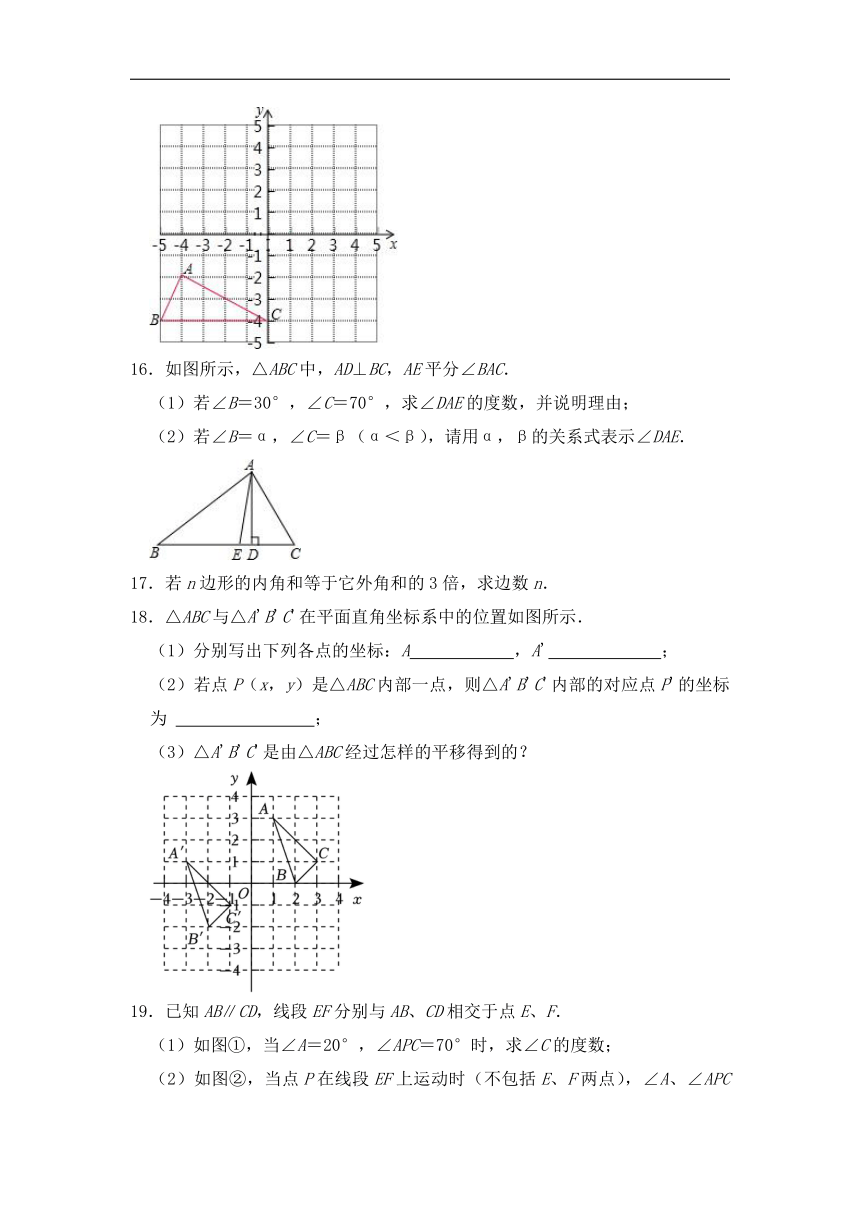
11.△ABC三边的长a、b、c均为整数,a>b>c,a=8,则满足条件的三角形共有 个.
12.如图,AD是△ABC的中线,CE是△ACD的中线,S△ACE=3cm2,则S△ABC= .
13.如图,已知AB∥CD,BC∥DE.若∠A=20°,∠C=120°,则∠AED的度数是 .
14.如图,∠AOB的两边.OA、OB均为平面反光镜,∠AOB=35°,在OB上有一点E,从E点射出一束光线经OA上的点D反射后,反射光线DC恰好与OB平行,则∠DEB的度数是 .
三.解答题
15.如图,△ABC的三个顶点坐标分别为A(﹣4,﹣2),B(﹣5,﹣4),C(0,﹣4),作一个平移,平面内任意一点P(x0,y0)的像是点P′(x0+7,y0+6),△ABC的像是△A′B′C′,求△A′B′C′的三个顶点A′,B′,C′的坐标.
16.如图所示,△ABC中,AD⊥BC,AE平分∠BAC.
(1)若∠B=30°,∠C=70°,求∠DAE的度数,并说明理由;
(2)若∠B=α,∠C=β(α<β),请用α,β的关系式表示∠DAE.
17.若n边形的内角和等于它外角和的3倍,求边数n.
18.△ABC与△A'B'C'在平面直角坐标系中的位置如图所示.
(1)分别写出下列各点的坐标:A ,A' ;
(2)若点P(x,y)是△ABC内部一点,则△A'B'C'内部的对应点P'的坐标为 ;
(3)△A'B'C'是由△ABC经过怎样的平移得到的?
19.已知AB∥CD,线段EF分别与AB、CD相交于点E、F.
(1)如图①,当∠A=20°,∠APC=70°时,求∠C的度数;
(2)如图②,当点P在线段EF上运动时(不包括E、F两点),∠A、∠APC与∠C之间有怎样的数量关系?试证明你的结论;
(3)如图③,当点P在线段EF的延长线上运动时,(2)中的结论还成立吗?如果成立,请说明理由;如果不成立,试探究它们之间新的数量关系并证明.
20.【知识回顾】:如图①,在△ABC中,根据三角形内角和定理,我们知道∠A+∠B+∠C=180°.
如图②,在△ABC中,点D为BC延长线上一点,则∠ACD为△ABC的一个外角.请写出∠ACD与∠A、∠B的关系,直接填空:∠ACD= .
【初步运用】:如图③,点D、E分别是△ABC的边AB、AC延长线上一点.
(1)若∠A=70°,∠DBC=150°,则∠ACB= °.(直接写出答案)
(2)若∠A=70°,则∠DBC+∠ECB= °.(直接写出答案)
【拓展延伸】:如图④,点D、E分别是四边形ABPC的边AB、AC延长线上一点.
(1)若∠A=70°,∠P=150°,则∠DBP+∠ECP= °.(请说明理由)
(2)分别作∠DBP和∠ECP的平分线,交于点O,如图⑤,若∠O=40°,求出∠A和∠P之间的数量关系,并说明理由.
(3)分别作∠DBP和∠ECP的平分线BM、CN,如图⑥,若∠A=∠P,求证:BM∥CN.
答案
1-10.CAABCDDCBB
11.9
12.12cm2
13.80°
14.70°
15.A′(3,4),B′(2,2),C′(7,2)
16.(1)20°
(2)
17.8
18.(1)(1,3),(﹣3,1);
(2)(x﹣4,y﹣2);
(3)△ABC向左平移4个单位,再向下平移2个单位得到△A'B'C
19.
(1)解:过P作PO∥AB,
∵AB∥CD,
∴AB∥PO∥CD,
∵∠A=20°,
∴∠APO=∠A=20°,∠C=∠CPO,
∵∠APC=70°
∴∠C=∠CPO=∠APC﹣∠APO=70°﹣20°=50°;
(2)∠A+∠C=∠APC
证明:过P作PO∥AB
∵AB∥CD,
∴AB∥PO∥CD,
∴∠APO=∠A,∠C=∠CPO,
∴∠APC=∠APO+∠CPO=∠A+∠C;
(3)解:不成立,∠A﹣∠C=∠APC
理由是:过P作PO∥AB,
∵AB∥CD,
∴AB∥PO∥CD,
∴∠APO=∠A,∠C=∠CPO,
∴∠A﹣∠C=∠APO﹣∠CPO=∠APC,
即∠A﹣∠C=∠APC.
20.【知识回顾】∠A+∠B
【初步运用】(1)80(2)250
【拓展延伸】(1)220
(2)∠A和∠P之间的数量关系是:∠P=∠A+80°,
理由是:如图⑤,设∠DBO=x,∠OCE=y,则∠OBP=∠DBO=x,∠PCO=∠OCE=y,
由(1)同理得:x+y=∠A+∠O,2x+2y=∠A+∠P,
2∠A+2∠O=∠A+∠P,
∵∠O=40°,
∴∠P=∠A+80°;
(3)证明:如图,延长BP交CN于点Q,
∵BM平分∠DBP,CN平分∠ECP,
∴∠DBP=2∠MBP,∠ECP=2∠NCP,
∵∠DBP+∠ECP=∠A+∠BPC,
∠A=∠BPC,
∴2∠MBP+2∠NCP=∠A+∠BPC=2∠BPC,
∴∠BPC=∠MBP+∠NCP,
∵∠BPC=∠PQC+∠NCP,
∴∠MBP=∠PQC,
∴BM∥CN.
一.选择题
1.已知某三角形的周长为24,且三角形一边的长是另一边长的两倍,则它最小边的长可能是( )
A.3 B.4 C.5 D.6
2.已知,在Rt△ABC中,∠ACB=90°,点D,E分别是AB,BC的中点,延长AC到F,使得CF=AC,连接EF.若EF=4,则AB的长为( )
A.8 B.4 C.4 D.
3.下列图中不是凸多边形的是( )
A. B.
C. D.
4.已知如图DC∥EG,∠C=40°,∠A=70°,则∠AFE的度数为( )
A.140° B.110° C.90° D.30°
5.如图为矩形ABCD,一条直线将该矩形分割成两个多边形,若这两个多边形的内角和分别为a和b,则a+b不可能是( )
A.360° B.540° C.630° D.720°
6.如图,已知∠MON及其边上一点A.以点A为圆心,AO长为半径画弧,分别交OM,ON于点B和C,再以点C为圆心,AC长为半径画弧,恰好经过点B.错误的结论是( )
A.S△AOC=S△ABC B.∠OCB=90°
C.∠MON=30° D.OC=2BC
7.如图,AD是△ABC的高,BE是△ABC的角平分线,BE,AD相交于点F,已知∠BAD=42°,则∠BFD=( )
A.45° B.54° C.56° D.66°
8.六边形的对角线的条数是( )
A.7 B.8 C.9 D.10
9.有公共顶点A,B的正五边形和正六边形按如图所示位置摆放,连接AC交正六边形于点D,则∠ADE的度数为( )
A.144° B.84° C.74° D.54°
10.只用同一种正多边形铺满地面,不可以选择( )
A.正六边形 B.正五边形 C.正四边形 D.正三角形
二.填空题
11.△ABC三边的长a、b、c均为整数,a>b>c,a=8,则满足条件的三角形共有 个.
12.如图,AD是△ABC的中线,CE是△ACD的中线,S△ACE=3cm2,则S△ABC= .
13.如图,已知AB∥CD,BC∥DE.若∠A=20°,∠C=120°,则∠AED的度数是 .
14.如图,∠AOB的两边.OA、OB均为平面反光镜,∠AOB=35°,在OB上有一点E,从E点射出一束光线经OA上的点D反射后,反射光线DC恰好与OB平行,则∠DEB的度数是 .
三.解答题
15.如图,△ABC的三个顶点坐标分别为A(﹣4,﹣2),B(﹣5,﹣4),C(0,﹣4),作一个平移,平面内任意一点P(x0,y0)的像是点P′(x0+7,y0+6),△ABC的像是△A′B′C′,求△A′B′C′的三个顶点A′,B′,C′的坐标.
16.如图所示,△ABC中,AD⊥BC,AE平分∠BAC.
(1)若∠B=30°,∠C=70°,求∠DAE的度数,并说明理由;
(2)若∠B=α,∠C=β(α<β),请用α,β的关系式表示∠DAE.
17.若n边形的内角和等于它外角和的3倍,求边数n.
18.△ABC与△A'B'C'在平面直角坐标系中的位置如图所示.
(1)分别写出下列各点的坐标:A ,A' ;
(2)若点P(x,y)是△ABC内部一点,则△A'B'C'内部的对应点P'的坐标为 ;
(3)△A'B'C'是由△ABC经过怎样的平移得到的?
19.已知AB∥CD,线段EF分别与AB、CD相交于点E、F.
(1)如图①,当∠A=20°,∠APC=70°时,求∠C的度数;
(2)如图②,当点P在线段EF上运动时(不包括E、F两点),∠A、∠APC与∠C之间有怎样的数量关系?试证明你的结论;
(3)如图③,当点P在线段EF的延长线上运动时,(2)中的结论还成立吗?如果成立,请说明理由;如果不成立,试探究它们之间新的数量关系并证明.
20.【知识回顾】:如图①,在△ABC中,根据三角形内角和定理,我们知道∠A+∠B+∠C=180°.
如图②,在△ABC中,点D为BC延长线上一点,则∠ACD为△ABC的一个外角.请写出∠ACD与∠A、∠B的关系,直接填空:∠ACD= .
【初步运用】:如图③,点D、E分别是△ABC的边AB、AC延长线上一点.
(1)若∠A=70°,∠DBC=150°,则∠ACB= °.(直接写出答案)
(2)若∠A=70°,则∠DBC+∠ECB= °.(直接写出答案)
【拓展延伸】:如图④,点D、E分别是四边形ABPC的边AB、AC延长线上一点.
(1)若∠A=70°,∠P=150°,则∠DBP+∠ECP= °.(请说明理由)
(2)分别作∠DBP和∠ECP的平分线,交于点O,如图⑤,若∠O=40°,求出∠A和∠P之间的数量关系,并说明理由.
(3)分别作∠DBP和∠ECP的平分线BM、CN,如图⑥,若∠A=∠P,求证:BM∥CN.
答案
1-10.CAABCDDCBB
11.9
12.12cm2
13.80°
14.70°
15.A′(3,4),B′(2,2),C′(7,2)
16.(1)20°
(2)
17.8
18.(1)(1,3),(﹣3,1);
(2)(x﹣4,y﹣2);
(3)△ABC向左平移4个单位,再向下平移2个单位得到△A'B'C
19.
(1)解:过P作PO∥AB,
∵AB∥CD,
∴AB∥PO∥CD,
∵∠A=20°,
∴∠APO=∠A=20°,∠C=∠CPO,
∵∠APC=70°
∴∠C=∠CPO=∠APC﹣∠APO=70°﹣20°=50°;
(2)∠A+∠C=∠APC
证明:过P作PO∥AB
∵AB∥CD,
∴AB∥PO∥CD,
∴∠APO=∠A,∠C=∠CPO,
∴∠APC=∠APO+∠CPO=∠A+∠C;
(3)解:不成立,∠A﹣∠C=∠APC
理由是:过P作PO∥AB,
∵AB∥CD,
∴AB∥PO∥CD,
∴∠APO=∠A,∠C=∠CPO,
∴∠A﹣∠C=∠APO﹣∠CPO=∠APC,
即∠A﹣∠C=∠APC.
20.【知识回顾】∠A+∠B
【初步运用】(1)80(2)250
【拓展延伸】(1)220
(2)∠A和∠P之间的数量关系是:∠P=∠A+80°,
理由是:如图⑤,设∠DBO=x,∠OCE=y,则∠OBP=∠DBO=x,∠PCO=∠OCE=y,
由(1)同理得:x+y=∠A+∠O,2x+2y=∠A+∠P,
2∠A+2∠O=∠A+∠P,
∵∠O=40°,
∴∠P=∠A+80°;
(3)证明:如图,延长BP交CN于点Q,
∵BM平分∠DBP,CN平分∠ECP,
∴∠DBP=2∠MBP,∠ECP=2∠NCP,
∵∠DBP+∠ECP=∠A+∠BPC,
∠A=∠BPC,
∴2∠MBP+2∠NCP=∠A+∠BPC=2∠BPC,
∴∠BPC=∠MBP+∠NCP,
∵∠BPC=∠PQC+∠NCP,
∴∠MBP=∠PQC,
∴BM∥CN.
