第六章幂函数、指数函数和对数函数 复习课讲义(含答案)
文档属性
| 名称 | 第六章幂函数、指数函数和对数函数 复习课讲义(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 449.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-13 00:00:00 | ||
图片预览



文档简介
编号:037 课题:§6 幂函数、指数函数和对数函数复习课
教学课时安排
1、上课时间:_________________.
2、课时安排:_________________.
3、上课班级___________________.
学科目标要求
1.理解并掌握幂、指数、对数函数的图象问题;
2.会利用幂、指数、对数函数的性质比较大小;
3.理解并掌握幂、指数、对数函数的性质应用;
4.解决一些抽象函数应用问题.
本节重点难点
重点:幂、指数、对数函数的性质应用;
难点:抽象函数应用问题.
学科素养目标
指数函数、对数函数、幂函数是与现实世界的密切联系的函数模型,是体验函数模型运用过程和方法的重要载体.通过学习,进一步体会函数在数学和其他学科中的重要性,初步运用函数思想理解和处理现实生活和社会中的简单问题,利用函数的性质求方程的近似解,体会函数与方程的有机联系.
在学习基本初等函数I及其应用的过程中,要通过对具体数式的分析,使学生体会分数指数幂、对数的概念和意义,掌握有理指数幂、对数的运算性质,了解并掌握指数函数、对数函数、幂函数的概念、图象和性质;知道指数函数、对数函数、幂函数是描述客观世界变化规律的重要数学模型.
通过函数的应用,了解函数与方程之间的关系,体会二分法求一些简单方程的近似解的方法,尽管这个解也许不准确,但可以通过有效的方法控制精确度;通过数据拟合,体会到现代信息技术是数学课程的一个重要部分;会利用函数知识分析问题、解决问题,能准确、清晰、有条理地表述问题以及问题的解决过程,使学生明白函数与方程是研究事物变化的重要工具,逐步形成利用运动、变化的观点观察事物的理性思维能力、辩证思维能力、分析问题和解决问题的能力,以及数学表达、交流的能力,进一步培养学生的创新意识与探究能力、数学建模能力和实践能力.
知识结构简图
教学过程赏析
基础知识积累
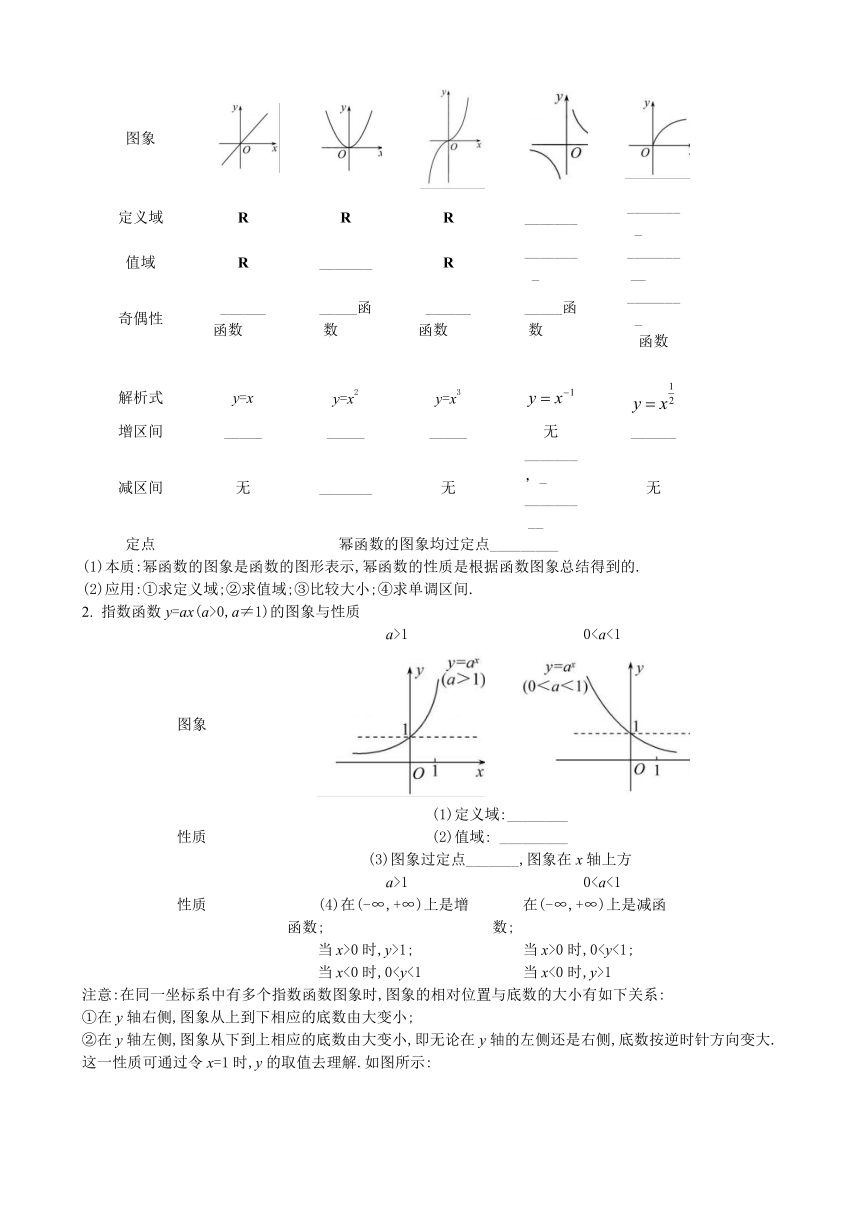
1.常见幂函数的图象与性质
解析式 y=x y=x2 y=x3
图象
定义域 R R R _______ ________
值域 R _______ R ________ _________
奇偶性 ______函数 _____函数 ______函数 _____函数 ________ 函数
解析式 y=x y=x2 y=x3
增区间 _____ _____ _____ 无 ______
减区间 无 _______ 无 _______,_ _________ 无
定点 幂函数的图象均过定点_________
(1)本质:幂函数的图象是函数的图形表示,幂函数的性质是根据函数图象总结得到的.
(2)应用:①求定义域;②求值域;③比较大小;④求单调区间.
2. 指数函数y=ax(a>0,a≠1)的图象与性质
a>1 0图象
性质 (1)定义域:________
(2)值域: _________
(3)图象过定点_______,图象在x轴上方
a>1 0性质 (4)在(-∞,+∞)上是增函数; 当x>0时,y>1; 当x<0时,00时,01
注意:在同一坐标系中有多个指数函数图象时,图象的相对位置与底数的大小有如下关系:
①在y轴右侧,图象从上到下相应的底数由大变小;
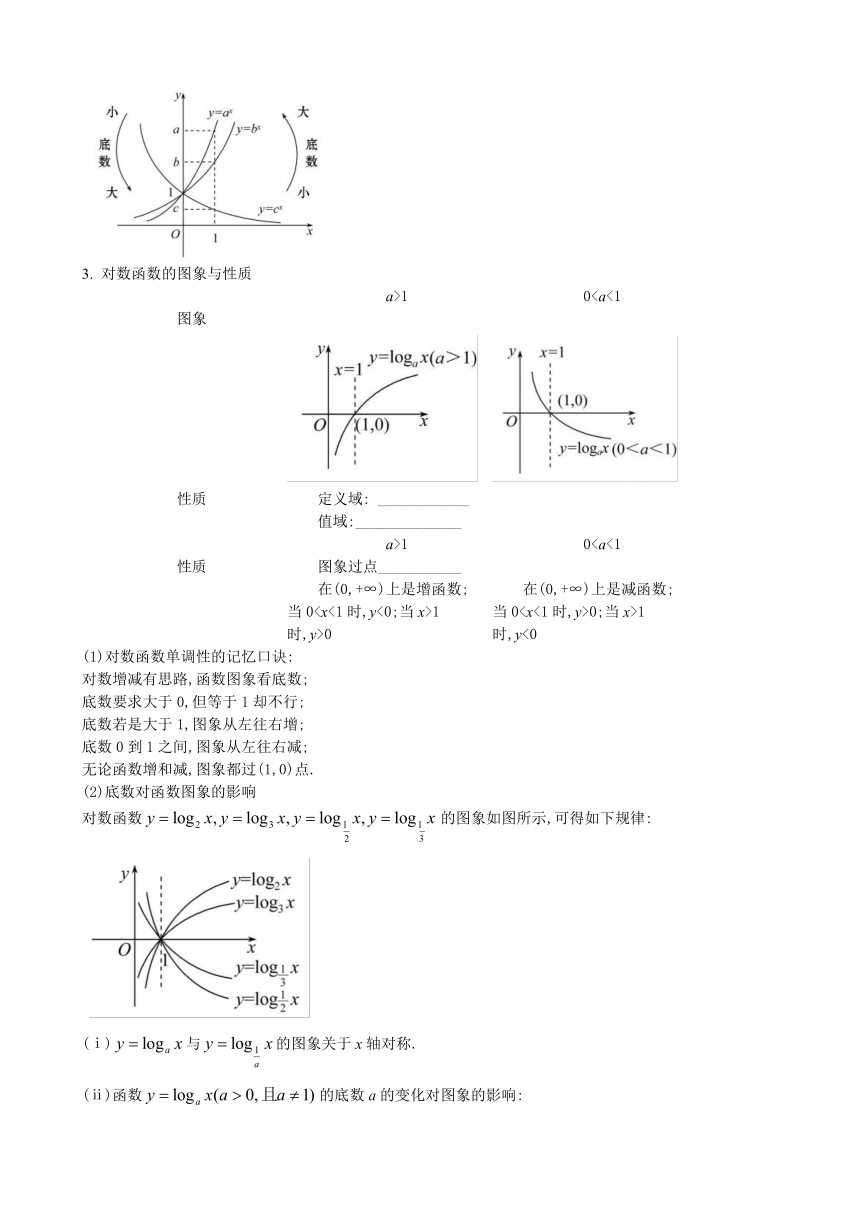
②在y轴左侧,图象从下到上相应的底数由大变小,即无论在y轴的左侧还是右侧,底数按逆时针方向变大.这一性质可通过令x=1时,y的取值去理解.如图所示:
3. 对数函数的图象与性质
a>1 0图象
性质 定义域: ____________
值域:______________
a>1 0性质 图象过点___________
在(0,+∞)上是增函数;当01时,y>0 在(0,+∞)上是减函数;当00;当x>1时,y<0
(1)对数函数单调性的记忆口诀:
对数增减有思路,函数图象看底数;
底数要求大于0,但等于1却不行;
底数若是大于1,图象从左往右增;
底数0到1之间,图象从左往右减;
无论函数增和减,图象都过(1,0)点.
(2)底数对函数图象的影响
对数函数的图象如图所示,可得如下规律:
(ⅰ)与的图象关于x轴对称.
(ⅱ)函数的底数a的变化对图象的影响:
①上下比较:在直线x=1的右侧,当a>1时,底数越大图象越靠近x轴;当0底数越小图象越靠近x轴.
②左右比较:交点(图象与y=1的交点)的横坐标越大,对应的对数函数的底数a越
大.
【课堂题组训练】
题1. 已知幂函数y=f(x)的图象经过点(-2,-),则满足f(x)=27的x的值为( )
A.3 B. C.27 D.
题2.已知log2x=log3y=log5z>1,则,,的大小排序为( )
A.<< B.<<
C.<< D.<<
题3.已知f(x)=lg (e|x|+2),a=20.3,b=log32,c=log2,则f(a),f(b),f(c)的大小关系为( )
A.f(b)>f(a)>f(c)
B.f(c)>f(a)>f(b)
C.f(a)>f(b)>f(c)
D.f(c)>f(b)>f(a)
题4.函数f(x)=ax2+2x+1与g(x)=xa在同一坐标系中的图象不可能为( )
题5.已知实数a,b满足等式2a=3b,下列关系式中不可能成立的是( )
A.0<b<a B.a<b<0
C.b<a<0 D.a=b
题6.下列说法中错误的个数是( )
①幂函数的图象不过第四象限;
②y=x0的图象是一条直线;
③若函数y=的定义域是,则它的值域是;
④若函数y=x2的值域是,则它的定义域一定是.
A.1 B.2 C.3 D.4
题7.已知f(x)=3x-,若f(m)+f(n)>0,则( )
A.m+n>0 B.m+n<0
C.m-n>0 D.m-n<0
题8.对于函数f(x),若在定义域内存在实数x0满足f(-x0)=-f(x0),则称函数f(x)为“倒戈函数”.设f(x)=3x+m-1(m∈R,m≠0)是定义在[-1,1]上的“倒戈函数”,则实数m的取值范围是( )
A.[-,0) B.[-,-]
C.[-,0] D.(-∞,0)
题9(多选题).已知幂函数f(x)的图象经过(27,),则幂函数f(x)具有的性质是( )
A.在其定义域上为增函数
B.在(0,+∞)上单调递减
C.奇函数
D.定义域为R
题10(多选题).已知函数f(x)=log3在区间(-3,3]上单调递减,则实数a的可取值是( )
A.-1 B.-3 C.0 D.5
题11(多选题).行列式作为基本的数学工具,有着重要的应用,行列式=ad-bc,则下列说法正确的是( )
A.函数f(x)=的值域为[-7,+∞)
B.不等式≥0的解集为[1,+∞)
C.行列式=0是“a=c=0或b=d=0”的必要不充分条件
D.若f(x)=为奇函数,则fi(x)(i=1,2,3,4)均为奇函数
题12(多选题).已知函数f(x)=,g(x)=lg (-x),则( )
A.函数f(x)为偶函数
B.函数g(x)为奇函数
C.函数F(x)=f(x)+g(x)在区间[-1,1]上的最大值与最小值之和为0
D.设F(x)=f(x)+g(x),则F(2a)+F(-1-a)<0的解集为(1,+∞)
题13(多选题).设f(x)=,x∈R,则f(x)是 ( )
A.奇函数且在(-∞,0)上是增函数 B.偶函数且在(-∞,0)上是增函数
C.奇函数且在(0,+∞)上是减函数 D.偶函数且在(0,+∞)上是减函数
题14(多选题).若函数f(x)=ex-e2-x,则下列叙述正确的是 ( )
A.f(x)在(-∞,+∞)上单调递增 B.f(x)的值域为(0,+∞)
C.y=f(x)的图象关于直线x=1对称 D.y=f(x)的图象关于点(1,0)对称
题15(多选题).已知函数f(x)=下列结论正确的是 ( )
A.若f(a)=1,则a=3 B.f=2 020
C.若f(a)≥2,则a≤-1或a≥5 D.若方程f(x)=k有两个不同的实数根,则k>
题16.函数y=+的定义域为____________.
题17.已知125x=12.5y=1 000,则=________.
题18.f(x)=x-x,则满足f(x)>0的x的取值范围为____________.
题19.已知函数y=()mt-7(m为常数),当t=4时,y=64,若y≤,则实数t的取值范围为__________.
题20.已知函数f(x)=2x-.
(1)若f(x)=2,求2x的值;
(2)若2tf(2t)+mf(t)≥0,对于任意t∈[1,2]恒成立,求实数m的取值范围.
题21.已知f(x)是定义在R上的偶函数,且x≤0时,f(x)=log (-x+1).
(1)求函数f(x)的解析式;
(2)若f(a-1)<-1,求实数a的取值范围.
题22.已知函数f(x)=|log2x|.
(1)若x1<x2,且f(x1)=f(x2),求证:+++>3;
(2)解不等式:f(f(x))>1.
题23.已知函数f(x)是偶函数,且当x≥0时,f(x)=loga(3-ax)(a>0,且a≠1).
(1)求x<0时f(x)的解析式;
(2)在①f(x)在(1,4)上单调递增,②在区间(-1,1)上恒有f(x)≥x2这两个条件中任选一个补充到本题中,求g(a)=()a的取值范围.
注:如果选择多个条件分别解答,按第一个解答计分.
编号:037 课题:§6 幂函数、指数函数和对数函数复习课
教学课时安排
1、上课时间:_________________.
2、课时安排:_________________.
3、上课班级___________________.
学科目标要求
1.理解并掌握幂、指数、对数函数的图象问题;
2.会利用幂、指数、对数函数的性质比较大小;
3.理解并掌握幂、指数、对数函数的性质应用;
4.解决一些抽象函数应用问题.
本节重点难点
重点:幂、指数、对数函数的性质应用;
难点:抽象函数应用问题.
学科素养目标
指数函数、对数函数、幂函数是与现实世界的密切联系的函数模型,是体验函数模型运用过程和方法的重要载体.通过学习,进一步体会函数在数学和其他学科中的重要性,初步运用函数思想理解和处理现实生活和社会中的简单问题,利用函数的性质求方程的近似解,体会函数与方程的有机联系.
在学习基本初等函数I及其应用的过程中,要通过对具体数式的分析,使学生体会分数指数幂、对数的概念和意义,掌握有理指数幂、对数的运算性质,了解并掌握指数函数、对数函数、幂函数的概念、图象和性质;知道指数函数、对数函数、幂函数是描述客观世界变化规律的重要数学模型.
通过函数的应用,了解函数与方程之间的关系,体会二分法求一些简单方程的近似解的方法,尽管这个解也许不准确,但可以通过有效的方法控制精确度;通过数据拟合,体会到现代信息技术是数学课程的一个重要部分;会利用函数知识分析问题、解决问题,能准确、清晰、有条理地表述问题以及问题的解决过程,使学生明白函数与方程是研究事物变化的重要工具,逐步形成利用运动、变化的观点观察事物的理性思维能力、辩证思维能力、分析问题和解决问题的能力,以及数学表达、交流的能力,进一步培养学生的创新意识与探究能力、数学建模能力和实践能力.
知识结构简图
教学过程赏析
基础知识积累
1.常见幂函数的图象与性质
解析式 y=x y=x2 y=x3
图象
定义域 R R R _{x|x≠0}_ __[0,+∞)__
值域 R __[0,+∞)_ R _{y|y≠0}_ __[0,+∞)__
奇偶性 _ 奇__函数 __偶_函数 __奇_函数 _奇__函数 __非奇非偶_ 函数
解析式 y=x y=x2 y=x3
增区间 __ __[0,+∞)_ __ 无 __[0,+∞)__
减区间 无 __(-∞,0)__ 无 __(-∞,0),_ __(0,+∞)__ 无
定点 幂函数的图象均过定点__(1,1)_
(1)本质:幂函数的图象是函数的图形表示,幂函数的性质是根据函数图象总结得到的.
(2)应用:①求定义域;②求值域;③比较大小;④求单调区间.
2. 指数函数y=ax(a>0,a≠1)的图象与性质
a>1 0图象
性质 (1)定义域:_ _
(2)值域: ___ __
(3)图象过定点__ __,图象在x轴上方
a>1 0性质 (4)在(-∞,+∞)上是增函数; 当x>0时,y>1; 当x<0时,00时,01
注意:在同一坐标系中有多个指数函数图象时,图象的相对位置与底数的大小有如下关系:
①在y轴右侧,图象从上到下相应的底数由大变小;
②在y轴左侧,图象从下到上相应的底数由大变小,即无论在y轴的左侧还是右侧,底数按逆时针方向变大.这一性质可通过令x=1时,y的取值去理解.如图所示:
3. 对数函数的图象与性质
a>1 0图象
性质 定义域: ___(0,+∞)_____
值域: ________
a>1 0性质 图象过点___(1,0)____
在(0,+∞)上是增函数;当01时,y>0 在(0,+∞)上是减函数;当00;当x>1时,y<0
(1)对数函数单调性的记忆口诀:
对数增减有思路,函数图象看底数;
底数要求大于0,但等于1却不行;
底数若是大于1,图象从左往右增;
底数0到1之间,图象从左往右减;
无论函数增和减,图象都过(1,0)点.
(2)底数对函数图象的影响
对数函数的图象如图所示,可得如下规律:
(ⅰ)与的图象关于x轴对称.
(ⅱ)函数的底数a的变化对图象的影响:
①上下比较:在直线x=1的右侧,当a>1时,底数越大图象越靠近x轴;当0底数越小图象越靠近x轴.
②左右比较:交点(图象与y=1的交点)的横坐标越大,对应的对数函数的底数a越
大.
【课堂题组训练】
题1. 已知幂函数y=f(x)的图象经过点(-2,-),则满足f(x)=27的x的值为( )
A.3 B. C.27 D.
【解析】选D.因为幂函数y=xα的图象经过点(-2,-),所以(-2)α=-,所以α=-3.
又因为f(x)=27,所以x-3=27,所以x=.
题2.已知log2x=log3y=log5z>1,则,,的大小排序为( )
A.<< B.<<
C.<< D.<<
【解析】选D.由log2x=log3y=log5z>1,
得1-log2x=1-log3y=1-log5z<0,即
log2=log3=log5<0,
可得<<.
题3.已知f(x)=lg (e|x|+2),a=20.3,b=log32,c=log2,则f(a),f(b),f(c)的大小关系为( )
A.f(b)>f(a)>f(c)
B.f(c)>f(a)>f(b)
C.f(a)>f(b)>f(c)
D.f(c)>f(b)>f(a)
【解析】选B.f(-x)=lg (e|-x|+2)=lg (e|x|+2)=f(x),f(x)是偶函数,
x≥0时f(x)=lg (ex+2)是增函数,1<20.3<2,0<log32<1,log2=-2,f(log2)=f(-2)=f(2),
而log32<20.3<2,所以f(log32)<f(20.3)<f(2),即f(b)<f(a)<f(c).
题4.函数f(x)=ax2+2x+1与g(x)=xa在同一坐标系中的图象不可能为( )
【解析】选B.当a=-1时,g(x)=xa为奇函数,定义域为,且在(0,
+∞)上递减,而f(x)=ax2+2x+1开口向下,对称轴为x=->0,
f(0)=1,故A符合,B不符合;
当a=2n(n∈N+)时,g(x)=xa为偶函数,且在(0,+∞)上递增,f(x)=ax2+2x+1开口向上,且对称轴为x=-<0,Δ=4-4a<0,其图象和x轴没有交点,故D符合;
当a=(n∈N+)时,函数g(x)=xa的定义域为[0,+∞),且在[0,+∞)上递增,f(x)=ax2+2x+1开口向上且对称轴为x=-<0,Δ=4-4a>0,图象和x轴有两个交点,故C符合.
题5.已知实数a,b满足等式2a=3b,下列关系式中不可能成立的是( )
A.0<b<a B.a<b<0
C.b<a<0 D.a=b
【解析】选C.作出函数y=2x与函数y=3x的图象,如图,当2a=3b>1时根据图象得0<b<a,故A选项正确,不符合题意;
当2a=3b=1时,根据图象得a=b=0,故D选项正确,不符合题意;
当2a=3b<1时根据图象得a<b<0,故B选项正确,不符合题意;故不可能成立的是b<a<0.
题6.下列说法中错误的个数是( )
①幂函数的图象不过第四象限;
②y=x0的图象是一条直线;
③若函数y=的定义域是,则它的值域是;
④若函数y=x2的值域是,则它的定义域一定是.
A.1 B.2 C.3 D.4
【解析】选C.由幂函数的图象与性质知①正确;
y=x0的图象是直线y=1上去掉点(0,1),②错误;
函数y=的定义域是,则它的值域是,③错误;
若函数y=x2的值域是,则它的定义域也可能是,④错误.
题7.已知f(x)=3x-,若f(m)+f(n)>0,则( )
A.m+n>0 B.m+n<0
C.m-n>0 D.m-n<0
【解析】选A.因为f(x)=3x-,x∈R,所以f(-x)=3-x-=
x-3x=-f(x),所以f(x)是定义域为R的奇函数,且是增函数;又f(m)+f(n)>0,所以f(m)>-f(n)=f(-n),所以m>-n,所以m+n>0.
题8.对于函数f(x),若在定义域内存在实数x0满足f(-x0)=-f(x0),则称函数f(x)为“倒戈函数”.设f(x)=3x+m-1(m∈R,m≠0)是定义在[-1,1]上的“倒戈函数”,则实数m的取值范围是( )
A.[-,0) B.[-,-]
C.[-,0] D.(-∞,0)
【解析】选A.因为f(x)=3x+m-1是定义在[-1,1]上的“倒戈函数,所以存在x0∈[-1,1]满足f(-x0)=-f(x0),所以3+m-1=-3-m+1,
所以2m=-3-3+2,构造函数y=-3-3+2,x0∈[-1,1],
令t=3,t∈[,3],y=--t+2=2-(t+)在[,1]单调递增,
在(1,3]单调递减,所以t=1取得最大值0,t=或t=3取得最小值-,y∈[-,0],
所以-≤2m<0,所以-≤m<0.
题9(多选题).已知幂函数f(x)的图象经过(27,),则幂函数f(x)具有的性质是( )
A.在其定义域上为增函数
B.在(0,+∞)上单调递减
C.奇函数
D.定义域为R
【解析】选BC.设幂函数f(x)=xa,因为幂函数图象过点(27,),所以27a=,所以a=-,所以f(x)=x= (x≠0),所以f(x)定义域为(-∞,0)∪(0,+∞),满足f(-x)=-f(x),是奇函数,值域为(-∞,0)∪(0,+∞),在定义域内不单调,在上单调递减.
题10(多选题).已知函数f(x)=log3在区间(-3,3]上单调递减,则实数a的可取值是( )
A.-1 B.-3 C.0 D.5
【解析】选AC.令u=,由题意可知,u=>0对任意的x∈(-3,3]恒成立,
因为x+3>0,则ax+6>0对任意的x∈(-3,3]恒成立,则,得
-2<a≤2.
因为函数f(x)=log3在区间(-3,3]上单调递减,外层函数y=log3u为增函数,
故内层函数u===a+在区间(-3,3]上为减函数,
所以6-3a>0,可得a<2.综上所述,-2<a<2.
题11(多选题).行列式作为基本的数学工具,有着重要的应用,行列式=ad-bc,则下列说法正确的是( )
A.函数f(x)=的值域为[-7,+∞)
B.不等式≥0的解集为[1,+∞)
C.行列式=0是“a=c=0或b=d=0”的必要不充分条件
D.若f(x)=为奇函数,则fi(x)(i=1,2,3,4)均为奇函数
【解析】选ABC.对于A,f(x)==x(x-2)-6=(x-1)2-7≥-7,故f(x)的值域为[-7,+∞),故A正确;
对于B,≥0 2x-1·4x-2×2≥0 23x-1≥22,解得x≥1,故B正确;
对于C,当“a=c=0或b=d=0”时,可得=0;而当=0时,取a=b=c=d=1,可得“a=c=0或b=d=0”不成立,故C正确;
对于D,若f(x)=为奇函数,取fi(x)(i=1,2,3,4)=x2,可得f(x)=0为R上的奇函数,故D错误.
题12(多选题).已知函数f(x)=,g(x)=lg (-x),则( )
A.函数f(x)为偶函数
B.函数g(x)为奇函数
C.函数F(x)=f(x)+g(x)在区间[-1,1]上的最大值与最小值之和为0
D.设F(x)=f(x)+g(x),则F(2a)+F(-1-a)<0的解集为(1,+∞)
【解析】选BCD.f(x)=,定义域为R,
f(-x)==-=-f(x),
则f(x)为奇函数,故A错误;
g(x)=lg (-x),定义域为R,
g(-x)=lg (-(-x))
=-lg (-x)=-g(x),
则g(x)为奇函数,故B正确;
对于C:F(x)=f(x)+g(x),f(x),g(x)都为奇函数,则F(x)=f(x)+g(x)为奇函数,
F(x)=f(x)+g(x)在区间[-1,1]上的最大值与最小值互为相反数,必有F(x)在区间[-1,1]上的最大值与最小值之和为0,故C正确;
f(x)==-()=-1,则f(x)在R上为减函数,
g(x)=lg (-x)=lg ,
则g(x)在R上为减函数,则F(x)=f(x)+g(x)在R上为减函数,若F(2a)+F(-1-a)<0,即F(2a)<F(1+a),则必有2a>1+a,解得a>1,
即F(2a)+F(-1-a)<0的解集为(1,+∞),故D正确.
题13(多选题).设f(x)=,x∈R,则f(x)是 ( )
A.奇函数且在(-∞,0)上是增函数 B.偶函数且在(-∞,0)上是增函数
C.奇函数且在(0,+∞)上是减函数 D.偶函数且在(0,+∞)上是减函数
【解析】选BD.依题意,得f(-x)===f(x),所以f(x)是偶函数.当x>0时,f(x)==,该指数函数是减函数;当x<0时,f(x)===2x,该指数函数是增函数.
题14(多选题).若函数f(x)=ex-e2-x,则下列叙述正确的是 ( )
A.f(x)在(-∞,+∞)上单调递增 B.f(x)的值域为(0,+∞)
C.y=f(x)的图象关于直线x=1对称 D.y=f(x)的图象关于点(1,0)对称
【解析】选AD.对于A,因为y=ex在(-∞,+∞)上单调递增,y=-e2-x在(-∞,+∞)上单调递增,所以f(x)在(-∞,+∞)上单调递增,故A正确;对于B,f(0)=1-e2<0,故B错误;对于C,f(0)=1-e2,f(2)=e2-1,f(0)≠f(2),所以y=f(x)的图象不关于直线x=1对称,故C错误;对于D,因为f(1+x)=e1+x-e1-x,f(1-x)=e1-x-e1+x,所以f(1+x)+f(1-x)=0,则y=f(x)的图象关于点(1,0)对称,故D正确.
题15(多选题).已知函数f(x)=下列结论正确的是 ( )
A.若f(a)=1,则a=3 B.f=2 020
C.若f(a)≥2,则a≤-1或a≥5 D.若方程f(x)=k有两个不同的实数根,则k>
【解析】选BC.对于A:由f(a)=1,
得 或 解得a=3或a=0,故A错误;
对于B:f=log2=log2=,因为<0,
所以f=f()==2 020,故B正确;
对于C:由f(a)≥2,得 或解得a≥5或a≤-1,故C正确;
对于D:作出f(x)的图象,如图所示:
又f(1)=,结合图象可得f(x)=k有两个不同的实数根,即y=f(x)的图象与y=k的图象有两个交点,所以k≥,故D错误.
题16.函数y=+的定义域为____________.
【解析】由题意,,得,
所以-2≤x<1.
答案:[-2,1)
题17.已知125x=12.5y=1 000,则=________.
【解析】因为125x=12.5y=1 000,
所以x=log125 1 000,y=log12.5 1 000,
=-=log1 000 125-log1 00012.5
=log1 000=log1 000 10=.
答案:
题18.f(x)=x-x,则满足f(x)>0的x的取值范围为____________.
【解析】因为f(x)=x-x>0,所以x>x.
在同一坐标系中作出y=x,y=x的图象,如图所示:
结合幂函数图象可得x∈(-∞,0)∪(1,+∞).
答案:(-∞,0)∪(1,+∞)
题19.已知函数y=()mt-7(m为常数),当t=4时,y=64,若y≤,则实数t的取值范围为__________.
【解析】将t=4,y=64代入y=()mt-7,
可得64=()4m-7,解得m=,所以y=().由()≤,得t-7≥1,解得t≥32.故实数t的取值范围是[32,+∞).
答案:[32,+∞)
题20.已知函数f(x)=2x-.
(1)若f(x)=2,求2x的值;
(2)若2tf(2t)+mf(t)≥0,对于任意t∈[1,2]恒成立,求实数m的取值范围.
【解析】(1)当x<0时,f(x)=0≠2,舍去;
当x≥0时,f(x)=2x-=2,
即(2x)2-2·2x-1=0,2x>0.
解得2x=1+.
(2)当t∈[1,2]时,2tf(2t)+mf(t)≥0,即2t+m(2t-)≥0,
即m(22t-1)≥-(24t-1),因为22t-1>0,所以m≥-(22t+1).
由t∈[1,2],所以-(22t+1)∈[-17,-5].
故m的取值范围是[-5,+∞).
题21.已知f(x)是定义在R上的偶函数,且x≤0时,f(x)=log (-x+1).
(1)求函数f(x)的解析式;
(2)若f(a-1)<-1,求实数a的取值范围.
【解析】(1)令x>0,则-x<0,
f(-x)=log (x+1)=f(x),
所以x>0时,f(x)=log (x+1),
则f(x)=
(2)因为f(x)=log (-x+1)在(-∞,0]上为增函数,所以f(x)在(0,+∞)上为减函数.
因为f(a-1)<-1=f(1),所以|a-1|>1,解得a>2或a<0.
故实数a的取值范围为(-∞,0)∪(2,+∞).
题22.已知函数f(x)=|log2x|.
(1)若x1<x2,且f(x1)=f(x2),求证:+++>3;
(2)解不等式:f(f(x))>1.
【解析】(1)f(x)=|log2x|=作出f(x)=|log2x|的图象如图所示:
由f(x1)=f(x2)可得-log2x1=log2x2,即log2x1+log2x2=0,所以log2(x1x2)=0,可得x1x2=1且x1≠1,
所以+=+=1,而+=+x1≥2=2,当且仅当x1=1时取等号,而x1≠1,所以+>2.
综上:+++>3.
(2)令f(x)=t,由f(t)>1即f(t)=|log2t|>1,可得log2t>1或log2t<-1,
所以0<t<或t>2,所以0<f(x)<或f(x)>2,即0<|log2x|<或|log2x|>2,
由0<|log2x|<,可得-<log2x<且log2x≠0,即log2<log2x<=log2,解得:<x<且x≠1,由|log2x|>2可得log2x>2=log24或log2x<-2=log2,解得0<x<或x>4,
综上:f(f(x))>1的解集为(0,)∪(,1)∪(1,)∪(4,+∞).
题23.已知函数f(x)是偶函数,且当x≥0时,f(x)=loga(3-ax)(a>0,且a≠1).
(1)求x<0时f(x)的解析式;
(2)在①f(x)在(1,4)上单调递增,②在区间(-1,1)上恒有f(x)≥x2这两个条件中任选一个补充到本题中,求g(a)=()a的取值范围.
注:如果选择多个条件分别解答,按第一个解答计分.
【解析】(1)当x<0时,-x>0,因为f(x)是偶函数,所以f(x)=f(-x)=loga(3+ax).所以当x<0时,f(x)=loga(3+ax).
(2)选条件①:由于f(x)在(1,4)上单调递增,所以a>1不合题意.
所以解得0<a≤,
所以g(a)=()a的取值范围是[,1).
选条件②:当0<a<1时,f(0)=loga3<0,显然不满足题意;
当a>1时,因为f(x)与y=x2都是偶函数,所以只需考虑x∈[0,1)时,f(x)≥x2恒成立即可.
由复合函数的单调性可知,函数f(x)在[0,1)上单调递减,而y=x2在[0,1)上单调递增,所以y=f(x)-x2在[0,1)上单调递减.所以
即解得1<a≤.
所以g(a)=()a的取值范围是[,).
- 0 -
教学课时安排
1、上课时间:_________________.
2、课时安排:_________________.
3、上课班级___________________.
学科目标要求
1.理解并掌握幂、指数、对数函数的图象问题;
2.会利用幂、指数、对数函数的性质比较大小;
3.理解并掌握幂、指数、对数函数的性质应用;
4.解决一些抽象函数应用问题.
本节重点难点
重点:幂、指数、对数函数的性质应用;
难点:抽象函数应用问题.
学科素养目标
指数函数、对数函数、幂函数是与现实世界的密切联系的函数模型,是体验函数模型运用过程和方法的重要载体.通过学习,进一步体会函数在数学和其他学科中的重要性,初步运用函数思想理解和处理现实生活和社会中的简单问题,利用函数的性质求方程的近似解,体会函数与方程的有机联系.
在学习基本初等函数I及其应用的过程中,要通过对具体数式的分析,使学生体会分数指数幂、对数的概念和意义,掌握有理指数幂、对数的运算性质,了解并掌握指数函数、对数函数、幂函数的概念、图象和性质;知道指数函数、对数函数、幂函数是描述客观世界变化规律的重要数学模型.
通过函数的应用,了解函数与方程之间的关系,体会二分法求一些简单方程的近似解的方法,尽管这个解也许不准确,但可以通过有效的方法控制精确度;通过数据拟合,体会到现代信息技术是数学课程的一个重要部分;会利用函数知识分析问题、解决问题,能准确、清晰、有条理地表述问题以及问题的解决过程,使学生明白函数与方程是研究事物变化的重要工具,逐步形成利用运动、变化的观点观察事物的理性思维能力、辩证思维能力、分析问题和解决问题的能力,以及数学表达、交流的能力,进一步培养学生的创新意识与探究能力、数学建模能力和实践能力.
知识结构简图
教学过程赏析
基础知识积累
1.常见幂函数的图象与性质
解析式 y=x y=x2 y=x3
图象
定义域 R R R _______ ________
值域 R _______ R ________ _________
奇偶性 ______函数 _____函数 ______函数 _____函数 ________ 函数
解析式 y=x y=x2 y=x3
增区间 _____ _____ _____ 无 ______
减区间 无 _______ 无 _______,_ _________ 无
定点 幂函数的图象均过定点_________
(1)本质:幂函数的图象是函数的图形表示,幂函数的性质是根据函数图象总结得到的.
(2)应用:①求定义域;②求值域;③比较大小;④求单调区间.
2. 指数函数y=ax(a>0,a≠1)的图象与性质
a>1 0
性质 (1)定义域:________
(2)值域: _________
(3)图象过定点_______,图象在x轴上方
a>1 0
注意:在同一坐标系中有多个指数函数图象时,图象的相对位置与底数的大小有如下关系:
①在y轴右侧,图象从上到下相应的底数由大变小;
②在y轴左侧,图象从下到上相应的底数由大变小,即无论在y轴的左侧还是右侧,底数按逆时针方向变大.这一性质可通过令x=1时,y的取值去理解.如图所示:
3. 对数函数的图象与性质
a>1 0
性质 定义域: ____________
值域:______________
a>1 0
在(0,+∞)上是增函数;当0
(1)对数函数单调性的记忆口诀:
对数增减有思路,函数图象看底数;
底数要求大于0,但等于1却不行;
底数若是大于1,图象从左往右增;
底数0到1之间,图象从左往右减;
无论函数增和减,图象都过(1,0)点.
(2)底数对函数图象的影响
对数函数的图象如图所示,可得如下规律:
(ⅰ)与的图象关于x轴对称.
(ⅱ)函数的底数a的变化对图象的影响:
①上下比较:在直线x=1的右侧,当a>1时,底数越大图象越靠近x轴;当0
②左右比较:交点(图象与y=1的交点)的横坐标越大,对应的对数函数的底数a越
大.
【课堂题组训练】
题1. 已知幂函数y=f(x)的图象经过点(-2,-),则满足f(x)=27的x的值为( )
A.3 B. C.27 D.
题2.已知log2x=log3y=log5z>1,则,,的大小排序为( )
A.<< B.<<
C.<< D.<<
题3.已知f(x)=lg (e|x|+2),a=20.3,b=log32,c=log2,则f(a),f(b),f(c)的大小关系为( )
A.f(b)>f(a)>f(c)
B.f(c)>f(a)>f(b)
C.f(a)>f(b)>f(c)
D.f(c)>f(b)>f(a)
题4.函数f(x)=ax2+2x+1与g(x)=xa在同一坐标系中的图象不可能为( )
题5.已知实数a,b满足等式2a=3b,下列关系式中不可能成立的是( )
A.0<b<a B.a<b<0
C.b<a<0 D.a=b
题6.下列说法中错误的个数是( )
①幂函数的图象不过第四象限;
②y=x0的图象是一条直线;
③若函数y=的定义域是,则它的值域是;
④若函数y=x2的值域是,则它的定义域一定是.
A.1 B.2 C.3 D.4
题7.已知f(x)=3x-,若f(m)+f(n)>0,则( )
A.m+n>0 B.m+n<0
C.m-n>0 D.m-n<0
题8.对于函数f(x),若在定义域内存在实数x0满足f(-x0)=-f(x0),则称函数f(x)为“倒戈函数”.设f(x)=3x+m-1(m∈R,m≠0)是定义在[-1,1]上的“倒戈函数”,则实数m的取值范围是( )
A.[-,0) B.[-,-]
C.[-,0] D.(-∞,0)
题9(多选题).已知幂函数f(x)的图象经过(27,),则幂函数f(x)具有的性质是( )
A.在其定义域上为增函数
B.在(0,+∞)上单调递减
C.奇函数
D.定义域为R
题10(多选题).已知函数f(x)=log3在区间(-3,3]上单调递减,则实数a的可取值是( )
A.-1 B.-3 C.0 D.5
题11(多选题).行列式作为基本的数学工具,有着重要的应用,行列式=ad-bc,则下列说法正确的是( )
A.函数f(x)=的值域为[-7,+∞)
B.不等式≥0的解集为[1,+∞)
C.行列式=0是“a=c=0或b=d=0”的必要不充分条件
D.若f(x)=为奇函数,则fi(x)(i=1,2,3,4)均为奇函数
题12(多选题).已知函数f(x)=,g(x)=lg (-x),则( )
A.函数f(x)为偶函数
B.函数g(x)为奇函数
C.函数F(x)=f(x)+g(x)在区间[-1,1]上的最大值与最小值之和为0
D.设F(x)=f(x)+g(x),则F(2a)+F(-1-a)<0的解集为(1,+∞)
题13(多选题).设f(x)=,x∈R,则f(x)是 ( )
A.奇函数且在(-∞,0)上是增函数 B.偶函数且在(-∞,0)上是增函数
C.奇函数且在(0,+∞)上是减函数 D.偶函数且在(0,+∞)上是减函数
题14(多选题).若函数f(x)=ex-e2-x,则下列叙述正确的是 ( )
A.f(x)在(-∞,+∞)上单调递增 B.f(x)的值域为(0,+∞)
C.y=f(x)的图象关于直线x=1对称 D.y=f(x)的图象关于点(1,0)对称
题15(多选题).已知函数f(x)=下列结论正确的是 ( )
A.若f(a)=1,则a=3 B.f=2 020
C.若f(a)≥2,则a≤-1或a≥5 D.若方程f(x)=k有两个不同的实数根,则k>
题16.函数y=+的定义域为____________.
题17.已知125x=12.5y=1 000,则=________.
题18.f(x)=x-x,则满足f(x)>0的x的取值范围为____________.
题19.已知函数y=()mt-7(m为常数),当t=4时,y=64,若y≤,则实数t的取值范围为__________.
题20.已知函数f(x)=2x-.
(1)若f(x)=2,求2x的值;
(2)若2tf(2t)+mf(t)≥0,对于任意t∈[1,2]恒成立,求实数m的取值范围.
题21.已知f(x)是定义在R上的偶函数,且x≤0时,f(x)=log (-x+1).
(1)求函数f(x)的解析式;
(2)若f(a-1)<-1,求实数a的取值范围.
题22.已知函数f(x)=|log2x|.
(1)若x1<x2,且f(x1)=f(x2),求证:+++>3;
(2)解不等式:f(f(x))>1.
题23.已知函数f(x)是偶函数,且当x≥0时,f(x)=loga(3-ax)(a>0,且a≠1).
(1)求x<0时f(x)的解析式;
(2)在①f(x)在(1,4)上单调递增,②在区间(-1,1)上恒有f(x)≥x2这两个条件中任选一个补充到本题中,求g(a)=()a的取值范围.
注:如果选择多个条件分别解答,按第一个解答计分.
编号:037 课题:§6 幂函数、指数函数和对数函数复习课
教学课时安排
1、上课时间:_________________.
2、课时安排:_________________.
3、上课班级___________________.
学科目标要求
1.理解并掌握幂、指数、对数函数的图象问题;
2.会利用幂、指数、对数函数的性质比较大小;
3.理解并掌握幂、指数、对数函数的性质应用;
4.解决一些抽象函数应用问题.
本节重点难点
重点:幂、指数、对数函数的性质应用;
难点:抽象函数应用问题.
学科素养目标
指数函数、对数函数、幂函数是与现实世界的密切联系的函数模型,是体验函数模型运用过程和方法的重要载体.通过学习,进一步体会函数在数学和其他学科中的重要性,初步运用函数思想理解和处理现实生活和社会中的简单问题,利用函数的性质求方程的近似解,体会函数与方程的有机联系.
在学习基本初等函数I及其应用的过程中,要通过对具体数式的分析,使学生体会分数指数幂、对数的概念和意义,掌握有理指数幂、对数的运算性质,了解并掌握指数函数、对数函数、幂函数的概念、图象和性质;知道指数函数、对数函数、幂函数是描述客观世界变化规律的重要数学模型.
通过函数的应用,了解函数与方程之间的关系,体会二分法求一些简单方程的近似解的方法,尽管这个解也许不准确,但可以通过有效的方法控制精确度;通过数据拟合,体会到现代信息技术是数学课程的一个重要部分;会利用函数知识分析问题、解决问题,能准确、清晰、有条理地表述问题以及问题的解决过程,使学生明白函数与方程是研究事物变化的重要工具,逐步形成利用运动、变化的观点观察事物的理性思维能力、辩证思维能力、分析问题和解决问题的能力,以及数学表达、交流的能力,进一步培养学生的创新意识与探究能力、数学建模能力和实践能力.
知识结构简图
教学过程赏析
基础知识积累
1.常见幂函数的图象与性质
解析式 y=x y=x2 y=x3
图象
定义域 R R R _{x|x≠0}_ __[0,+∞)__
值域 R __[0,+∞)_ R _{y|y≠0}_ __[0,+∞)__
奇偶性 _ 奇__函数 __偶_函数 __奇_函数 _奇__函数 __非奇非偶_ 函数
解析式 y=x y=x2 y=x3
增区间 __ __[0,+∞)_ __ 无 __[0,+∞)__
减区间 无 __(-∞,0)__ 无 __(-∞,0),_ __(0,+∞)__ 无
定点 幂函数的图象均过定点__(1,1)_
(1)本质:幂函数的图象是函数的图形表示,幂函数的性质是根据函数图象总结得到的.
(2)应用:①求定义域;②求值域;③比较大小;④求单调区间.
2. 指数函数y=ax(a>0,a≠1)的图象与性质
a>1 0
性质 (1)定义域:_ _
(2)值域: ___ __
(3)图象过定点__ __,图象在x轴上方
a>1 0
注意:在同一坐标系中有多个指数函数图象时,图象的相对位置与底数的大小有如下关系:
①在y轴右侧,图象从上到下相应的底数由大变小;
②在y轴左侧,图象从下到上相应的底数由大变小,即无论在y轴的左侧还是右侧,底数按逆时针方向变大.这一性质可通过令x=1时,y的取值去理解.如图所示:
3. 对数函数的图象与性质
a>1 0
性质 定义域: ___(0,+∞)_____
值域: ________
a>1 0
在(0,+∞)上是增函数;当0
(1)对数函数单调性的记忆口诀:
对数增减有思路,函数图象看底数;
底数要求大于0,但等于1却不行;
底数若是大于1,图象从左往右增;
底数0到1之间,图象从左往右减;
无论函数增和减,图象都过(1,0)点.
(2)底数对函数图象的影响
对数函数的图象如图所示,可得如下规律:
(ⅰ)与的图象关于x轴对称.
(ⅱ)函数的底数a的变化对图象的影响:
①上下比较:在直线x=1的右侧,当a>1时,底数越大图象越靠近x轴;当0
②左右比较:交点(图象与y=1的交点)的横坐标越大,对应的对数函数的底数a越
大.
【课堂题组训练】
题1. 已知幂函数y=f(x)的图象经过点(-2,-),则满足f(x)=27的x的值为( )
A.3 B. C.27 D.
【解析】选D.因为幂函数y=xα的图象经过点(-2,-),所以(-2)α=-,所以α=-3.
又因为f(x)=27,所以x-3=27,所以x=.
题2.已知log2x=log3y=log5z>1,则,,的大小排序为( )
A.<< B.<<
C.<< D.<<
【解析】选D.由log2x=log3y=log5z>1,
得1-log2x=1-log3y=1-log5z<0,即
log2=log3=log5<0,
可得<<.
题3.已知f(x)=lg (e|x|+2),a=20.3,b=log32,c=log2,则f(a),f(b),f(c)的大小关系为( )
A.f(b)>f(a)>f(c)
B.f(c)>f(a)>f(b)
C.f(a)>f(b)>f(c)
D.f(c)>f(b)>f(a)
【解析】选B.f(-x)=lg (e|-x|+2)=lg (e|x|+2)=f(x),f(x)是偶函数,
x≥0时f(x)=lg (ex+2)是增函数,1<20.3<2,0<log32<1,log2=-2,f(log2)=f(-2)=f(2),
而log32<20.3<2,所以f(log32)<f(20.3)<f(2),即f(b)<f(a)<f(c).
题4.函数f(x)=ax2+2x+1与g(x)=xa在同一坐标系中的图象不可能为( )
【解析】选B.当a=-1时,g(x)=xa为奇函数,定义域为,且在(0,
+∞)上递减,而f(x)=ax2+2x+1开口向下,对称轴为x=->0,
f(0)=1,故A符合,B不符合;
当a=2n(n∈N+)时,g(x)=xa为偶函数,且在(0,+∞)上递增,f(x)=ax2+2x+1开口向上,且对称轴为x=-<0,Δ=4-4a<0,其图象和x轴没有交点,故D符合;
当a=(n∈N+)时,函数g(x)=xa的定义域为[0,+∞),且在[0,+∞)上递增,f(x)=ax2+2x+1开口向上且对称轴为x=-<0,Δ=4-4a>0,图象和x轴有两个交点,故C符合.
题5.已知实数a,b满足等式2a=3b,下列关系式中不可能成立的是( )
A.0<b<a B.a<b<0
C.b<a<0 D.a=b
【解析】选C.作出函数y=2x与函数y=3x的图象,如图,当2a=3b>1时根据图象得0<b<a,故A选项正确,不符合题意;
当2a=3b=1时,根据图象得a=b=0,故D选项正确,不符合题意;
当2a=3b<1时根据图象得a<b<0,故B选项正确,不符合题意;故不可能成立的是b<a<0.
题6.下列说法中错误的个数是( )
①幂函数的图象不过第四象限;
②y=x0的图象是一条直线;
③若函数y=的定义域是,则它的值域是;
④若函数y=x2的值域是,则它的定义域一定是.
A.1 B.2 C.3 D.4
【解析】选C.由幂函数的图象与性质知①正确;
y=x0的图象是直线y=1上去掉点(0,1),②错误;
函数y=的定义域是,则它的值域是,③错误;
若函数y=x2的值域是,则它的定义域也可能是,④错误.
题7.已知f(x)=3x-,若f(m)+f(n)>0,则( )
A.m+n>0 B.m+n<0
C.m-n>0 D.m-n<0
【解析】选A.因为f(x)=3x-,x∈R,所以f(-x)=3-x-=
x-3x=-f(x),所以f(x)是定义域为R的奇函数,且是增函数;又f(m)+f(n)>0,所以f(m)>-f(n)=f(-n),所以m>-n,所以m+n>0.
题8.对于函数f(x),若在定义域内存在实数x0满足f(-x0)=-f(x0),则称函数f(x)为“倒戈函数”.设f(x)=3x+m-1(m∈R,m≠0)是定义在[-1,1]上的“倒戈函数”,则实数m的取值范围是( )
A.[-,0) B.[-,-]
C.[-,0] D.(-∞,0)
【解析】选A.因为f(x)=3x+m-1是定义在[-1,1]上的“倒戈函数,所以存在x0∈[-1,1]满足f(-x0)=-f(x0),所以3+m-1=-3-m+1,
所以2m=-3-3+2,构造函数y=-3-3+2,x0∈[-1,1],
令t=3,t∈[,3],y=--t+2=2-(t+)在[,1]单调递增,
在(1,3]单调递减,所以t=1取得最大值0,t=或t=3取得最小值-,y∈[-,0],
所以-≤2m<0,所以-≤m<0.
题9(多选题).已知幂函数f(x)的图象经过(27,),则幂函数f(x)具有的性质是( )
A.在其定义域上为增函数
B.在(0,+∞)上单调递减
C.奇函数
D.定义域为R
【解析】选BC.设幂函数f(x)=xa,因为幂函数图象过点(27,),所以27a=,所以a=-,所以f(x)=x= (x≠0),所以f(x)定义域为(-∞,0)∪(0,+∞),满足f(-x)=-f(x),是奇函数,值域为(-∞,0)∪(0,+∞),在定义域内不单调,在上单调递减.
题10(多选题).已知函数f(x)=log3在区间(-3,3]上单调递减,则实数a的可取值是( )
A.-1 B.-3 C.0 D.5
【解析】选AC.令u=,由题意可知,u=>0对任意的x∈(-3,3]恒成立,
因为x+3>0,则ax+6>0对任意的x∈(-3,3]恒成立,则,得
-2<a≤2.
因为函数f(x)=log3在区间(-3,3]上单调递减,外层函数y=log3u为增函数,
故内层函数u===a+在区间(-3,3]上为减函数,
所以6-3a>0,可得a<2.综上所述,-2<a<2.
题11(多选题).行列式作为基本的数学工具,有着重要的应用,行列式=ad-bc,则下列说法正确的是( )
A.函数f(x)=的值域为[-7,+∞)
B.不等式≥0的解集为[1,+∞)
C.行列式=0是“a=c=0或b=d=0”的必要不充分条件
D.若f(x)=为奇函数,则fi(x)(i=1,2,3,4)均为奇函数
【解析】选ABC.对于A,f(x)==x(x-2)-6=(x-1)2-7≥-7,故f(x)的值域为[-7,+∞),故A正确;
对于B,≥0 2x-1·4x-2×2≥0 23x-1≥22,解得x≥1,故B正确;
对于C,当“a=c=0或b=d=0”时,可得=0;而当=0时,取a=b=c=d=1,可得“a=c=0或b=d=0”不成立,故C正确;
对于D,若f(x)=为奇函数,取fi(x)(i=1,2,3,4)=x2,可得f(x)=0为R上的奇函数,故D错误.
题12(多选题).已知函数f(x)=,g(x)=lg (-x),则( )
A.函数f(x)为偶函数
B.函数g(x)为奇函数
C.函数F(x)=f(x)+g(x)在区间[-1,1]上的最大值与最小值之和为0
D.设F(x)=f(x)+g(x),则F(2a)+F(-1-a)<0的解集为(1,+∞)
【解析】选BCD.f(x)=,定义域为R,
f(-x)==-=-f(x),
则f(x)为奇函数,故A错误;
g(x)=lg (-x),定义域为R,
g(-x)=lg (-(-x))
=-lg (-x)=-g(x),
则g(x)为奇函数,故B正确;
对于C:F(x)=f(x)+g(x),f(x),g(x)都为奇函数,则F(x)=f(x)+g(x)为奇函数,
F(x)=f(x)+g(x)在区间[-1,1]上的最大值与最小值互为相反数,必有F(x)在区间[-1,1]上的最大值与最小值之和为0,故C正确;
f(x)==-()=-1,则f(x)在R上为减函数,
g(x)=lg (-x)=lg ,
则g(x)在R上为减函数,则F(x)=f(x)+g(x)在R上为减函数,若F(2a)+F(-1-a)<0,即F(2a)<F(1+a),则必有2a>1+a,解得a>1,
即F(2a)+F(-1-a)<0的解集为(1,+∞),故D正确.
题13(多选题).设f(x)=,x∈R,则f(x)是 ( )
A.奇函数且在(-∞,0)上是增函数 B.偶函数且在(-∞,0)上是增函数
C.奇函数且在(0,+∞)上是减函数 D.偶函数且在(0,+∞)上是减函数
【解析】选BD.依题意,得f(-x)===f(x),所以f(x)是偶函数.当x>0时,f(x)==,该指数函数是减函数;当x<0时,f(x)===2x,该指数函数是增函数.
题14(多选题).若函数f(x)=ex-e2-x,则下列叙述正确的是 ( )
A.f(x)在(-∞,+∞)上单调递增 B.f(x)的值域为(0,+∞)
C.y=f(x)的图象关于直线x=1对称 D.y=f(x)的图象关于点(1,0)对称
【解析】选AD.对于A,因为y=ex在(-∞,+∞)上单调递增,y=-e2-x在(-∞,+∞)上单调递增,所以f(x)在(-∞,+∞)上单调递增,故A正确;对于B,f(0)=1-e2<0,故B错误;对于C,f(0)=1-e2,f(2)=e2-1,f(0)≠f(2),所以y=f(x)的图象不关于直线x=1对称,故C错误;对于D,因为f(1+x)=e1+x-e1-x,f(1-x)=e1-x-e1+x,所以f(1+x)+f(1-x)=0,则y=f(x)的图象关于点(1,0)对称,故D正确.
题15(多选题).已知函数f(x)=下列结论正确的是 ( )
A.若f(a)=1,则a=3 B.f=2 020
C.若f(a)≥2,则a≤-1或a≥5 D.若方程f(x)=k有两个不同的实数根,则k>
【解析】选BC.对于A:由f(a)=1,
得 或 解得a=3或a=0,故A错误;
对于B:f=log2=log2=,因为<0,
所以f=f()==2 020,故B正确;
对于C:由f(a)≥2,得 或解得a≥5或a≤-1,故C正确;
对于D:作出f(x)的图象,如图所示:
又f(1)=,结合图象可得f(x)=k有两个不同的实数根,即y=f(x)的图象与y=k的图象有两个交点,所以k≥,故D错误.
题16.函数y=+的定义域为____________.
【解析】由题意,,得,
所以-2≤x<1.
答案:[-2,1)
题17.已知125x=12.5y=1 000,则=________.
【解析】因为125x=12.5y=1 000,
所以x=log125 1 000,y=log12.5 1 000,
=-=log1 000 125-log1 00012.5
=log1 000=log1 000 10=.
答案:
题18.f(x)=x-x,则满足f(x)>0的x的取值范围为____________.
【解析】因为f(x)=x-x>0,所以x>x.
在同一坐标系中作出y=x,y=x的图象,如图所示:
结合幂函数图象可得x∈(-∞,0)∪(1,+∞).
答案:(-∞,0)∪(1,+∞)
题19.已知函数y=()mt-7(m为常数),当t=4时,y=64,若y≤,则实数t的取值范围为__________.
【解析】将t=4,y=64代入y=()mt-7,
可得64=()4m-7,解得m=,所以y=().由()≤,得t-7≥1,解得t≥32.故实数t的取值范围是[32,+∞).
答案:[32,+∞)
题20.已知函数f(x)=2x-.
(1)若f(x)=2,求2x的值;
(2)若2tf(2t)+mf(t)≥0,对于任意t∈[1,2]恒成立,求实数m的取值范围.
【解析】(1)当x<0时,f(x)=0≠2,舍去;
当x≥0时,f(x)=2x-=2,
即(2x)2-2·2x-1=0,2x>0.
解得2x=1+.
(2)当t∈[1,2]时,2tf(2t)+mf(t)≥0,即2t+m(2t-)≥0,
即m(22t-1)≥-(24t-1),因为22t-1>0,所以m≥-(22t+1).
由t∈[1,2],所以-(22t+1)∈[-17,-5].
故m的取值范围是[-5,+∞).
题21.已知f(x)是定义在R上的偶函数,且x≤0时,f(x)=log (-x+1).
(1)求函数f(x)的解析式;
(2)若f(a-1)<-1,求实数a的取值范围.
【解析】(1)令x>0,则-x<0,
f(-x)=log (x+1)=f(x),
所以x>0时,f(x)=log (x+1),
则f(x)=
(2)因为f(x)=log (-x+1)在(-∞,0]上为增函数,所以f(x)在(0,+∞)上为减函数.
因为f(a-1)<-1=f(1),所以|a-1|>1,解得a>2或a<0.
故实数a的取值范围为(-∞,0)∪(2,+∞).
题22.已知函数f(x)=|log2x|.
(1)若x1<x2,且f(x1)=f(x2),求证:+++>3;
(2)解不等式:f(f(x))>1.
【解析】(1)f(x)=|log2x|=作出f(x)=|log2x|的图象如图所示:
由f(x1)=f(x2)可得-log2x1=log2x2,即log2x1+log2x2=0,所以log2(x1x2)=0,可得x1x2=1且x1≠1,
所以+=+=1,而+=+x1≥2=2,当且仅当x1=1时取等号,而x1≠1,所以+>2.
综上:+++>3.
(2)令f(x)=t,由f(t)>1即f(t)=|log2t|>1,可得log2t>1或log2t<-1,
所以0<t<或t>2,所以0<f(x)<或f(x)>2,即0<|log2x|<或|log2x|>2,
由0<|log2x|<,可得-<log2x<且log2x≠0,即log2<log2x<=log2,解得:<x<且x≠1,由|log2x|>2可得log2x>2=log24或log2x<-2=log2,解得0<x<或x>4,
综上:f(f(x))>1的解集为(0,)∪(,1)∪(1,)∪(4,+∞).
题23.已知函数f(x)是偶函数,且当x≥0时,f(x)=loga(3-ax)(a>0,且a≠1).
(1)求x<0时f(x)的解析式;
(2)在①f(x)在(1,4)上单调递增,②在区间(-1,1)上恒有f(x)≥x2这两个条件中任选一个补充到本题中,求g(a)=()a的取值范围.
注:如果选择多个条件分别解答,按第一个解答计分.
【解析】(1)当x<0时,-x>0,因为f(x)是偶函数,所以f(x)=f(-x)=loga(3+ax).所以当x<0时,f(x)=loga(3+ax).
(2)选条件①:由于f(x)在(1,4)上单调递增,所以a>1不合题意.
所以解得0<a≤,
所以g(a)=()a的取值范围是[,1).
选条件②:当0<a<1时,f(0)=loga3<0,显然不满足题意;
当a>1时,因为f(x)与y=x2都是偶函数,所以只需考虑x∈[0,1)时,f(x)≥x2恒成立即可.
由复合函数的单调性可知,函数f(x)在[0,1)上单调递减,而y=x2在[0,1)上单调递增,所以y=f(x)-x2在[0,1)上单调递减.所以
即解得1<a≤.
所以g(a)=()a的取值范围是[,).
- 0 -
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
