切线的判定

课件29张PPT。课前练习：
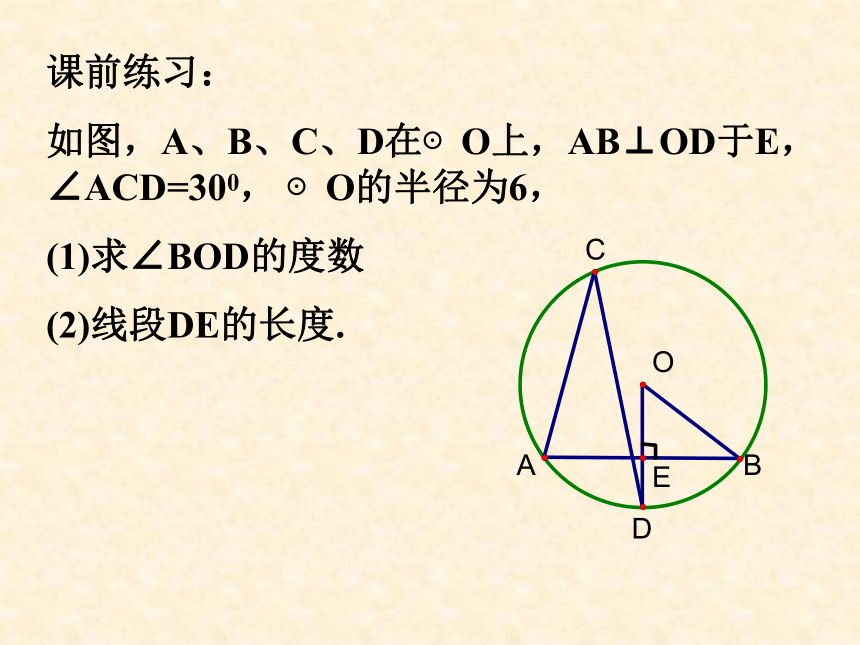
如图，A、B、C、D在⊙O上，AB⊥OD于E，∠ACD=300， ⊙O的半径为6，
(1)求∠BOD的度数
(2)线段DE的长度.24.2.2
直线与圆的位置关系
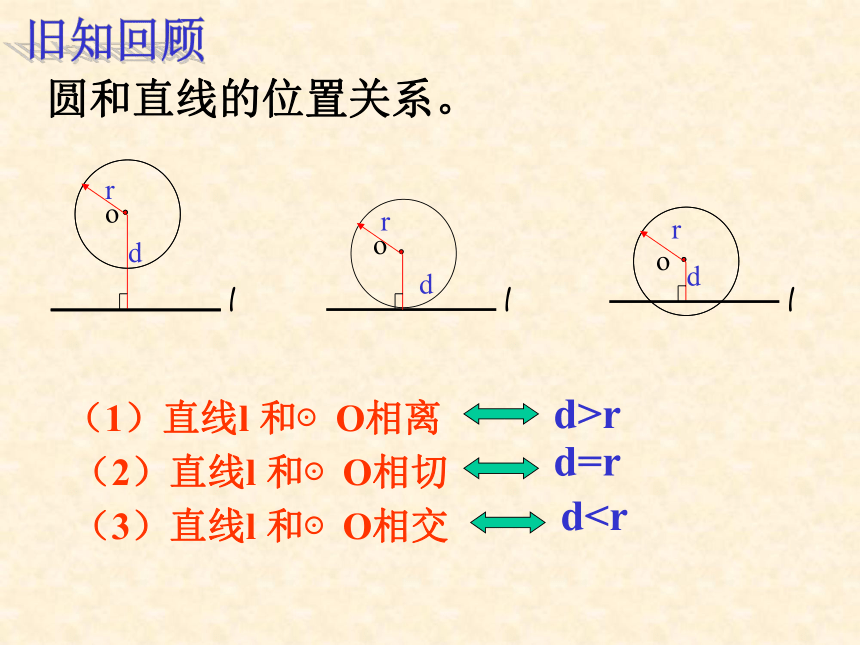
(2)（2）直线l 和⊙O相切圆和直线的位置关系。 （1）直线l 和⊙O相离（3）直线l 和⊙O相交d>rd=rd⊙O有什么位置关系?
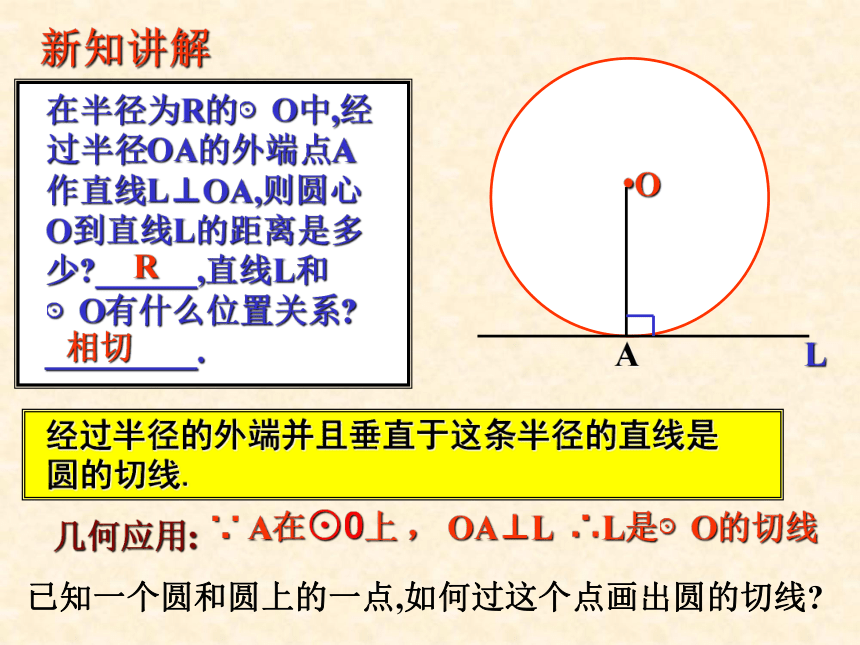
_________.新知讲解.OAR相切L经过半径的外端并且垂直于这条半径的直线是
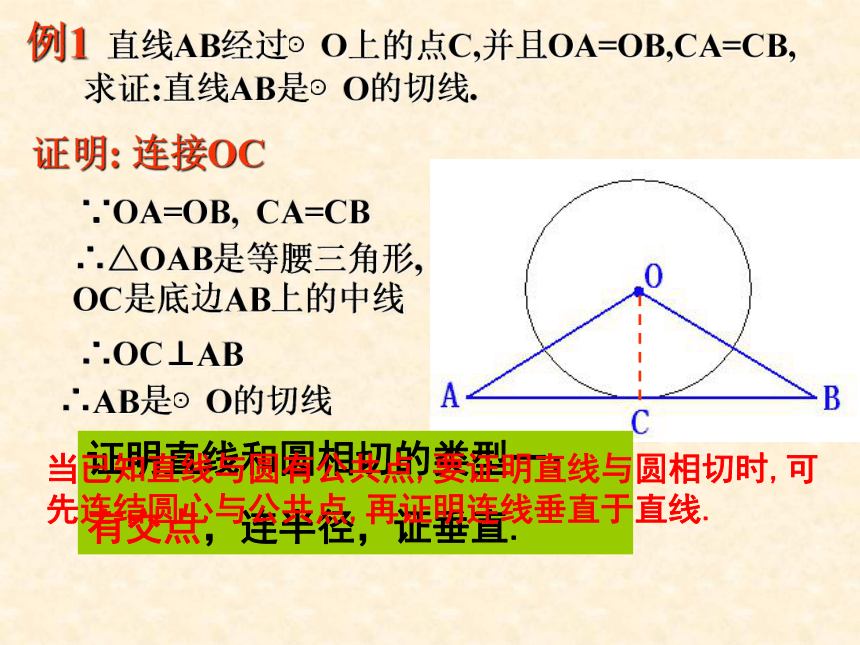
圆的切线.几何应用: ∵ A在⊙O上 ， OA⊥L ∴L是⊙O的切线已知一个圆和圆上的一点,如何过这个点画出圆的切线?例1 直线AB经过⊙O上的点C,并且OA=OB,CA=CB,
求证:直线AB是⊙O的切线.证明: 连接OC∵OA=OB, CA=CB∴△OAB是等腰三角形,
OC是底边AB上的中线
∴OC⊥AB∴AB是⊙O的切线证明直线和圆相切的类型一：
有交点，连半径，证垂直.当已知直线与圆有公共点,要证明直线与圆相切时,可先连结圆心与公共点,再证明连线垂直于直线.练习1：如图A是⊙O外的一点，AO的延长线交⊙O于C，直线AB经过⊙O上一点B，且AB＝BC，∠C＝30°。求证：直线AB是⊙O的切线证明：连结OB∵OB=OC,AB=BC,∠C=30°
∴∠OBC=∠C=∠A=30°
∴∠AOB=∠C+∠OBC=60°
∴∠ABO=180°－(∠AOB+∠A)=90°
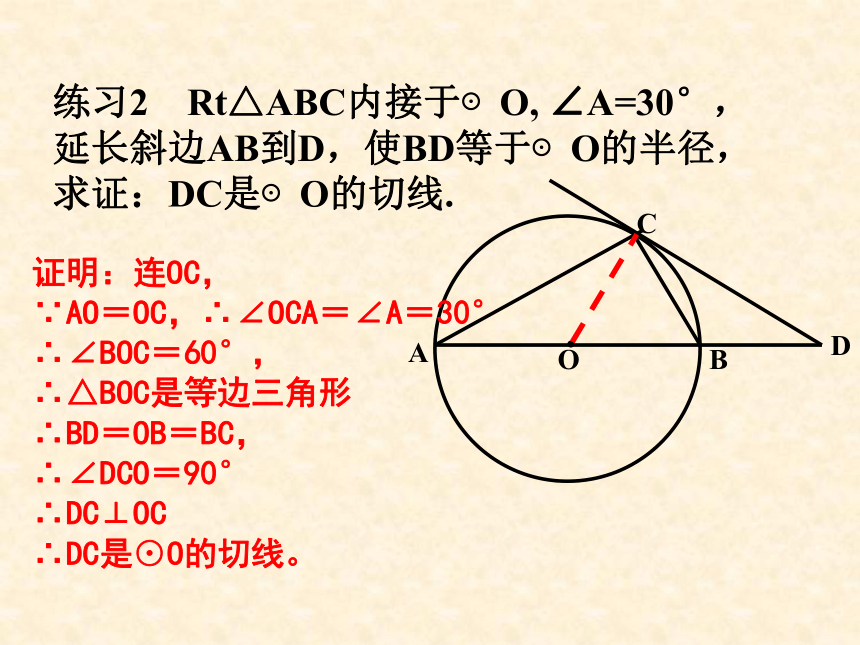
∴ AB是⊙O的切线练习2 Rt△ABC内接于⊙O, ∠A=30°，延长斜边AB到D，使BD等于⊙O的半径，求证：DC是⊙O的切线.
证明：连OC，
∵AO＝OC，∴∠OCA＝∠A＝30°∴∠BOC＝60°，
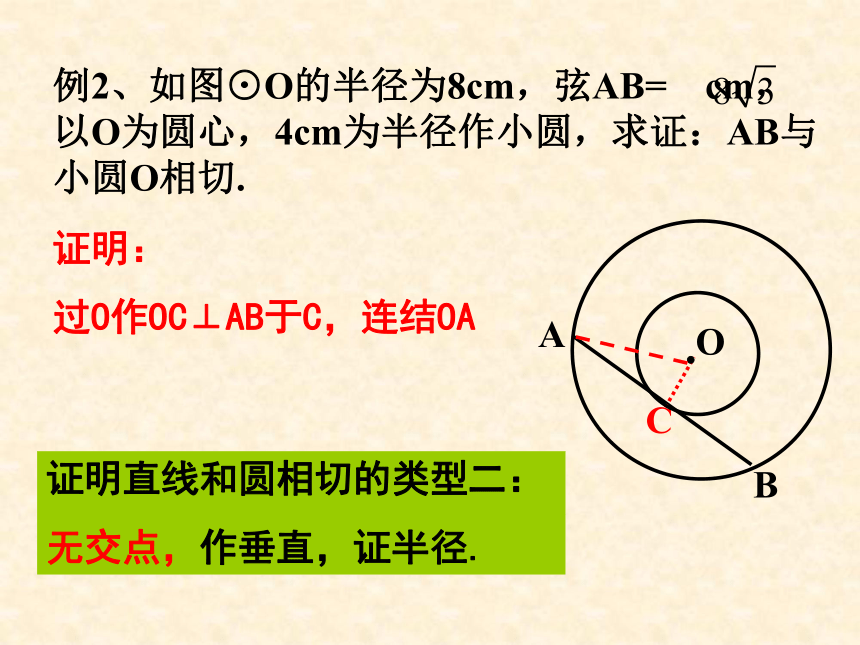
∴△BOC是等边三角形∴BD＝OB＝BC，∴∠DCO＝90°∴DC⊥OC∴DC是⊙O的切线。例2、如图⊙O的半径为8cm，弦AB= cm，以O为圆心，4cm为半径作小圆，求证：AB与小圆O相切.证明：
过O作OC⊥AB于C，连结OA证明直线和圆相切的类型二：
无交点，作垂直，证半径.1、定义法：和圆有且只有一个公共点的直线是圆的切线。
2、数量法（d=r）：和圆心距离等于半径的直线是圆的切线。
3、判定定理：经过半径外端且垂直于这条半径的直线是圆的切线。证明直线与圆相切有如下三种途径:无交点，作垂直，证半径.有交点，连半径，证垂直.证明直线和圆相切的两种思路：练习4、已知：在△ABC中，AB＝AC，以AB为直径作⊙O交BC于D，DE⊥AC于E，如图，
求证：DE是⊙O的切线。　　　　练习5.已知:三角形ABC内接于⊙O,过点A作直线EF.
(1)图甲,AB为直径,要使得EF是⊙O切线,还需添加的条件
(只需写出三种情况)①___________②_____________
③______________.
(2)图乙, AB为非直径的弦,∠CAE=∠B.求证:EF是⊙O的
切线.∠CAE=∠BAB⊥FE∠BAC+∠CAE=90°H弧AC所对的弦切角 EAC等于弧AC所对的圆周角 ABC 5.小红家的锅盖坏了,为了配一个锅盖,需要测量锅盖的
直径(锅边所形成的圆的直径),而小红家只有一把长20cm
的直尺,根本不够长,怎么办呢?小红想了想,采取以下方
法:首先把锅平放到墙根,锅边刚好靠到两墙,用直尺紧贴
墙面量得MA的长,即可求出墙的直径,请你利用图乙,说
明她这样做的道理.练习2、如图,AB是⊙O的直径,点D在AB的延长线 上，BD=OB，点C在圆上，∠CAB=300.
求证:DC是⊙O的切线.证明：连OC、BC，
∵AO＝OC，∴∠OCA＝∠A＝30°∴∠BOC＝60°，
∴△BOC是等边三角形∴BD＝OB＝BC，∠D＝∠BCD＝30°∴∠DCO＝90°∴DC⊥OC∴DC是⊙O的切线。１、切线和圆只有一个公共点。２、切线和圆心的距离等于半径。３、切线垂直于过切点的半径。４、经过圆心垂直于切线的直线必过切点。５、经过切点垂直于切线的直线必过圆心。切线的性质：切线的性质３、４、５可归纳为：已知直线满足a、过圆心，b、过切点，c、垂直于切线中任意两个，便得到第三个结论。1.如图 AB是⊙O的直径,∠ABT=45°AT=AB,求证AT 是⊙O的切线.证明:∵ ∠ABT = 45°，∴ ∠ATB = ∠ABT=45 °.∴ ∠TAB = 180°－∠ATB－∠ABT = 90°.∴ TA⊥OA.∴ AT是⊙O的切线.∵ OA是⊙O的半径，活动4(
如图,△ABC内接于⊙O，∠B＝∠C，小圆与AB相切，求证：AC为小圆的切线。　　　　　　　　　　　　　　　 ?????????????????????　　　　　　　　　　　　　　　证明：作OE⊥AC于E，OD⊥AB于D
　设小圆的半径为r。 　∵∠B＝∠C，∴AB＝AC，
∴OD＝OE 又∵AB与大圆相切，
∴OD＝r，∴OE＝r 　故由切线判定定理知，AC为小圆切线。
课后作业:1．已知：在△ABC中，AB＝AC，以AB为直径作⊙O交BC于D，DE⊥AC于E， 　　　　 如图，求证：DE是⊙O的切线。　　　　　　　　　　动画演示 　　　　 分析：因为DE经过⊙O上的点D，所以要证明DE为切线，可连结OD， 　　　　 再证明DE⊥OD。 　　　　　　　　　　　　　　　 ??????????????????????　　　　　　　　　　　　　　　　　　　　　2．如图(10)，已知在△ABC中，AD⊥BC于D，AD＝ ?BC，E和F分别为AB和 AC的中点，EF与AD交于G，以EF为直径作⊙O，求证：⊙O与BC相切。
分析：要证明以EF为直径的⊙O与BC相切，只要过O作OH⊥BC于H，证 明OH等于直径EF的一半。　　　　　　　　　　　　　　 动画演示　　　　　　　　　　　　　　　　 3．如图，△ABC内接于⊙O，P、B、C在一直线上，且PA2＝PB·PC， 求证：PA是⊙O的切线。 　　　　 分析：∵PA过⊙O上一点A，要证PA为切线，只要证PA⊥AO，为此，作 　　　　 直径AD，并连结CD，只要证PA⊥AD即可。 　　　　　　　　　　　　　 ???????????????????????????　　　　　　　　　　　　　　　　　　 练习1、已知：直线AB经过⊙O上的点C，并且OA=OB,CA=CB.
求证：直线AB是⊙O的切线。OABC分析： 欲证AB是⊙O的切线，由于AB过圆上点C，若连结OC,则AB过半径OC的外端，只需证明OC⊥AB .练习1、已知：直线AB经过⊙O上的
点C，并且OA=OB,CA=CB.
求证：直线AB是⊙O的切线。OABC证明：如图，连结OC.
∵ OA=OB,CA=CB
∴ OC是等腰△OAB
底边BC上的中线
∴ OC⊥AB
又AB过半径OC的外端
∴ AB是⊙O的切线练习1：如图，AB是⊙O的直径，∠ABT=45°,
AT=AB。 求证：AT是⊙O的切线。BAOTC练习2：AB是⊙O的直径，点D在AB的延长线上
BD=OB,点C在圆上，∠CAB=30°。
求证：DC是⊙O的切线。CDBAO123OBACD例 如图，AB为⊙O的直径， C为⊙O上一点，AD和过C点的切线互相垂直，垂足为D.
求证：AC平分∠DAB.CD是 ⊙O的切线OC⊥CDAD⊥CDOC∥AD∠1=∠2OC = OA∠1=∠3∠1=∠3AC平分∠DAB证明：如图，连接OC.DCBOA练习3
如图，在⊙O中，AB为直径， AD为弦， 过B点的切线与AD的延长线交于点C，且AD=DC
求∠ABD的度数.解： AB为直径BC为切线∠ABC=90°△ABC为直角三角形AD=DC∠ADB=90°AD=DB∠ADC=90°△ABD为等腰直角三角形∠ABD=45°求证：经过直径两端点的切线互相平行练习4 已知：如图，AB 是⊙O的直径，AC、BD是⊙O的切线.
证明：如图，AB 是⊙O的直径AC、BD是⊙O的切线AB⊥ACAB⊥BDAC∥BD求证: AC∥BD.OAL思考将上页思考中的问题
反过来,如果L是⊙O
的切线,切点为A,那么
半径OA与直线L是不
是一定垂直呢?一定垂直切线的性质定理:圆的切线垂直于过切点的半径练习 P103. 1. 2 　例3．已知：如图,⊙O的半径为4cm，OA⊥OB，
OC⊥AB于C，OB＝4 cm，OA＝2 cm，
求证：AB与⊙O相切。证明：∵OA⊥OB，OC⊥AB
∴△AOB是直角三角形 又∵OA＝2 cm，OB＝4 cm
∴AB＝10 根据三角形面积公式有：AB·OC＝OA·OB ∴OC＝ 4(cm)，OC是⊙O的半径。 直线AB经过半径OC的外端C，并且垂直于
半径OC所 以AB与 ⊙O相切。 　题目中“垂直”已有，只需证“距离等于半径”，即可得直线与圆相切。练习2
如图的两个圆是以O为圆心的同心圆，大圆的弦AB是小圆的切线， C为切点.求证：C是AB的中点.CABO证明：如图，∴ C是AB的中点.AC=BC根据垂径定理，得OC⊥AB连接OC, 则