1.1.2探索勾股定理(2) 导学案 (无答案)2023—2024学年北师大版数学八年级上册
文档属性
| 名称 | 1.1.2探索勾股定理(2) 导学案 (无答案)2023—2024学年北师大版数学八年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 170.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-14 00:00:00 | ||
图片预览

文档简介
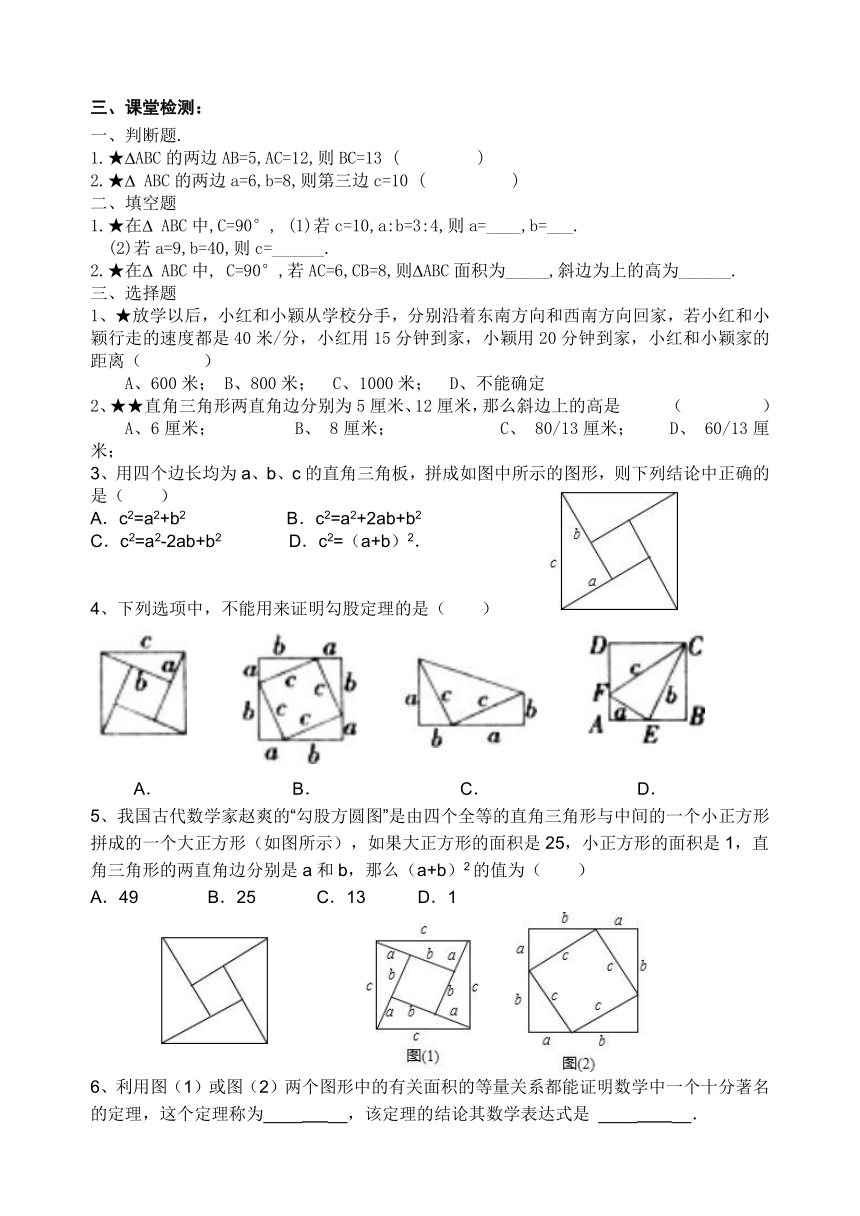
1.1.2探索勾股定理(2)
执笔: 审核:初 二备课组 课型:新授 授课时间: 第 (1) 周
【学习目标】1、 经历运用拼图的方法说明勾股定理的过程,在数学活动中发展学生的探究意识和合作交流的习惯。
2、 掌握勾股定理和他的简单应用
【学习重点】能熟练运用拼图的方法证明勾股定理。
【学习难点】用面积法证勾股定理。
一、预习导学:
1、补充完全平方公式:(a+b)2 =
2、如图,在Rt ABC中,∠B=900,a、b、c的关系为:
面积表示为
二、探究活动:验证勾股定理
在右图中,四边形APQC,四边形CDEF,四边形BCMN,四边形ABGH为正方形, ABC
BGF、 GHE、 HAD为全等的直角三角形,三边分别为a、b、c,则正方形CDEF的边长用a、b表示为:
面积用a、b表示为
还可用a、b、c表示为:
由此可得等式:
从而推导出: 定理的关系式为:
拼图验证. 准备的四个全等的直角三角形拼出正方形.
思考1: 你能由图1表示大正方形的面积吗?
(
a
a
a
b
b
c
c
) (
22
)能用两种方法吗?能由此得到勾股定理吗?
(
图
1
)
(
图
3
) (
图
2
)
2:你能由图2表示大正方形的面积吗?能用两种方法吗?能由此得到勾股定理吗?
3、请利用图3验证勾股定理
三、课堂检测:
一、判断题.
1.★ABC的两边AB=5,AC=12,则BC=13 ( )
2.★ ABC的两边a=6,b=8,则第三边c=10 ( )
二、填空题
1.★在 ABC中,C=90°, (1)若c=10,a:b=3:4,则a=____,b=___.
(2)若a=9,b=40,则c=______.
★在 ABC中, C=90°,若AC=6,CB=8,则ABC面积为_____,斜边为上的高为______.
三、选择题
1、★放学以后,小红和小颖从学校分手,分别沿着东南方向和西南方向回家,若小红和小颖行走的速度都是40米/分,小红用15分钟到家,小颖用20分钟到家,小红和小颖家的距离( )
A、600米; B、800米; C、1000米; D、不能确定
2、★★直角三角形两直角边分别为5厘米、12厘米,那么斜边上的高是 ( )
A、6厘米; B、 8厘米; C、 80/13厘米; D、 60/13厘米;
3、用四个边长均为a、b、c的直角三角板,拼成如图中所示的图形,则下列结论中正确的是( )
A.c2=a2+b2 B.c2=a2+2ab+b2
C.c2=a2-2ab+b2 D.c2=(a+b)2.
4、下列选项中,不能用来证明勾股定理的是( )
A. B. C. D.
5、我国古代数学家赵爽的“勾股方圆图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示),如果大正方形的面积是25,小正方形的面积是1,直角三角形的两直角边分别是a和b,那么(a+b)2的值为( )
A.49 B.25 C.13 D.1
6、利用图(1)或图(2)两个图形中的有关面积的等量关系都能证明数学中一个十分著名的定理,这个定理称为____ __,该定理的结论其数学表达式是 ____ __.
四:归纳总结:
验证勾股定理用的是什么方法?
五、课外作业:
1.★如图,是某沿江地区交通平面图,为了加快经济发展,该地区拟修建一条连接M,O,Q三城市的沿江高速的建设成本是100万元∕千米,该沿江高速的造价是多少?
2.★如图,从电线杆离地面6米处向地面拉一条长10米的缆绳,
这条缆绳在地面的固定点距离电线杆底部有多远?
3.★一直角三角形的斜边比直角边大2,另一直角边长为6,则斜边长为
★直角三角形两直角边分别为5厘米、12厘米,那么斜边上的高是
5.★直角三角形的三边长为连续偶数,则其周长为
6.★以直角三角形的两直角边为边长向外作正方形,所作的正方形的面积分别为9和16,则直角三角形的斜边长为
7.★★如图,是一块直角三角形纸片,两直角边AC=6㎝,BC=8㎝,现将ABC沿直线AD折叠,使AC落在斜边AB上,且与AE重合,求CD的长
8、如图1-4,一架梯子长25米,斜靠在一面墙上,梯子顶端离地面15米,要使梯子顶端离地24米,则梯子的底部在水平方向上应滑动多少米?
9★★★如图7,矩形纸片ABCD的边AB=10,BC=6,E为BC上一点,将矩形纸片沿AE折叠,点B恰好落在CD边上的点G处,求BE的长
执笔: 审核:初 二备课组 课型:新授 授课时间: 第 (1) 周
【学习目标】1、 经历运用拼图的方法说明勾股定理的过程,在数学活动中发展学生的探究意识和合作交流的习惯。
2、 掌握勾股定理和他的简单应用
【学习重点】能熟练运用拼图的方法证明勾股定理。
【学习难点】用面积法证勾股定理。
一、预习导学:
1、补充完全平方公式:(a+b)2 =
2、如图,在Rt ABC中,∠B=900,a、b、c的关系为:
面积表示为
二、探究活动:验证勾股定理
在右图中,四边形APQC,四边形CDEF,四边形BCMN,四边形ABGH为正方形, ABC
BGF、 GHE、 HAD为全等的直角三角形,三边分别为a、b、c,则正方形CDEF的边长用a、b表示为:
面积用a、b表示为
还可用a、b、c表示为:
由此可得等式:
从而推导出: 定理的关系式为:
拼图验证. 准备的四个全等的直角三角形拼出正方形.
思考1: 你能由图1表示大正方形的面积吗?
(
a
a
a
b
b
c
c
) (
22
)能用两种方法吗?能由此得到勾股定理吗?
(
图
1
)
(
图
3
) (
图
2
)
2:你能由图2表示大正方形的面积吗?能用两种方法吗?能由此得到勾股定理吗?
3、请利用图3验证勾股定理
三、课堂检测:
一、判断题.
1.★ABC的两边AB=5,AC=12,则BC=13 ( )
2.★ ABC的两边a=6,b=8,则第三边c=10 ( )
二、填空题
1.★在 ABC中,C=90°, (1)若c=10,a:b=3:4,则a=____,b=___.
(2)若a=9,b=40,则c=______.
★在 ABC中, C=90°,若AC=6,CB=8,则ABC面积为_____,斜边为上的高为______.
三、选择题
1、★放学以后,小红和小颖从学校分手,分别沿着东南方向和西南方向回家,若小红和小颖行走的速度都是40米/分,小红用15分钟到家,小颖用20分钟到家,小红和小颖家的距离( )
A、600米; B、800米; C、1000米; D、不能确定
2、★★直角三角形两直角边分别为5厘米、12厘米,那么斜边上的高是 ( )
A、6厘米; B、 8厘米; C、 80/13厘米; D、 60/13厘米;
3、用四个边长均为a、b、c的直角三角板,拼成如图中所示的图形,则下列结论中正确的是( )
A.c2=a2+b2 B.c2=a2+2ab+b2
C.c2=a2-2ab+b2 D.c2=(a+b)2.
4、下列选项中,不能用来证明勾股定理的是( )
A. B. C. D.
5、我国古代数学家赵爽的“勾股方圆图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示),如果大正方形的面积是25,小正方形的面积是1,直角三角形的两直角边分别是a和b,那么(a+b)2的值为( )
A.49 B.25 C.13 D.1
6、利用图(1)或图(2)两个图形中的有关面积的等量关系都能证明数学中一个十分著名的定理,这个定理称为____ __,该定理的结论其数学表达式是 ____ __.
四:归纳总结:
验证勾股定理用的是什么方法?
五、课外作业:
1.★如图,是某沿江地区交通平面图,为了加快经济发展,该地区拟修建一条连接M,O,Q三城市的沿江高速的建设成本是100万元∕千米,该沿江高速的造价是多少?
2.★如图,从电线杆离地面6米处向地面拉一条长10米的缆绳,
这条缆绳在地面的固定点距离电线杆底部有多远?
3.★一直角三角形的斜边比直角边大2,另一直角边长为6,则斜边长为
★直角三角形两直角边分别为5厘米、12厘米,那么斜边上的高是
5.★直角三角形的三边长为连续偶数,则其周长为
6.★以直角三角形的两直角边为边长向外作正方形,所作的正方形的面积分别为9和16,则直角三角形的斜边长为
7.★★如图,是一块直角三角形纸片,两直角边AC=6㎝,BC=8㎝,现将ABC沿直线AD折叠,使AC落在斜边AB上,且与AE重合,求CD的长
8、如图1-4,一架梯子长25米,斜靠在一面墙上,梯子顶端离地面15米,要使梯子顶端离地24米,则梯子的底部在水平方向上应滑动多少米?
9★★★如图7,矩形纸片ABCD的边AB=10,BC=6,E为BC上一点,将矩形纸片沿AE折叠,点B恰好落在CD边上的点G处,求BE的长
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
