人教版数学七年级上册4.2直线、射线、线段 (3) 课件(共14张PPT)
文档属性
| 名称 | 人教版数学七年级上册4.2直线、射线、线段 (3) 课件(共14张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-14 21:36:00 | ||
图片预览




文档简介
(共14张PPT)
4.2 直线、射线、线段
第 3 课时
学习目标
1. 借助现实的情境,了解“两点之间,线段最短”的性质.
2. 理解两点间距离的定义.
3. 会运用“两点之间线段最短”的性质解决生活中的实际问题.
4. 通过探究实际问题得出结论的过程,提高学生的学习兴趣与解决
实际问题的能力.
直线
射线
线段
重点
难点
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
从愚公移山的故事到现代高速公路隧道,体现了人类的智慧与进步.
思考
为什么他们都要这样设计呢
一级标题
应用新知
巩固新知
课堂小结
布置作业
探究新知
创设情境
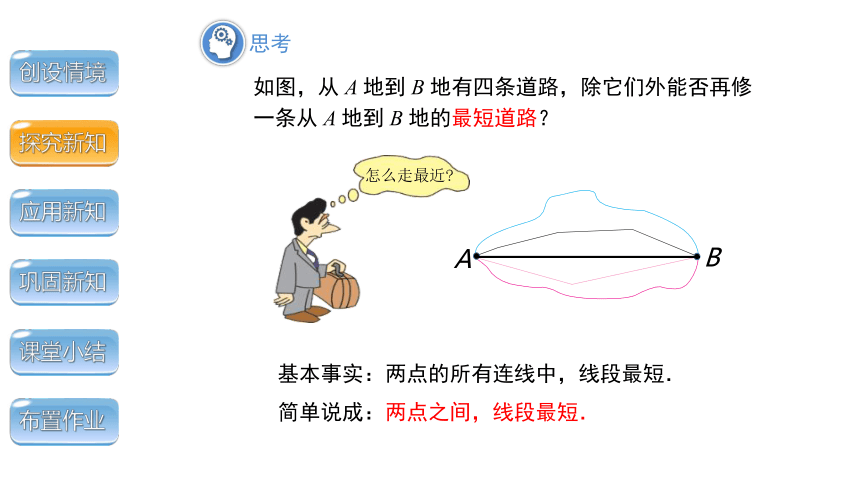
如图,从 A 地到 B 地有四条道路,除它们外能否再修
一条从 A 地到 B 地的最短道路?
思考
怎么走最近
A
B
基本事实:两点的所有连线中,线段最短.
简单说成:两点之间,线段最短.
一级标题
应用新知
巩固新知
课堂小结
布置作业
探究新知
创设情境
思考
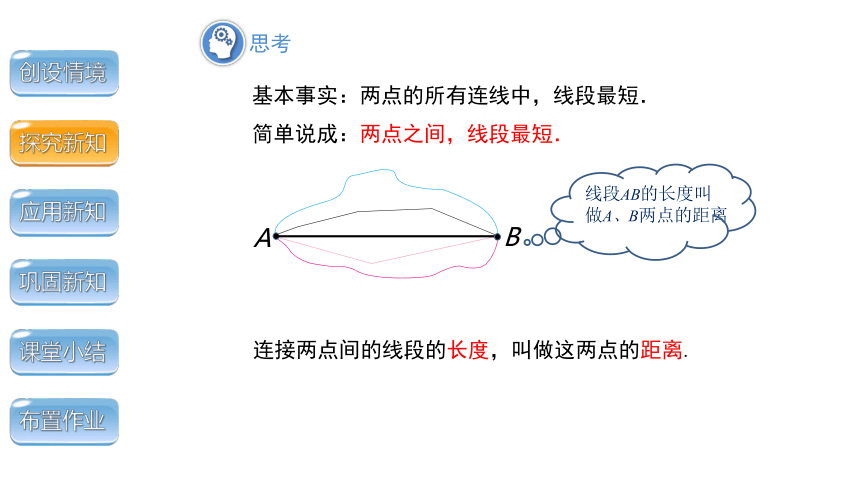
基本事实:两点的所有连线中,线段最短.
简单说成:两点之间,线段最短.
连接两点间的线段的长度,叫做这两点的距离.
线段AB的长度叫做A、B两点的距离
A
B
一级标题
应用新知
巩固新知
课堂小结
布置作业
探究新知
创设情境
绿地里本没有路,为什么大家都喜欢走捷径呢?
两点之间,线段最短.
想一想
一级标题
应用新知
巩固新知
课堂小结
布置作业
探究新知
创设情境
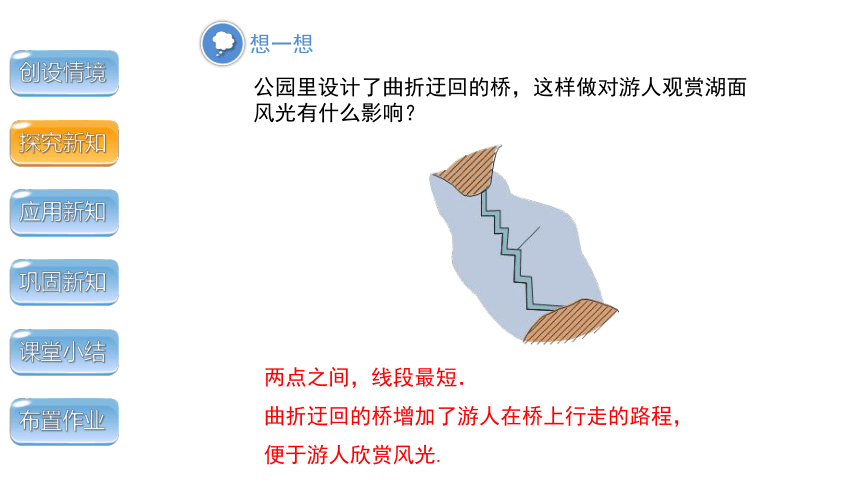
公园里设计了曲折迂回的桥,这样做对游人观赏湖面风光有什么影响?
两点之间,线段最短.
曲折迂回的桥增加了游人在桥上行走的路程,便于游人欣赏风光.
想一想
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
创设情境
例1 如图,把原来弯曲的河道改直,A,B 两地间的河道
长度变短,这样做的道理是( )
A.两点确定一条直线
B.两点确定一条线段
C.两点之间,直线最短
D.两点之间,线段最短
D
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
创设情境
例2 如图:AB+AC_____BC(>,<,=)
理由是:____________________
三角形两边之和大于第三边.
>
两点之间,线段最短.
三角形任意两边之和与第三边的大小关系是什么?
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
随堂练习
1.下列四个生活和生产现象,其中可以用 “两点之间,线段最短”来解释的现象有( )
(1)用两个钉子就可以将木条固定在墙上;
(2)植树时,只要定住两棵树的位置,就能确定同一行树所在
的直线;
(3)从 A 地到 B 地架设电线,总是尽可能沿着线段 AB 架设;
(4)把弯曲的公路改直,就能缩短路程.
(3)
(4)
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
随堂练习
2.一只蚂蚁要从正方体的一个顶点 A 沿表面爬行到顶点 B,怎样爬行路线最短?如果要爬行到顶点 C 呢?
C’
D
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
两点间距离:
基本事实:
两点的所有连线中,线段最短.
简单记为:两点之间,线段最短.
连接两点间的线段的长度,叫做这两点的距离.
直线
射线
线段
布置作业
教科书第130页 习题4.2
第8题
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
4.2 直线、射线、线段
第 3 课时
学习目标
1. 借助现实的情境,了解“两点之间,线段最短”的性质.
2. 理解两点间距离的定义.
3. 会运用“两点之间线段最短”的性质解决生活中的实际问题.
4. 通过探究实际问题得出结论的过程,提高学生的学习兴趣与解决
实际问题的能力.
直线
射线
线段
重点
难点
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
从愚公移山的故事到现代高速公路隧道,体现了人类的智慧与进步.
思考
为什么他们都要这样设计呢
一级标题
应用新知
巩固新知
课堂小结
布置作业
探究新知
创设情境
如图,从 A 地到 B 地有四条道路,除它们外能否再修
一条从 A 地到 B 地的最短道路?
思考
怎么走最近
A
B
基本事实:两点的所有连线中,线段最短.
简单说成:两点之间,线段最短.
一级标题
应用新知
巩固新知
课堂小结
布置作业
探究新知
创设情境
思考
基本事实:两点的所有连线中,线段最短.
简单说成:两点之间,线段最短.
连接两点间的线段的长度,叫做这两点的距离.
线段AB的长度叫做A、B两点的距离
A
B
一级标题
应用新知
巩固新知
课堂小结
布置作业
探究新知
创设情境
绿地里本没有路,为什么大家都喜欢走捷径呢?
两点之间,线段最短.
想一想
一级标题
应用新知
巩固新知
课堂小结
布置作业
探究新知
创设情境
公园里设计了曲折迂回的桥,这样做对游人观赏湖面风光有什么影响?
两点之间,线段最短.
曲折迂回的桥增加了游人在桥上行走的路程,便于游人欣赏风光.
想一想
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
创设情境
例1 如图,把原来弯曲的河道改直,A,B 两地间的河道
长度变短,这样做的道理是( )
A.两点确定一条直线
B.两点确定一条线段
C.两点之间,直线最短
D.两点之间,线段最短
D
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
创设情境
例2 如图:AB+AC_____BC(>,<,=)
理由是:____________________
三角形两边之和大于第三边.
>
两点之间,线段最短.
三角形任意两边之和与第三边的大小关系是什么?
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
随堂练习
1.下列四个生活和生产现象,其中可以用 “两点之间,线段最短”来解释的现象有( )
(1)用两个钉子就可以将木条固定在墙上;
(2)植树时,只要定住两棵树的位置,就能确定同一行树所在
的直线;
(3)从 A 地到 B 地架设电线,总是尽可能沿着线段 AB 架设;
(4)把弯曲的公路改直,就能缩短路程.
(3)
(4)
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
随堂练习
2.一只蚂蚁要从正方体的一个顶点 A 沿表面爬行到顶点 B,怎样爬行路线最短?如果要爬行到顶点 C 呢?
C’
D
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
两点间距离:
基本事实:
两点的所有连线中,线段最短.
简单记为:两点之间,线段最短.
连接两点间的线段的长度,叫做这两点的距离.
直线
射线
线段
布置作业
教科书第130页 习题4.2
第8题
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
