高一数学人教B版选择性必修第二册课件3.1.1基本计数原理 课件(共26张PPT)
文档属性
| 名称 | 高一数学人教B版选择性必修第二册课件3.1.1基本计数原理 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 726.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-13 19:34:07 | ||
图片预览







文档简介
(共26张PPT)
3.1.1 基本计数原理
第三章 排列、组合与二项式定理
问题引入
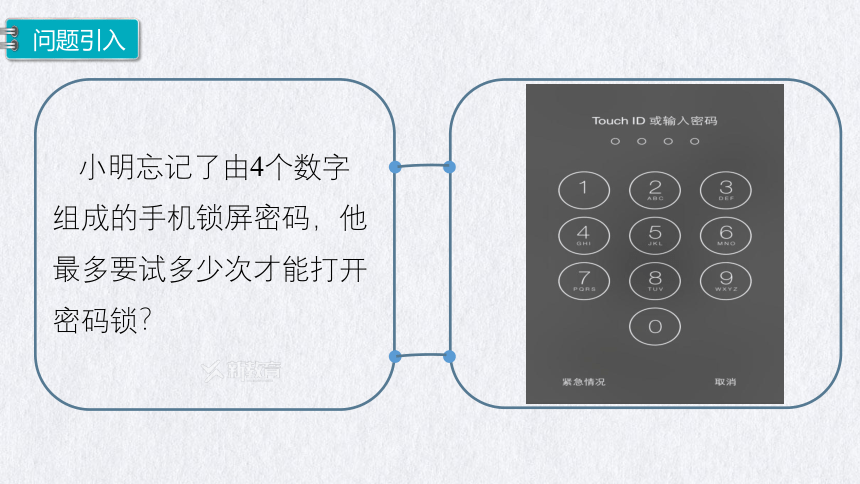
小明忘记了由4个数字组成的手机锁屏密码,他最多要试多少次才能打开密码锁?
新知探索
分类加法计数原理
答案 因为英文字母共有26个,阿拉伯数字共有10个,所以总共可以编出26+10=36(种)不同的号码.
问题1 用一个大写的英文字母或一个阿拉伯数字给教室里的座位编号,总共能编出多少种不同的号码?
新知探索
分类加法计数原理
问题2 问题1中最重要的特征是什么?
答案 最重要的特征是“或”字的出现:每个座位都可以用一个英文字母或一个阿拉伯数字编号,有两类方案.
新知探索
分类加法计数原理
分类加法计数原理
完成一件事有n类不同方案,在第1类方案中有m1种不同的方法,在第2类方案中有m2种不同的方法……在第n类方案中有mn种不同的方法.那么完成这件事共有____________________种不同的方法.
问题3 由问题1你能归纳出一般结论吗?
新知探索
分类加法计数原理
问题4 分类加法计数原理中的“各种方法”与“完成这件事”有什么关系?
答案 分类加法计数原理中的“各种方法”都能独立“完成这件事”,与“其他方法”没关系.
新知探索
分步乘法计数原理
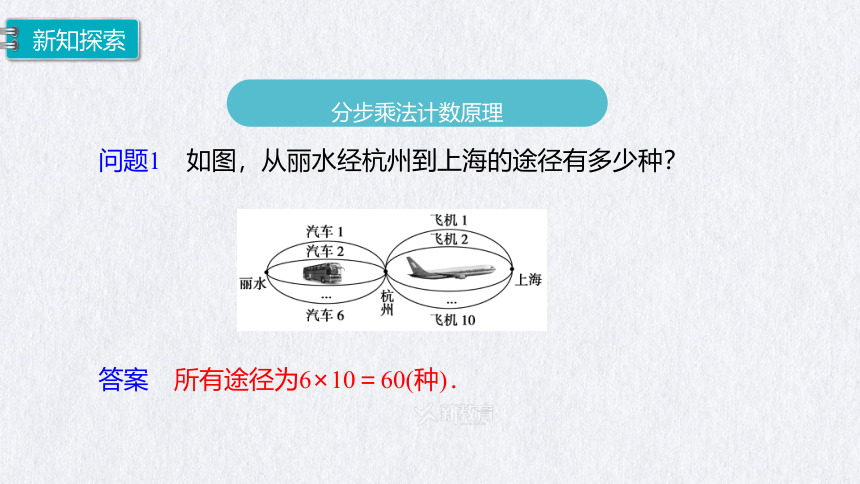
问题1 如图,从丽水经杭州到上海的途径有多少种?
答案 所有途径为6×10=60(种).
新知探索
分步乘法计数原理
问题2 用前6个大写英文字母和1~9九个阿拉伯数字,以A1,A2,…,B1,
B2,…的方式给教室里的座位编号,总共能编出多少个不同的号码?
答案 编写一个号码要先确定一个英文字母,后确定一个
阿拉伯数字,我们可以用树形图列出所有可能的号码.如右图,
由于前6个英文字母中的任意一个都能与9个数字中的任何一个
组成一个号码,而且它们各不相同,因此共有6×9=54(个)不同
的号码.
新知探索
分步乘法计数原理
分步乘法计数原理
完成一件事需要n个步骤,做第1步有m1种不同的方法,做第2步有m2种不同的方法……做第n步有mn种不同的方法,那么完成这件事共有____________________种不同的方法.
问题3 由上述问题1,2,你能归纳猜想出一般结论吗?
新知探索
分步乘法计数原理
问题4 分步乘法计数原理中的“各步方法”与“完成这件事”有什么关系?
答案 要完成这件事,“各步”中的方法必须依次都完成,步与步之间是连续的,且相互依存.
新知探索
两个计数原理的联系与区别
1.联系
分类加法计数原理和分步乘法计数原理都是解决计数问题最基本、最重要的方法.
新知探索
两个计数原理的联系与区别
2.区别
分类加法计数原理 分步乘法计数原理
区别一 完成一件事共有n类办法,关键词是“分类” 完成一件事共有n个步骤,关键词是“分步”
区别二 每类办法中的每种方法都能独立地完成这件事,它是独立的、一次的且每种方法得到的都是最后结果,只需一种方法就可完成这件事 除最后一步外,其他每步得到的只是中间结果,任何一步都不能独立完成这件事,缺少任何一步也不能完成这件事,只有各个步骤都完成了,才能完成这件事
区别三 各类办法之间是互斥的、并列的、独立的 各步之间是关联的、独立的,“关联”确保不遗漏,“独立”确保不重复
典例精析
题型一: 利用分类加法计数原理解题
例1 在所有的两位数中,个位数字比十位数字大的两位数有多少个
解 方法一:分析个位数,可分以下几类:
个位是9,则十位可以是1,2,3,…,8中的一个,故有8个;
个位是8,则十位可以是1,2,3,…,7中的一个,故有7个;
同理,个位是7的有6个;个位是6的有5个;……;个位是2的只有1个.
由分类加法计数原理知,满足条件的两位数有1+2+3+4+5+6+7+8=36(个).
典例精析
题型一: 利用分类加法计数原理解题
例1 在所有的两位数中,个位数字比十位数字大的两位数有多少个
解 方法二:按十位数上的数字分别是1,2,3,4,5,6,7,8的情况分成8类,在每一类中满足题目条件的两位数分别有8个,7个,6个,5个,4个,3个,2个,1个,由分类加法计数原理知,符合题意的两位数共有8+7+6+5+4+3+2+1=36(个).
典例精析
题型一: 利用分类加法计数原理解题
例1 在所有的两位数中,个位数字比十位数字大的两位数有多少个
解 方法三:将个位比十位数字大的两位数一一写出:
12,13,14,15,16,17,18,19,
23,24,25,26,27,28,29,
34,35,36,37,38,39,
45,46,47,48,49,
56,57,58,59,
67,68,69,
78,79,
89. 共有36个符合题意的两位数.
反思感悟
利用分类加法计数原理解题的一般思路
(1)分类:将完成这件事的办法分成若干类;
(2)计数:求出每一类中的方法数;
(3)结论:将每一类中的方法数相加得最终结果.
典例精析
题型二:利用分步乘法计数原理解题
例2 已知a∈{1,2,3},b∈{4,5,6,7},r∈{8,9},则方程(x-a)2+(y-b)2=r2可表示多少个不同的圆
解 完成表示不同的圆这件事,可以分为三步:
第一步:确定a有3种不同的选取方法;
第二步:确定b有4种不同的选取方法;
第三步:确定r有2种不同的选取方法;
由分步乘法计数原理知,方程(x-a)2+(y-b)2=r2可表示不同的圆共有3×4×2=24(个).
反思感悟
利用分步乘法计数原理解题的一般思路
(1)分步:将完成这件事的过程分成若干步;
(2)计数:求出每一步中的方法数;
(3)结论:将每一步中的方法数相乘得最终结果.
典例精析
题型三:两个原理的综合应用
例3 编号为A,B,C,D,E的五个小球,放到如图所示的五个盒子中,要求每个盒子只能放一个小球,且A球不能放到1,2号,B球必须放到与A相邻的盒子中,有多少种不同的放法
解 根据A球的位置分三类.
(1)若A球放入3号盒里,则B球只能放在4号盒里,剩下的三个盒子分别放C,D,E三球,共有3×2×1=6种放法.
(2)若A球放入5号盒子里,则B球只能放入4号盒中,剩下的三个盒子分别放C,D,E三球,共有3×2×1=6种放法.
(3)若A球放入4号盒子里,则B球可以放到2号、3号或5号盒子中,剩下的三个盒子分别放C,D,E三球,有3×3×2×1=18种放法.
综合上述,由分类加法计数原理得不同放法共有6+6+18=30种.
反思感悟
应用两个计数原理解题的策略:
对于两个计数原理的综合应用问题,一般是先分类再分步,分类时要设计好标准,设计好分类方案,防止重复和遗漏;分步时要注意步与步之间的连续性,同时应合理设计步骤的顺序,使各步互不干扰,也可以根据题意恰当合理地画出示意图或者列出表格,使问题的实质直观地显现出来,从而便于我们解题.
跟踪练习
√
解析 要完成配套,分两步:第1步,选上衣,从4件上衣中任选一件,有4种不同选法;第2步,选长裤,从3条长裤中任选一条,有3种不同选法.故共有4×3=12(种)不同的配法.
跟踪练习
2.由0,1,2三个数字组成的三位数(允许数字重复)的个数为( )
A.27 B.18 C.12 D.6
解析 分三步,依次取个位、十位、百位上的数字,分别有3种、3种、2种取法,故共可得3×3×2=18个不同的三位数.
√
跟踪练习
√
3.三人踢毽子,互相传递,每人每次只能踢一下.由甲开始踢,经过4次传递后,毽子又被踢回甲,则不同的传递方式共有( )
A.4种 B.5种 C.6种 D.12种
解析 若甲先传给乙,则有甲→乙→甲→乙→甲,甲→乙→甲→丙→甲,甲→乙→丙→乙→甲3种不同的传递方式;同理,甲先传给丙也有3种不同的传递方式.故共有6种不同的传递方式.
跟踪练习
4.如图所示的电路图,从A到B共有 条不同的线路可通电.
解析 先分三类.第一类,经过支路①有3种方法;
第二类,经过支路②有1种方法;
第三类,经过支路③有2×2=4种方法,
所以总的线路条数N=3+1+4=8.
8
课堂小结
谢
指
导
谢
3.1.1 基本计数原理
第三章 排列、组合与二项式定理
问题引入
小明忘记了由4个数字组成的手机锁屏密码,他最多要试多少次才能打开密码锁?
新知探索
分类加法计数原理
答案 因为英文字母共有26个,阿拉伯数字共有10个,所以总共可以编出26+10=36(种)不同的号码.
问题1 用一个大写的英文字母或一个阿拉伯数字给教室里的座位编号,总共能编出多少种不同的号码?
新知探索
分类加法计数原理
问题2 问题1中最重要的特征是什么?
答案 最重要的特征是“或”字的出现:每个座位都可以用一个英文字母或一个阿拉伯数字编号,有两类方案.
新知探索
分类加法计数原理
分类加法计数原理
完成一件事有n类不同方案,在第1类方案中有m1种不同的方法,在第2类方案中有m2种不同的方法……在第n类方案中有mn种不同的方法.那么完成这件事共有____________________种不同的方法.
问题3 由问题1你能归纳出一般结论吗?
新知探索
分类加法计数原理
问题4 分类加法计数原理中的“各种方法”与“完成这件事”有什么关系?
答案 分类加法计数原理中的“各种方法”都能独立“完成这件事”,与“其他方法”没关系.
新知探索
分步乘法计数原理
问题1 如图,从丽水经杭州到上海的途径有多少种?
答案 所有途径为6×10=60(种).
新知探索
分步乘法计数原理
问题2 用前6个大写英文字母和1~9九个阿拉伯数字,以A1,A2,…,B1,
B2,…的方式给教室里的座位编号,总共能编出多少个不同的号码?
答案 编写一个号码要先确定一个英文字母,后确定一个
阿拉伯数字,我们可以用树形图列出所有可能的号码.如右图,
由于前6个英文字母中的任意一个都能与9个数字中的任何一个
组成一个号码,而且它们各不相同,因此共有6×9=54(个)不同
的号码.
新知探索
分步乘法计数原理
分步乘法计数原理
完成一件事需要n个步骤,做第1步有m1种不同的方法,做第2步有m2种不同的方法……做第n步有mn种不同的方法,那么完成这件事共有____________________种不同的方法.
问题3 由上述问题1,2,你能归纳猜想出一般结论吗?
新知探索
分步乘法计数原理
问题4 分步乘法计数原理中的“各步方法”与“完成这件事”有什么关系?
答案 要完成这件事,“各步”中的方法必须依次都完成,步与步之间是连续的,且相互依存.
新知探索
两个计数原理的联系与区别
1.联系
分类加法计数原理和分步乘法计数原理都是解决计数问题最基本、最重要的方法.
新知探索
两个计数原理的联系与区别
2.区别
分类加法计数原理 分步乘法计数原理
区别一 完成一件事共有n类办法,关键词是“分类” 完成一件事共有n个步骤,关键词是“分步”
区别二 每类办法中的每种方法都能独立地完成这件事,它是独立的、一次的且每种方法得到的都是最后结果,只需一种方法就可完成这件事 除最后一步外,其他每步得到的只是中间结果,任何一步都不能独立完成这件事,缺少任何一步也不能完成这件事,只有各个步骤都完成了,才能完成这件事
区别三 各类办法之间是互斥的、并列的、独立的 各步之间是关联的、独立的,“关联”确保不遗漏,“独立”确保不重复
典例精析
题型一: 利用分类加法计数原理解题
例1 在所有的两位数中,个位数字比十位数字大的两位数有多少个
解 方法一:分析个位数,可分以下几类:
个位是9,则十位可以是1,2,3,…,8中的一个,故有8个;
个位是8,则十位可以是1,2,3,…,7中的一个,故有7个;
同理,个位是7的有6个;个位是6的有5个;……;个位是2的只有1个.
由分类加法计数原理知,满足条件的两位数有1+2+3+4+5+6+7+8=36(个).
典例精析
题型一: 利用分类加法计数原理解题
例1 在所有的两位数中,个位数字比十位数字大的两位数有多少个
解 方法二:按十位数上的数字分别是1,2,3,4,5,6,7,8的情况分成8类,在每一类中满足题目条件的两位数分别有8个,7个,6个,5个,4个,3个,2个,1个,由分类加法计数原理知,符合题意的两位数共有8+7+6+5+4+3+2+1=36(个).
典例精析
题型一: 利用分类加法计数原理解题
例1 在所有的两位数中,个位数字比十位数字大的两位数有多少个
解 方法三:将个位比十位数字大的两位数一一写出:
12,13,14,15,16,17,18,19,
23,24,25,26,27,28,29,
34,35,36,37,38,39,
45,46,47,48,49,
56,57,58,59,
67,68,69,
78,79,
89. 共有36个符合题意的两位数.
反思感悟
利用分类加法计数原理解题的一般思路
(1)分类:将完成这件事的办法分成若干类;
(2)计数:求出每一类中的方法数;
(3)结论:将每一类中的方法数相加得最终结果.
典例精析
题型二:利用分步乘法计数原理解题
例2 已知a∈{1,2,3},b∈{4,5,6,7},r∈{8,9},则方程(x-a)2+(y-b)2=r2可表示多少个不同的圆
解 完成表示不同的圆这件事,可以分为三步:
第一步:确定a有3种不同的选取方法;
第二步:确定b有4种不同的选取方法;
第三步:确定r有2种不同的选取方法;
由分步乘法计数原理知,方程(x-a)2+(y-b)2=r2可表示不同的圆共有3×4×2=24(个).
反思感悟
利用分步乘法计数原理解题的一般思路
(1)分步:将完成这件事的过程分成若干步;
(2)计数:求出每一步中的方法数;
(3)结论:将每一步中的方法数相乘得最终结果.
典例精析
题型三:两个原理的综合应用
例3 编号为A,B,C,D,E的五个小球,放到如图所示的五个盒子中,要求每个盒子只能放一个小球,且A球不能放到1,2号,B球必须放到与A相邻的盒子中,有多少种不同的放法
解 根据A球的位置分三类.
(1)若A球放入3号盒里,则B球只能放在4号盒里,剩下的三个盒子分别放C,D,E三球,共有3×2×1=6种放法.
(2)若A球放入5号盒子里,则B球只能放入4号盒中,剩下的三个盒子分别放C,D,E三球,共有3×2×1=6种放法.
(3)若A球放入4号盒子里,则B球可以放到2号、3号或5号盒子中,剩下的三个盒子分别放C,D,E三球,有3×3×2×1=18种放法.
综合上述,由分类加法计数原理得不同放法共有6+6+18=30种.
反思感悟
应用两个计数原理解题的策略:
对于两个计数原理的综合应用问题,一般是先分类再分步,分类时要设计好标准,设计好分类方案,防止重复和遗漏;分步时要注意步与步之间的连续性,同时应合理设计步骤的顺序,使各步互不干扰,也可以根据题意恰当合理地画出示意图或者列出表格,使问题的实质直观地显现出来,从而便于我们解题.
跟踪练习
√
解析 要完成配套,分两步:第1步,选上衣,从4件上衣中任选一件,有4种不同选法;第2步,选长裤,从3条长裤中任选一条,有3种不同选法.故共有4×3=12(种)不同的配法.
跟踪练习
2.由0,1,2三个数字组成的三位数(允许数字重复)的个数为( )
A.27 B.18 C.12 D.6
解析 分三步,依次取个位、十位、百位上的数字,分别有3种、3种、2种取法,故共可得3×3×2=18个不同的三位数.
√
跟踪练习
√
3.三人踢毽子,互相传递,每人每次只能踢一下.由甲开始踢,经过4次传递后,毽子又被踢回甲,则不同的传递方式共有( )
A.4种 B.5种 C.6种 D.12种
解析 若甲先传给乙,则有甲→乙→甲→乙→甲,甲→乙→甲→丙→甲,甲→乙→丙→乙→甲3种不同的传递方式;同理,甲先传给丙也有3种不同的传递方式.故共有6种不同的传递方式.
跟踪练习
4.如图所示的电路图,从A到B共有 条不同的线路可通电.
解析 先分三类.第一类,经过支路①有3种方法;
第二类,经过支路②有1种方法;
第三类,经过支路③有2×2=4种方法,
所以总的线路条数N=3+1+4=8.
8
课堂小结
谢
指
导
谢
