9.1向量概念 课件(共23张PPT)
文档属性
| 名称 | 9.1向量概念 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-13 00:00:00 | ||
图片预览







文档简介
(共23张PPT)
第9章 平面向量
§9.1 向量概念
学习目标
1.理解向量的物理背景,从位移、速度、力等物理量抽象概括出向量的概念;
2.掌握利用有向线段表示向量,理解向量的模的概念;
3.掌握零向量,单位向量的概念;
4.理解相等向量、共线向量;
5.掌握向量的夹角.
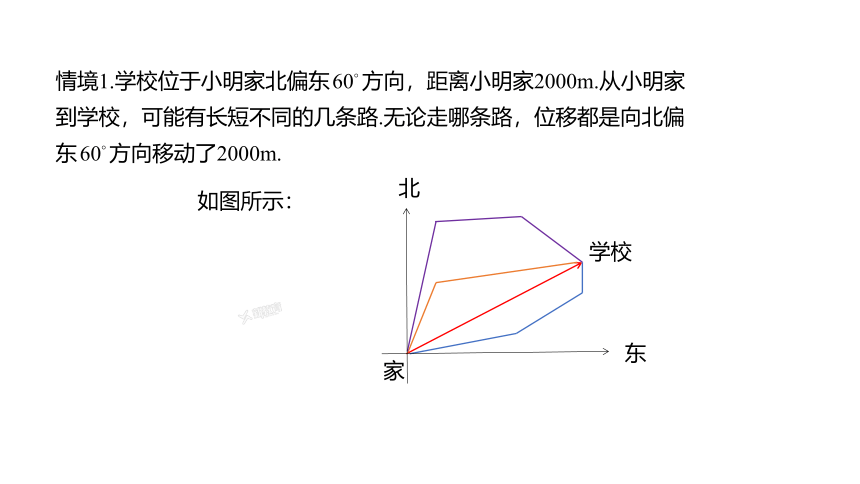
情境1.学校位于小明家北偏东 方向,距离小明家2000m.从小明家到学校,可能有长短不同的几条路.无论走哪条路,位移都是向北偏东 方向移动了2000m.
如图所示:
家
学校
东
北
情境2.某著名运动员投掷标枪时,其中一次记录为:
出手角度 ,出手速度为v=28.35m/s.
如图所示:
情境3.汽车沿倾斜角为 的坡路向上行驶,汽车的牵引力为F.
如图所示:
思考1.上面三个情境中反映的的物理量有什么共同特点?
2.请再举出一些含有类似性质的物理量实例进行分析.
数学中,把既有大小,又有方向的量叫做向量,
把只有大小,没有方向的量称为数量.
那么年龄、身高、体重、面积、体积、温度、路程等是向量吗?
对于一个实数,可以用数轴上的点表示;
对于一个二次函数,可以用一条抛物线表示…….
数学中有许多量都可以用几何方式表示,
你认为如何用几何方式表示向量最合适?
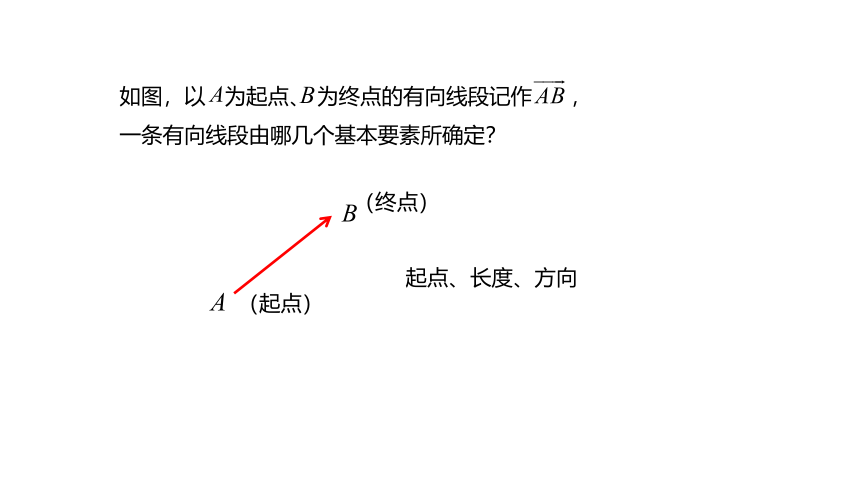
如图,以 为起点、 为终点的有向线段记作 ,
一条有向线段由哪几个基本要素所确定?
起点、长度、方向
(起点)
(终点)
有向线段 的长度就是指线段 的长度,
也称为向量 的长度或模,
它表示向量 的大小,记作 .
如果表示向量的有向线段没有标注起点和终点字母,
向量也可以用黑体字母 表示,
如图,此时向量的模怎样表示?
模为0的向量叫做零向量,记作 ;
怎样理解零向量的方向?
大小为0,方向不确定的.可以是任意方向.
模为1个单位的向量叫做单位向量.
例1.小明从学校的的教学楼出发,向北走了1500m到达图书馆,
2h后又从图书馆向南偏东 走了1000m到食堂就餐,用餐后
又从食堂向西走了2000m来到操场运动,请选择适当的比例尺
画图,用向量表示小明每次的位移.
A (图书馆)
O (教学楼)
C (操场)
B (食堂)
解:设比例尺为1:50000,如图所示,
小明的位移表示如下:
向量 表示从教学楼到图书馆的距离和方向;
向量 表示从图书馆到食堂的距离和方向;
向量 表示从食堂到操场的距离和方向.
相等向量:
长度相等且方向相同的向量.
记作: .
共线向量:方向 或 的非零向量,也叫做平行向量.
相同
相反
规定:零向量与任一向量平行.
记作: // .
如下图: , 平行:
相反向量:
长度相等且方向相反的向量.
向量 的相反向量记作 .
例2.判断下列命题真假或给出问题的答案:
(1)平行向量的方向一定相同.
(2)不相等的向量一定不平行.
(4)存在与任何向量都平行的向量吗?
(5)若两个向量在同一直线上,则这两个向量一定是什么向量?
(6)两个非零向量相等的条件是什么?
(3)共线向量一定在同一直线上.
×
×
零向量
平行向量(共线向量)
模相等且方向相同
×
例3.如图,设 是正六边形的中心,分别写出图中与向量 、 、 相等的向量.
向量的夹角
O
A
B
两个非零向量 和 ,作 , ,则
叫做向量 和 的夹角.
O
A
B
若 , 与 同向.
O
A
B
若 , 与 反向.
O
A
B
O
B
若 , 与 垂直,
记作
O
A
B
例4.如图,设 是正六边形的中心,分别写出下列向量的夹角.
(1) 与 ;
(2) 与 ;
(3) 与 ;
(4) 与 .
课堂小结
1.向量的概念——既有大小又有方向的量.
2.向量的表示——有向线段.
3.零向量、单位向量、相等向量、共线向量.
4.向量的夹角.
第9章 平面向量
§9.1 向量概念
学习目标
1.理解向量的物理背景,从位移、速度、力等物理量抽象概括出向量的概念;
2.掌握利用有向线段表示向量,理解向量的模的概念;
3.掌握零向量,单位向量的概念;
4.理解相等向量、共线向量;
5.掌握向量的夹角.
情境1.学校位于小明家北偏东 方向,距离小明家2000m.从小明家到学校,可能有长短不同的几条路.无论走哪条路,位移都是向北偏东 方向移动了2000m.
如图所示:
家
学校
东
北
情境2.某著名运动员投掷标枪时,其中一次记录为:
出手角度 ,出手速度为v=28.35m/s.
如图所示:
情境3.汽车沿倾斜角为 的坡路向上行驶,汽车的牵引力为F.
如图所示:
思考1.上面三个情境中反映的的物理量有什么共同特点?
2.请再举出一些含有类似性质的物理量实例进行分析.
数学中,把既有大小,又有方向的量叫做向量,
把只有大小,没有方向的量称为数量.
那么年龄、身高、体重、面积、体积、温度、路程等是向量吗?
对于一个实数,可以用数轴上的点表示;
对于一个二次函数,可以用一条抛物线表示…….
数学中有许多量都可以用几何方式表示,
你认为如何用几何方式表示向量最合适?
如图,以 为起点、 为终点的有向线段记作 ,
一条有向线段由哪几个基本要素所确定?
起点、长度、方向
(起点)
(终点)
有向线段 的长度就是指线段 的长度,
也称为向量 的长度或模,
它表示向量 的大小,记作 .
如果表示向量的有向线段没有标注起点和终点字母,
向量也可以用黑体字母 表示,
如图,此时向量的模怎样表示?
模为0的向量叫做零向量,记作 ;
怎样理解零向量的方向?
大小为0,方向不确定的.可以是任意方向.
模为1个单位的向量叫做单位向量.
例1.小明从学校的的教学楼出发,向北走了1500m到达图书馆,
2h后又从图书馆向南偏东 走了1000m到食堂就餐,用餐后
又从食堂向西走了2000m来到操场运动,请选择适当的比例尺
画图,用向量表示小明每次的位移.
A (图书馆)
O (教学楼)
C (操场)
B (食堂)
解:设比例尺为1:50000,如图所示,
小明的位移表示如下:
向量 表示从教学楼到图书馆的距离和方向;
向量 表示从图书馆到食堂的距离和方向;
向量 表示从食堂到操场的距离和方向.
相等向量:
长度相等且方向相同的向量.
记作: .
共线向量:方向 或 的非零向量,也叫做平行向量.
相同
相反
规定:零向量与任一向量平行.
记作: // .
如下图: , 平行:
相反向量:
长度相等且方向相反的向量.
向量 的相反向量记作 .
例2.判断下列命题真假或给出问题的答案:
(1)平行向量的方向一定相同.
(2)不相等的向量一定不平行.
(4)存在与任何向量都平行的向量吗?
(5)若两个向量在同一直线上,则这两个向量一定是什么向量?
(6)两个非零向量相等的条件是什么?
(3)共线向量一定在同一直线上.
×
×
零向量
平行向量(共线向量)
模相等且方向相同
×
例3.如图,设 是正六边形的中心,分别写出图中与向量 、 、 相等的向量.
向量的夹角
O
A
B
两个非零向量 和 ,作 , ,则
叫做向量 和 的夹角.
O
A
B
若 , 与 同向.
O
A
B
若 , 与 反向.
O
A
B
O
B
若 , 与 垂直,
记作
O
A
B
例4.如图,设 是正六边形的中心,分别写出下列向量的夹角.
(1) 与 ;
(2) 与 ;
(3) 与 ;
(4) 与 .
课堂小结
1.向量的概念——既有大小又有方向的量.
2.向量的表示——有向线段.
3.零向量、单位向量、相等向量、共线向量.
4.向量的夹角.
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
