1.1.3交集与并集

(共13张PPT)
数学之美：美丽的几何图形
复习：
表示：CsA=｛x|x∈S,但x A｝
{x|0｛0,2,4｝
练习：1、如果全集U={x|0≤X<6,X∈Z},A=｛1,3,5｝,
B=｛1,4｝那么，CUA=
CUB=
2、如果全集U={x|0则CUA=
｛0,2,3,5｝。
补集：一般地，设S是一个集合，A是S的一个子集（即A S），由S中所有不属于A的元素组成的集合，叫做S中子集A的补集（或余集）。
A
B
A
B
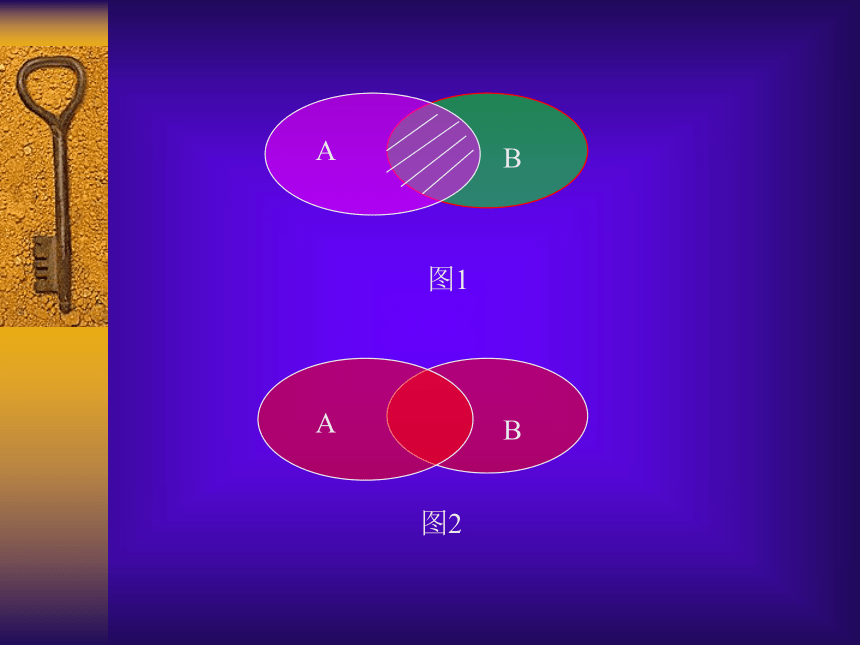
图2
图1
1、交集：一般地，由所有属于集合A且属于集合B的元素所组成的集合,叫做A与B的交集．
记作A∩B（读作＂A交B＂）
即 ：A∩B=｛x|x∈A，且x∈B｝
A
B
图1
例如：Ａ＝｛a,b,c,d,e｝,B={c,d,e,f}.则A∩B={c,d,e}
2、并集：一般地，由所有属于集合A或属于集合B的元素所组成的集合，叫做A与B的并集．
记作：A∪B（读作＂A并B＂）
即：A∪B={x|x∈A，或x∈B})
A
B
图2
例如：A=｛1,2,3,6｝，B=｛1,2,5,10｝， 则 A ∪ B=｛1,2,3,5,6,10｝．
例1．设A=｛x|x>-2｝,B=｛x|x<3｝，求:A∩B ，A ∪ B。
2．设A=｛x|x是等腰三角形｝，B=｛x|x是直角三角形｝，求:A∩B 。
3．A=｛4,5,6,8｝,B=｛3,5,7,8｝，求: A∩B ，A ∪ B。
解： A∩B=｛x|x>-2｝∩｛x|x<3｝=｛x|-2A ∪ B =｛x|x>-2｝ ∪ ｛x|x<3｝=R
解：A∩B=｛x|x是等腰三角形｝∩｛x|x是直角三角形｝=｛x|x是等腰直角三角形｝
解： A∩B ={4，5，6，8} ∩ {3，5，7，8}
={5，8}
A∪B=｛3,4,5,6,7,8｝
练习一：教材12页练习题。
解：A ∩ B=｛x| -31.5 ｝= ｛x|-3A∪B=｛x| -31.5 }=R．
练习二：1、设A=｛x|-31.5｝，求： A∩B ，A∪B.
2、设A=｛x|０　　求；A∩B， A∪B.
解：Ａ＝｛x|0A ∩ B=｛x|-1=｛x|１　　A∪B=｛x|-1练习三：１、已知A={x|-１a},若A∩B=Ф,则实数a的取值范围为：
2、已知A={x|x≤4}, B={x|x>a},若A ∪ B=R,则实数a的取值范围为：
a ≤ 4
a 7
{x| -5 x 2}
1.已知全集U={a,b,c,d,e}，集合A={b,c}，B={c,d},则 (CU A )∩ B等于 （ ）
A.{a,e} B.{b,c,d} C.{a,c,e} D.{d}
2.集合A={x||x+1|=1}，B={x||x|=1}则A∪B等于（ ）
A.{-1,1} B.{-2,-1,1} C.{-1 , 0 , 1} D.{-2 , -1 , 0 , 1}
3.设全集U={x|-5 x 5},A={x|24.已知:全集U=R,M= {x|x 1+ ,x∈ R},N={1,2,3,4}
则： （CU M） ∩N=
{3，4}
D
D
小测试：
小结：
１、交集和并集的概念及表示法；
２、利用求两个集合的交集和集 ；
作业：
3、注意运用数形结合的思想法。