24.2.2直线与圆的位置关系(1)(浙江省台州市路桥区)
文档属性
| 名称 | 24.2.2直线与圆的位置关系(1)(浙江省台州市路桥区) |

|
|
| 格式 | rar | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-09-27 00:00:00 | ||
图片预览



文档简介
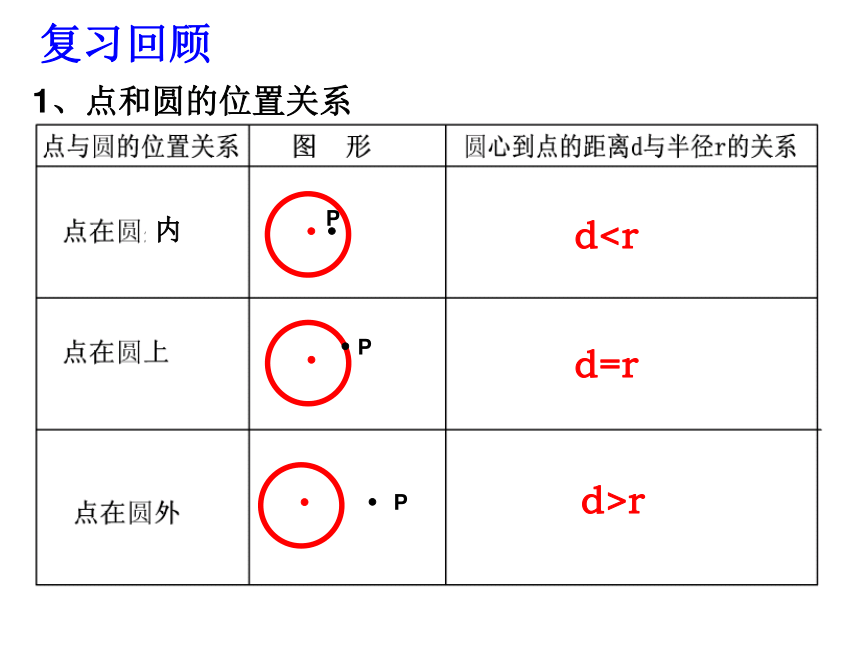
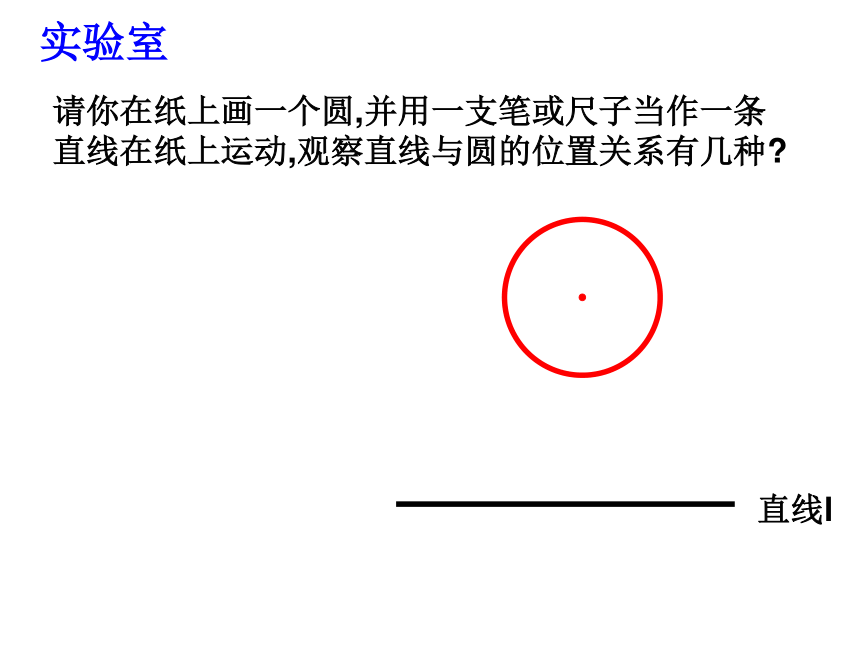
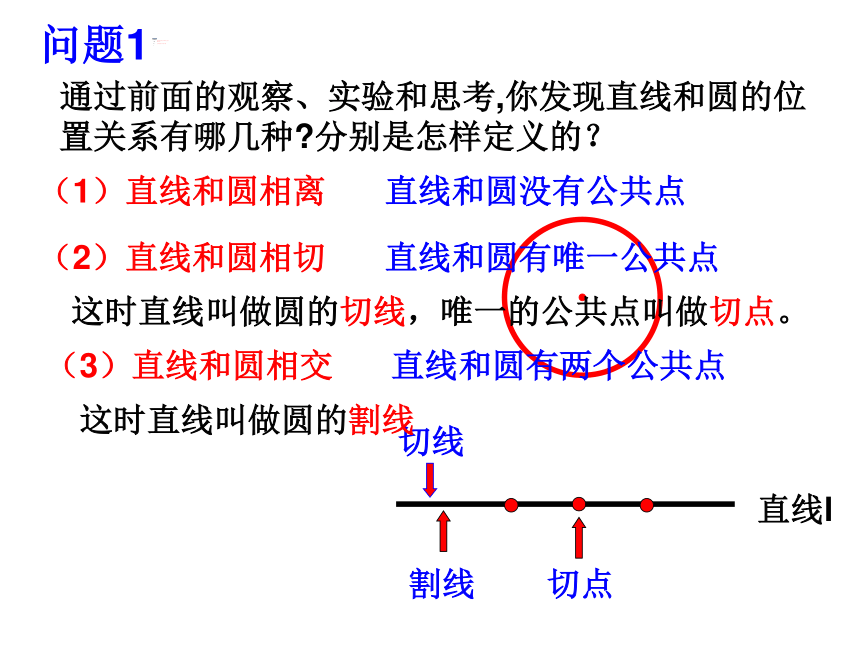
课件16张PPT。地平线内dr1、点和圆的位置关系复习回顾是唐朝诗人王维的诗句,它描述了黄昏日落时分塞外特有的景象。如果我们把太阳看成一个圆,地平线看成一条直线,结合点与圆的位置关系,你觉得,这几幅图片描述了一种什么样的位置关系呢?“大漠孤烟直,长河落日圆”24.2.2 直线与圆的位置关系(1)生活中还有哪些例子,都给我们直线与圆的位置关系的印象.你能举出1—2个实例吗? 请你在纸上画一个圆,并用一支笔或尺子当作一条直线在纸上运动,观察直线与圆的位置关系有几种?实验室直线l通过前面的观察、实验和思考,你发现直线和圆的位置关系有哪几种?分别是怎样定义的?直线和圆没有公共点(1)直线和圆相离直线l直线和圆有唯一公共点(2)直线和圆相切这时直线叫做圆的切线,唯一的公共点叫做切点。切线切点直线和圆有两个公共点(3)直线和圆相交这时直线叫做圆的割线割线问题1“直线和圆的位置关系”能否像“点和圆的位置关系”一样进行数量分析?问题2设圆O的半径为r,圆心O到直线l 的距离为d,问题2设圆O的半径为r,
圆心O到直线l 的距离为d,(1)直线l与圆O相交(2)直线l与圆O相切(3)直线l与圆O相离 2交点dr归纳总结例题分析例1:在RtΔ ABC中,∠C=90o,AC=4cm,BC=3cm,以C为圆心,r为半径的圆与AB有怎样的位置关系?为什么?(1)r=2cm; (2)r=2.4cm; (3)r=3cm分析:ABCd要判定圆C与AB的位置关系,只要先求出圆心C到直线AB的距离d,再与圆C的半径r进行比较即可,因此作斜边AB上的高线.D例题分析例1:在RtΔ ABC中,∠C=90o,AC=4cm,BC=3cm,以C为圆心,r为半径的圆与AB有怎样的位置关系?为什么?(1)r=2cm; (2)r=2.4cm; (3)r=3cmABCdD解:作CD┴AB于点D因为∠ACB=90o,AC=4,BC=3所以AB=5因为所以CD=2.4,即d=2.4cm(1)当r=2时,d>r,则圆C与AB相离.(2)当r=2.4时,d=r,则圆C与AB相切.(3)当r=3时,dr2、本节课从运动变化的观点研究了直线与圆的位置关系,通过点与圆的位置关系类比,运用分类、数形结合思想,得到了直线与圆的位置关系。课堂小结 希望大家如这朝阳,
越升越高!越开越艳!作业:作业本再 见 !
圆心O到直线l 的距离为d,(1)直线l与圆O相交(2)直线l与圆O相切(3)直线l与圆O相离 2交点d
越升越高!越开越艳!作业:作业本再 见 !
同课章节目录
