15.3等腰三角形-—等腰三角形的计算或证明 课件(共40张PPT) 2023--2024学年沪科版数学八年级上册
文档属性
| 名称 | 15.3等腰三角形-—等腰三角形的计算或证明 课件(共40张PPT) 2023--2024学年沪科版数学八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 754.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-14 22:08:42 | ||
图片预览




文档简介
(共40张PPT)
沪科版八年级上册数学
等腰三角形的计算或证明
等腰三角形中角度或线段的相关计算
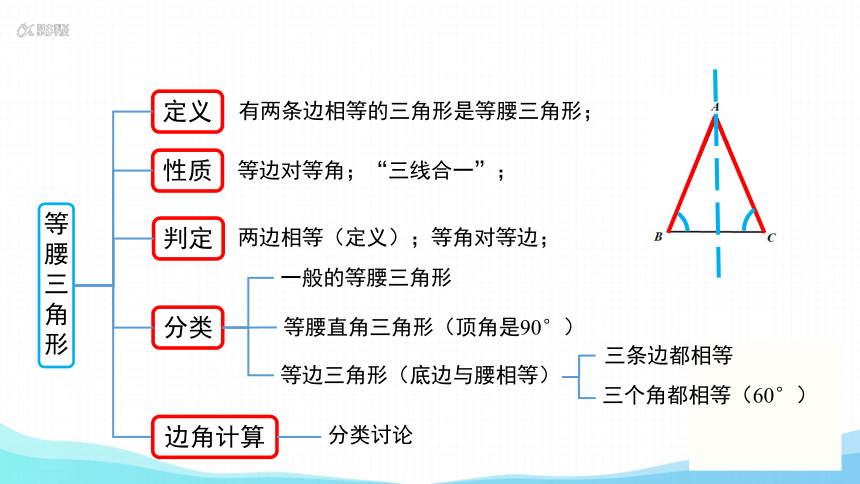
等腰三角形
定义
性质
判定
分类
有两条边相等的三角形是等腰三角形;
等边对等角;“三线合一”;
两边相等(定义);等角对等边;
一般的等腰三角形
等腰直角三角形(顶角是90°)
等边三角形(底边与腰相等)
边角计算
分类讨论
三条边都相等
三个角都相等(60°)
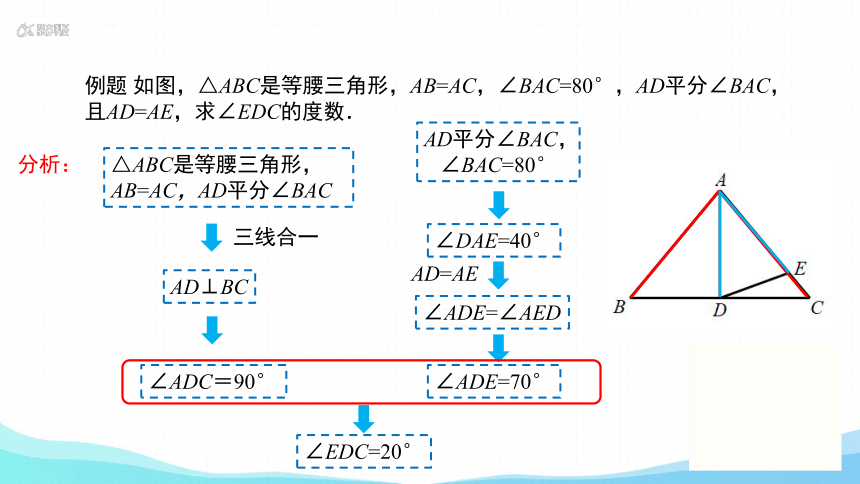
例题 如图,△ABC是等腰三角形,AB=AC,∠BAC=80°,AD平分∠BAC,
且AD=AE,求∠EDC的度数.
分析:
△ABC是等腰三角形,
AB=AC,AD平分∠BAC
三线合一
AD⊥BC
∠ADC=90°
∠ADE=70°
AD平分∠BAC,
∠BAC=80°
AD=AE
∠ADE=∠AED
∠DAE=40°
∠EDC=20°
解:
∵ △ABC是等腰三角形,
AB=AC ,
AD平分∠BAC ,
∴ AD⊥BC.
∴∠ADC=90°.
在△ADE中,
∵ AD=AE,
∴∠ADE=∠AED.
∴∠EDC=∠ADC -∠ADE=20°.
∵∠BAC=80°,
∴∠DAE=40°.
∵∠ADE+∠AED+∠DAE=180°.
∴2∠ADE+40°=180 °.
∴∠ADE=70°.
小结:由等腰三角形顶角的平分线可以推出底边上的高进而得到直角,同时可以找到顶角的一半的度数;依据等边对等角,可以找到等腰三角形中相等的角,知一求二得到三角形每个角的度数.对于求角度的题目,在解题中需要寻求跟求角度相关的条件.
例题 如图,△ABC是等腰三角形,AB=AC,∠BAC=80°,AD平分∠BAC,
且AD=AE,求∠EDC的度数.
70°
20°
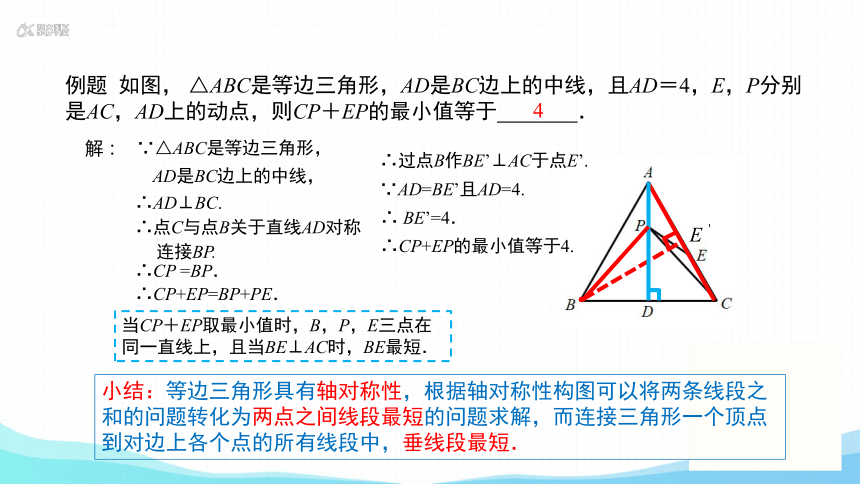
例题 如图, △ABC是等边三角形,AD是BC边上的中线,且AD=4,E,P分别是AC,AD上的动点,则CP+EP的最小值等于 .
等边三角形具有轴对称性
CP=BP
CP+EP
BP+EP
BP+EP的最小值
BE的长
两点之间,
线段最短
分析:
BE的最小值
点到直线的距离
——垂线段的长度
过点B作AC的垂线段
例题 如图, △ABC是等边三角形,AD是BC边上的中线,且AD=4,E,P分别是AC,AD上的动点,则CP+EP的最小值等于 .
AD是BC边上的中线,
∴AD⊥BC.
∴CP+EP的最小值等于4.
小结:等边三角形具有轴对称性,根据轴对称性构图可以将两条线段之和的问题转化为两点之间线段最短的问题求解,而连接三角形一个顶点到对边上各个点的所有线段中,垂线段最短.
解:
∵△ABC是等边三角形,
∴过点B作BE’⊥AC于点E’.
∵AD=BE’且AD=4.
∴ BE’=4.
∴点C与点B关于直线AD对称
∴CP =BP.
∴CP+EP=BP+PE.
当CP+EP取最小值时,B,P,E三点在同一直线上,且当BE⊥AC时,BE最短.
4
连接BP.
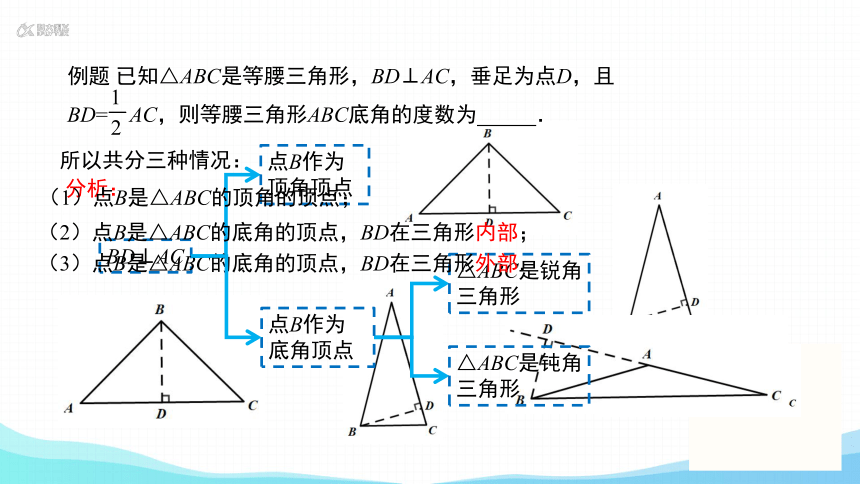
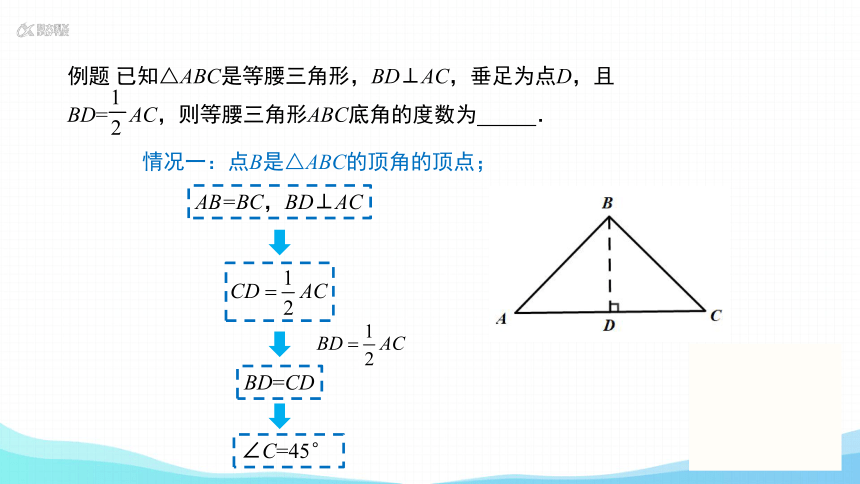
例题 已知△ABC是等腰三角形,BD⊥AC,垂足为点D,且
BD= AC,则等腰三角形ABC底角的度数为 .
BD⊥AC
点B作为
顶角顶点
△ABC是锐角三角形
分析:
所以共分三种情况:
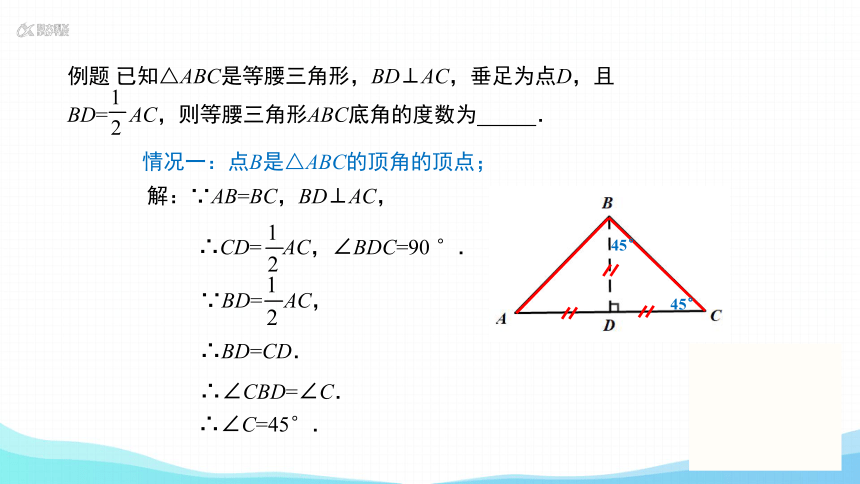
(1)点B是△ABC的顶角的顶点;
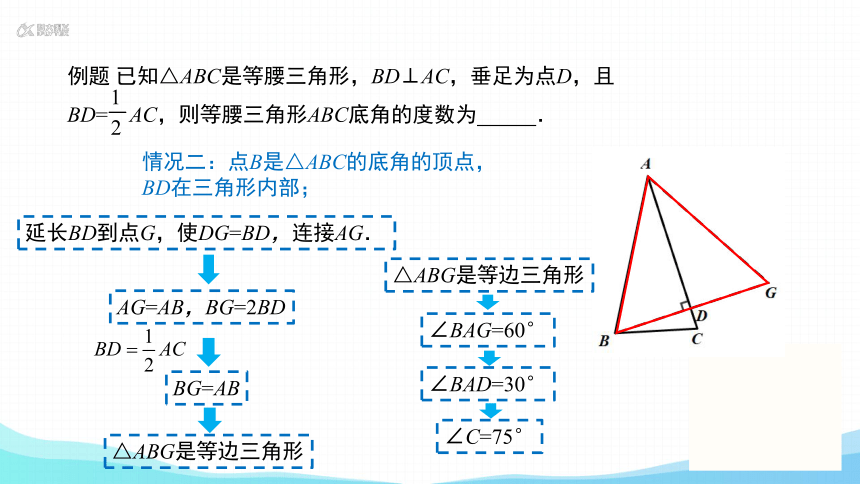
(2)点B是△ABC的底角的顶点,BD在三角形内部;
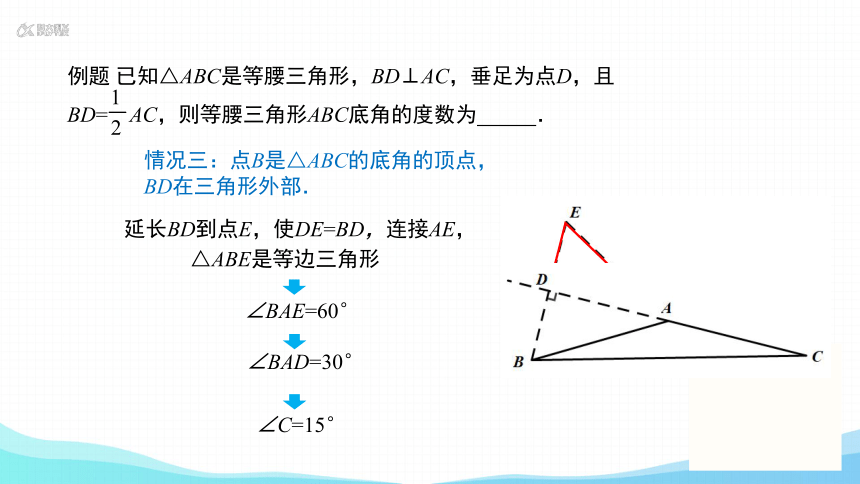
(3)点B是△ABC的底角的顶点,BD在三角形外部.
△ABC是钝角三角形
点B作为
底角顶点
AB=BC,BD⊥AC
BD=CD
∠C=45°
例题 已知△ABC是等腰三角形,BD⊥AC,垂足为点D,且
BD= AC,则等腰三角形ABC底角的度数为 .
情况一:点B是△ABC的顶角的顶点;
延长BD到点G,使DG=BD,连接AG.
AG=AB,BG=2BD
BG=AB
△ABG是等边三角形
情况二:点B是△ABC的底角的顶点, BD在三角形内部;
∠BAG=60°
△ABG是等边三角形
∠BAD=30°
∠C=75°
例题 已知△ABC是等腰三角形,BD⊥AC,垂足为点D,且
BD= AC,则等腰三角形ABC底角的度数为 .
延长BD到点E,使DE=BD,连接AE,
∠BAE=60°
∠BAD=30°
∠C=15°
△ABE是等边三角形
情况三:点B是△ABC的底角的顶点,BD在三角形外部.
例题 已知△ABC是等腰三角形,BD⊥AC,垂足为点D,且
BD= AC,则等腰三角形ABC底角的度数为 .
情况一:点B是△ABC的顶角的顶点;
解:∵AB=BC,BD⊥AC,
∴BD=CD.
∴∠C=45°.
∵BD= AC,
∴CD= AC,∠BDC=90 °.
∴∠CBD=∠C.
例题 已知△ABC是等腰三角形,BD⊥AC,垂足为点D,且
BD= AC,则等腰三角形ABC底角的度数为 .
45°
45°
解:延长BD到点G,使DG=BD,
连接AG.
∴BG=2BD.
∴BG=AC=AB=AG.
∴△ABG是等边三角形.
∵DG=BD= AC,BD⊥AC.
例题 已知△ABC是等腰三角形,BD⊥AC,垂足为点D,且
BD= AC,则等腰三角形ABC底角的度数为 .
情况二:点B是△ABC的底角的顶点, BD在三角形内部;
∴∠BAG=60°.
∴∠BAD=30°.
∵ BD⊥AC,
在△ABC中,
∵ AB=AC,
∴∠ABC=∠C.
又∠BAD+∠ABC+∠C=180°,
∴∠ABC=∠C=75°.
例题 已知△ABC是等腰三角形,BD⊥AC,垂足为点D,且
BD= AC,则等腰三角形ABC底角的度数为 .
综上所述:
∠C=45°
∠C=75°
∠C=15°
15°或45°或75°
小结:当题目中没有给出图形,根据已知条件所叙述的位置或数量关系,通过有条理的分析,画出对应图形,分情况进行讨论是解题的关键.
等腰三角形中角度或线段的证明
证明线段相等
线段中点
SSS,SAS,ASA,AAS,HL
全等三角形的对应边相等
角平分线上的点到角两边的距离相等
线段的垂直平分线上的点到线段两端点距离相等
等角对等边
例题 如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下四个结论:
①AE=CF ;
②△EPF是等腰直角三角形;
④当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合)BE+CF=EF.
上述结论中始终正确的有____________________.
①AE=CF;
AB=AC,∠BAC=90°
∠B=∠C=45°
点P是BC中点
AP⊥CP, ∠EAP= ∠FAP=45°
三线合一
例题 如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下四个结论:
∠EAP=∠FAP=∠C
∠APF+∠FPC=90°
∠EPF=90°
∠APF+∠EPA=90°
∠FPC=∠EPA
∠FAP=∠C
AP=CP
AP⊥CP
∠APC=90°
∠EPA =∠FPC
AP=CP
∠EAP=∠C
△AEP≌△CFP (ASA)
AE=CF
例题 如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下四个结论:
∴∠FPC=∠EPA.
∴∠APF+∠EPA= 90°.
∴∠B=∠C=45°.
∴∠EAP=∠C,∠FAP=∠C.
∴AE=CF.
∴∠APC=90°.
∵ AP⊥CP,
①AE=CF;
证明:∵AB=AC,∠BAC=90°,
∵点P是BC中点,
∴AP⊥CP,∠EAP=∠FAP=45°.
∴AP=CP.
例题 如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下四个结论:
∴∠APF+∠FPC=90°.
∵∠EPF=90°,
∴△AEP≌△CFP (ASA) .
在△AEP 与△CFP 中,
①正确
②△EPF是等腰直角三角形;
∵△AEP≌△CFP,
∴EP=FP.
∵∠EPF=90°,
∴△EPF是等腰直角三角形.
②正确
例题 如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下四个结论:
∵△AEP≌△CFP,
∴S△AEP =S△CFP .
∴S四边形AEPF= S△AEP + S△AFP =S△CFP + S△AFP.
∴S四边形AEPF=S△ACP .
∵
∴
③正确
例题 如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下四个结论:
④当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合)BE+CF=EF.
若BE+CF=EF,
例题 如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下四个结论:
则BE+AE=EF,即BA=EF,
△ABP与△EFP都是
等腰直角三角形
△ABP≌△EFP
EP=BP
点E不与A,B重合
EP≠BP
矛盾
④错误
AE=CF
①AE=CF;
②△EPF是等腰直角三角形;
④当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合)BE+CF=EF.
上述结论中始终正确的有____________________.
①②③
例题 如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下四个结论:
小结:
通过等腰三角形的性质可以得到三角形中线段或角的相等关系,而这些条件往往能够恰好得到全等三角形的条件,在解题过程中要注意挖掘这样的条件;
由于等腰直角三角形的特殊性,在遇到此类图形的时候要更加关注“直角”这个条件,深入思考图形中与之相关的条件.
例题 情景观察:如图1,在△ABC中,AB=AC,∠BAC=45°,CD⊥AB,AE⊥BC,垂足分别为D,E,CD与AE交于点F.
①写出图1中所有的全等三角形 ;
②线段AF与线段CE的数量关系是 ,并写出证明过程.
问题探究:如图2,在△ABC中,∠BAC=45°,AB=BC,AD平分∠BAC,AD⊥CD,垂足为D,AD与BC交于点E.
求证:AE=2CD.
图1
图2
例题 情景观察:如图1,在△ABC中,AB=AC,∠BAC=45°,CD⊥AB,AE⊥BC,垂足分别为D,E,CD与AE交于点F.
①写出图1中所有的全等三角形
;
图1
△ABE≌△ACE(HL)
分析:
△ADF≌△CDB(ASA)
△ABE≌△ACE,
△ADF≌△CDB
∴AD=CD.
△ADF≌△CDB
例题 情景观察:如图1,在△ABC中,AB=AC,∠BAC=45°,CD⊥AB,AE⊥BC,垂足分别为D,E,CD与AE交于点F.
②线段AF与线段CE的数量关系是 ,并写出证明过程.
AF=CB
CB=2CE
AF=2CE
图1
分析:
证明: ∵CD⊥AB,
∴∠ADC=∠CDB=90°.
∵∠BAC=45°,
∴∠ACD=∠BAC=45°.
图1
∵AE⊥BC,
∴∠AEB=90°.
∵∠CDB=90°,
∴∠DAE+∠B=90°.
∴∠DCB+∠B=90°.
∴∠DCB=∠DAE.
例题 情景观察:如图1,在△ABC中,AB=AC,∠BAC=45°,CD⊥AB,AE⊥BC,垂足分别为D,E,CD与AE交于点F.
②线段AF与线段CE的数量关系是 ,并写出证明过程.
AF=2CE
在△ADF 与△CDB中,
∴AF =CB.
∴△ADF≌△CDB(ASA).
∴AF=2CE.
∵AB=AC,AE⊥BC,
∴BC=2CE.
图1
例题 问题探究:如图2,在△ABC中,∠BAC=45°,AB=BC,AD平分∠BAC,AD⊥CD,垂足为D,AD与BC交于点E.
求证:AE=2CD.
构造全等三角形
延长AB,CD
图2
分析:
证明:延长AB,CD交于点F,
∴∠ADF=∠ADC =90°.
∵AD平分∠BAC,
∴∠BAD=∠CAD.
∵AD=AD.
∵AD⊥CD,
∴△FAD≌△CAD(ASA).
在△FAD与△CAD中,
∵AB=BC, ∠BAC=45°
∴∠BAD+∠F=90°.
∵∠ADF=90°.
∴∠BAC=∠BCA =45°.
∴∠ABC=∠CBF=90°.
∴∠BCF+∠F=90°.
∴FD=CD.
∴FC=2CD.
∴∠BAD=∠BCF.
例题 问题探究:如图2,在△ABC中,∠BAC=45°,AB=BC,AD平分∠BAC,AD⊥CD,垂足为D,AD与BC交于点E.
求证:AE=2CD.
图2
在△ABE 与△CBF中,
∴AE =CF.
∴△ABE≌△CBF(ASA).
∴AE=2CD.
小结:等腰三角形中的两腰往往可以分别放在另外两个不同的三角形中,作为全等三角形的一组关于边相等的条件,再加上其他的边、角的关系,通过全等,证明未知线段或角的关系.
又 CF=2CD,
旋转产生的等腰问题
1.有两边相等的三角形是等腰三角形;
2.图形绕某点旋转一定角度后,对应线段相等,对应线段旋转的角度也相等.
基本图形1:
当线段OA绕着端点O进行旋转,旋转角度是α,
则有OA=OB,连接AB,得到△OAB是等腰三角形.
1.有两边相等的三角形是等腰三角形;
2.图形绕某点旋转一定角度后,对应线段相等,对应线段旋转的角度也相等.
基本图形2:
当△ABC绕着顶点A旋转α°,
则可以得到△ABC≌△ADE:AB=AD,AC=AE,BC=DE;
连接BD,得到△ABD是等腰三角形;
连接CE,得到△ACE是等腰三角形.
例题 如图,△ABC是等腰三角形,AB=AC,∠BAC=45°,点D在AC边上,将△ABD绕点A逆时针旋转45°得到△ACD′,且点D′,D,B三点在同一条直线上,则∠ABD的度数是 .
AD=AD′
∠ADD′ =∠AD′D
求∠AD′D
求∠ABD
△ABD绕点A逆时针旋转
分析:
例题 如图,△ABC是等腰三角形,AB=AC,∠BAC=45°,点D在AC边上,将△ABD绕点A逆时针旋转45°得到△ACD′,且点D′,D,B三点在同一条直线上,则∠ABD的度数是 .
解:由旋转得AD =AD′,
∴∠ADD′=∠AD′D.
∵∠DAD′=∠DAB=45° ,
∴∠ADD′=∠AD′D =67.5°.
∵∠DAB=45° ,
∴∠BAD′ =90°.
∴∠ABD= 90°- 67.5°=22.5°.
小结:由旋转前后共端点的相等线段得到等腰三角形,根据等边对等角得到两个底角相等,旋转角作为顶角度数是已知条件,根据三角形内角和求出底角的度数.
例题 如图,在△ABC中,CA=CB,∠ACB=60°.点P是平面内不与点A,C重合的任意一点.连接AP,将线段AP绕点P逆时针旋转60°得到线段DP,连接AD,BD,CP.
(1)求证:BD=CP;
(2)求直线BD与直线CP相交形成的较小角的度数.
等边三角形
分析:
CA=CB,∠ACB=60°
△ABC是等边三角形
AC =AB,∠CAB=60°
AP=AD,∠PAD=60°
旋转60°
线段AP绕点P逆时针旋转
AP=DP
△PAD是等边三角形.
∠CAB=∠PAD
∠CAP=∠BAD
△CAP≌△BAD(SAS).
BD=CP.
证明:∵CA=CB ,∠ACB=60°
∴△ABC是等边三角形
∴AC =AB,∠CAB=60°
∵AP=DP,∠APD=60°
∴AP =AD,∠PAD=60°
∴△PAD是等边三角形
例题 如图,在△ABC中,CA=CB,∠ACB=60°.点P是平面内不与点A,C重合的任意一点.连接AP,将线段AP绕点P逆时针旋转60°得到线段DP,连接AD,BD,CP.
(1)求证:BD=CP;
∴∠CAB=∠PAD.
∴△CAP≌△BAD(SAS).
∴BD=CP.
∴∠CAB-∠PAB=∠PAD-∠PAB.
∴∠CAP=∠BAD.
解:延长CP,BD交于点G,
∵△CAP≌△BAD,
∴∠1=∠2.
1
2
在△GBC中,
∠GCB+∠CBG= ∠GCB+∠ 2 +∠ABC.
例题 如图,在△ABC中,CA=CB,∠ACB=60°.点P是平面内不与点A,C重合的任意一点.连接AP,将线段AP绕点P逆时针旋转60°得到线段DP,连接AD,BD,CP.
(2)求直线BD与直线CP相交形成的较小角的度数.
∵△ABC是等边三角形,
∴∠ACB+∠ABC=120°
∴∠CGB=60°
G
60°
= ∠GCB+∠ 1 +∠ABC.
= ∠ACB+∠ABC.
小结:旋转前后的两条线段相等,如果旋转角是60°,则可以得到等边三角形.找到结论中两条线段所在的两个三角形的全等的条件是解题的关键.
等腰三角形中的计算或证明
角度,利用等边对等角,三角形内角和定理知一求二;
线段,利用等腰三角形的轴对称性得到相等的线段;
直接通过等边对等角构造全等三角形的条件;
通过三线合一性质挖掘题目中存在的线段或角之间的数量关系;
抓住旋转变换中共端点的相等线段发现题目中隐含的等腰三角形,再应用等腰三角形的性质进行分析.
计算
证明
旋转中的等腰问题
再 见
沪科版八年级上册数学
等腰三角形的计算或证明
等腰三角形中角度或线段的相关计算
等腰三角形
定义
性质
判定
分类
有两条边相等的三角形是等腰三角形;
等边对等角;“三线合一”;
两边相等(定义);等角对等边;
一般的等腰三角形
等腰直角三角形(顶角是90°)
等边三角形(底边与腰相等)
边角计算
分类讨论
三条边都相等
三个角都相等(60°)
例题 如图,△ABC是等腰三角形,AB=AC,∠BAC=80°,AD平分∠BAC,
且AD=AE,求∠EDC的度数.
分析:
△ABC是等腰三角形,
AB=AC,AD平分∠BAC
三线合一
AD⊥BC
∠ADC=90°
∠ADE=70°
AD平分∠BAC,
∠BAC=80°
AD=AE
∠ADE=∠AED
∠DAE=40°
∠EDC=20°
解:
∵ △ABC是等腰三角形,
AB=AC ,
AD平分∠BAC ,
∴ AD⊥BC.
∴∠ADC=90°.
在△ADE中,
∵ AD=AE,
∴∠ADE=∠AED.
∴∠EDC=∠ADC -∠ADE=20°.
∵∠BAC=80°,
∴∠DAE=40°.
∵∠ADE+∠AED+∠DAE=180°.
∴2∠ADE+40°=180 °.
∴∠ADE=70°.
小结:由等腰三角形顶角的平分线可以推出底边上的高进而得到直角,同时可以找到顶角的一半的度数;依据等边对等角,可以找到等腰三角形中相等的角,知一求二得到三角形每个角的度数.对于求角度的题目,在解题中需要寻求跟求角度相关的条件.
例题 如图,△ABC是等腰三角形,AB=AC,∠BAC=80°,AD平分∠BAC,
且AD=AE,求∠EDC的度数.
70°
20°
例题 如图, △ABC是等边三角形,AD是BC边上的中线,且AD=4,E,P分别是AC,AD上的动点,则CP+EP的最小值等于 .
等边三角形具有轴对称性
CP=BP
CP+EP
BP+EP
BP+EP的最小值
BE的长
两点之间,
线段最短
分析:
BE的最小值
点到直线的距离
——垂线段的长度
过点B作AC的垂线段
例题 如图, △ABC是等边三角形,AD是BC边上的中线,且AD=4,E,P分别是AC,AD上的动点,则CP+EP的最小值等于 .
AD是BC边上的中线,
∴AD⊥BC.
∴CP+EP的最小值等于4.
小结:等边三角形具有轴对称性,根据轴对称性构图可以将两条线段之和的问题转化为两点之间线段最短的问题求解,而连接三角形一个顶点到对边上各个点的所有线段中,垂线段最短.
解:
∵△ABC是等边三角形,
∴过点B作BE’⊥AC于点E’.
∵AD=BE’且AD=4.
∴ BE’=4.
∴点C与点B关于直线AD对称
∴CP =BP.
∴CP+EP=BP+PE.
当CP+EP取最小值时,B,P,E三点在同一直线上,且当BE⊥AC时,BE最短.
4
连接BP.
例题 已知△ABC是等腰三角形,BD⊥AC,垂足为点D,且
BD= AC,则等腰三角形ABC底角的度数为 .
BD⊥AC
点B作为
顶角顶点
△ABC是锐角三角形
分析:
所以共分三种情况:
(1)点B是△ABC的顶角的顶点;
(2)点B是△ABC的底角的顶点,BD在三角形内部;
(3)点B是△ABC的底角的顶点,BD在三角形外部.
△ABC是钝角三角形
点B作为
底角顶点
AB=BC,BD⊥AC
BD=CD
∠C=45°
例题 已知△ABC是等腰三角形,BD⊥AC,垂足为点D,且
BD= AC,则等腰三角形ABC底角的度数为 .
情况一:点B是△ABC的顶角的顶点;
延长BD到点G,使DG=BD,连接AG.
AG=AB,BG=2BD
BG=AB
△ABG是等边三角形
情况二:点B是△ABC的底角的顶点, BD在三角形内部;
∠BAG=60°
△ABG是等边三角形
∠BAD=30°
∠C=75°
例题 已知△ABC是等腰三角形,BD⊥AC,垂足为点D,且
BD= AC,则等腰三角形ABC底角的度数为 .
延长BD到点E,使DE=BD,连接AE,
∠BAE=60°
∠BAD=30°
∠C=15°
△ABE是等边三角形
情况三:点B是△ABC的底角的顶点,BD在三角形外部.
例题 已知△ABC是等腰三角形,BD⊥AC,垂足为点D,且
BD= AC,则等腰三角形ABC底角的度数为 .
情况一:点B是△ABC的顶角的顶点;
解:∵AB=BC,BD⊥AC,
∴BD=CD.
∴∠C=45°.
∵BD= AC,
∴CD= AC,∠BDC=90 °.
∴∠CBD=∠C.
例题 已知△ABC是等腰三角形,BD⊥AC,垂足为点D,且
BD= AC,则等腰三角形ABC底角的度数为 .
45°
45°
解:延长BD到点G,使DG=BD,
连接AG.
∴BG=2BD.
∴BG=AC=AB=AG.
∴△ABG是等边三角形.
∵DG=BD= AC,BD⊥AC.
例题 已知△ABC是等腰三角形,BD⊥AC,垂足为点D,且
BD= AC,则等腰三角形ABC底角的度数为 .
情况二:点B是△ABC的底角的顶点, BD在三角形内部;
∴∠BAG=60°.
∴∠BAD=30°.
∵ BD⊥AC,
在△ABC中,
∵ AB=AC,
∴∠ABC=∠C.
又∠BAD+∠ABC+∠C=180°,
∴∠ABC=∠C=75°.
例题 已知△ABC是等腰三角形,BD⊥AC,垂足为点D,且
BD= AC,则等腰三角形ABC底角的度数为 .
综上所述:
∠C=45°
∠C=75°
∠C=15°
15°或45°或75°
小结:当题目中没有给出图形,根据已知条件所叙述的位置或数量关系,通过有条理的分析,画出对应图形,分情况进行讨论是解题的关键.
等腰三角形中角度或线段的证明
证明线段相等
线段中点
SSS,SAS,ASA,AAS,HL
全等三角形的对应边相等
角平分线上的点到角两边的距离相等
线段的垂直平分线上的点到线段两端点距离相等
等角对等边
例题 如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下四个结论:
①AE=CF ;
②△EPF是等腰直角三角形;
④当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合)BE+CF=EF.
上述结论中始终正确的有____________________.
①AE=CF;
AB=AC,∠BAC=90°
∠B=∠C=45°
点P是BC中点
AP⊥CP, ∠EAP= ∠FAP=45°
三线合一
例题 如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下四个结论:
∠EAP=∠FAP=∠C
∠APF+∠FPC=90°
∠EPF=90°
∠APF+∠EPA=90°
∠FPC=∠EPA
∠FAP=∠C
AP=CP
AP⊥CP
∠APC=90°
∠EPA =∠FPC
AP=CP
∠EAP=∠C
△AEP≌△CFP (ASA)
AE=CF
例题 如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下四个结论:
∴∠FPC=∠EPA.
∴∠APF+∠EPA= 90°.
∴∠B=∠C=45°.
∴∠EAP=∠C,∠FAP=∠C.
∴AE=CF.
∴∠APC=90°.
∵ AP⊥CP,
①AE=CF;
证明:∵AB=AC,∠BAC=90°,
∵点P是BC中点,
∴AP⊥CP,∠EAP=∠FAP=45°.
∴AP=CP.
例题 如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下四个结论:
∴∠APF+∠FPC=90°.
∵∠EPF=90°,
∴△AEP≌△CFP (ASA) .
在△AEP 与△CFP 中,
①正确
②△EPF是等腰直角三角形;
∵△AEP≌△CFP,
∴EP=FP.
∵∠EPF=90°,
∴△EPF是等腰直角三角形.
②正确
例题 如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下四个结论:
∵△AEP≌△CFP,
∴S△AEP =S△CFP .
∴S四边形AEPF= S△AEP + S△AFP =S△CFP + S△AFP.
∴S四边形AEPF=S△ACP .
∵
∴
③正确
例题 如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下四个结论:
④当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合)BE+CF=EF.
若BE+CF=EF,
例题 如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下四个结论:
则BE+AE=EF,即BA=EF,
△ABP与△EFP都是
等腰直角三角形
△ABP≌△EFP
EP=BP
点E不与A,B重合
EP≠BP
矛盾
④错误
AE=CF
①AE=CF;
②△EPF是等腰直角三角形;
④当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合)BE+CF=EF.
上述结论中始终正确的有____________________.
①②③
例题 如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下四个结论:
小结:
通过等腰三角形的性质可以得到三角形中线段或角的相等关系,而这些条件往往能够恰好得到全等三角形的条件,在解题过程中要注意挖掘这样的条件;
由于等腰直角三角形的特殊性,在遇到此类图形的时候要更加关注“直角”这个条件,深入思考图形中与之相关的条件.
例题 情景观察:如图1,在△ABC中,AB=AC,∠BAC=45°,CD⊥AB,AE⊥BC,垂足分别为D,E,CD与AE交于点F.
①写出图1中所有的全等三角形 ;
②线段AF与线段CE的数量关系是 ,并写出证明过程.
问题探究:如图2,在△ABC中,∠BAC=45°,AB=BC,AD平分∠BAC,AD⊥CD,垂足为D,AD与BC交于点E.
求证:AE=2CD.
图1
图2
例题 情景观察:如图1,在△ABC中,AB=AC,∠BAC=45°,CD⊥AB,AE⊥BC,垂足分别为D,E,CD与AE交于点F.
①写出图1中所有的全等三角形
;
图1
△ABE≌△ACE(HL)
分析:
△ADF≌△CDB(ASA)
△ABE≌△ACE,
△ADF≌△CDB
∴AD=CD.
△ADF≌△CDB
例题 情景观察:如图1,在△ABC中,AB=AC,∠BAC=45°,CD⊥AB,AE⊥BC,垂足分别为D,E,CD与AE交于点F.
②线段AF与线段CE的数量关系是 ,并写出证明过程.
AF=CB
CB=2CE
AF=2CE
图1
分析:
证明: ∵CD⊥AB,
∴∠ADC=∠CDB=90°.
∵∠BAC=45°,
∴∠ACD=∠BAC=45°.
图1
∵AE⊥BC,
∴∠AEB=90°.
∵∠CDB=90°,
∴∠DAE+∠B=90°.
∴∠DCB+∠B=90°.
∴∠DCB=∠DAE.
例题 情景观察:如图1,在△ABC中,AB=AC,∠BAC=45°,CD⊥AB,AE⊥BC,垂足分别为D,E,CD与AE交于点F.
②线段AF与线段CE的数量关系是 ,并写出证明过程.
AF=2CE
在△ADF 与△CDB中,
∴AF =CB.
∴△ADF≌△CDB(ASA).
∴AF=2CE.
∵AB=AC,AE⊥BC,
∴BC=2CE.
图1
例题 问题探究:如图2,在△ABC中,∠BAC=45°,AB=BC,AD平分∠BAC,AD⊥CD,垂足为D,AD与BC交于点E.
求证:AE=2CD.
构造全等三角形
延长AB,CD
图2
分析:
证明:延长AB,CD交于点F,
∴∠ADF=∠ADC =90°.
∵AD平分∠BAC,
∴∠BAD=∠CAD.
∵AD=AD.
∵AD⊥CD,
∴△FAD≌△CAD(ASA).
在△FAD与△CAD中,
∵AB=BC, ∠BAC=45°
∴∠BAD+∠F=90°.
∵∠ADF=90°.
∴∠BAC=∠BCA =45°.
∴∠ABC=∠CBF=90°.
∴∠BCF+∠F=90°.
∴FD=CD.
∴FC=2CD.
∴∠BAD=∠BCF.
例题 问题探究:如图2,在△ABC中,∠BAC=45°,AB=BC,AD平分∠BAC,AD⊥CD,垂足为D,AD与BC交于点E.
求证:AE=2CD.
图2
在△ABE 与△CBF中,
∴AE =CF.
∴△ABE≌△CBF(ASA).
∴AE=2CD.
小结:等腰三角形中的两腰往往可以分别放在另外两个不同的三角形中,作为全等三角形的一组关于边相等的条件,再加上其他的边、角的关系,通过全等,证明未知线段或角的关系.
又 CF=2CD,
旋转产生的等腰问题
1.有两边相等的三角形是等腰三角形;
2.图形绕某点旋转一定角度后,对应线段相等,对应线段旋转的角度也相等.
基本图形1:
当线段OA绕着端点O进行旋转,旋转角度是α,
则有OA=OB,连接AB,得到△OAB是等腰三角形.
1.有两边相等的三角形是等腰三角形;
2.图形绕某点旋转一定角度后,对应线段相等,对应线段旋转的角度也相等.
基本图形2:
当△ABC绕着顶点A旋转α°,
则可以得到△ABC≌△ADE:AB=AD,AC=AE,BC=DE;
连接BD,得到△ABD是等腰三角形;
连接CE,得到△ACE是等腰三角形.
例题 如图,△ABC是等腰三角形,AB=AC,∠BAC=45°,点D在AC边上,将△ABD绕点A逆时针旋转45°得到△ACD′,且点D′,D,B三点在同一条直线上,则∠ABD的度数是 .
AD=AD′
∠ADD′ =∠AD′D
求∠AD′D
求∠ABD
△ABD绕点A逆时针旋转
分析:
例题 如图,△ABC是等腰三角形,AB=AC,∠BAC=45°,点D在AC边上,将△ABD绕点A逆时针旋转45°得到△ACD′,且点D′,D,B三点在同一条直线上,则∠ABD的度数是 .
解:由旋转得AD =AD′,
∴∠ADD′=∠AD′D.
∵∠DAD′=∠DAB=45° ,
∴∠ADD′=∠AD′D =67.5°.
∵∠DAB=45° ,
∴∠BAD′ =90°.
∴∠ABD= 90°- 67.5°=22.5°.
小结:由旋转前后共端点的相等线段得到等腰三角形,根据等边对等角得到两个底角相等,旋转角作为顶角度数是已知条件,根据三角形内角和求出底角的度数.
例题 如图,在△ABC中,CA=CB,∠ACB=60°.点P是平面内不与点A,C重合的任意一点.连接AP,将线段AP绕点P逆时针旋转60°得到线段DP,连接AD,BD,CP.
(1)求证:BD=CP;
(2)求直线BD与直线CP相交形成的较小角的度数.
等边三角形
分析:
CA=CB,∠ACB=60°
△ABC是等边三角形
AC =AB,∠CAB=60°
AP=AD,∠PAD=60°
旋转60°
线段AP绕点P逆时针旋转
AP=DP
△PAD是等边三角形.
∠CAB=∠PAD
∠CAP=∠BAD
△CAP≌△BAD(SAS).
BD=CP.
证明:∵CA=CB ,∠ACB=60°
∴△ABC是等边三角形
∴AC =AB,∠CAB=60°
∵AP=DP,∠APD=60°
∴AP =AD,∠PAD=60°
∴△PAD是等边三角形
例题 如图,在△ABC中,CA=CB,∠ACB=60°.点P是平面内不与点A,C重合的任意一点.连接AP,将线段AP绕点P逆时针旋转60°得到线段DP,连接AD,BD,CP.
(1)求证:BD=CP;
∴∠CAB=∠PAD.
∴△CAP≌△BAD(SAS).
∴BD=CP.
∴∠CAB-∠PAB=∠PAD-∠PAB.
∴∠CAP=∠BAD.
解:延长CP,BD交于点G,
∵△CAP≌△BAD,
∴∠1=∠2.
1
2
在△GBC中,
∠GCB+∠CBG= ∠GCB+∠ 2 +∠ABC.
例题 如图,在△ABC中,CA=CB,∠ACB=60°.点P是平面内不与点A,C重合的任意一点.连接AP,将线段AP绕点P逆时针旋转60°得到线段DP,连接AD,BD,CP.
(2)求直线BD与直线CP相交形成的较小角的度数.
∵△ABC是等边三角形,
∴∠ACB+∠ABC=120°
∴∠CGB=60°
G
60°
= ∠GCB+∠ 1 +∠ABC.
= ∠ACB+∠ABC.
小结:旋转前后的两条线段相等,如果旋转角是60°,则可以得到等边三角形.找到结论中两条线段所在的两个三角形的全等的条件是解题的关键.
等腰三角形中的计算或证明
角度,利用等边对等角,三角形内角和定理知一求二;
线段,利用等腰三角形的轴对称性得到相等的线段;
直接通过等边对等角构造全等三角形的条件;
通过三线合一性质挖掘题目中存在的线段或角之间的数量关系;
抓住旋转变换中共端点的相等线段发现题目中隐含的等腰三角形,再应用等腰三角形的性质进行分析.
计算
证明
旋转中的等腰问题
再 见
