15.2线段的垂直平分线-线段垂直平分线的应用 课件(共37张PPT) 2023--2024学年沪科版八年级数学上册
文档属性
| 名称 | 15.2线段的垂直平分线-线段垂直平分线的应用 课件(共37张PPT) 2023--2024学年沪科版八年级数学上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 707.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-14 22:09:42 | ||
图片预览



文档简介
(共37张PPT)
沪科版八年级上册数学
线段垂直平分线的应用
判断线段垂直平分线
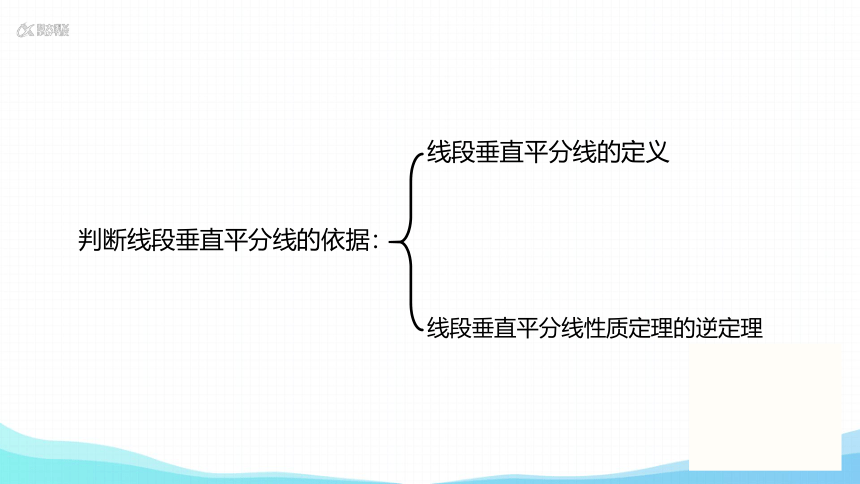
判断线段垂直平分线的依据:
线段垂直平分线的定义
线段垂直平分线性质定理的逆定理
线段垂直平分线的定义
经过线段中点,并且垂直于这条线段的直线,叫做这条线段的垂直平分线
直线 l⊥AB,AC=BC
直线 l 垂直平分线段AB
A
B
C
l
中点
垂直
,又称“中垂线”.
方法归纳:若已知一条直线经过线段的中点并且垂直这条线段,则根据垂直平分线的定义,即可判断直线是线段的垂直平分线.
线段垂直平分线性质定理的逆定理
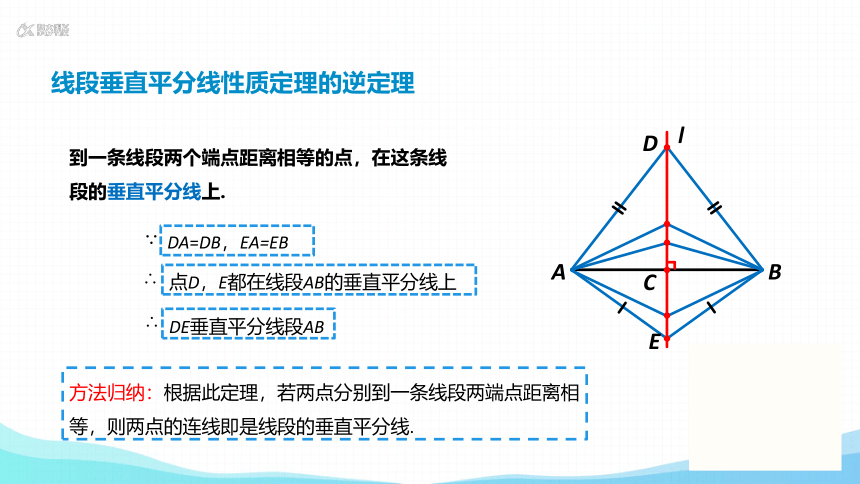
到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
A
B
C
DA=DB,EA=EB
DE垂直平分线段AB
l
D
E
方法归纳:根据此定理,若两点分别到一条线段两端点距离相等,则两点的连线即是线段的垂直平分线.
点D,E都在线段AB的垂直平分线上
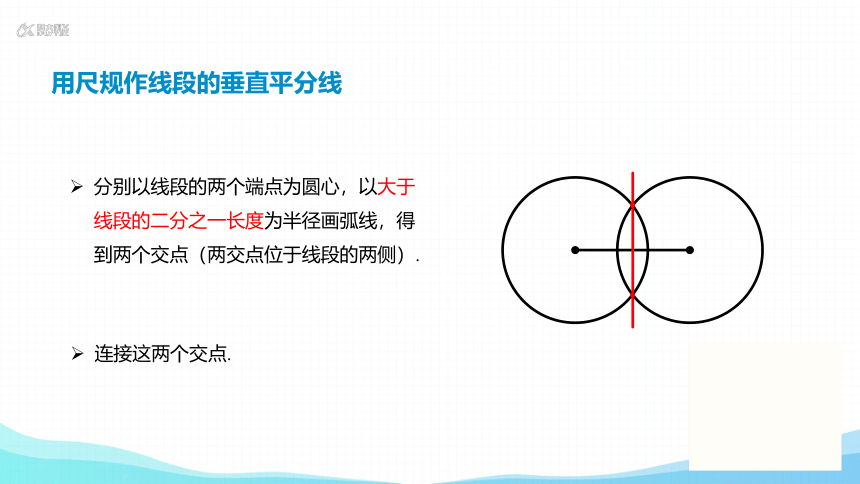
分别以线段的两个端点为圆心,以大于线段的二分之一长度为半径画弧线,得到两个交点(两交点位于线段的两侧).
连接这两个交点.
用尺规作线段的垂直平分线
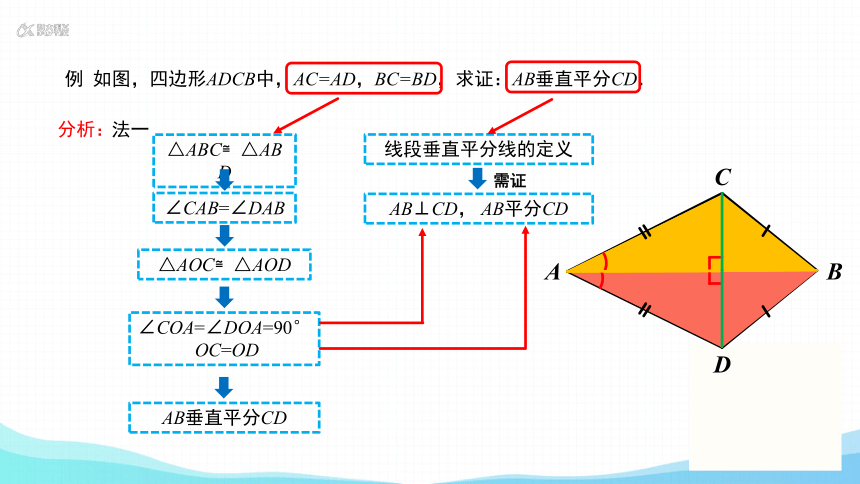
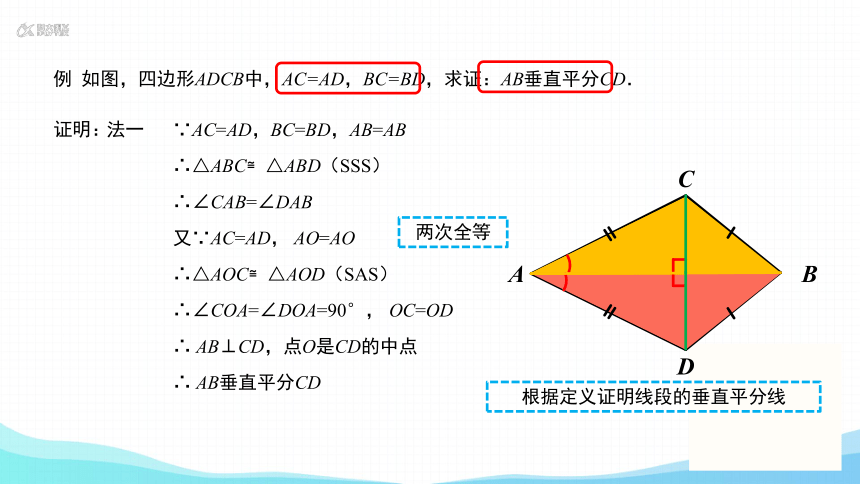
例 如图,四边形ADCB中,AC=AD,BC=BD,求证:AB垂直平分CD.
A
B
C
D
O
法一
△ABC≌△ABD
∠CAB=∠DAB
△AOC≌△AOD
∠COA=∠DOA=90°
OC=OD
AB垂直平分CD
分析:
线段垂直平分线的定义
AB⊥CD, AB平分CD
需证
例 如图,四边形ADCB中,AC=AD,BC=BD,求证:AB垂直平分CD.
法一
证明:
∵AC=AD,BC=BD,AB=AB
∴△ABC≌△ABD(SSS)
∴∠CAB=∠DAB
又∵AC=AD, AO=AO
∴△AOC≌△AOD(SAS)
∴∠COA=∠DOA=90°, OC=OD
∴ AB⊥CD,点O是CD的中点
∴ AB垂直平分CD
A
B
C
D
O
两次全等
根据定义证明线段的垂直平分线
(SSS)
(SAS)
例 如图,四边形ADCB中,AC=AD,BC=BD,求证:AB垂直平分CD.
A
B
C
D
O
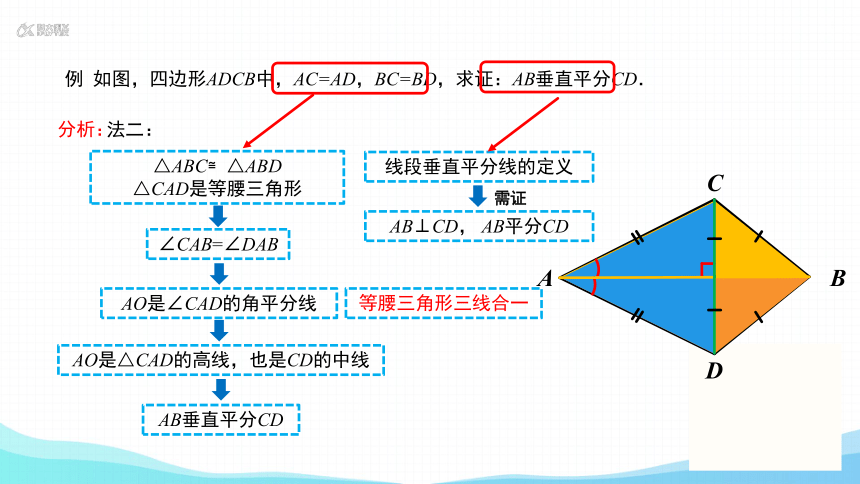
法二:
△ABC≌△ABD
△CAD是等腰三角形
∠CAB=∠DAB
AO是∠CAD的角平分线
AO是△CAD的高线,也是CD的中线
AB垂直平分CD
分析:
线段垂直平分线的定义
AB⊥CD, AB平分CD
需证
等腰三角形三线合一
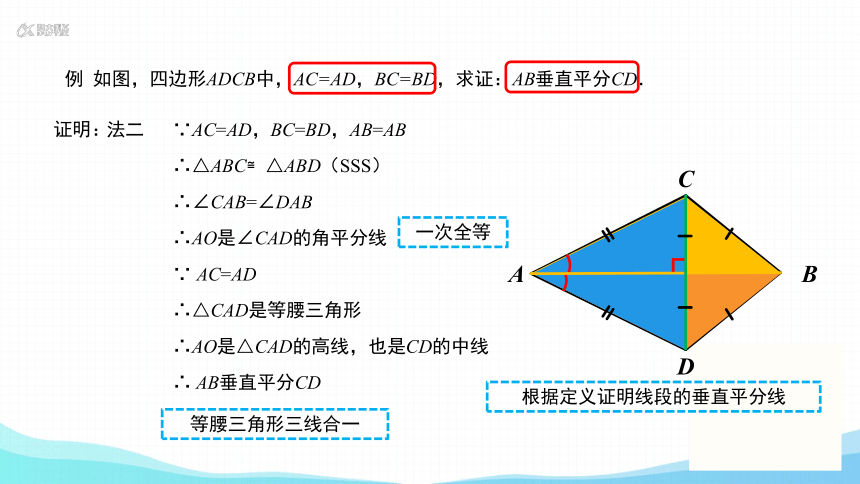
例 如图,四边形ADCB中,AC=AD,BC=BD,求证:AB垂直平分CD.
法二
∵AC=AD,BC=BD,AB=AB
∴△ABC≌△ABD(SSS)
∴∠CAB=∠DAB
∴AO是∠CAD的角平分线
∵ AC=AD
∴△CAD是等腰三角形
∴AO是△CAD的高线,也是CD的中线
∴ AB垂直平分CD
A
B
C
D
O
证明:
一次全等
等腰三角形三线合一
根据定义证明线段的垂直平分线
A
B
C
D
O
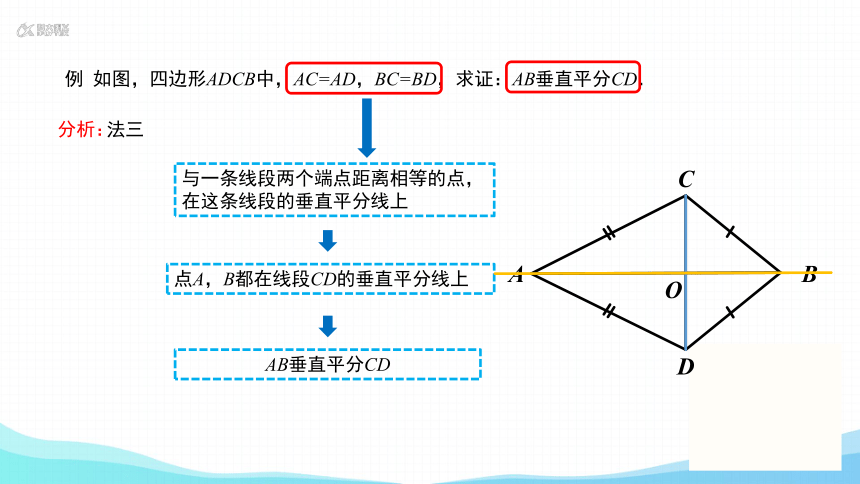
例 如图,四边形ADCB中,AC=AD,BC=BD,求证:AB垂直平分CD.
法三
与一条线段两个端点距离相等的点,
在这条线段的垂直平分线上
点A,B都在线段CD的垂直平分线上
分析:
AB垂直平分CD
A
B
C
D
O
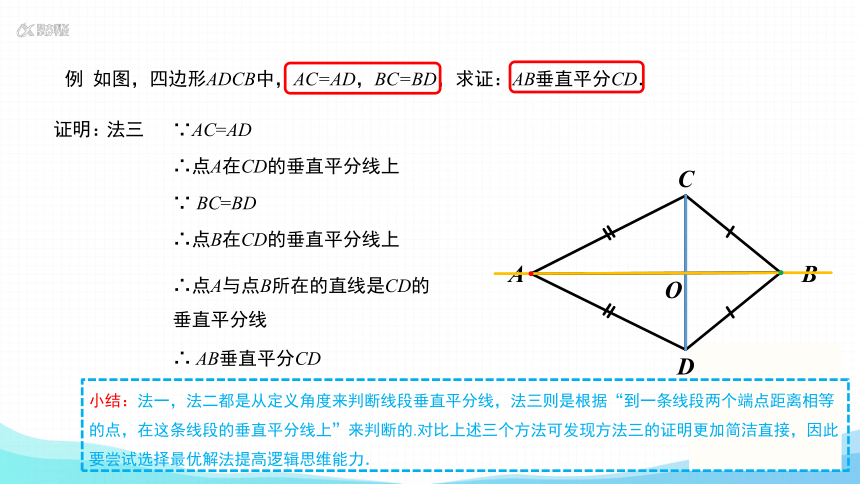
例 如图,四边形ADCB中,AC=AD,BC=BD,求证:AB垂直平分CD.
法三
∵AC=AD
∴点A在CD的垂直平分线上
∵ BC=BD
∴点B在CD的垂直平分线上
∴点A与点B所在的直线是CD的垂直平分线
∴ AB垂直平分CD
证明:
小结:法一,法二都是从定义角度来判断线段垂直平分线,法三则是根据“到一条线段两个端点距离相等的点,在这条线段的垂直平分线上”来判断的.对比上述三个方法可发现方法三的证明更加简洁直接,因此要尝试选择最优解法提高逻辑思维能力.
例 如图,电信部门要在S区建一座信号发射塔.按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条高速公路m,n的距离也必须相等.发射塔应修建在什么位置?在图上标出它的位置.
A
B
O
S
m
n
到一条线段两个端点距离相等的点,在这条线段的垂直平分线上
到角两边距离相等的点在角的平分线上
发射塔在线段AB的垂直平分线和m与n夹角的角平分线的交点处
连接点A,点B,发射塔在线段AB的垂直平分线上
发射塔在m与n夹角的角平分线上
分析:
例 如图,电信部门要在S区建一座信号发射塔.按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条高速公路m,n的距离也必须相等.发射塔应修建在什么位置?在图上标出它的位置.
A
B
O
S
m
n
解:
连接AB
因为到一条线段两个端点距离相等的点,在这条线段的垂直平分线上,所以:
分别以线段的两个端点为圆心,以大于线段的二分之一长度为半径画圆
得到两个交点
连接这两个交点
到一条线段两个端点距离相等的点,在这条线段的垂直平分线上
例 如图,电信部门要在S区建一座信号发射塔.按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条高速公路m,n的距离也必须相等.发射塔应修建在什么位置?在图上标出它的位置.
A
B
O
S
m
n
因为到角两边距离相等的点在角的平分线上
所以:以点O为圆心,以任意长为半径画圆,分别交直线m,n于点M,N.
分别以点M,N为圆心,以大于 MN的长度为半径画圆, 两圆交于点P.
作射线OP
M
N
P
C
∠MON的角平分线与AB的垂直平分线相交于点C
发射塔应修建在点C,点C到A,B距离相等,到直线m,n的距离也相等.
解:
到角两边距离相等的点在角的平分线上
小结:熟练掌握利用尺规作角的平分线及线段的垂直平分线是解题的关键.
求线段之间的关系
添加环节P
求线段之间的关系:
求线段长或线段之间的数量关系
探究线段位置关系
直线 l 垂直平分线段AB
线段垂直平分线的性质
线段垂直平分线上的点到这条线段两个端点的距离相等.
A
B
C
l
D
DA=DB
线段垂直平分线的性质
直线 l 垂直平分线段AB
DC⊥AB,BC=AC
点C是线段AB的中点
DC是等腰△DAB的高、中线
DA=DB
△DAB是等腰三角形
A
B
C
l
D
线段的特殊位置关系
平行∥
垂直⊥
例 如图,AD⊥BC,BD=CD,点C在AE的垂直平分线上,若AB=5cm,BD=3cm.求BE的长.
A
B
C
D
E
AD垂直平分BC
AB=AC
AC=EC
AB=AC=EC=5cm
BD=CD=3cm
BE=BD+CD+EC=11cm
5cm
3cm
3cm
分析:
例 如图,AD⊥BC,BD=CD,点C在AE的垂直平分线上,若AB=5cm,BD=3cm.求BE的长.
A
B
C
D
E
5cm
3cm
3cm
∵ AD⊥BC,BD=CD
∴AD所在的直线是BC的垂直平分线
∴ AB=AC
又∵点C在AE的垂直平分线上
∴AC=EC
∴ AB=AC=EC=5cm
又BD=CD=3cm
∴BE=BD+CD+EC=11cm
解:
小结:
首先,利用垂直平分线的定义判定线段的垂直平分线;
其次,根据点在垂直平分线上,得到线段相等的关系;
最后,进行线段长度的计算.
例 如图,在D,E分别是线段AB,AC的中点,CD⊥AB,垂足为D,BE⊥AC,垂足为E.求证:AC=AB.
A
B
C
D
E
连接BC
D是线段AB的中点且CD⊥AB
AC=BC
E是线段AC的中点且BE⊥AC
AB=BC
AC=AB
分析:
CD是线段AB的垂直平分线
BE是线段AC的垂直平分线
例 如图,在D,E分别是线段AB,AC的中点,CD⊥AB,垂足为D,BE⊥AC,垂足为E.求证:AC=AB.
A
B
C
D
E
连接BC
∵ 点D是线段AB的中点且CD⊥AB
∴ AC=BC
又∵点E是线段AC的中点且BE⊥AC
∴AB=BC
∴ AC=BC=AB
∴AC=AB
证明:
小结:利用线段垂直平分线的性质得出对应线段相等,再进行等量代换是解决此题的关键.
∴ CD是线段AB的垂直平分线
∴ BE是线段AC的垂直平分线
例 如图,在△ABC中,AD是∠BAC的平分线,DE,DF分别是△ABD和△ACD的高.试猜想:AD与EF之间有什么位置关系?请证明你的猜想.
A
B
C
D
E
F
DE⊥AB,DF⊥AC
AD是公共边
Rt△ADE≌ Rt△ADF(HL)
AE=AF
AD垂直平分EF
分析:
DE=DF
AD是∠BAC的平分线
例 如图,在△ABC中,AD是∠BAC的平分线,DE,DF分别是△ABD和△ACD的高.试猜想:AD与EF之间有什么位置关系?请证明你的猜想.
∵ DE,DF分别是△ABD和△ACD的高,
∴ DE⊥AB,DF⊥AC,
∵ AD是∠BAC的平分线,
∴ DE=DF,
又∵AD是公共边,DE=DF
∴ Rt△ADE≌ Rt△ADF(HL),
A
B
C
D
E
F
∴ AE=AF,
∴ AD垂直平分EF.
猜想:AD垂直平分EF.
证明:
小结: 探究两条线段的位置关系时,先猜想垂直平分的关系,再根据已知条件来进行推理证明.
∴点A在线段EF的垂直平分线上
∴点D都在线段EF的垂直平分线上
求角的度数
求角的度数
从定义角度:垂直
从性质角度:等边对等角
求角的度数
引例
A
B
C
D
如图,AD垂直平分线段BC
则AD⊥BC,BD=CD,
则AB=AC,
∠ADB=∠ADC=90°
∠B=∠C
定义角度
性质角度
角的关系
例 如图,在Rt △ABC中,∠B=90°,ED是AC的垂直平分线,交AC于点D,交BC于点E.已知∠BAE=16°,那么∠C的度数是多少?
A
B
C
D
E
ED是AC的垂直平分线
AE=CE
∠EAC=∠C
△ABC的内角和为180°
∠B+∠BAE +∠EAC+∠C=180°
90°+16°+∠EAC+∠C=180°
∠EAC=∠C=37°
分析:
例 如图,在Rt△ABC中,∠B=90°,ED是AC的垂直平分线,交AC于点D,交BC于点E.已知∠BAE=16°,那么∠C的度数是多少?
∵ ED是AC的垂直平分线
∴ AE=CE
∴ △AEC是等腰三角形
∴ ∠EAC=∠C
∵ △ABC的内角和为180°
∴ ∠B+∠BAE +∠EAC+∠C=180°
90°+16°+∠EAC+∠C=180°
∠EAC+∠C=74°
A
B
C
D
E
∵ ∠EAC=∠C
∴ ∠EAC=∠C=37°
解:
小结:本题考查了线段垂直平分线的性质,等腰三角形的性质,及三角形内角和定理.解答本题的关键是推出∠EAC=∠C.
例 如图,已知△ABC中,∠ABC=50 ,P为△ABC内一点,过点P的直线MN分别交AB,BC于点M,N.若点M在线段PA的垂直平分线上,点N在PC的垂直平分线上,则∠APC的度数是多少?
A
B
C
M
N
P
AM=PM
∠1=∠2
∠1 +∠2+∠3=180°
∠m+∠3=180°
∠m=∠1+∠2=2∠2
NP=NC
∠4=∠5
∠4+∠5+∠6=180°
∠n+∠6=180°
∠n=∠4+∠5=2∠5
分析:
∠MAP=∠1
设:
∠MPA=∠2
∠AMP=∠3
∠NCP=∠4
∠NPC=∠5
∠CNP=∠6
∠BMP=∠m
∠BNP=∠n
n
m
1
2
3
4
5
6
A
B
C
M
N
P
∠B+∠m+∠n=180°
∠B+2∠2+2∠5=180°
∠B=50
2∠2+2∠5=130°
∠2+∠5=65°
∠APC+∠2+∠5=180°
∠APC=115°
分析:
n
m
1
2
3
4
5
6
例 如图,已知△ABC中,∠ABC=50 ,P为△ABC内一点,过点P的直线MN分别交AB,BC于点M,N.若点M在线段PA的垂直平分线上,点N在PC的垂直平分线上,则∠APC的度数是多少?
A
B
C
M
N
P
n
m
1
2
3
4
5
6
∠MAP=∠1
设:
∠MPA=∠2
∠AMP=∠3
∠NCP=∠4
∠NPC=∠5
∠CNP=∠6
∠BMP=∠m
∠BNP=∠n
解:
例 如图,已知△ABC中,∠ABC=50 ,P为△ABC内一点,过点P的直线MN分别交AB,BC于点M,N.若点M在线段PA的垂直平分线上,点N在PC的垂直平分线上,则∠APC的度数是多少?
A
B
C
M
N
P
∵点M在线段PA的垂直平分线上
∴ AM=PM
∴ ∠1=∠2
∵∠1 +∠2+∠3=180°
且∠m+∠3=180°
∴ ∠m=∠1+∠2=2∠2
同理可得:∠n=∠4+∠5=2∠5
∵∠B+∠m+∠n=180°且∠B=50
∴50°+2∠2+2∠5=180°
∴∠2+∠5=65°
又∠APC+∠2+∠5=180°
∴∠APC=115°
解:
n
m
1
2
3
4
5
6
小结:
首先,借助线段垂直平分线的性质得到线段相等的关系;
其次,根据等边对等角,得到角相等的关系;
最后,根据三角形内角和定理,运算求得未知角.
例 如图,已知△ABC中,∠ABC=50 ,P为△ABC内一点,过点P的直线MN分别交AB,BC于点M,N.若点M在线段PA的垂直平分线上,点N在PC的垂直平分线上,则∠APC的度数是多少?
判断线段垂直平分线
线段垂直平分线的应用
定义:直线经过线段的中点且垂直这条线段
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上
作线段垂直平分线
利用线段垂直平分线性质定理的逆定理构造相等线段
求线段的数量关系
方法指引:
中点
垂直平分线即等腰
求角的度数
垂直
等边对等角
方法指引:
再 见
沪科版八年级上册数学
线段垂直平分线的应用
判断线段垂直平分线
判断线段垂直平分线的依据:
线段垂直平分线的定义
线段垂直平分线性质定理的逆定理
线段垂直平分线的定义
经过线段中点,并且垂直于这条线段的直线,叫做这条线段的垂直平分线
直线 l⊥AB,AC=BC
直线 l 垂直平分线段AB
A
B
C
l
中点
垂直
,又称“中垂线”.
方法归纳:若已知一条直线经过线段的中点并且垂直这条线段,则根据垂直平分线的定义,即可判断直线是线段的垂直平分线.
线段垂直平分线性质定理的逆定理
到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
A
B
C
DA=DB,EA=EB
DE垂直平分线段AB
l
D
E
方法归纳:根据此定理,若两点分别到一条线段两端点距离相等,则两点的连线即是线段的垂直平分线.
点D,E都在线段AB的垂直平分线上
分别以线段的两个端点为圆心,以大于线段的二分之一长度为半径画弧线,得到两个交点(两交点位于线段的两侧).
连接这两个交点.
用尺规作线段的垂直平分线
例 如图,四边形ADCB中,AC=AD,BC=BD,求证:AB垂直平分CD.
A
B
C
D
O
法一
△ABC≌△ABD
∠CAB=∠DAB
△AOC≌△AOD
∠COA=∠DOA=90°
OC=OD
AB垂直平分CD
分析:
线段垂直平分线的定义
AB⊥CD, AB平分CD
需证
例 如图,四边形ADCB中,AC=AD,BC=BD,求证:AB垂直平分CD.
法一
证明:
∵AC=AD,BC=BD,AB=AB
∴△ABC≌△ABD(SSS)
∴∠CAB=∠DAB
又∵AC=AD, AO=AO
∴△AOC≌△AOD(SAS)
∴∠COA=∠DOA=90°, OC=OD
∴ AB⊥CD,点O是CD的中点
∴ AB垂直平分CD
A
B
C
D
O
两次全等
根据定义证明线段的垂直平分线
(SSS)
(SAS)
例 如图,四边形ADCB中,AC=AD,BC=BD,求证:AB垂直平分CD.
A
B
C
D
O
法二:
△ABC≌△ABD
△CAD是等腰三角形
∠CAB=∠DAB
AO是∠CAD的角平分线
AO是△CAD的高线,也是CD的中线
AB垂直平分CD
分析:
线段垂直平分线的定义
AB⊥CD, AB平分CD
需证
等腰三角形三线合一
例 如图,四边形ADCB中,AC=AD,BC=BD,求证:AB垂直平分CD.
法二
∵AC=AD,BC=BD,AB=AB
∴△ABC≌△ABD(SSS)
∴∠CAB=∠DAB
∴AO是∠CAD的角平分线
∵ AC=AD
∴△CAD是等腰三角形
∴AO是△CAD的高线,也是CD的中线
∴ AB垂直平分CD
A
B
C
D
O
证明:
一次全等
等腰三角形三线合一
根据定义证明线段的垂直平分线
A
B
C
D
O
例 如图,四边形ADCB中,AC=AD,BC=BD,求证:AB垂直平分CD.
法三
与一条线段两个端点距离相等的点,
在这条线段的垂直平分线上
点A,B都在线段CD的垂直平分线上
分析:
AB垂直平分CD
A
B
C
D
O
例 如图,四边形ADCB中,AC=AD,BC=BD,求证:AB垂直平分CD.
法三
∵AC=AD
∴点A在CD的垂直平分线上
∵ BC=BD
∴点B在CD的垂直平分线上
∴点A与点B所在的直线是CD的垂直平分线
∴ AB垂直平分CD
证明:
小结:法一,法二都是从定义角度来判断线段垂直平分线,法三则是根据“到一条线段两个端点距离相等的点,在这条线段的垂直平分线上”来判断的.对比上述三个方法可发现方法三的证明更加简洁直接,因此要尝试选择最优解法提高逻辑思维能力.
例 如图,电信部门要在S区建一座信号发射塔.按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条高速公路m,n的距离也必须相等.发射塔应修建在什么位置?在图上标出它的位置.
A
B
O
S
m
n
到一条线段两个端点距离相等的点,在这条线段的垂直平分线上
到角两边距离相等的点在角的平分线上
发射塔在线段AB的垂直平分线和m与n夹角的角平分线的交点处
连接点A,点B,发射塔在线段AB的垂直平分线上
发射塔在m与n夹角的角平分线上
分析:
例 如图,电信部门要在S区建一座信号发射塔.按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条高速公路m,n的距离也必须相等.发射塔应修建在什么位置?在图上标出它的位置.
A
B
O
S
m
n
解:
连接AB
因为到一条线段两个端点距离相等的点,在这条线段的垂直平分线上,所以:
分别以线段的两个端点为圆心,以大于线段的二分之一长度为半径画圆
得到两个交点
连接这两个交点
到一条线段两个端点距离相等的点,在这条线段的垂直平分线上
例 如图,电信部门要在S区建一座信号发射塔.按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条高速公路m,n的距离也必须相等.发射塔应修建在什么位置?在图上标出它的位置.
A
B
O
S
m
n
因为到角两边距离相等的点在角的平分线上
所以:以点O为圆心,以任意长为半径画圆,分别交直线m,n于点M,N.
分别以点M,N为圆心,以大于 MN的长度为半径画圆, 两圆交于点P.
作射线OP
M
N
P
C
∠MON的角平分线与AB的垂直平分线相交于点C
发射塔应修建在点C,点C到A,B距离相等,到直线m,n的距离也相等.
解:
到角两边距离相等的点在角的平分线上
小结:熟练掌握利用尺规作角的平分线及线段的垂直平分线是解题的关键.
求线段之间的关系
添加环节P
求线段之间的关系:
求线段长或线段之间的数量关系
探究线段位置关系
直线 l 垂直平分线段AB
线段垂直平分线的性质
线段垂直平分线上的点到这条线段两个端点的距离相等.
A
B
C
l
D
DA=DB
线段垂直平分线的性质
直线 l 垂直平分线段AB
DC⊥AB,BC=AC
点C是线段AB的中点
DC是等腰△DAB的高、中线
DA=DB
△DAB是等腰三角形
A
B
C
l
D
线段的特殊位置关系
平行∥
垂直⊥
例 如图,AD⊥BC,BD=CD,点C在AE的垂直平分线上,若AB=5cm,BD=3cm.求BE的长.
A
B
C
D
E
AD垂直平分BC
AB=AC
AC=EC
AB=AC=EC=5cm
BD=CD=3cm
BE=BD+CD+EC=11cm
5cm
3cm
3cm
分析:
例 如图,AD⊥BC,BD=CD,点C在AE的垂直平分线上,若AB=5cm,BD=3cm.求BE的长.
A
B
C
D
E
5cm
3cm
3cm
∵ AD⊥BC,BD=CD
∴AD所在的直线是BC的垂直平分线
∴ AB=AC
又∵点C在AE的垂直平分线上
∴AC=EC
∴ AB=AC=EC=5cm
又BD=CD=3cm
∴BE=BD+CD+EC=11cm
解:
小结:
首先,利用垂直平分线的定义判定线段的垂直平分线;
其次,根据点在垂直平分线上,得到线段相等的关系;
最后,进行线段长度的计算.
例 如图,在D,E分别是线段AB,AC的中点,CD⊥AB,垂足为D,BE⊥AC,垂足为E.求证:AC=AB.
A
B
C
D
E
连接BC
D是线段AB的中点且CD⊥AB
AC=BC
E是线段AC的中点且BE⊥AC
AB=BC
AC=AB
分析:
CD是线段AB的垂直平分线
BE是线段AC的垂直平分线
例 如图,在D,E分别是线段AB,AC的中点,CD⊥AB,垂足为D,BE⊥AC,垂足为E.求证:AC=AB.
A
B
C
D
E
连接BC
∵ 点D是线段AB的中点且CD⊥AB
∴ AC=BC
又∵点E是线段AC的中点且BE⊥AC
∴AB=BC
∴ AC=BC=AB
∴AC=AB
证明:
小结:利用线段垂直平分线的性质得出对应线段相等,再进行等量代换是解决此题的关键.
∴ CD是线段AB的垂直平分线
∴ BE是线段AC的垂直平分线
例 如图,在△ABC中,AD是∠BAC的平分线,DE,DF分别是△ABD和△ACD的高.试猜想:AD与EF之间有什么位置关系?请证明你的猜想.
A
B
C
D
E
F
DE⊥AB,DF⊥AC
AD是公共边
Rt△ADE≌ Rt△ADF(HL)
AE=AF
AD垂直平分EF
分析:
DE=DF
AD是∠BAC的平分线
例 如图,在△ABC中,AD是∠BAC的平分线,DE,DF分别是△ABD和△ACD的高.试猜想:AD与EF之间有什么位置关系?请证明你的猜想.
∵ DE,DF分别是△ABD和△ACD的高,
∴ DE⊥AB,DF⊥AC,
∵ AD是∠BAC的平分线,
∴ DE=DF,
又∵AD是公共边,DE=DF
∴ Rt△ADE≌ Rt△ADF(HL),
A
B
C
D
E
F
∴ AE=AF,
∴ AD垂直平分EF.
猜想:AD垂直平分EF.
证明:
小结: 探究两条线段的位置关系时,先猜想垂直平分的关系,再根据已知条件来进行推理证明.
∴点A在线段EF的垂直平分线上
∴点D都在线段EF的垂直平分线上
求角的度数
求角的度数
从定义角度:垂直
从性质角度:等边对等角
求角的度数
引例
A
B
C
D
如图,AD垂直平分线段BC
则AD⊥BC,BD=CD,
则AB=AC,
∠ADB=∠ADC=90°
∠B=∠C
定义角度
性质角度
角的关系
例 如图,在Rt △ABC中,∠B=90°,ED是AC的垂直平分线,交AC于点D,交BC于点E.已知∠BAE=16°,那么∠C的度数是多少?
A
B
C
D
E
ED是AC的垂直平分线
AE=CE
∠EAC=∠C
△ABC的内角和为180°
∠B+∠BAE +∠EAC+∠C=180°
90°+16°+∠EAC+∠C=180°
∠EAC=∠C=37°
分析:
例 如图,在Rt△ABC中,∠B=90°,ED是AC的垂直平分线,交AC于点D,交BC于点E.已知∠BAE=16°,那么∠C的度数是多少?
∵ ED是AC的垂直平分线
∴ AE=CE
∴ △AEC是等腰三角形
∴ ∠EAC=∠C
∵ △ABC的内角和为180°
∴ ∠B+∠BAE +∠EAC+∠C=180°
90°+16°+∠EAC+∠C=180°
∠EAC+∠C=74°
A
B
C
D
E
∵ ∠EAC=∠C
∴ ∠EAC=∠C=37°
解:
小结:本题考查了线段垂直平分线的性质,等腰三角形的性质,及三角形内角和定理.解答本题的关键是推出∠EAC=∠C.
例 如图,已知△ABC中,∠ABC=50 ,P为△ABC内一点,过点P的直线MN分别交AB,BC于点M,N.若点M在线段PA的垂直平分线上,点N在PC的垂直平分线上,则∠APC的度数是多少?
A
B
C
M
N
P
AM=PM
∠1=∠2
∠1 +∠2+∠3=180°
∠m+∠3=180°
∠m=∠1+∠2=2∠2
NP=NC
∠4=∠5
∠4+∠5+∠6=180°
∠n+∠6=180°
∠n=∠4+∠5=2∠5
分析:
∠MAP=∠1
设:
∠MPA=∠2
∠AMP=∠3
∠NCP=∠4
∠NPC=∠5
∠CNP=∠6
∠BMP=∠m
∠BNP=∠n
n
m
1
2
3
4
5
6
A
B
C
M
N
P
∠B+∠m+∠n=180°
∠B+2∠2+2∠5=180°
∠B=50
2∠2+2∠5=130°
∠2+∠5=65°
∠APC+∠2+∠5=180°
∠APC=115°
分析:
n
m
1
2
3
4
5
6
例 如图,已知△ABC中,∠ABC=50 ,P为△ABC内一点,过点P的直线MN分别交AB,BC于点M,N.若点M在线段PA的垂直平分线上,点N在PC的垂直平分线上,则∠APC的度数是多少?
A
B
C
M
N
P
n
m
1
2
3
4
5
6
∠MAP=∠1
设:
∠MPA=∠2
∠AMP=∠3
∠NCP=∠4
∠NPC=∠5
∠CNP=∠6
∠BMP=∠m
∠BNP=∠n
解:
例 如图,已知△ABC中,∠ABC=50 ,P为△ABC内一点,过点P的直线MN分别交AB,BC于点M,N.若点M在线段PA的垂直平分线上,点N在PC的垂直平分线上,则∠APC的度数是多少?
A
B
C
M
N
P
∵点M在线段PA的垂直平分线上
∴ AM=PM
∴ ∠1=∠2
∵∠1 +∠2+∠3=180°
且∠m+∠3=180°
∴ ∠m=∠1+∠2=2∠2
同理可得:∠n=∠4+∠5=2∠5
∵∠B+∠m+∠n=180°且∠B=50
∴50°+2∠2+2∠5=180°
∴∠2+∠5=65°
又∠APC+∠2+∠5=180°
∴∠APC=115°
解:
n
m
1
2
3
4
5
6
小结:
首先,借助线段垂直平分线的性质得到线段相等的关系;
其次,根据等边对等角,得到角相等的关系;
最后,根据三角形内角和定理,运算求得未知角.
例 如图,已知△ABC中,∠ABC=50 ,P为△ABC内一点,过点P的直线MN分别交AB,BC于点M,N.若点M在线段PA的垂直平分线上,点N在PC的垂直平分线上,则∠APC的度数是多少?
判断线段垂直平分线
线段垂直平分线的应用
定义:直线经过线段的中点且垂直这条线段
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上
作线段垂直平分线
利用线段垂直平分线性质定理的逆定理构造相等线段
求线段的数量关系
方法指引:
中点
垂直平分线即等腰
求角的度数
垂直
等边对等角
方法指引:
再 见
