15.1轴对称图形-解读轴对称 课件 (共39张PPT)2023--2024学年沪科版数学八年级上册
文档属性
| 名称 | 15.1轴对称图形-解读轴对称 课件 (共39张PPT)2023--2024学年沪科版数学八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-14 00:00:00 | ||
图片预览






文档简介
(共39张PPT)
沪科版八年级上册数学
解读轴对称
轴对称与轴对称图形
认识轴对称图形与两图形成轴对称
观察下列图形有什么特征?
如果一个平面图形沿着一条直线折叠,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫做它的对称轴,这时,我们也就说这个图形关于这条直线(成轴)对称.
观察下列图形有什么特征?
认识轴对称图形与两图形成轴对称
把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么这两图形叫做关于这条直线(成轴)对称,这条直线叫做对称轴,折后重合的点是对应点,又叫做对称点.
两个图形成轴对称:
认识轴对称图形与两图形成轴对称
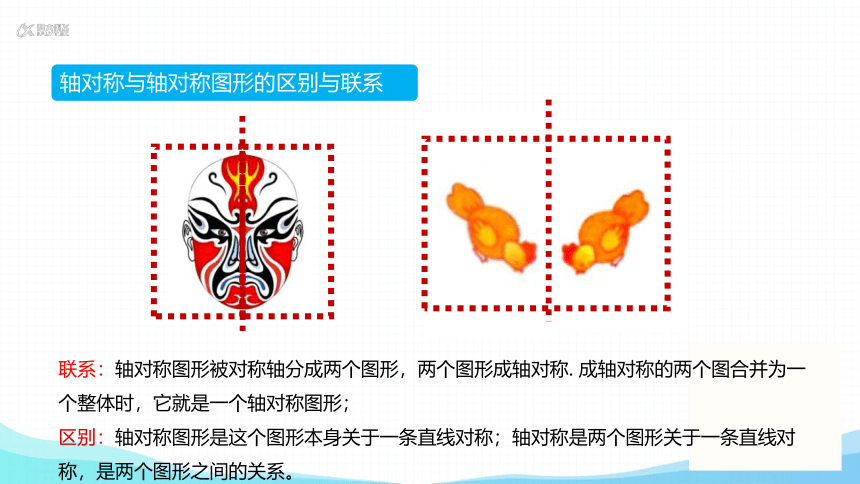
联系:轴对称图形被对称轴分成两个图形,两个图形成轴对称. 成轴对称的两个图合并为一个整体时,它就是一个轴对称图形;
区别:轴对称图形是这个图形本身关于一条直线对称;轴对称是两个图形关于一条直线对称,是两个图形之间的关系。
轴对称与轴对称图形的区别与联系
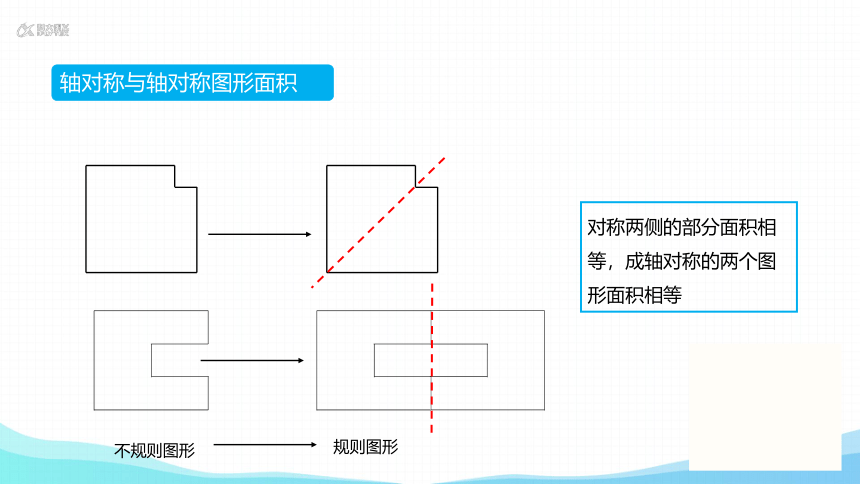
轴对称与轴对称图形面积
对称两侧的部分面积相等,成轴对称的两个图形面积相等
不规则图形
规则图形
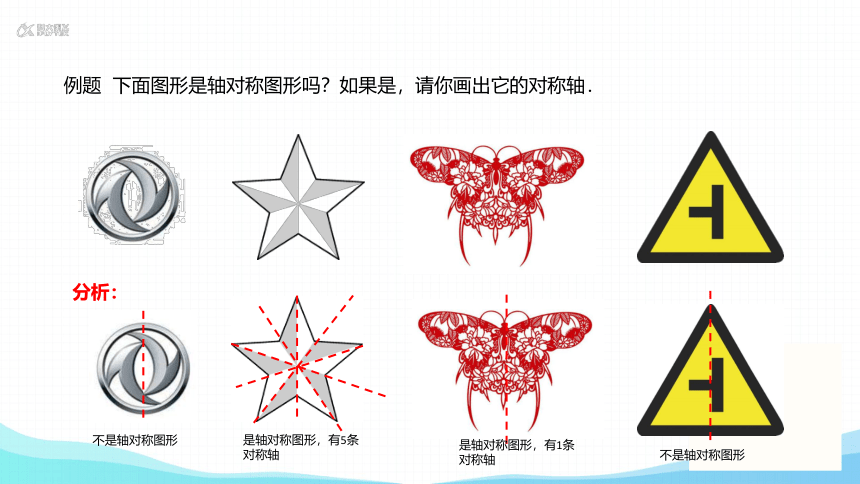
例题 下面图形是轴对称图形吗?如果是,请你画出它的对称轴.
分析:
不是轴对称图形
是轴对称图形,有5条对称轴
是轴对称图形,有1条对称轴
不是轴对称图形
例题 下面图形是轴对称图形吗?如果是,请你画出它的对称轴.
解:
第一幅图不是轴对称图形
第二幅图是轴对称图形,有5条对称轴
第三幅图是轴对称图形,有1条对称轴
第四幅图不是轴对称图形
小结:在判断轴对称图形时,一般把线段中点连线、对角线连线等作为对称轴.
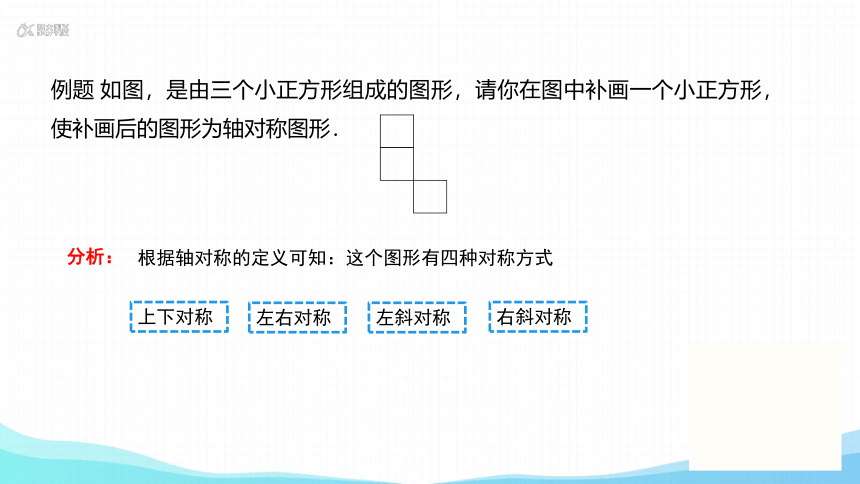
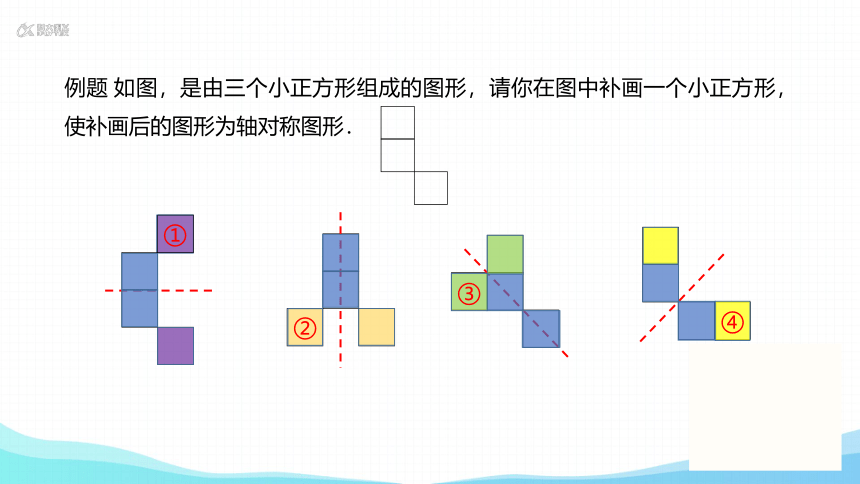
例题 如图,是由三个小正方形组成的图形,请你在图中补画一个小正方形,使补画后的图形为轴对称图形.
分析:
根据轴对称的定义可知:这个图形有四种对称方式
上下对称
左右对称
左斜对称
右斜对称
①
例题 如图,是由三个小正方形组成的图形,请你在图中补画一个小正方形,使补画后的图形为轴对称图形.
②
③
④
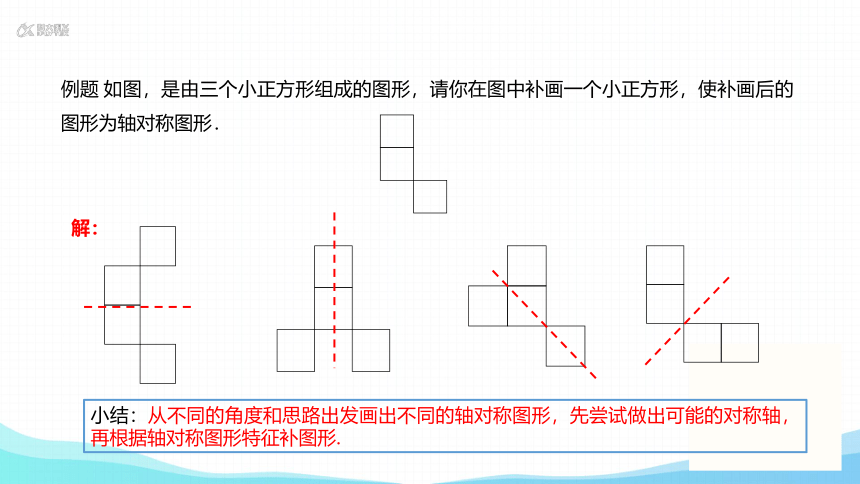
例题 如图,是由三个小正方形组成的图形,请你在图中补画一个小正方形,使补画后的图形为轴对称图形.
解:
小结:从不同的角度和思路出发画出不同的轴对称图形,先尝试做出可能的对称轴,再根据轴对称图形特征补图形.
例题 下列说法正确的是( )
A. 如果图形甲和图形乙关于直线MN对称,则图形甲是轴对称图形.
B. 任何一个图形都有对称轴,有的图形不止一条对称轴.
C. 平面上两个全等的图形一定关于某直线对称.
D. 如果ABC和EFG成轴对称,那么它们的周长一定相等.
分析:
甲和乙两个图形关于直线MN成轴对称,但是甲图形不一定是轴对称图形
注意区分轴对称图形和两个图形成轴对称的概念
乙
甲
M
N
例题 下列说法正确的是( )
A. 如果图形甲和图形乙关于直线MN对称,则图形甲是轴对称图形.
B. 任何一个图形都有对称轴,有的图形不止一条对称轴.
C. 平面上两个全等的图形一定关于某直线对称.
D. 如果ABC和EFG成轴对称,那么它们的周长一定相等.
分析:
不是任何一个图形都有对称轴,只有轴对称图形才有
例题 下列说法正确的是( )
A. 如果图形甲和图形乙关于直线MN对称,则图形甲是轴对称图形.
B. 任何一个图形都有对称轴,有的图形不止一条对称轴.
C. 平面上两个全等的图形一定关于某直线对称.
D. 如果ABC和EFG成轴对称,那么它们的周长一定相等.
分析:
成轴对称的两个图形是全等形,但是全等图形不一定是成轴对称图形
注意成轴对称图形的性质
例题 下列说法正确的是( )
A. 如果图形甲和图形乙关于直线MN对称,则图形甲是轴对称图形.
B. 任何一个图形都有对称轴,有的图形不止一条对称轴.
C. 平面上两个全等的图形一定关于某直线对称.
D. 如果ABC和EFG成轴对称,那么它们的周长一定相等.
分析:
如果ABC和EFG成轴对称,那么它们的周长一定相等.
考查轴对称性质,对应边相等,对应角相等,所以周长相等
D
小结:理解轴对称的定义及性质,区别轴对称及两个图形成轴对称的概念,是解决本题的关键.
例 △ABC为等腰三角形, AB=AC,点D为底边BC的中点,若BC=11cm,AD=12cm,求阴影面积.
分析:
△ABC为等腰三角形, AB=AC,D为底边BC的中点
△EBF≌△ECF
△EBF和△ECF关于AD所在的直线成轴对称
阴影面积=ABD的面积
A
B
D
C
解:
∵ ABC为等腰三角形,点D为底边BC的中点
∴ AD⊥BC,AD为△ABC 的对称轴
∴ △EBF和△ECF关于AD所在的直线成轴对称
∵ BC=11cm, AD=12cm
即阴影部分面积为33 cm2
∴ S阴=S△ABD=
小结:通过观察图形特征,发现△EBF和△ECF关于AD所在的直线成轴对称,这两个三角形的面积相等是解题的关键.
11cm
12cm
E
F
例 △ABC为等腰三角形, AB=AC,点D为底边BC的中点,若BC=11cm,AD=12cm,求阴影面积.
∴S△EBF =S△ECF
轴对称的应用
坐标思想
图形变换
轴对称的应用
在平面坐标系中作轴对称图形
已知点 (x,y)
关于x轴的对称点 (x,-y)
关于y轴的对称点 (-x,y)
(x,y)
(x,-y)
(-x,y)
坐标思想
图形变换
两点之间线段最短,三角形三边关系
轴对称的应用
在平面坐标系中作轴对称图形
作最短路径
A
B
C
C’
A
B
C’
B’
C
分析:
例题 如图,在网格中作出ABC关于x轴和y轴对称的图形,并求出各对应点的坐标.
B (2,4)
A (0,2)
C (3,-2)
作关于x轴的对称图形,先作点的对称然后连线
A(0,2)关于x轴的对称点为A1(0,-2)
A1(0,-2)
B(2,4)关于x轴的对称点为B1(2,-4)
C(3,-2)关于x轴的对称点为C1(3,2)
B1(2,-4)
C1(3,2)
分析:
例题 如图,在网格中作出ABC关于x轴和y轴对称的图形,并求出各对应点的坐标.
B (2,4)
A (0,2)
C (3,-2)
A1(0,-2)
B1(2,-4)
C1(3,2)
已知点 A(0,2) B(2,4) C(3,-2)
关于x轴的对称点 A1(0,-2) B1(2,-4) C1(3,2)
分析:
例题 如图,在网格中作出ABC关于x轴和y轴对称的图形,并求出各对应点的坐标.
B (2,4)
A (0,2)
C (3,-2)
B2(-2,4)
C2(-3,-2)
A2
已知点 A(0,2) B(2,4) C(3,-2)
关于y轴的对称点 A2(0,2) B2(-2,4) C2(-3,-2)
解:
例题 如图,在网格中作出ABC关于x轴和y轴对称的图形,并求出各对应点的坐标.
B (2,4)
A (0,2)
C (3,-2)
小结:
根据点(x,y)关于x轴对称的点的坐标为(x,-y);点(x,y)关于y轴对称的点的坐标为(-x,y)求出点坐标,标在图上.也可根据对称轴为对称图形对应点连线的中垂线来直接作图.
已知点 A(0,2) B(2,4) C(3,-2)
关于x轴的对称点 (0,-2) (2,-4) (3,2)
关于y轴的对称点 (0,2) (-2,4) (-3,-2)
A.5个 B.6个 C.7个 D.8个
B
A
C
B
A
C
B
A
C
分析:上下对称轴
例题 如图,在3×3的网格中,与△ABC成轴对称,顶点在格点上,且位置不同的三角形有( ).
B
A
C
B
A
C
A.5个 B.6个 C.7个 D.8个
例题 如图,在3×3的网格中,与△ABC成轴对称,顶点在格点上,且位置不同的三角形有( ).
分析:左右对称轴
例题 如图,在3×3的网格中,与△ABC成轴对称,顶点在格点上,且位置不同的三角形有( ).
B
A
C
B
A
C
A.5个 B.6个 C.7个 D.8个
分析:左斜对称轴
例题 如图,在3×3的网格中,与△ABC成轴对称,顶点在格点上,且位置不同的三角形有( ).
B
A
C
A.5个 B.6个 C.7个 D.8个
分析:右斜对称轴
例题 如图,在3×3的网格中,与△ABC成轴对称,顶点在格点上,且位置不同的三角形有( ).
B
A
C
B
A
C
B
A
C
B
A
C
B
A
C
B
A
C
B
A
C
B
A
C
分析:
D
A.5个 B.6个 C.7个 D.8个
小结:
观察图形,根据图形特点先确定对称轴,图形往往呈上下对称,对称轴为横线;左右对称,对称轴为竖线;左斜对称,右斜对称,对称轴为45°方向的斜线. 确定对称轴后,再补全对称图形.
B
A
C
例题 如图,在3×3的网格中,与△ABC成轴对称,顶点在格点上,且位置不同的三角形有( ).
A.5个 B.6个 C.7个 D.8个
D
例题 如图, 等腰三角形ABC的底边BC长为4,面积是12,腰AB的垂直平分线EF分别交AB、AC于点E、F,若点D为底边BC的中点,点M为线段EF上一动点,求BDM的周长的最小值.
A
B
C
D
E
F
M
分析:
要求BDM的周长最小值
求BD+DM+BM最小值
求DM+BM最小值
由EF是AB的垂直平分线,连接AM,则AM=BM
由BC=4,D为BC中点,可知BD=2
求DM+AM最小值
AD的长就是DM+AM的最小值,即DM+BM的最小值
连AD交EF与点M ,
M ,
BDM的周长最小值就是BD+AD
A
B
C
D
E
F
M
解:
连接AD交EF与点M ,
M ,
∵△ABC是等腰三角形,点D是BC的中点且BC=4
∴AD⊥BC,BD=2
又∵△ABC面积是12
例题 如图, 等腰三角形ABC的底边BC长为4,面积是12,腰AB的垂直平分线EF分别交AB、AC于点E、F,若点D为底边BC的中点,点M为线段EF上一动点,求BDM的周长的最小值.
∴AD=6
∴
6
2
A
B
C
D
E
F
M
∵EF是线段AB的垂直平分线
∴BM=AM
∴BM+MD=AM+MD
∴当点M位于点M ,处时,BM+MD有最小值,最小值为AD的长
∴BDM的周长最小值为BD+AD=2+6=8
∵AM+MD ≥ AD
例题 如图, 等腰三角形ABC的底边BC长为4,面积是12,腰AB的垂直平分线EF分别交AB、AC于点E、F,若点D为底边BC的中点,点M为线段EF上一动点,求BDM的周长的最小值.
连接AM
小结:本题考查轴对称最短路径问题,熟知等腰三角形三线合一的性质是解题的关键.
M ,
6
2
解:
例题 如图,∠AOB=30°,点M,N分别是射线OA,OB上的动点,OP平分∠AOB,且OP=6,求PMN的周长最小值.
A
O
B
P
M
N
分析:
要求 PMN 的周长最小值
求PM+MN+PN的最小值
C
D
作点P关于射线OA,OB的对称点C,D,连CM,DN
M ,
N ,
求CM+MN+DN的最小值
连CD,交OA,OB于点M ,,N ,
当C, M ,N ,D四点共线即M,N 分别与M ,,N ,重合时,则CD的长就是 PMN 的周长最小值
例题 如图,∠AOB=30°,点M,N分别是射线OA,OB上的动点,OP平分∠AOB,且OP=6,求PMN的周长最小值.
A
O
B
P
M
N
解:
C
D
M ,
N ,
作点P关于射线OA的对称点C,关于射线OB的对称点D
连接CM,DN,OC,OD,连接CD,交OA,OB于点M ,,N ,
CM=PM,PN=DN,
由轴对称的性质可知:
∠POB=∠DOB,
∠COA=∠POA
∵OP=6
∴OC=OP=OD=6
∵∠COD=∠COA+∠POA+∠DOB+∠POB=30°+ 30°=60°
∴COD是等边三角形
∴CD=OC=OD=6
∴ C△PMN=PM+PN+MN= CM+DN+MN
当C、M、N、D四点共线即M,N 分别与M ,,N ,重合时,
PMN周长最小,最小值为CD的长
∴ PMN周长最小值为6.
6
6
6
小结:
将“同侧”难于解决的问题转化为“异侧”容易解决的问题. 用化曲为直思想把动线段变换到动点轨迹的两侧,从而把三条动线段PM、MN、PN转化为连接两点之间的路径.
解读轴对称
轴对称与轴对称图形
轴对称的应用
认识轴对称图形与两图形成轴对称
轴对称与轴对称图形的区别与联系
对称两侧的部分面积相等,成轴对称的两个图形面积相等
在平面坐标系中作轴对称图形
作最短路径
两点之间线段最短,三角形三边关系
坐标思想
图形变换
再 见
沪科版八年级上册数学
解读轴对称
轴对称与轴对称图形
认识轴对称图形与两图形成轴对称
观察下列图形有什么特征?
如果一个平面图形沿着一条直线折叠,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫做它的对称轴,这时,我们也就说这个图形关于这条直线(成轴)对称.
观察下列图形有什么特征?
认识轴对称图形与两图形成轴对称
把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么这两图形叫做关于这条直线(成轴)对称,这条直线叫做对称轴,折后重合的点是对应点,又叫做对称点.
两个图形成轴对称:
认识轴对称图形与两图形成轴对称
联系:轴对称图形被对称轴分成两个图形,两个图形成轴对称. 成轴对称的两个图合并为一个整体时,它就是一个轴对称图形;
区别:轴对称图形是这个图形本身关于一条直线对称;轴对称是两个图形关于一条直线对称,是两个图形之间的关系。
轴对称与轴对称图形的区别与联系
轴对称与轴对称图形面积
对称两侧的部分面积相等,成轴对称的两个图形面积相等
不规则图形
规则图形
例题 下面图形是轴对称图形吗?如果是,请你画出它的对称轴.
分析:
不是轴对称图形
是轴对称图形,有5条对称轴
是轴对称图形,有1条对称轴
不是轴对称图形
例题 下面图形是轴对称图形吗?如果是,请你画出它的对称轴.
解:
第一幅图不是轴对称图形
第二幅图是轴对称图形,有5条对称轴
第三幅图是轴对称图形,有1条对称轴
第四幅图不是轴对称图形
小结:在判断轴对称图形时,一般把线段中点连线、对角线连线等作为对称轴.
例题 如图,是由三个小正方形组成的图形,请你在图中补画一个小正方形,使补画后的图形为轴对称图形.
分析:
根据轴对称的定义可知:这个图形有四种对称方式
上下对称
左右对称
左斜对称
右斜对称
①
例题 如图,是由三个小正方形组成的图形,请你在图中补画一个小正方形,使补画后的图形为轴对称图形.
②
③
④
例题 如图,是由三个小正方形组成的图形,请你在图中补画一个小正方形,使补画后的图形为轴对称图形.
解:
小结:从不同的角度和思路出发画出不同的轴对称图形,先尝试做出可能的对称轴,再根据轴对称图形特征补图形.
例题 下列说法正确的是( )
A. 如果图形甲和图形乙关于直线MN对称,则图形甲是轴对称图形.
B. 任何一个图形都有对称轴,有的图形不止一条对称轴.
C. 平面上两个全等的图形一定关于某直线对称.
D. 如果ABC和EFG成轴对称,那么它们的周长一定相等.
分析:
甲和乙两个图形关于直线MN成轴对称,但是甲图形不一定是轴对称图形
注意区分轴对称图形和两个图形成轴对称的概念
乙
甲
M
N
例题 下列说法正确的是( )
A. 如果图形甲和图形乙关于直线MN对称,则图形甲是轴对称图形.
B. 任何一个图形都有对称轴,有的图形不止一条对称轴.
C. 平面上两个全等的图形一定关于某直线对称.
D. 如果ABC和EFG成轴对称,那么它们的周长一定相等.
分析:
不是任何一个图形都有对称轴,只有轴对称图形才有
例题 下列说法正确的是( )
A. 如果图形甲和图形乙关于直线MN对称,则图形甲是轴对称图形.
B. 任何一个图形都有对称轴,有的图形不止一条对称轴.
C. 平面上两个全等的图形一定关于某直线对称.
D. 如果ABC和EFG成轴对称,那么它们的周长一定相等.
分析:
成轴对称的两个图形是全等形,但是全等图形不一定是成轴对称图形
注意成轴对称图形的性质
例题 下列说法正确的是( )
A. 如果图形甲和图形乙关于直线MN对称,则图形甲是轴对称图形.
B. 任何一个图形都有对称轴,有的图形不止一条对称轴.
C. 平面上两个全等的图形一定关于某直线对称.
D. 如果ABC和EFG成轴对称,那么它们的周长一定相等.
分析:
如果ABC和EFG成轴对称,那么它们的周长一定相等.
考查轴对称性质,对应边相等,对应角相等,所以周长相等
D
小结:理解轴对称的定义及性质,区别轴对称及两个图形成轴对称的概念,是解决本题的关键.
例 △ABC为等腰三角形, AB=AC,点D为底边BC的中点,若BC=11cm,AD=12cm,求阴影面积.
分析:
△ABC为等腰三角形, AB=AC,D为底边BC的中点
△EBF≌△ECF
△EBF和△ECF关于AD所在的直线成轴对称
阴影面积=ABD的面积
A
B
D
C
解:
∵ ABC为等腰三角形,点D为底边BC的中点
∴ AD⊥BC,AD为△ABC 的对称轴
∴ △EBF和△ECF关于AD所在的直线成轴对称
∵ BC=11cm, AD=12cm
即阴影部分面积为33 cm2
∴ S阴=S△ABD=
小结:通过观察图形特征,发现△EBF和△ECF关于AD所在的直线成轴对称,这两个三角形的面积相等是解题的关键.
11cm
12cm
E
F
例 △ABC为等腰三角形, AB=AC,点D为底边BC的中点,若BC=11cm,AD=12cm,求阴影面积.
∴S△EBF =S△ECF
轴对称的应用
坐标思想
图形变换
轴对称的应用
在平面坐标系中作轴对称图形
已知点 (x,y)
关于x轴的对称点 (x,-y)
关于y轴的对称点 (-x,y)
(x,y)
(x,-y)
(-x,y)
坐标思想
图形变换
两点之间线段最短,三角形三边关系
轴对称的应用
在平面坐标系中作轴对称图形
作最短路径
A
B
C
C’
A
B
C’
B’
C
分析:
例题 如图,在网格中作出ABC关于x轴和y轴对称的图形,并求出各对应点的坐标.
B (2,4)
A (0,2)
C (3,-2)
作关于x轴的对称图形,先作点的对称然后连线
A(0,2)关于x轴的对称点为A1(0,-2)
A1(0,-2)
B(2,4)关于x轴的对称点为B1(2,-4)
C(3,-2)关于x轴的对称点为C1(3,2)
B1(2,-4)
C1(3,2)
分析:
例题 如图,在网格中作出ABC关于x轴和y轴对称的图形,并求出各对应点的坐标.
B (2,4)
A (0,2)
C (3,-2)
A1(0,-2)
B1(2,-4)
C1(3,2)
已知点 A(0,2) B(2,4) C(3,-2)
关于x轴的对称点 A1(0,-2) B1(2,-4) C1(3,2)
分析:
例题 如图,在网格中作出ABC关于x轴和y轴对称的图形,并求出各对应点的坐标.
B (2,4)
A (0,2)
C (3,-2)
B2(-2,4)
C2(-3,-2)
A2
已知点 A(0,2) B(2,4) C(3,-2)
关于y轴的对称点 A2(0,2) B2(-2,4) C2(-3,-2)
解:
例题 如图,在网格中作出ABC关于x轴和y轴对称的图形,并求出各对应点的坐标.
B (2,4)
A (0,2)
C (3,-2)
小结:
根据点(x,y)关于x轴对称的点的坐标为(x,-y);点(x,y)关于y轴对称的点的坐标为(-x,y)求出点坐标,标在图上.也可根据对称轴为对称图形对应点连线的中垂线来直接作图.
已知点 A(0,2) B(2,4) C(3,-2)
关于x轴的对称点 (0,-2) (2,-4) (3,2)
关于y轴的对称点 (0,2) (-2,4) (-3,-2)
A.5个 B.6个 C.7个 D.8个
B
A
C
B
A
C
B
A
C
分析:上下对称轴
例题 如图,在3×3的网格中,与△ABC成轴对称,顶点在格点上,且位置不同的三角形有( ).
B
A
C
B
A
C
A.5个 B.6个 C.7个 D.8个
例题 如图,在3×3的网格中,与△ABC成轴对称,顶点在格点上,且位置不同的三角形有( ).
分析:左右对称轴
例题 如图,在3×3的网格中,与△ABC成轴对称,顶点在格点上,且位置不同的三角形有( ).
B
A
C
B
A
C
A.5个 B.6个 C.7个 D.8个
分析:左斜对称轴
例题 如图,在3×3的网格中,与△ABC成轴对称,顶点在格点上,且位置不同的三角形有( ).
B
A
C
A.5个 B.6个 C.7个 D.8个
分析:右斜对称轴
例题 如图,在3×3的网格中,与△ABC成轴对称,顶点在格点上,且位置不同的三角形有( ).
B
A
C
B
A
C
B
A
C
B
A
C
B
A
C
B
A
C
B
A
C
B
A
C
分析:
D
A.5个 B.6个 C.7个 D.8个
小结:
观察图形,根据图形特点先确定对称轴,图形往往呈上下对称,对称轴为横线;左右对称,对称轴为竖线;左斜对称,右斜对称,对称轴为45°方向的斜线. 确定对称轴后,再补全对称图形.
B
A
C
例题 如图,在3×3的网格中,与△ABC成轴对称,顶点在格点上,且位置不同的三角形有( ).
A.5个 B.6个 C.7个 D.8个
D
例题 如图, 等腰三角形ABC的底边BC长为4,面积是12,腰AB的垂直平分线EF分别交AB、AC于点E、F,若点D为底边BC的中点,点M为线段EF上一动点,求BDM的周长的最小值.
A
B
C
D
E
F
M
分析:
要求BDM的周长最小值
求BD+DM+BM最小值
求DM+BM最小值
由EF是AB的垂直平分线,连接AM,则AM=BM
由BC=4,D为BC中点,可知BD=2
求DM+AM最小值
AD的长就是DM+AM的最小值,即DM+BM的最小值
连AD交EF与点M ,
M ,
BDM的周长最小值就是BD+AD
A
B
C
D
E
F
M
解:
连接AD交EF与点M ,
M ,
∵△ABC是等腰三角形,点D是BC的中点且BC=4
∴AD⊥BC,BD=2
又∵△ABC面积是12
例题 如图, 等腰三角形ABC的底边BC长为4,面积是12,腰AB的垂直平分线EF分别交AB、AC于点E、F,若点D为底边BC的中点,点M为线段EF上一动点,求BDM的周长的最小值.
∴AD=6
∴
6
2
A
B
C
D
E
F
M
∵EF是线段AB的垂直平分线
∴BM=AM
∴BM+MD=AM+MD
∴当点M位于点M ,处时,BM+MD有最小值,最小值为AD的长
∴BDM的周长最小值为BD+AD=2+6=8
∵AM+MD ≥ AD
例题 如图, 等腰三角形ABC的底边BC长为4,面积是12,腰AB的垂直平分线EF分别交AB、AC于点E、F,若点D为底边BC的中点,点M为线段EF上一动点,求BDM的周长的最小值.
连接AM
小结:本题考查轴对称最短路径问题,熟知等腰三角形三线合一的性质是解题的关键.
M ,
6
2
解:
例题 如图,∠AOB=30°,点M,N分别是射线OA,OB上的动点,OP平分∠AOB,且OP=6,求PMN的周长最小值.
A
O
B
P
M
N
分析:
要求 PMN 的周长最小值
求PM+MN+PN的最小值
C
D
作点P关于射线OA,OB的对称点C,D,连CM,DN
M ,
N ,
求CM+MN+DN的最小值
连CD,交OA,OB于点M ,,N ,
当C, M ,N ,D四点共线即M,N 分别与M ,,N ,重合时,则CD的长就是 PMN 的周长最小值
例题 如图,∠AOB=30°,点M,N分别是射线OA,OB上的动点,OP平分∠AOB,且OP=6,求PMN的周长最小值.
A
O
B
P
M
N
解:
C
D
M ,
N ,
作点P关于射线OA的对称点C,关于射线OB的对称点D
连接CM,DN,OC,OD,连接CD,交OA,OB于点M ,,N ,
CM=PM,PN=DN,
由轴对称的性质可知:
∠POB=∠DOB,
∠COA=∠POA
∵OP=6
∴OC=OP=OD=6
∵∠COD=∠COA+∠POA+∠DOB+∠POB=30°+ 30°=60°
∴COD是等边三角形
∴CD=OC=OD=6
∴ C△PMN=PM+PN+MN= CM+DN+MN
当C、M、N、D四点共线即M,N 分别与M ,,N ,重合时,
PMN周长最小,最小值为CD的长
∴ PMN周长最小值为6.
6
6
6
小结:
将“同侧”难于解决的问题转化为“异侧”容易解决的问题. 用化曲为直思想把动线段变换到动点轨迹的两侧,从而把三条动线段PM、MN、PN转化为连接两点之间的路径.
解读轴对称
轴对称与轴对称图形
轴对称的应用
认识轴对称图形与两图形成轴对称
轴对称与轴对称图形的区别与联系
对称两侧的部分面积相等,成轴对称的两个图形面积相等
在平面坐标系中作轴对称图形
作最短路径
两点之间线段最短,三角形三边关系
坐标思想
图形变换
再 见
