北师大版数学八年级上册3.2平面直角坐标系第3课时 建立适当的坐标系描述图形的位置 导学案(含答案)
文档属性
| 名称 | 北师大版数学八年级上册3.2平面直角坐标系第3课时 建立适当的坐标系描述图形的位置 导学案(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 182.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-15 00:00:00 | ||
图片预览


文档简介
第三章 位置与坐标
2 平面直角坐标系
第3课时 建立适当的坐标系描述图形的位置
学习目标
1.能结合所给图形的特点,建立适当的坐标系,写出点的坐标.
2.能根据一些特殊点的坐标复原坐标系.
3.经历建立坐标系描述图形的过程,进一步发展数形结合意识.
学习策略
1.根据实际问题建立适当的坐标系,并能写出各点的坐标.
2.根据一些特殊点的坐标复原坐标系.
学习过程
一情境导入:
复习:(1)如何建立平面直角坐标系 说一说各个象限内点的坐标特征.
(2)如图(1)所示,求出A,B,C,D,E,F的坐标.
(3)在直角坐标系中,设法找到若干个点使得连接各点所得的封闭图形是如图(2)所示的“十”字.
二.新课学习:
如图所示,长方形ABCD的长与宽分别是6,4,建立适当的直角坐标系,并写出各个顶点的坐标.
思考:在没有直角坐标系的情况下不能写出各个顶点的坐标,所以应先建立直角坐标系,那么应如何选取直角坐标系呢 请大家思考.
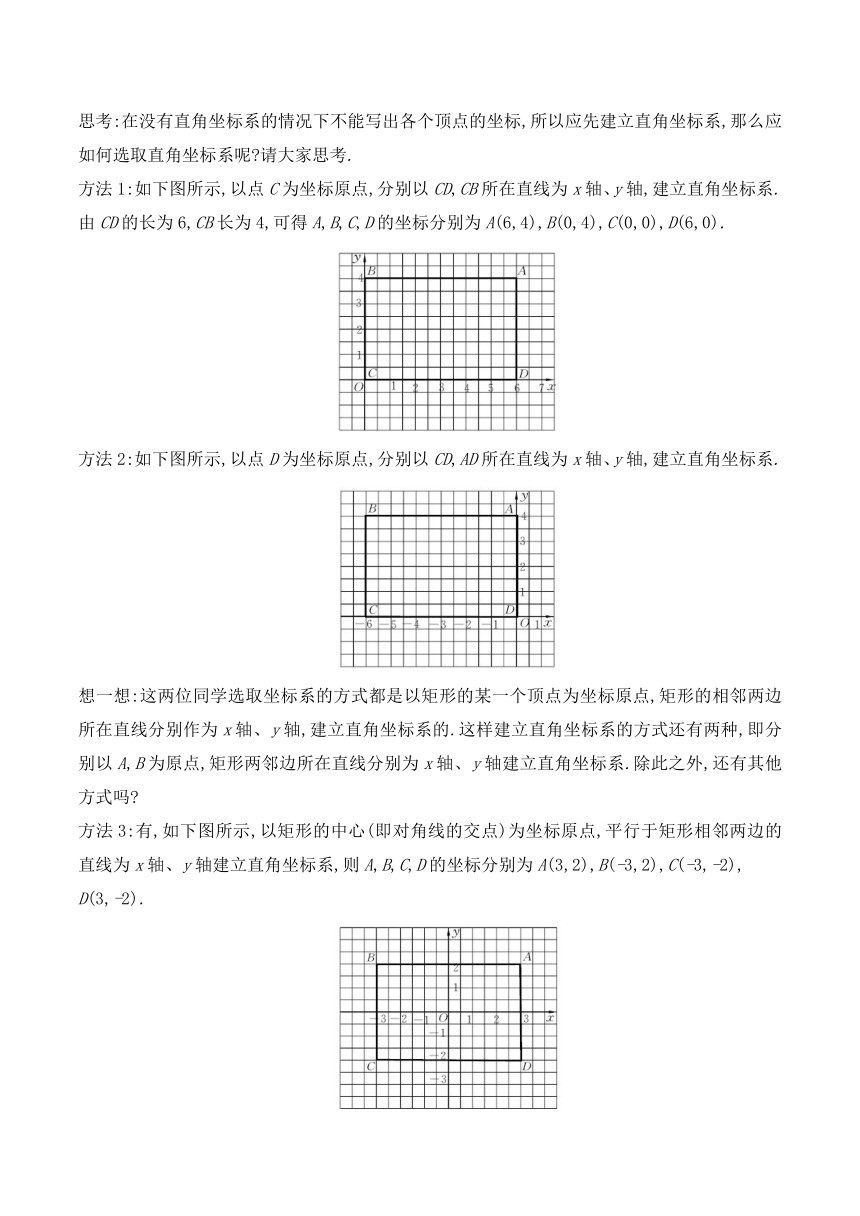
方法1:如下图所示,以点C为坐标原点,分别以CD,CB所在直线为x轴、y轴,建立直角坐标系.
由CD的长为6,CB长为4,可得A,B,C,D的坐标分别为A(6,4),B(0,4),C(0,0),D(6,0).
方法2:如下图所示,以点D为坐标原点,分别以CD,AD所在直线为x轴、y轴,建立直角坐标系.
想一想:这两位同学选取坐标系的方式都是以矩形的某一个顶点为坐标原点,矩形的相邻两边所在直线分别作为x轴、y轴,建立直角坐标系的.这样建立直角坐标系的方式还有两种,即分别以A,B为原点,矩形两邻边所在直线分别为x轴、y轴建立直角坐标系.除此之外,还有其他方式吗
方法3:有,如下图所示,以矩形的中心(即对角线的交点)为坐标原点,平行于矩形相邻两边的直线为x轴、y轴建立直角坐标系,则A,B,C,D的坐标分别为A(3,2),B(-3,2),C(-3,-2),
D(3,-2).
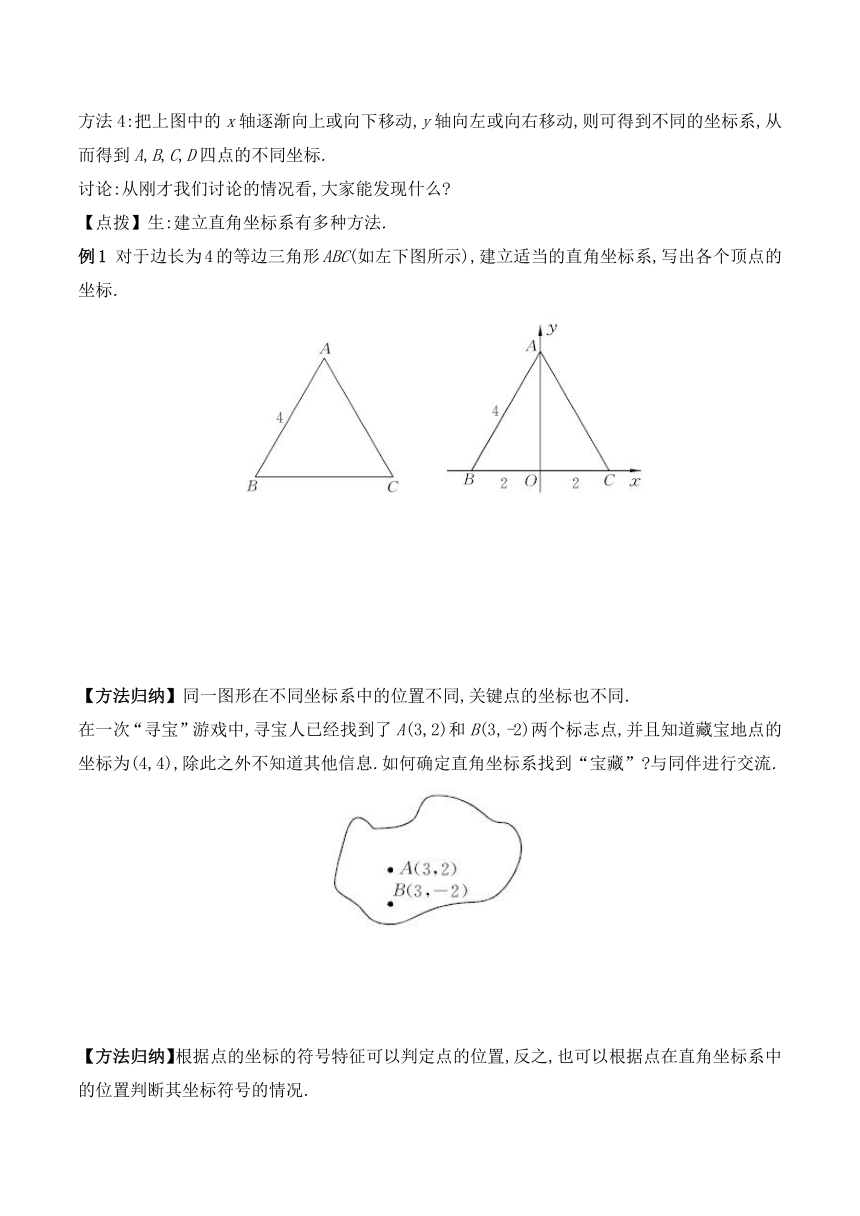
方法4:把上图中的x轴逐渐向上或向下移动,y轴向左或向右移动,则可得到不同的坐标系,从而得到A,B,C,D四点的不同坐标.
讨论:从刚才我们讨论的情况看,大家能发现什么
【点拨】生:建立直角坐标系有多种方法.
例1 对于边长为4的等边三角形ABC(如左下图所示),建立适当的直角坐标系,写出各个顶点的坐标.
【方法归纳】同一图形在不同坐标系中的位置不同,关键点的坐标也不同.
在一次“寻宝”游戏中,寻宝人已经找到了A(3,2)和B(3,-2)两个标志点,并且知道藏宝地点的坐标为(4,4),除此之外不知道其他信息.如何确定直角坐标系找到“宝藏” 与同伴进行交流.
【方法归纳】根据点的坐标的符号特征可以判定点的位置,反之,也可以根据点在直角坐标系中的位置判断其坐标符号的情况.
三.尝试应用:
1.某地为了发展城市群,在现有的四个中小城市A,B,C,D附近新建机场E,试建立适当的直角坐标系,并写出各点的坐标.
2.正方形的边长为2,建立合适的直角坐标系,写出各顶点的坐标 .
四.自主总结:
本节通过学习建立直角坐标系的多种方法,体验数学活动充满着探索与创造,不同的坐标系,对于同一个图形,点的坐标是不同的.
建立不同的平面直角坐标系,同一个图形,同一个点可以用不同的坐标表示,在实际应用中,以坐标简单容易计算为前提.
五.达标测试
1.如图所示的是A,B,C,D四位同学的家所在位置,若以A同学家的位置为坐标原点建立平面直角坐标系,那么C同学家的位置的坐标为(1,5),则B,D两同学家的坐标分别为 ( )
A.(2,3),(3,2) B.(3,2),(2,3) C.(2,3),(-3,2) D.(3,2),(-2,3)
2.如图所示,若“帅”位于点(1,-2)上,“相”位于点(3,-2)上,则“炮”位于点 .
3.如图所示,若点E的坐标为(-2,1),点F的坐标为(1,-1),则点G的坐标为 .
4.星期天,小王、小李、小张三位同学相约到文化广场游玩,出发前,他们每人带了一张利用平面直角坐标系画的示意图(如图所示),其中行政办公楼的坐标是(-4,3),南城百货的坐标是(2,-3).
(1)图中省略了平面直角坐标系,请根据上述信息,画出这个平面直角坐标系;
(2)写出图中体育馆、升旗台、北部湾俱乐部、盘龙苑小区、国际大酒店的坐标;
(3)小王、小张两人到了升旗台附近,这时还没看到小李,于是打电话问小李的位置,小李说他现在位置的坐标是(-2,-2),请在图中用字母A标出小李的位置.
5.在平面直角坐标系中,点A的坐标(-3,4),点B的坐标是(-1,-2),点O为坐标原点,求ΔAOB的面积.
如图所示,正方形ABCD的边长为10,连接各边的中点E,F,G,H得到正方形EFGH,请你建立适当的坐标系,分别写出A,B,C,D,E,F,G,H的坐标.
例题答案
例 解:如图所示,以边BC所在的直线为x轴,以边BC的中垂线为y轴建立直角坐标系.
由等边三角形的性质可知AO=2,等边三角形ABC各个顶点A,B,C的坐标分别为A(0,2),B(-2,0),C(2,0).
三.尝试应用答案
1.解:答案不唯一,可以以点A为坐标原点,建立平面直角坐标系.
2.解:答案不唯一,如图(1)所示,A(0,2),B(2,2),C(2,0),O(0,0);
如图(2)所示,A(-1,1),B(1,1),C(1,-1),D(-1,-1);
如图(3)所示,A(-2,2),B(0,2),D(-2,0),O(0,0);
如图(4)所示,A(-,0),B(0,),C(,0),D(0,-).
达标测试答案
1.D(解析:建立正确的平面直角坐标系,然后确定B,D两家的坐标.)
2.(-2,1)(解析:由“帅”位于点(1,-2),“相”位于点(3,-2),确定平面直角坐标系,再找到“炮”的位置,写出它的坐标.)
3.(1,2)
4.解:(1)建立平面直角坐标系如图所示. (2)体育馆(-9,4),升旗台(-4,2),北部湾俱乐部(-7,-1),盘龙苑小区(-5,-3),国际大酒店(0,0).
(3)小李的位置是如图所示的A点.
5.解:ΔAOB的面积是5.
6.解:答案不唯一,如:以EG所在直线为x轴,以FH所在直线为y轴,建立如图所示的坐标系,则A(-5,-5),B(5,-5),C(5,5),D(-5,5),E(-5,0),F(0,-5),G(5,0),H(0,5).
2 平面直角坐标系
第3课时 建立适当的坐标系描述图形的位置
学习目标
1.能结合所给图形的特点,建立适当的坐标系,写出点的坐标.
2.能根据一些特殊点的坐标复原坐标系.
3.经历建立坐标系描述图形的过程,进一步发展数形结合意识.
学习策略
1.根据实际问题建立适当的坐标系,并能写出各点的坐标.
2.根据一些特殊点的坐标复原坐标系.
学习过程
一情境导入:
复习:(1)如何建立平面直角坐标系 说一说各个象限内点的坐标特征.
(2)如图(1)所示,求出A,B,C,D,E,F的坐标.
(3)在直角坐标系中,设法找到若干个点使得连接各点所得的封闭图形是如图(2)所示的“十”字.
二.新课学习:
如图所示,长方形ABCD的长与宽分别是6,4,建立适当的直角坐标系,并写出各个顶点的坐标.
思考:在没有直角坐标系的情况下不能写出各个顶点的坐标,所以应先建立直角坐标系,那么应如何选取直角坐标系呢 请大家思考.
方法1:如下图所示,以点C为坐标原点,分别以CD,CB所在直线为x轴、y轴,建立直角坐标系.
由CD的长为6,CB长为4,可得A,B,C,D的坐标分别为A(6,4),B(0,4),C(0,0),D(6,0).
方法2:如下图所示,以点D为坐标原点,分别以CD,AD所在直线为x轴、y轴,建立直角坐标系.
想一想:这两位同学选取坐标系的方式都是以矩形的某一个顶点为坐标原点,矩形的相邻两边所在直线分别作为x轴、y轴,建立直角坐标系的.这样建立直角坐标系的方式还有两种,即分别以A,B为原点,矩形两邻边所在直线分别为x轴、y轴建立直角坐标系.除此之外,还有其他方式吗
方法3:有,如下图所示,以矩形的中心(即对角线的交点)为坐标原点,平行于矩形相邻两边的直线为x轴、y轴建立直角坐标系,则A,B,C,D的坐标分别为A(3,2),B(-3,2),C(-3,-2),
D(3,-2).
方法4:把上图中的x轴逐渐向上或向下移动,y轴向左或向右移动,则可得到不同的坐标系,从而得到A,B,C,D四点的不同坐标.
讨论:从刚才我们讨论的情况看,大家能发现什么
【点拨】生:建立直角坐标系有多种方法.
例1 对于边长为4的等边三角形ABC(如左下图所示),建立适当的直角坐标系,写出各个顶点的坐标.
【方法归纳】同一图形在不同坐标系中的位置不同,关键点的坐标也不同.
在一次“寻宝”游戏中,寻宝人已经找到了A(3,2)和B(3,-2)两个标志点,并且知道藏宝地点的坐标为(4,4),除此之外不知道其他信息.如何确定直角坐标系找到“宝藏” 与同伴进行交流.
【方法归纳】根据点的坐标的符号特征可以判定点的位置,反之,也可以根据点在直角坐标系中的位置判断其坐标符号的情况.
三.尝试应用:
1.某地为了发展城市群,在现有的四个中小城市A,B,C,D附近新建机场E,试建立适当的直角坐标系,并写出各点的坐标.
2.正方形的边长为2,建立合适的直角坐标系,写出各顶点的坐标 .
四.自主总结:
本节通过学习建立直角坐标系的多种方法,体验数学活动充满着探索与创造,不同的坐标系,对于同一个图形,点的坐标是不同的.
建立不同的平面直角坐标系,同一个图形,同一个点可以用不同的坐标表示,在实际应用中,以坐标简单容易计算为前提.
五.达标测试
1.如图所示的是A,B,C,D四位同学的家所在位置,若以A同学家的位置为坐标原点建立平面直角坐标系,那么C同学家的位置的坐标为(1,5),则B,D两同学家的坐标分别为 ( )
A.(2,3),(3,2) B.(3,2),(2,3) C.(2,3),(-3,2) D.(3,2),(-2,3)
2.如图所示,若“帅”位于点(1,-2)上,“相”位于点(3,-2)上,则“炮”位于点 .
3.如图所示,若点E的坐标为(-2,1),点F的坐标为(1,-1),则点G的坐标为 .
4.星期天,小王、小李、小张三位同学相约到文化广场游玩,出发前,他们每人带了一张利用平面直角坐标系画的示意图(如图所示),其中行政办公楼的坐标是(-4,3),南城百货的坐标是(2,-3).
(1)图中省略了平面直角坐标系,请根据上述信息,画出这个平面直角坐标系;
(2)写出图中体育馆、升旗台、北部湾俱乐部、盘龙苑小区、国际大酒店的坐标;
(3)小王、小张两人到了升旗台附近,这时还没看到小李,于是打电话问小李的位置,小李说他现在位置的坐标是(-2,-2),请在图中用字母A标出小李的位置.
5.在平面直角坐标系中,点A的坐标(-3,4),点B的坐标是(-1,-2),点O为坐标原点,求ΔAOB的面积.
如图所示,正方形ABCD的边长为10,连接各边的中点E,F,G,H得到正方形EFGH,请你建立适当的坐标系,分别写出A,B,C,D,E,F,G,H的坐标.
例题答案
例 解:如图所示,以边BC所在的直线为x轴,以边BC的中垂线为y轴建立直角坐标系.
由等边三角形的性质可知AO=2,等边三角形ABC各个顶点A,B,C的坐标分别为A(0,2),B(-2,0),C(2,0).
三.尝试应用答案
1.解:答案不唯一,可以以点A为坐标原点,建立平面直角坐标系.
2.解:答案不唯一,如图(1)所示,A(0,2),B(2,2),C(2,0),O(0,0);
如图(2)所示,A(-1,1),B(1,1),C(1,-1),D(-1,-1);
如图(3)所示,A(-2,2),B(0,2),D(-2,0),O(0,0);
如图(4)所示,A(-,0),B(0,),C(,0),D(0,-).
达标测试答案
1.D(解析:建立正确的平面直角坐标系,然后确定B,D两家的坐标.)
2.(-2,1)(解析:由“帅”位于点(1,-2),“相”位于点(3,-2),确定平面直角坐标系,再找到“炮”的位置,写出它的坐标.)
3.(1,2)
4.解:(1)建立平面直角坐标系如图所示. (2)体育馆(-9,4),升旗台(-4,2),北部湾俱乐部(-7,-1),盘龙苑小区(-5,-3),国际大酒店(0,0).
(3)小李的位置是如图所示的A点.
5.解:ΔAOB的面积是5.
6.解:答案不唯一,如:以EG所在直线为x轴,以FH所在直线为y轴,建立如图所示的坐标系,则A(-5,-5),B(5,-5),C(5,5),D(-5,5),E(-5,0),F(0,-5),G(5,0),H(0,5).
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
