人教版数学八年级上册 12.2 三角形全等的判定 第2课时 SAS导学案(含答案)
文档属性
| 名称 | 人教版数学八年级上册 12.2 三角形全等的判定 第2课时 SAS导学案(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 86.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-15 00:00:00 | ||
图片预览

文档简介
第十二章 全等三角形
12.2.2 SAS
学习目标
1.能自己试验探索出判定三角形全等的条件:边角边公理.
2.会应用判定方法SAS进行简单的推理判定两个三角形全等.
学习策略
1.通过画符合条件的三角形,理解三角形全等的判定;
2.牢记三角形全等的判定方法.
学习过程
一.复习回顾:
1.怎样的两个三角形是全等三角形? 2.全等三角形的性质?
2.三角形的判定定理的内容?
二.新课学习:
知识点一:三角形全等的判定方法2:“边角边”
阅读课本本节课的内容,解决下列问题.
1.如果已知三角形的两边及一角,那么有哪几种可能
【答案】两种;两边和两边的夹角;两边和其中一边的对角
2.已知线段a=4 cm,b=6 cm,∠α=30°,在硬纸片上用直尺和圆规作出△ABC,使BC=a,AC=b,∠C=∠α,并填一填:
(1)作∠MCN=∠ ;(2)在射线CM上截取BC= ,在射线CN上截取 = ;
(3)连接线段 .
【答案】(1)α (2)a;AC;b (3)AB
3.把你画的三角形与其他同学画的三角形进行比较,全等吗 三角形的两条边的长度和它们的夹角的大小确定了,这个三角形的形状、大小是否唯一确定了
【答案】全等;确定
综之: 和它们的 分别相等的两个三角形全等(简写:“ ”或“ ”).
【答案】两边;夹角;边角边;SAS
4.两条边分别为2.5 cm,3.5 cm,长度为2.5 cm的边所对的角为40°,剪下你画出的三角形,与其他同学剪的三角形进行比较,这些三角形一定能重合吗 由此你发现了什么
【答案】不一定重合;有两边和其中一边的对角分别相等的两个三角形不一定全等
三.尝试应用:
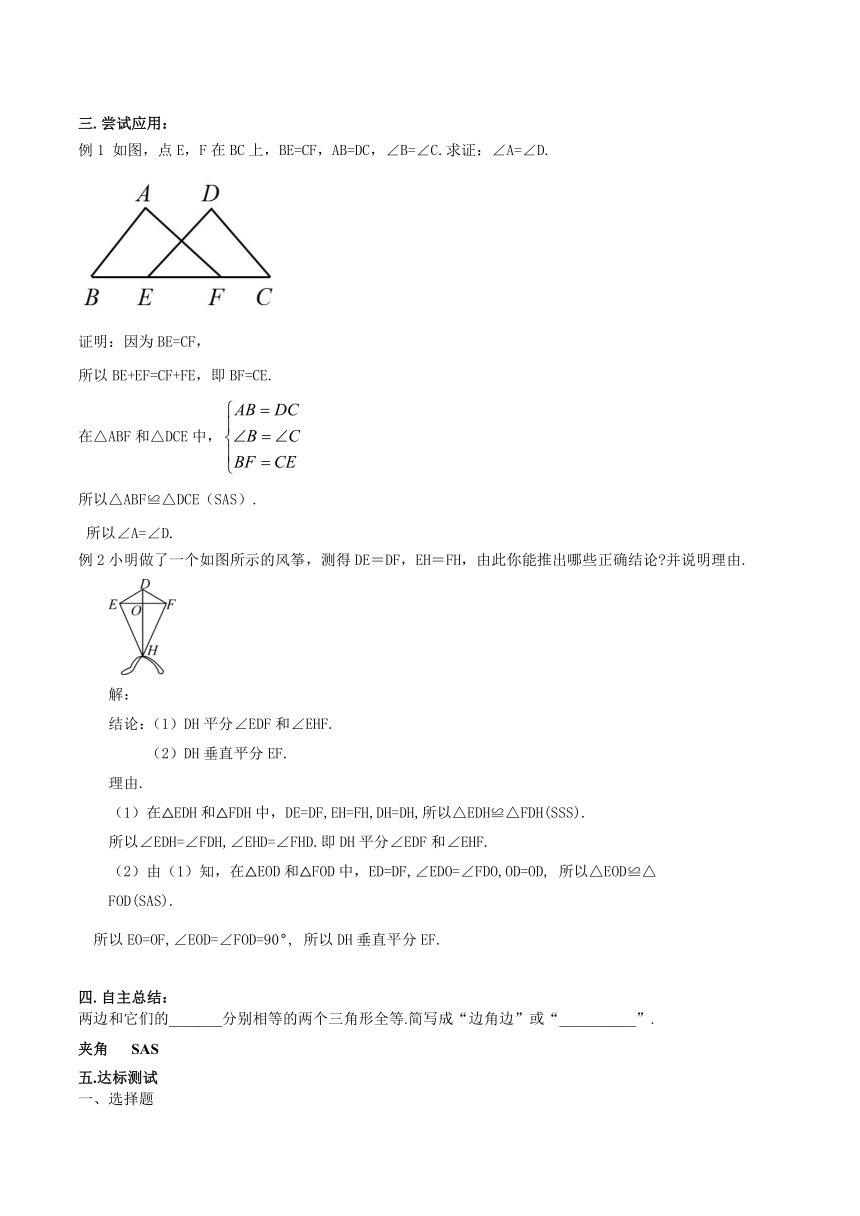
例1 如图,点E,F在BC上,BE=CF,AB=DC,∠B=∠C.求证:∠A=∠D.
证明:因为BE=CF,
所以BE+EF=CF+FE,即BF=CE.
在△ABF和△DCE中,
所以△ABF≌△DCE(SAS).
所以∠A=∠D.
例2小明做了一个如图所示的风筝,测得DE=DF,EH=FH,由此你能推出哪些正确结论 并说明理由.
解:
结论:(1)DH平分∠EDF和∠EHF.
(2)DH垂直平分EF.
理由.
(1)在△EDH和△FDH中,DE=DF,EH=FH,DH=DH,所以△EDH≌△FDH(SSS).
所以∠EDH=∠FDH,∠EHD=∠FHD.即DH平分∠EDF和∠EHF.
(2)由(1)知,在△EOD和△FOD中,ED=DF,∠EDO=∠FDO,OD=OD, 所以△EOD≌△
FOD(SAS).
所以EO=OF,∠EOD=∠FOD=90°, 所以DH垂直平分EF.
四.自主总结:
两边和它们的_______分别相等的两个三角形全等.简写成“边角边”或“__________”.
夹角 SAS
五.达标测试
一、选择题
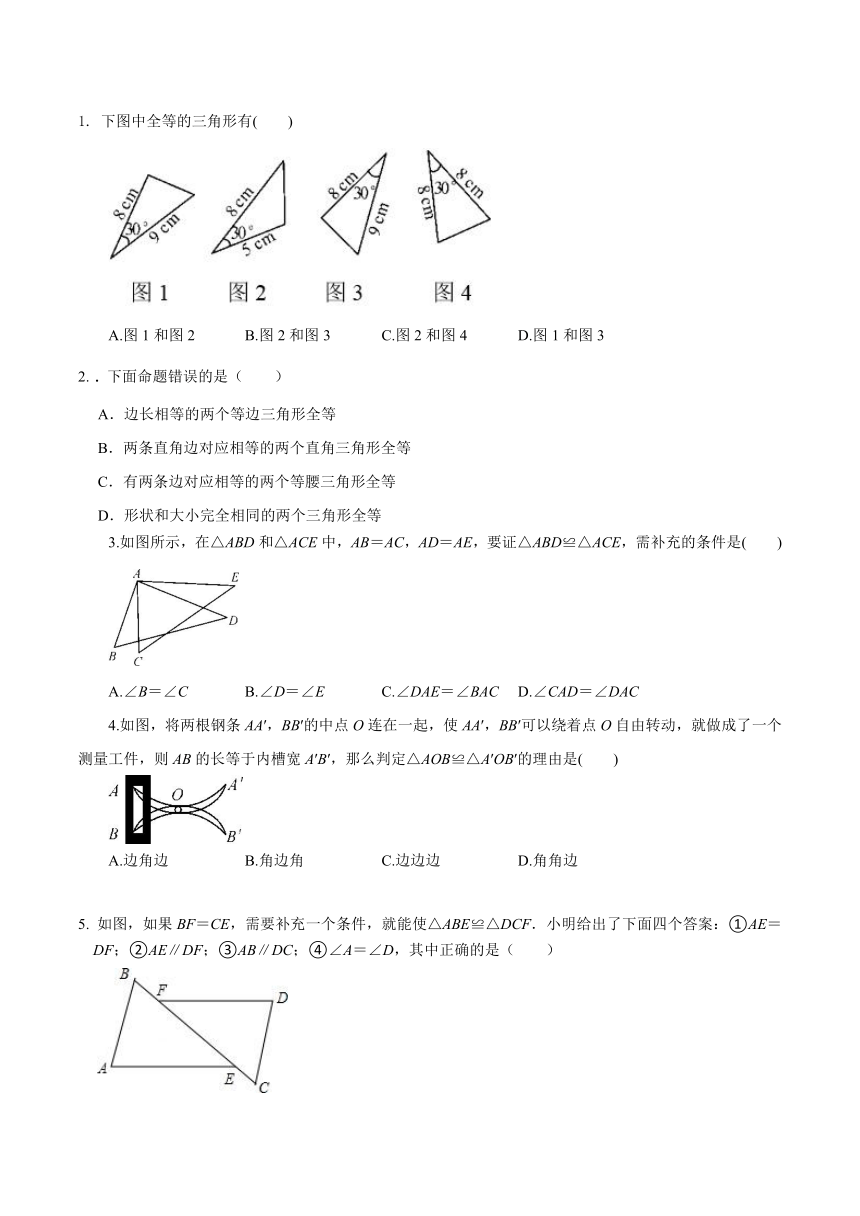
1. 下图中全等的三角形有( )
A.图1和图2 B.图2和图3 C.图2和图4 D.图1和图3
2. . 下面命题错误的是( )
A.边长相等的两个等边三角形全等
B.两条直角边对应相等的两个直角三角形全等
C.有两条边对应相等的两个等腰三角形全等
D.形状和大小完全相同的两个三角形全等
3.如图所示,在△ABD和△ACE中,AB=AC,AD=AE,要证△ABD≌△ACE,需补充的条件是( )
A.∠B=∠C B.∠D=∠E C.∠DAE=∠BAC D.∠CAD=∠DAC
4.如图,将两根钢条AA′,BB′的中点O连在一起,使AA′,BB′可以绕着点O自由转动,就做成了一个测量工件,则AB的长等于内槽宽A′B′,那么判定△AOB≌△A′OB′的理由是( )
A.边角边 B.角边角 C.边边边 D.角角边
5. 如图,如果BF=CE,需要补充一个条件,就能使△ABE≌△DCF.小明给出了下面四个答案:①AE=DF;②AE∥DF;③AB∥DC;④∠A=∠D,其中正确的是( )
A.①②③④ B.①②③ C.①② D.①③
二、填空题
6. 如图,点B在AE上,点D在AC上,AB=AD.请你添加一个适当的条件,使△ABC≌△ADE(只能添加一个).你添加的条件是 .
7. 如图,在△ABC中,AB=6,BC=5,AC=4,AD平分∠BAC交BC于点D,在AB上截取AE=AC,则△BDE的周长为________.
8.在平面直角坐标系中,点A(2,0),B(0,4),作△BOC,使△BOC与△ABO全等,则点C坐标为__________________________.
三、解答题
9. 已知:如图AB = AC,AD = AE,∠BAC =∠DAE,
求证: △ABD ≌△ACE.
10. 如图所示,在新修的小区中,有一条“Z”字形绿色长廊ABCD,其中AB∥CD,在AB,BC,CD三段绿色长廊上各修一小凉亭E,M,F,且BE=CF,点M是BC的中点,在凉亭M与F之间有一池塘,不能直接到达,要想知道M与F之间的距离,只需要测出线段ME的长度(用两个字母表示线段).这样做合适吗?请说出理由.
参考答案
1. D
2.C解析:A、可以用SSS判定两三角形全等;
B、可以用SAS判定两三角形全等;
C、腰虽然相等,但是夹角不一定相等,所以是错误的;
D、基本就是全等的定义.故选:C.
3. C解:补充∠EAD=∠BAC,
因为∠EAD=∠BAC,
所以∠EAD+∠DAC=∠BAC+∠DAC,
即∠EAC=∠DAB,
在△AEC和△ADB中,
,
所以△ABD≌△ACE(SAS).
故选:C.
4.A解析:因为两钢条中点连在一起做成一个测量工件,
所以OA′=OA,OB′=OB,
因为∠BOA=B′OA′,
所以△AOB≌△B′OA′.
所以AB的长等于内槽宽A'B',
用的是SAS的判定定理.
故选:A.
5. C解析:因为BF=CE,
所以BE=CF.
因为AE∥DF,
所以∠AEF=∠DFC.
在△ABE和△DCF中,
所以△ABE≌△DCF(SAS),
即选项C正确;
因为选项A、B(条件有的多余),
所以选项A、B错误;
根据选项D不能推出两三角形全等,故选:C.
6.解析:添加条件:AE=AC,
因为在△ABC和△ADE中,
所以△ADE≌△ABC(SAS),
故答案为:AE=AC.
7. 7 解析:因为AD是∠BAC的平分线,
所以∠EAD=∠CAD
在△ADE和△ADC中,
,
所以△ADE≌△ADC(SAS),
所以ED=CD,
所以BC=BD+CD=DE+BD=5,
所以△BDE的周长=BE+BD+ED=(6﹣4)+5=7.
8.(2,4)或(﹣2,0)或(﹣2,4).解析:因为点A(2,0),B(0,4),
所以OB=4,OA=2,
因为△BOC与△AOB全等,
所以OB=OB=4,OA=OC=BC′=BC′′=2,
所以C(﹣2,0),C′(﹣2,4),C′′(2,4).
9.证明:因为∠BAC =∠DAE,
所以∠BAC+∠CAD =∠DAE +∠CAD,即∠BAD =∠CAE,
在△ABD和△ACE中,
所以△ABD≌△ACE(SAS).
10.合适,理由如下:
因为AB∥CD,
所以∠B=∠C,
因为点M是BC的中点,
所以MB=MC,
在△MEB与△MCF中
,
所以△MEB≌△MFC(SAS),
所以ME=MF,
所以想知道M与F之间的距离,只需要测出线段ME的长度.
12.2.2 SAS
学习目标
1.能自己试验探索出判定三角形全等的条件:边角边公理.
2.会应用判定方法SAS进行简单的推理判定两个三角形全等.
学习策略
1.通过画符合条件的三角形,理解三角形全等的判定;
2.牢记三角形全等的判定方法.
学习过程
一.复习回顾:
1.怎样的两个三角形是全等三角形? 2.全等三角形的性质?
2.三角形的判定定理的内容?
二.新课学习:
知识点一:三角形全等的判定方法2:“边角边”
阅读课本本节课的内容,解决下列问题.
1.如果已知三角形的两边及一角,那么有哪几种可能
【答案】两种;两边和两边的夹角;两边和其中一边的对角
2.已知线段a=4 cm,b=6 cm,∠α=30°,在硬纸片上用直尺和圆规作出△ABC,使BC=a,AC=b,∠C=∠α,并填一填:
(1)作∠MCN=∠ ;(2)在射线CM上截取BC= ,在射线CN上截取 = ;
(3)连接线段 .
【答案】(1)α (2)a;AC;b (3)AB
3.把你画的三角形与其他同学画的三角形进行比较,全等吗 三角形的两条边的长度和它们的夹角的大小确定了,这个三角形的形状、大小是否唯一确定了
【答案】全等;确定
综之: 和它们的 分别相等的两个三角形全等(简写:“ ”或“ ”).
【答案】两边;夹角;边角边;SAS
4.两条边分别为2.5 cm,3.5 cm,长度为2.5 cm的边所对的角为40°,剪下你画出的三角形,与其他同学剪的三角形进行比较,这些三角形一定能重合吗 由此你发现了什么
【答案】不一定重合;有两边和其中一边的对角分别相等的两个三角形不一定全等
三.尝试应用:
例1 如图,点E,F在BC上,BE=CF,AB=DC,∠B=∠C.求证:∠A=∠D.
证明:因为BE=CF,
所以BE+EF=CF+FE,即BF=CE.
在△ABF和△DCE中,
所以△ABF≌△DCE(SAS).
所以∠A=∠D.
例2小明做了一个如图所示的风筝,测得DE=DF,EH=FH,由此你能推出哪些正确结论 并说明理由.
解:
结论:(1)DH平分∠EDF和∠EHF.
(2)DH垂直平分EF.
理由.
(1)在△EDH和△FDH中,DE=DF,EH=FH,DH=DH,所以△EDH≌△FDH(SSS).
所以∠EDH=∠FDH,∠EHD=∠FHD.即DH平分∠EDF和∠EHF.
(2)由(1)知,在△EOD和△FOD中,ED=DF,∠EDO=∠FDO,OD=OD, 所以△EOD≌△
FOD(SAS).
所以EO=OF,∠EOD=∠FOD=90°, 所以DH垂直平分EF.
四.自主总结:
两边和它们的_______分别相等的两个三角形全等.简写成“边角边”或“__________”.
夹角 SAS
五.达标测试
一、选择题
1. 下图中全等的三角形有( )
A.图1和图2 B.图2和图3 C.图2和图4 D.图1和图3
2. . 下面命题错误的是( )
A.边长相等的两个等边三角形全等
B.两条直角边对应相等的两个直角三角形全等
C.有两条边对应相等的两个等腰三角形全等
D.形状和大小完全相同的两个三角形全等
3.如图所示,在△ABD和△ACE中,AB=AC,AD=AE,要证△ABD≌△ACE,需补充的条件是( )
A.∠B=∠C B.∠D=∠E C.∠DAE=∠BAC D.∠CAD=∠DAC
4.如图,将两根钢条AA′,BB′的中点O连在一起,使AA′,BB′可以绕着点O自由转动,就做成了一个测量工件,则AB的长等于内槽宽A′B′,那么判定△AOB≌△A′OB′的理由是( )
A.边角边 B.角边角 C.边边边 D.角角边
5. 如图,如果BF=CE,需要补充一个条件,就能使△ABE≌△DCF.小明给出了下面四个答案:①AE=DF;②AE∥DF;③AB∥DC;④∠A=∠D,其中正确的是( )
A.①②③④ B.①②③ C.①② D.①③
二、填空题
6. 如图,点B在AE上,点D在AC上,AB=AD.请你添加一个适当的条件,使△ABC≌△ADE(只能添加一个).你添加的条件是 .
7. 如图,在△ABC中,AB=6,BC=5,AC=4,AD平分∠BAC交BC于点D,在AB上截取AE=AC,则△BDE的周长为________.
8.在平面直角坐标系中,点A(2,0),B(0,4),作△BOC,使△BOC与△ABO全等,则点C坐标为__________________________.
三、解答题
9. 已知:如图AB = AC,AD = AE,∠BAC =∠DAE,
求证: △ABD ≌△ACE.
10. 如图所示,在新修的小区中,有一条“Z”字形绿色长廊ABCD,其中AB∥CD,在AB,BC,CD三段绿色长廊上各修一小凉亭E,M,F,且BE=CF,点M是BC的中点,在凉亭M与F之间有一池塘,不能直接到达,要想知道M与F之间的距离,只需要测出线段ME的长度(用两个字母表示线段).这样做合适吗?请说出理由.
参考答案
1. D
2.C解析:A、可以用SSS判定两三角形全等;
B、可以用SAS判定两三角形全等;
C、腰虽然相等,但是夹角不一定相等,所以是错误的;
D、基本就是全等的定义.故选:C.
3. C解:补充∠EAD=∠BAC,
因为∠EAD=∠BAC,
所以∠EAD+∠DAC=∠BAC+∠DAC,
即∠EAC=∠DAB,
在△AEC和△ADB中,
,
所以△ABD≌△ACE(SAS).
故选:C.
4.A解析:因为两钢条中点连在一起做成一个测量工件,
所以OA′=OA,OB′=OB,
因为∠BOA=B′OA′,
所以△AOB≌△B′OA′.
所以AB的长等于内槽宽A'B',
用的是SAS的判定定理.
故选:A.
5. C解析:因为BF=CE,
所以BE=CF.
因为AE∥DF,
所以∠AEF=∠DFC.
在△ABE和△DCF中,
所以△ABE≌△DCF(SAS),
即选项C正确;
因为选项A、B(条件有的多余),
所以选项A、B错误;
根据选项D不能推出两三角形全等,故选:C.
6.解析:添加条件:AE=AC,
因为在△ABC和△ADE中,
所以△ADE≌△ABC(SAS),
故答案为:AE=AC.
7. 7 解析:因为AD是∠BAC的平分线,
所以∠EAD=∠CAD
在△ADE和△ADC中,
,
所以△ADE≌△ADC(SAS),
所以ED=CD,
所以BC=BD+CD=DE+BD=5,
所以△BDE的周长=BE+BD+ED=(6﹣4)+5=7.
8.(2,4)或(﹣2,0)或(﹣2,4).解析:因为点A(2,0),B(0,4),
所以OB=4,OA=2,
因为△BOC与△AOB全等,
所以OB=OB=4,OA=OC=BC′=BC′′=2,
所以C(﹣2,0),C′(﹣2,4),C′′(2,4).
9.证明:因为∠BAC =∠DAE,
所以∠BAC+∠CAD =∠DAE +∠CAD,即∠BAD =∠CAE,
在△ABD和△ACE中,
所以△ABD≌△ACE(SAS).
10.合适,理由如下:
因为AB∥CD,
所以∠B=∠C,
因为点M是BC的中点,
所以MB=MC,
在△MEB与△MCF中
,
所以△MEB≌△MFC(SAS),
所以ME=MF,
所以想知道M与F之间的距离,只需要测出线段ME的长度.
