人教版数学七年级上册 4.2直线、射线、线段的概念 (3)课件 (共16张ppt)
文档属性
| 名称 | 人教版数学七年级上册 4.2直线、射线、线段的概念 (3)课件 (共16张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 518.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-15 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
第四章 几何图形初步
4.2 直线、射线、线段的概念
第3课时
学习目标
理解“两点之间,线段最短”的结论,并能用这一结论解释一些简单的问题.
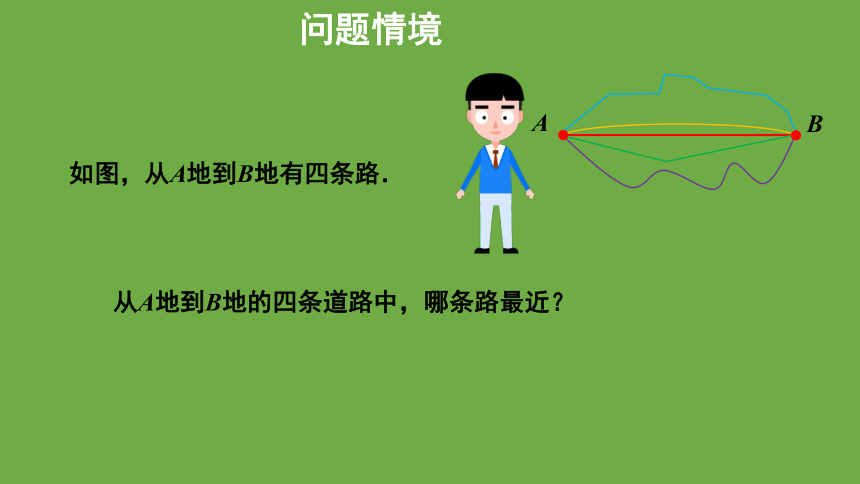
如图,从A地到B地有四条路.
从A地到B地的四条道路中,哪条路最近?
A
B
问题情境
我们在生活中有时经常见到行人为穿越马路而跨越栏杆的景象,他们为什么这样做?
问题情境
问题情境
问题情境
A
B
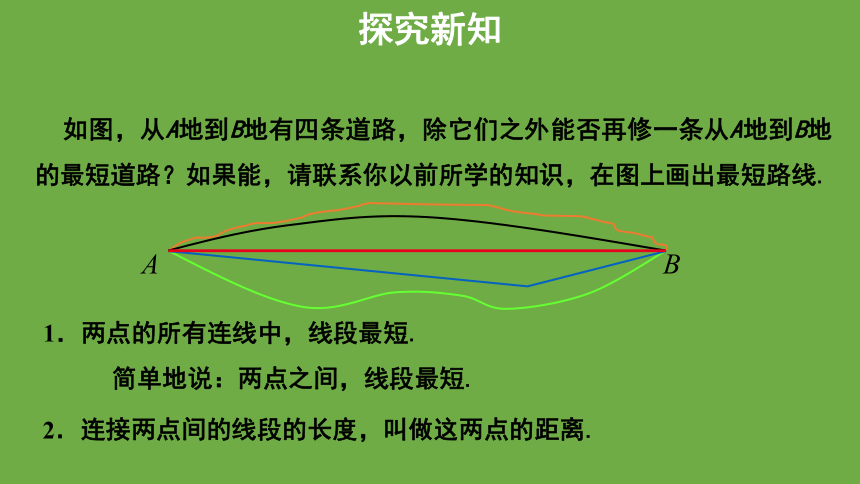
如图,从A地到B地有四条道路,除它们之外能否再修一条从A地到B地的最短道路?如果能,请联系你以前所学的知识,在图上画出最短路线.
1.两点的所有连线中,线段最短.
简单地说:两点之间,线段最短.
2.连接两点间的线段的长度,叫做这两点的距离.
探究新知
例1.如图,一只蚂蚁要从正方形的一个顶点A爬到顶点B,怎样爬距离最短?
解:根据线段的性质“两点之间,线段最短”可得沿线段AB爬行路线最短.
典型例题
例2.(1)如图,把原来弯曲的河道改直,A,B两地间的河道长度有什么变化?
(2)如图,公园里修建了曲折迂回的桥,这与修一座直的桥相比,对游人观赏湖面风光能起什么作用?用你所学数学知识说明其中的道理.
典型例题
两点之间,线段最短.
河道长度变短
典型例题
3.1拃是拇指和食指在平面上伸直时,两者端点之间的距离.则以下估计正确的是( ).
A.课本的宽度约4拃 B.课桌的高度约为4拃
C.黑板的长度约为4拃 D.字典的厚度约为4拃
4.在修建崇钦高速公路时,有时需要将弯曲的道路改直,依据
是 .
B
两点之间,线段最短
典型例题
5.小明家在A处,学校在C处,从A-B-C是宽敞的马路,从A-C是一条小路,小明上学时,经常不走马路而走小路,有人说:“这孩子真淘气,放着宽敞的大道不走偏走小路.”小明对他解释一番后,这个人恍然大悟,你知道小明怎样解释的吗?
利用“两点之间,线段最短”的原理解释.
1.一条河流两旁有两个村庄A,B,现需要架一座桥,使它到A , B两村的距离最短,应怎样选址?
解:连接AB,交河l于P点,点P即为所求.
P
课堂练习
2.你能说出从B到C可行的路线吗?哪条最短呢?从A到B呢?
解:从B到C有两条路:B-A-C,BC . BC最短.
从A到B也有两条路:A-C-B , AB . AB最短.
课堂练习
3.如图,A,B,C三个城市在同一直线上,A到B有三条道路,B到C有两条道路,试分析从A经B到C的走法有几种,用笔描出哪种最近.
解: 6种; 最近的是A-B-C.
课堂练习
1.两点之间,线段最短.
2.两点间的距离:连接两点的线段的长度叫两点间的距离.
课堂小结
再见
第四章 几何图形初步
4.2 直线、射线、线段的概念
第3课时
学习目标
理解“两点之间,线段最短”的结论,并能用这一结论解释一些简单的问题.
如图,从A地到B地有四条路.
从A地到B地的四条道路中,哪条路最近?
A
B
问题情境
我们在生活中有时经常见到行人为穿越马路而跨越栏杆的景象,他们为什么这样做?
问题情境
问题情境
问题情境
A
B
如图,从A地到B地有四条道路,除它们之外能否再修一条从A地到B地的最短道路?如果能,请联系你以前所学的知识,在图上画出最短路线.
1.两点的所有连线中,线段最短.
简单地说:两点之间,线段最短.
2.连接两点间的线段的长度,叫做这两点的距离.
探究新知
例1.如图,一只蚂蚁要从正方形的一个顶点A爬到顶点B,怎样爬距离最短?
解:根据线段的性质“两点之间,线段最短”可得沿线段AB爬行路线最短.
典型例题
例2.(1)如图,把原来弯曲的河道改直,A,B两地间的河道长度有什么变化?
(2)如图,公园里修建了曲折迂回的桥,这与修一座直的桥相比,对游人观赏湖面风光能起什么作用?用你所学数学知识说明其中的道理.
典型例题
两点之间,线段最短.
河道长度变短
典型例题
3.1拃是拇指和食指在平面上伸直时,两者端点之间的距离.则以下估计正确的是( ).
A.课本的宽度约4拃 B.课桌的高度约为4拃
C.黑板的长度约为4拃 D.字典的厚度约为4拃
4.在修建崇钦高速公路时,有时需要将弯曲的道路改直,依据
是 .
B
两点之间,线段最短
典型例题
5.小明家在A处,学校在C处,从A-B-C是宽敞的马路,从A-C是一条小路,小明上学时,经常不走马路而走小路,有人说:“这孩子真淘气,放着宽敞的大道不走偏走小路.”小明对他解释一番后,这个人恍然大悟,你知道小明怎样解释的吗?
利用“两点之间,线段最短”的原理解释.
1.一条河流两旁有两个村庄A,B,现需要架一座桥,使它到A , B两村的距离最短,应怎样选址?
解:连接AB,交河l于P点,点P即为所求.
P
课堂练习
2.你能说出从B到C可行的路线吗?哪条最短呢?从A到B呢?
解:从B到C有两条路:B-A-C,BC . BC最短.
从A到B也有两条路:A-C-B , AB . AB最短.
课堂练习
3.如图,A,B,C三个城市在同一直线上,A到B有三条道路,B到C有两条道路,试分析从A经B到C的走法有几种,用笔描出哪种最近.
解: 6种; 最近的是A-B-C.
课堂练习
1.两点之间,线段最短.
2.两点间的距离:连接两点的线段的长度叫两点间的距离.
课堂小结
再见
