数学人教版 七年级上册 1.5.3 近似数优质教学课件(共17张ppt)
文档属性
| 名称 | 数学人教版 七年级上册 1.5.3 近似数优质教学课件(共17张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 246.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-15 09:22:34 | ||
图片预览






文档简介
(共17张PPT)
1.5.3 近似数
第一章 有理数
学习目标
1.了解近似数的意义,并体会它在生活中的应用;
2.会区别准确数和近似数,理解精确度的意义;
3.能够按要求取近似数并会求近似数的精确度.
一、创设情境,探究新知
根据自己的生活经验,观察身边熟悉的事物,收集一些数据:
(1)我班有 名学生, 名男生, 名女生;
(2)一天有 小时,1小时有 分钟,1分钟有 秒;
(3)你的身高约为 cm,体重约为 kg.
在上面这些数据中,那些数是与实际完全符合的?哪些数是与实际接近的?
一、创设情境,探究新知
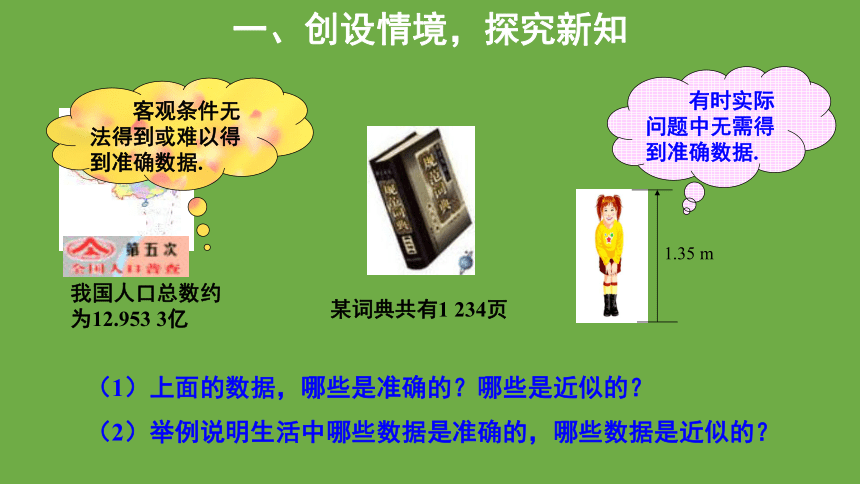
我国人口总数约为12.953 3亿
某词典共有1 234页
1.35 m
(1)上面的数据,哪些是准确的?哪些是近似的?
客观条件无法得到或难以得到准确数据.
有时实际问题中无需得到准确数据.
(2)举例说明生活中哪些数据是准确的,哪些数据是近似的?
二、理解概念
准确数与近似数
准确数是与实际相符的数;
近似数是接近实际数但与实际数有差别的数.
注意:(1)测量、称量所得的数据都是近似数,在实际情况下得出的大约数也是近似数;
(2)识别近似数与准确数的方法:
①语句中带有“约”“左右”等词语,里面出现的数据是近似数;
②描述“温度”“身高”“体重”的数据是近似数.
二、理解概念
下列各题中的数据,哪些是准确数,哪些是近似数?
(1)通过第三次全国人口普查得知,某省人口总数为3297万;
(2)生物圈中,已知绿色植物约有30万种;
(3)某校有1148人;
(4)这个路口每分钟有3人经过.
解:(1)3297万是近似数; (2)30万是近似数;
(3)1148是准确数; (4)3是近似数.
三、深入探究
近似数的精确度
近似数与准确数的接近程度,可以用精确度表示.
注意:精确度的确定方法:
①一般地,一个近似数,四舍五入到哪一位,就说这个近似数精确到哪一位;
②精确度是近似数的最后一位,最后一位在哪位上,就说这个近似数精确到哪一位.
如近似数3206.828的精确度是精确到0.001,
或精确到千分位.
③特别地,带有“万”“亿”等计数单位的近似数,看精确到哪一位,要先把带有单位的数恢复成原数,然后看近似数的末位在原数的哪一位上,这个数就精确到哪一位.
如9.86万是精确到百位,而不是百分位.
四、综合运用
用四舍五入法求近似数
用四舍五入法,按括号中的要求对下列各数取近似数.
(1)0.03049(精确到0.001);
(2)199.5(精确到个位);
(3)48.396(精确到百分位);
(4)67294(精确到万位).
(1)0.03049≈0.030;
解:
(2)199.5 ≈ 200;
(3)48.396 ≈ 48.40;
(4)67294 ≈7×104
或67294 ≈7万.
“0.030”与“48.40”中的末位0能否去掉?
四、综合运用
用四舍五入法求近似数
①若一个近似数M的值为3.56,则它可记作M≈3.56.
这里“≈”读作“约等于”或“近似于”.
②近似数小数点后的0不能随便省略,以便区别其精确度;
(1)0.03049≈0.030;
(3)48.396 ≈ 48.40;
③取近似值时,小数点后面的数可以直接四舍五入,但小数点前面的数不能直接四舍五入,应先用科学记数法将要四舍五入的数放在小数点的后面,然后再四舍五入.
四、综合运用
按四舍五入法对圆周率π取近似值时,有
π≈3(精确到个位),
π≈3.1(精确到0.1,或叫做精确到十分位),
π≈3.14(精确到0.01,或叫做精确到百分位),
π≈3.142(精确到 ,或叫做精确到 ),
π≈3.141 6(精确到 ,或叫做精确到 ).
·······
0.001
千分位
0.000 1
万分位
五、例题精析
例1 下列由四舍五入法得到的近似数,各精确到哪一位?有几个有效数字?
(1)132.4精确到___________,
(2) 0.057 2精确到____________,
(3)2.4 万精确到______________,
(4)2.4×104精确到______________.
十分位
万分位
千位
千位
五、例题精析
例2 用四舍五入法,按括号中的要求对下列各数取近似数.
(1)0.344 82(精确到百分位);
解:0.344 82 ≈0.34;
(2)1.504 6(精确到0.01);
解:1.504 6 ≈1.50;
(3)30 542(精确到百位).
解:30 542 ≈3.05×104.
小窍门
当四舍五入到十位或十位以上时,应先用科学记数法表示这个数,再按要求取近似数.
五、例题精析
例3 李明测得一根钢管的长度约为0.8 m.
(1)试举例说明该近似数可能是由哪些数四舍五入得来的?
(2)按照李明测得的结果,你能求出钢管的准确长度x应在什么范围吗?
答:0.75≤x<0.85
六、课堂演练
基础演练
一般取 ;
这是一个 数.
2.下列近似数,各精确到哪一位?
(1)127.32 (2)0.0407 (3)203.0 (4)4.002
3.用四舍五入法,对下列各数按要求取近似数.
(1)9.03456(精确到0.0001);(2)5678999(精确到万位).
4.某市2017年财政收入取得重大突破,地方公共财政收入用四舍五入取近似值后为27.39亿元,那么这个数值( )
A. 精确到亿位
B. 精确到百分位
C. 精确到千万位
D. 精确到百万位
D
六、课堂演练
5.若用四舍五入法取得的近似数4.3的准确值为k,求k的取值范围.
能力提升
解:4.25≤k<4.35
规律:一般地,如果一个数m的近似数a,
则m的取值范围是a-05≤m<a+0.5.
七、课堂小结
1.近似数与准确数
准确数是与实际相符的数;
近似数是接近实际数但与实际数有差别的数.
2.近似数的精确度
近似数与准确数的接近程度,可以用精确度表示.
3.用四舍五入法求近似数
(1)近似数小数点后的0不能随便省略,以便区别其精确度;
(2)取近似值时,小数点后面的数可以直接四舍五入,但小数点前面的数不能直接四舍五入,应先用科学记数法将要四舍五入的数放在小数点的后面,然后再四舍五入.
再见
1.5.3 近似数
第一章 有理数
学习目标
1.了解近似数的意义,并体会它在生活中的应用;
2.会区别准确数和近似数,理解精确度的意义;
3.能够按要求取近似数并会求近似数的精确度.
一、创设情境,探究新知
根据自己的生活经验,观察身边熟悉的事物,收集一些数据:
(1)我班有 名学生, 名男生, 名女生;
(2)一天有 小时,1小时有 分钟,1分钟有 秒;
(3)你的身高约为 cm,体重约为 kg.
在上面这些数据中,那些数是与实际完全符合的?哪些数是与实际接近的?
一、创设情境,探究新知
我国人口总数约为12.953 3亿
某词典共有1 234页
1.35 m
(1)上面的数据,哪些是准确的?哪些是近似的?
客观条件无法得到或难以得到准确数据.
有时实际问题中无需得到准确数据.
(2)举例说明生活中哪些数据是准确的,哪些数据是近似的?
二、理解概念
准确数与近似数
准确数是与实际相符的数;
近似数是接近实际数但与实际数有差别的数.
注意:(1)测量、称量所得的数据都是近似数,在实际情况下得出的大约数也是近似数;
(2)识别近似数与准确数的方法:
①语句中带有“约”“左右”等词语,里面出现的数据是近似数;
②描述“温度”“身高”“体重”的数据是近似数.
二、理解概念
下列各题中的数据,哪些是准确数,哪些是近似数?
(1)通过第三次全国人口普查得知,某省人口总数为3297万;
(2)生物圈中,已知绿色植物约有30万种;
(3)某校有1148人;
(4)这个路口每分钟有3人经过.
解:(1)3297万是近似数; (2)30万是近似数;
(3)1148是准确数; (4)3是近似数.
三、深入探究
近似数的精确度
近似数与准确数的接近程度,可以用精确度表示.
注意:精确度的确定方法:
①一般地,一个近似数,四舍五入到哪一位,就说这个近似数精确到哪一位;
②精确度是近似数的最后一位,最后一位在哪位上,就说这个近似数精确到哪一位.
如近似数3206.828的精确度是精确到0.001,
或精确到千分位.
③特别地,带有“万”“亿”等计数单位的近似数,看精确到哪一位,要先把带有单位的数恢复成原数,然后看近似数的末位在原数的哪一位上,这个数就精确到哪一位.
如9.86万是精确到百位,而不是百分位.
四、综合运用
用四舍五入法求近似数
用四舍五入法,按括号中的要求对下列各数取近似数.
(1)0.03049(精确到0.001);
(2)199.5(精确到个位);
(3)48.396(精确到百分位);
(4)67294(精确到万位).
(1)0.03049≈0.030;
解:
(2)199.5 ≈ 200;
(3)48.396 ≈ 48.40;
(4)67294 ≈7×104
或67294 ≈7万.
“0.030”与“48.40”中的末位0能否去掉?
四、综合运用
用四舍五入法求近似数
①若一个近似数M的值为3.56,则它可记作M≈3.56.
这里“≈”读作“约等于”或“近似于”.
②近似数小数点后的0不能随便省略,以便区别其精确度;
(1)0.03049≈0.030;
(3)48.396 ≈ 48.40;
③取近似值时,小数点后面的数可以直接四舍五入,但小数点前面的数不能直接四舍五入,应先用科学记数法将要四舍五入的数放在小数点的后面,然后再四舍五入.
四、综合运用
按四舍五入法对圆周率π取近似值时,有
π≈3(精确到个位),
π≈3.1(精确到0.1,或叫做精确到十分位),
π≈3.14(精确到0.01,或叫做精确到百分位),
π≈3.142(精确到 ,或叫做精确到 ),
π≈3.141 6(精确到 ,或叫做精确到 ).
·······
0.001
千分位
0.000 1
万分位
五、例题精析
例1 下列由四舍五入法得到的近似数,各精确到哪一位?有几个有效数字?
(1)132.4精确到___________,
(2) 0.057 2精确到____________,
(3)2.4 万精确到______________,
(4)2.4×104精确到______________.
十分位
万分位
千位
千位
五、例题精析
例2 用四舍五入法,按括号中的要求对下列各数取近似数.
(1)0.344 82(精确到百分位);
解:0.344 82 ≈0.34;
(2)1.504 6(精确到0.01);
解:1.504 6 ≈1.50;
(3)30 542(精确到百位).
解:30 542 ≈3.05×104.
小窍门
当四舍五入到十位或十位以上时,应先用科学记数法表示这个数,再按要求取近似数.
五、例题精析
例3 李明测得一根钢管的长度约为0.8 m.
(1)试举例说明该近似数可能是由哪些数四舍五入得来的?
(2)按照李明测得的结果,你能求出钢管的准确长度x应在什么范围吗?
答:0.75≤x<0.85
六、课堂演练
基础演练
一般取 ;
这是一个 数.
2.下列近似数,各精确到哪一位?
(1)127.32 (2)0.0407 (3)203.0 (4)4.002
3.用四舍五入法,对下列各数按要求取近似数.
(1)9.03456(精确到0.0001);(2)5678999(精确到万位).
4.某市2017年财政收入取得重大突破,地方公共财政收入用四舍五入取近似值后为27.39亿元,那么这个数值( )
A. 精确到亿位
B. 精确到百分位
C. 精确到千万位
D. 精确到百万位
D
六、课堂演练
5.若用四舍五入法取得的近似数4.3的准确值为k,求k的取值范围.
能力提升
解:4.25≤k<4.35
规律:一般地,如果一个数m的近似数a,
则m的取值范围是a-05≤m<a+0.5.
七、课堂小结
1.近似数与准确数
准确数是与实际相符的数;
近似数是接近实际数但与实际数有差别的数.
2.近似数的精确度
近似数与准确数的接近程度,可以用精确度表示.
3.用四舍五入法求近似数
(1)近似数小数点后的0不能随便省略,以便区别其精确度;
(2)取近似值时,小数点后面的数可以直接四舍五入,但小数点前面的数不能直接四舍五入,应先用科学记数法将要四舍五入的数放在小数点的后面,然后再四舍五入.
再见
