4.2 线段的性质及应用 课件(共17张PPT) 人教版数学七年级上册
文档属性
| 名称 | 4.2 线段的性质及应用 课件(共17张PPT) 人教版数学七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-15 00:00:00 | ||
图片预览




文档简介
(共17张PPT)
师大附中梅溪湖中学七年级备课组
线段的性质及应用
复习回顾
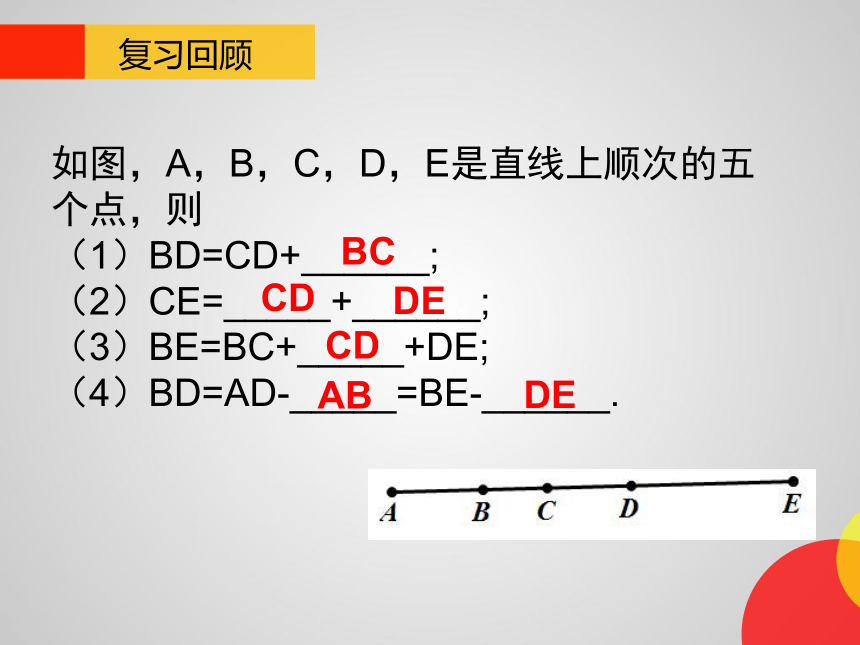
如图,A,B,C,D,E是直线上顺次的五个点,则
(1)BD=CD+______;
(2)CE=_____+______;
(3)BE=BC+_____+DE;
(4)BD=AD-_____=BE-______.
BC
CD
DE
CD
AB
DE
探索新知
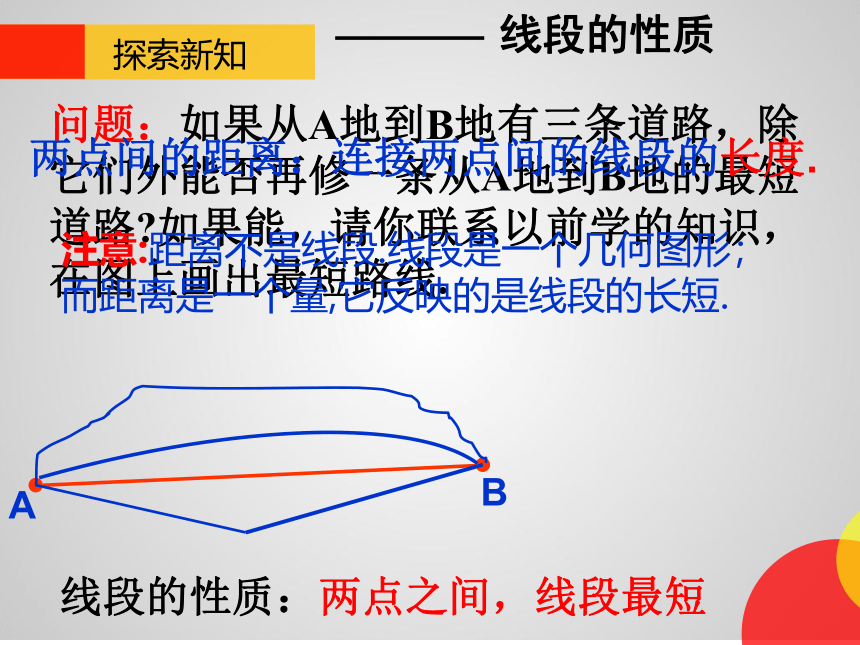
问题:如果从A地到B地有三条道路,除它们外能否再修一条从A地到B地的最短道路 如果能,请你联系以前学的知识,在图上画出最短路线.
线段的性质
线段的性质:两点之间,线段最短
A
B
两点间的距离:连接两点间的线段的长度.
注意:距离不是线段.线段是一个几何图形;而距离是一个量,它反映的是线段的长短.
探索新知
你还能举出类似这样的例子吗?
探索新知
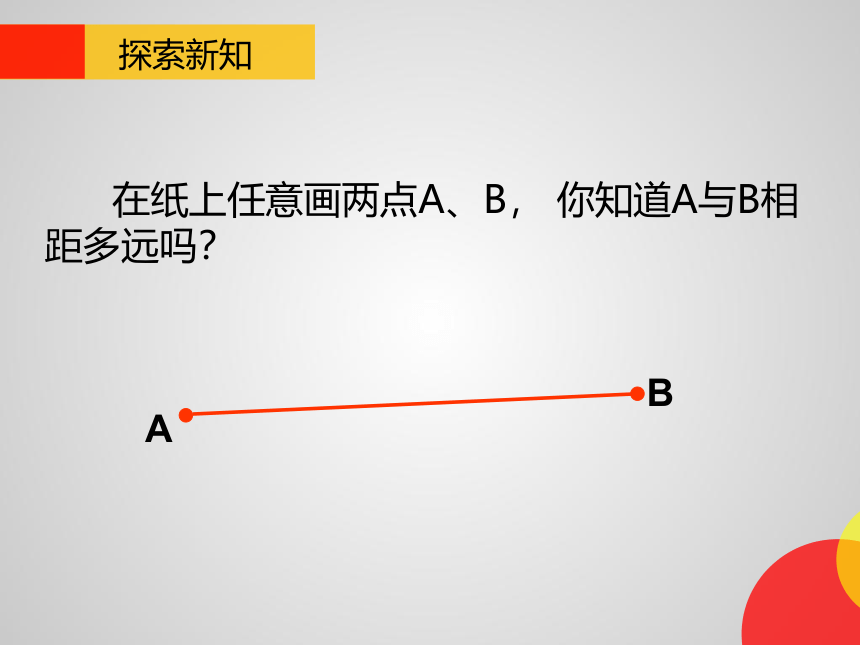
在纸上任意画两点A、B, 你知道A与B相距多远吗?
A
B
探索新知
2、两点之间的距离:
定义:
连接两点间的线段的长度,叫做这
两点的距离.
注意:距离不是线段.线段是一个几何图形;而距离是一个量,它反映的是线段的长短.
A
B
典例分析
C
例1 如图,有一条笔直的公路,公路两旁各有一点C、D表示工厂,要在公路旁建一个货运站,使它到两厂的距离之和最短,问这个货运站应建在何处?说明理由.
解: 把公路看作直线 ,连接CD,交直线 于点E,则E点的位置就是建货运站的位置.因为C、D两点的连线中线段最短.
E
货运站
D
典例分析
例2 如图,一只蚂蚁要从正方体的顶点A沿表面爬行到顶点B,怎样爬行路线最短?
A
B
如果要爬行到顶点C,怎样爬行路线最短?
C
典例分析
A
C
B
B
A
C
C
探索新知
B
C
D
E
A
F
解:
如图,设四个红色旅游区分别为A、B、C、D,连接AC、BD,且线段AC与BD交于点E,即饭店应建在E点位置最合适.
若要在西湖风景区建造一个饭店,为了方便游客,要求是饭店到图中四个红色的旅游区的距离之和最短,请问应该建造在何处?
趣味思考:
习题演练
A
B
练习1:把原来弯曲的河道改直,A、B两地间的河道长度有什么变化?你能用数学知识解释其中的道理吗?
答:A、B两地间的河道长度变为最短.
原理:两点之间,线段最短.
习题演练
练习2 下列说法正确的是( )
A、连接两点的线段叫做两点间的距离.
B、两点间的连线的长度,叫做两点间的距离.
C、连接两点的直线的长度,叫做两点的距离.
D、连接两点的线段的长度,叫做两点间的距离.
D
课堂小结
线段的性质:两点之间,线段最短.
两点的距离:连接两点间的线段的长度,叫做这两点的距离.
1、如图,点C在线段AB上,点D是AC的中点,如果BC= CD,AB=7 cm,求BC的长.
提高练习
2、如图,M、N是线段EF上两点,已知 EA : AB: BF =1:2:3,M、N分别为EA、BF的中点,且MN=8,求EF的长.
E
A
B
N
F
M
x
x
4x
6x
8
3x
提高练习
3、已知线段AB=10,点C在直线AB上,且AC=4,若点D是AB的中点,求DC的长.
情况一:点C在A的左侧
情况二:点C在A的右侧
提高练习
师大附中梅溪湖中学七年级备课组
线段的性质及应用
复习回顾
如图,A,B,C,D,E是直线上顺次的五个点,则
(1)BD=CD+______;
(2)CE=_____+______;
(3)BE=BC+_____+DE;
(4)BD=AD-_____=BE-______.
BC
CD
DE
CD
AB
DE
探索新知
问题:如果从A地到B地有三条道路,除它们外能否再修一条从A地到B地的最短道路 如果能,请你联系以前学的知识,在图上画出最短路线.
线段的性质
线段的性质:两点之间,线段最短
A
B
两点间的距离:连接两点间的线段的长度.
注意:距离不是线段.线段是一个几何图形;而距离是一个量,它反映的是线段的长短.
探索新知
你还能举出类似这样的例子吗?
探索新知
在纸上任意画两点A、B, 你知道A与B相距多远吗?
A
B
探索新知
2、两点之间的距离:
定义:
连接两点间的线段的长度,叫做这
两点的距离.
注意:距离不是线段.线段是一个几何图形;而距离是一个量,它反映的是线段的长短.
A
B
典例分析
C
例1 如图,有一条笔直的公路,公路两旁各有一点C、D表示工厂,要在公路旁建一个货运站,使它到两厂的距离之和最短,问这个货运站应建在何处?说明理由.
解: 把公路看作直线 ,连接CD,交直线 于点E,则E点的位置就是建货运站的位置.因为C、D两点的连线中线段最短.
E
货运站
D
典例分析
例2 如图,一只蚂蚁要从正方体的顶点A沿表面爬行到顶点B,怎样爬行路线最短?
A
B
如果要爬行到顶点C,怎样爬行路线最短?
C
典例分析
A
C
B
B
A
C
C
探索新知
B
C
D
E
A
F
解:
如图,设四个红色旅游区分别为A、B、C、D,连接AC、BD,且线段AC与BD交于点E,即饭店应建在E点位置最合适.
若要在西湖风景区建造一个饭店,为了方便游客,要求是饭店到图中四个红色的旅游区的距离之和最短,请问应该建造在何处?
趣味思考:
习题演练
A
B
练习1:把原来弯曲的河道改直,A、B两地间的河道长度有什么变化?你能用数学知识解释其中的道理吗?
答:A、B两地间的河道长度变为最短.
原理:两点之间,线段最短.
习题演练
练习2 下列说法正确的是( )
A、连接两点的线段叫做两点间的距离.
B、两点间的连线的长度,叫做两点间的距离.
C、连接两点的直线的长度,叫做两点的距离.
D、连接两点的线段的长度,叫做两点间的距离.
D
课堂小结
线段的性质:两点之间,线段最短.
两点的距离:连接两点间的线段的长度,叫做这两点的距离.
1、如图,点C在线段AB上,点D是AC的中点,如果BC= CD,AB=7 cm,求BC的长.
提高练习
2、如图,M、N是线段EF上两点,已知 EA : AB: BF =1:2:3,M、N分别为EA、BF的中点,且MN=8,求EF的长.
E
A
B
N
F
M
x
x
4x
6x
8
3x
提高练习
3、已知线段AB=10,点C在直线AB上,且AC=4,若点D是AB的中点,求DC的长.
情况一:点C在A的左侧
情况二:点C在A的右侧
提高练习
