人教版数学七年级上册 1.2有理数复习课 课件(共25张PPT)
文档属性
| 名称 | 人教版数学七年级上册 1.2有理数复习课 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 451.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-15 10:47:06 | ||
图片预览







文档简介
(共25张PPT)
复习课
第一章 有理数
学习目标
1.梳理有理数的有关概念,理解概念之间的内在联系;
2.熟练地进行有理数的运算,并能运用运算律简化运算,体会数系扩充之后运算的一致性;
3.通过利用数轴的直观性解决问题,体会数形结合的思想方法.
一、知识回顾
一、有理数的基本概念
1.有理数.
2.数轴.
3.互为相反数.
4.有理数的绝对值.
5.互为倒数.
6.有理数的乘方.
7.科学记数法、近似数与精确度.
二、有理数的运算
加、减、乘、除、乘方的混合运算.
二、知识要点
1.负数:
在正数前面加“-”的数.
0既不是正数,也不是负数.
判断:(1)a一定是正数; (2)-a一定是负数;
(3)-(-a)一定大于0; (4)0是正整数.
×
×
×
×
(1)带“-”号的数都是负数; (2)0℃表示没有温度;
(3)不存在既不是正数,也不是负数的数;
(4)增加-20%,实际的意思是 .
甲比乙大-3表示的意思是 .
练习
二、知识要点
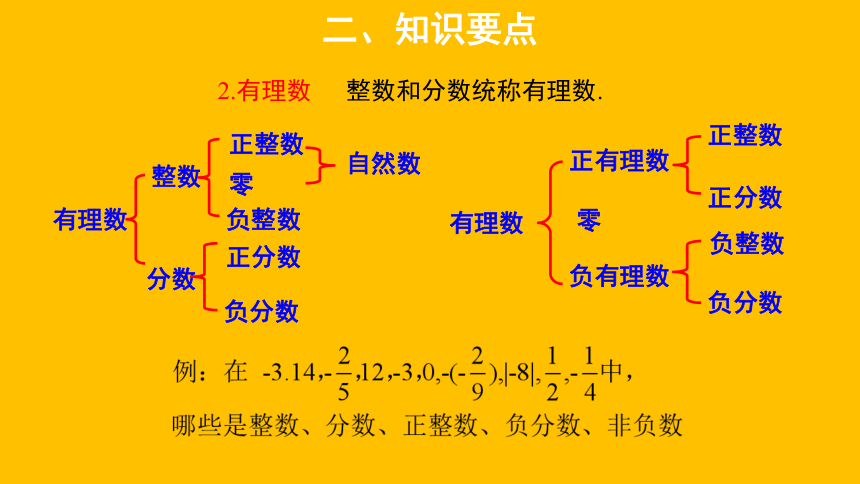
整数和分数统称有理数.
有理数
整数
分数
正整数
零
负整数
自然数
正分数
负分数
有理数
正有理数
零
负有理数
正整数
正分数
负整数
负分数
2.有理数
二、知识要点
3.数轴
规定了原点、正方向和单位长度的直线.
–3 –2 –1 0 1 2 3 4
(1)在数轴上表示的两个数,右边的数总比左边的数大;
(2)正数都大于0,负数都小于0;正数大于一切负数;
(3)所有有理数都可以用数轴上的点表示.
练习:在数轴上画出表示下列各数的点,并按从大到小的顺序排列,用“>”号连接起来. 4,-|-2|,-4.5,1,0.
二、知识要点
只有符号不同的两个数,其中一个是另一个的相反数.
4.相反数
(1)数a的相反数是-a
(a是任意一个有理数);
(2) 0的相反数是0.
(3)若a、b互为相反数,则a+b=0.
练习:(1)如果a=-13,那么-a=______;
(2)如果-a=-5.4,那么a=______;
(3)如果-x=-6,那么x=______;
(4)-x=9,那么x=______.
二、知识要点
5.倒数
乘积是1的两个数互为倒数.
(1) a的倒数是 (a≠0);
(2) 0没有倒数;
(3)若a与b互为倒数,则ab=1;
(4)倒数是它本身的是______.
练习:下列各数,哪两个数互为倒数?
8, ,-1,+(-8), ,1.
二、知识要点
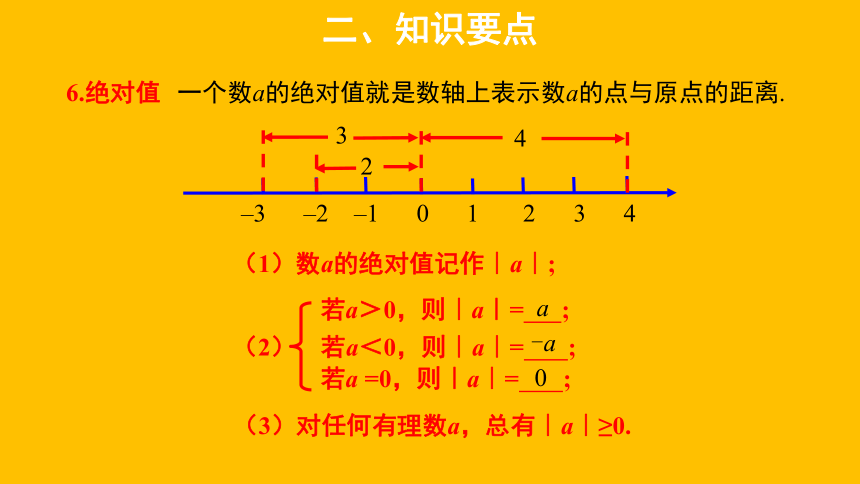
6.绝对值
一个数a的绝对值就是数轴上表示数a的点与原点的距离.
–3 –2 –1 0 1 2 3 4
2
3
4
(1)数a的绝对值记作︱a︱;
若a>0,则︱a︱= ;
(2) 若a<0,则︱a︱= ;
若a =0,则︱a︱= ;
a
-a
0
(3)对任何有理数a,总有︱a︱≥0.
二、知识要点
7.有理数大小的比较
(1)可通过数轴比较:
在数轴上的两个数,右边的数总比左边的数大;
正数都大于0,负数都小于0;正数大于一切负数;
(2)两个负数,绝对值大的反而小.
即:若a<0,b<0,且︱a︱>︱b︱,则a < b.
8.科学记数法、近似数
把一个大于10的数记成a×10n的形式,其中a是整数位只有一位的数,这种记数法叫做科学记数法 .
二、知识要点
有理数的运算
减法
加法
乘法
除法
乘方
转化
转化
交换律
结合律
有理数的混合运算
1.有括号,先算括号里面的;
2.先算乘方,再算乘除,最 后算加减;
3.对只含乘除,或只含加减的运算,应从左往右运算.
三、巩固练习
计算:
(1)
(2)
(3)
(4)
三、巩固练习
把减法转化为加法时,要注意减号和减数的性质符号要同时改变.对多个有理数相加减的题目,要观察数的特征,能利用运算律时,要利用运算律使计算简便 .
三、巩固练习
运用运算律时要注意符号问题.
三、巩固练习
运用除法法则进行运算时,首先应确定商的符号,然后把绝对值相除,还要注意,对同一级运算要按从左至右的顺序进行.
三、巩固练习
三、巩固练习
计算下列各式:
-22 -(-2)2 - 23 +(-2)3
(-1)2n+(-1)2n+1= (n是正整数)
四、典例精析
例1 观察下列五组数:1,-1,-1;
2,-4,-6;
3,-9,-15;
4,-16,-28;
5,-25,-45;
…
(1)每组数中的第2个数与第1个数有什么关系?
(2)每组数中的第3个数与第1个数有什么关系?
(3)计算第50组数的和.
四、典例精析
解:(1)每组数中的第2个数分别是:
每组数中的第2个数是第1个数的平方的相反数;
每组数中的第3个数是第1个数乘第1个数的2倍与1的差所得积的相反数;
(2)每组数中的第3个数分别是:
, , , , ,…,
即, , ,
, ,… .
四、典例精析
(3)第50组数的3个数分别是50, ,
,它们的和为:
【问题】怎样解决有关数的规律探索性问题(结合例1)?
1.对每组中的数从符号、绝对值两方面考虑.
2.把数的绝对值与组数的序号联系起来.
四、典例精析
例2 结合具体的数的运算,归纳有关特例,然后比较下列数的大小:
(1)小于1的正数 , 的平方, 的立方;
(2)大于-1的负数 , 的平方, 的立方.
四、典例精析
解:由 , , ,
根据有理数加法法则,得 .
在数轴上画出表示 、 、 、 的点,
-b
-a
b
a
0
由上图,得 .
四、典例精析
【问题】在例2、例3的学习过程中,你有什么体会?
例2:是通过具体计算,归纳得出结论,体会由特殊到一般这一认识事物规律的方法.
例3:是通过把表示 、 、 、 的点在数轴上表示出来,即利用数轴解决问题,体会数形结合的方法.
五、课堂小结
谈一谈你的收获与体会!
● 注重分类讨论的思想.
● 注重应用转化的思想.
● 注重数形结合的思想.
再 见
复习课
第一章 有理数
学习目标
1.梳理有理数的有关概念,理解概念之间的内在联系;
2.熟练地进行有理数的运算,并能运用运算律简化运算,体会数系扩充之后运算的一致性;
3.通过利用数轴的直观性解决问题,体会数形结合的思想方法.
一、知识回顾
一、有理数的基本概念
1.有理数.
2.数轴.
3.互为相反数.
4.有理数的绝对值.
5.互为倒数.
6.有理数的乘方.
7.科学记数法、近似数与精确度.
二、有理数的运算
加、减、乘、除、乘方的混合运算.
二、知识要点
1.负数:
在正数前面加“-”的数.
0既不是正数,也不是负数.
判断:(1)a一定是正数; (2)-a一定是负数;
(3)-(-a)一定大于0; (4)0是正整数.
×
×
×
×
(1)带“-”号的数都是负数; (2)0℃表示没有温度;
(3)不存在既不是正数,也不是负数的数;
(4)增加-20%,实际的意思是 .
甲比乙大-3表示的意思是 .
练习
二、知识要点
整数和分数统称有理数.
有理数
整数
分数
正整数
零
负整数
自然数
正分数
负分数
有理数
正有理数
零
负有理数
正整数
正分数
负整数
负分数
2.有理数
二、知识要点
3.数轴
规定了原点、正方向和单位长度的直线.
–3 –2 –1 0 1 2 3 4
(1)在数轴上表示的两个数,右边的数总比左边的数大;
(2)正数都大于0,负数都小于0;正数大于一切负数;
(3)所有有理数都可以用数轴上的点表示.
练习:在数轴上画出表示下列各数的点,并按从大到小的顺序排列,用“>”号连接起来. 4,-|-2|,-4.5,1,0.
二、知识要点
只有符号不同的两个数,其中一个是另一个的相反数.
4.相反数
(1)数a的相反数是-a
(a是任意一个有理数);
(2) 0的相反数是0.
(3)若a、b互为相反数,则a+b=0.
练习:(1)如果a=-13,那么-a=______;
(2)如果-a=-5.4,那么a=______;
(3)如果-x=-6,那么x=______;
(4)-x=9,那么x=______.
二、知识要点
5.倒数
乘积是1的两个数互为倒数.
(1) a的倒数是 (a≠0);
(2) 0没有倒数;
(3)若a与b互为倒数,则ab=1;
(4)倒数是它本身的是______.
练习:下列各数,哪两个数互为倒数?
8, ,-1,+(-8), ,1.
二、知识要点
6.绝对值
一个数a的绝对值就是数轴上表示数a的点与原点的距离.
–3 –2 –1 0 1 2 3 4
2
3
4
(1)数a的绝对值记作︱a︱;
若a>0,则︱a︱= ;
(2) 若a<0,则︱a︱= ;
若a =0,则︱a︱= ;
a
-a
0
(3)对任何有理数a,总有︱a︱≥0.
二、知识要点
7.有理数大小的比较
(1)可通过数轴比较:
在数轴上的两个数,右边的数总比左边的数大;
正数都大于0,负数都小于0;正数大于一切负数;
(2)两个负数,绝对值大的反而小.
即:若a<0,b<0,且︱a︱>︱b︱,则a < b.
8.科学记数法、近似数
把一个大于10的数记成a×10n的形式,其中a是整数位只有一位的数,这种记数法叫做科学记数法 .
二、知识要点
有理数的运算
减法
加法
乘法
除法
乘方
转化
转化
交换律
结合律
有理数的混合运算
1.有括号,先算括号里面的;
2.先算乘方,再算乘除,最 后算加减;
3.对只含乘除,或只含加减的运算,应从左往右运算.
三、巩固练习
计算:
(1)
(2)
(3)
(4)
三、巩固练习
把减法转化为加法时,要注意减号和减数的性质符号要同时改变.对多个有理数相加减的题目,要观察数的特征,能利用运算律时,要利用运算律使计算简便 .
三、巩固练习
运用运算律时要注意符号问题.
三、巩固练习
运用除法法则进行运算时,首先应确定商的符号,然后把绝对值相除,还要注意,对同一级运算要按从左至右的顺序进行.
三、巩固练习
三、巩固练习
计算下列各式:
-22 -(-2)2 - 23 +(-2)3
(-1)2n+(-1)2n+1= (n是正整数)
四、典例精析
例1 观察下列五组数:1,-1,-1;
2,-4,-6;
3,-9,-15;
4,-16,-28;
5,-25,-45;
…
(1)每组数中的第2个数与第1个数有什么关系?
(2)每组数中的第3个数与第1个数有什么关系?
(3)计算第50组数的和.
四、典例精析
解:(1)每组数中的第2个数分别是:
每组数中的第2个数是第1个数的平方的相反数;
每组数中的第3个数是第1个数乘第1个数的2倍与1的差所得积的相反数;
(2)每组数中的第3个数分别是:
, , , , ,…,
即, , ,
, ,… .
四、典例精析
(3)第50组数的3个数分别是50, ,
,它们的和为:
【问题】怎样解决有关数的规律探索性问题(结合例1)?
1.对每组中的数从符号、绝对值两方面考虑.
2.把数的绝对值与组数的序号联系起来.
四、典例精析
例2 结合具体的数的运算,归纳有关特例,然后比较下列数的大小:
(1)小于1的正数 , 的平方, 的立方;
(2)大于-1的负数 , 的平方, 的立方.
四、典例精析
解:由 , , ,
根据有理数加法法则,得 .
在数轴上画出表示 、 、 、 的点,
-b
-a
b
a
0
由上图,得 .
四、典例精析
【问题】在例2、例3的学习过程中,你有什么体会?
例2:是通过具体计算,归纳得出结论,体会由特殊到一般这一认识事物规律的方法.
例3:是通过把表示 、 、 、 的点在数轴上表示出来,即利用数轴解决问题,体会数形结合的方法.
五、课堂小结
谈一谈你的收获与体会!
● 注重分类讨论的思想.
● 注重应用转化的思想.
● 注重数形结合的思想.
再 见
