人教版数学七年级上册 2.1整式(1)课件(共16张PPT)
文档属性
| 名称 | 人教版数学七年级上册 2.1整式(1)课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-15 11:02:01 | ||
图片预览





文档简介
(共16张PPT)
第二章 整式的加减
2.1 整式
第 1 课时
一、创设情境,引入新知
【问题1】
青藏铁路线上,在格尔木到拉萨之间有一段很长的冻土地段.列车在冻土地段的行驶速度是100 km/h.列车在冻土地段行驶时,根据已知数据求出列车行驶的路程.
(1)2 h 行驶多少千米?3 h 呢?8 h 呢?t h呢?
(2)字母 t 表示时间有什么意义
如果用 v 表示速度,列车行驶的路程是多少?
(3)回顾以前所学的知识,你还能举出用字母表示
数或数量关系的例子吗?
一、创设情境,引入新知
【问题2】
怎样分析数量关系并用含有字母的式子表示数量关系呢?
例1
(1)苹果原价是每千克 p 元,按 8 折优惠出售,用式子表示现价;
(2)某产品前年的产量是 n 件,去年的产量是前年产量的 m 倍,用式子表示去年的产量;
(3)一个长方体包装盒的长和宽都是 a cm,高是 h cm,用式子表示它的体积;
(4)用式子表示数 n 的相反数.
答案:(1) ;(2) ;(3) ;(4) .
二、合作交流,探究新知
例2
(1)一条河的水流速度是 2.5 km/h,船在静水中的速度是 v km/h,用式子表示船在这条河中顺水行驶和逆水行驶时的速度;
(2)买一个篮球需要 x 元,买一个排球需要y元,买一个足球需要 z 元,用式子表示买 3个篮球、5个排球、2 个足球共需要的钱数;
二、合作交流,探究新知
解:
(1)船在这条河中顺水行驶的速度是 km/h,
逆水行驶的速度是 km/h.
(2)买 3 个篮球、5 个排球、2 个足球共需要 元.
例2
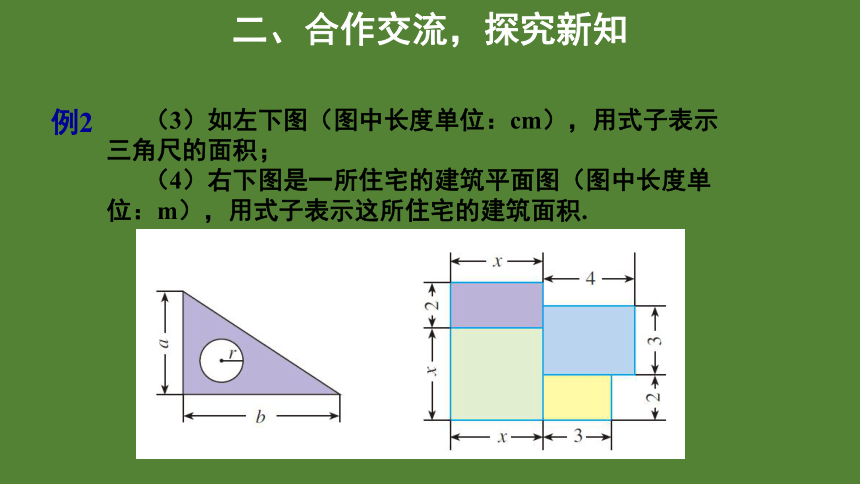
(3)如左下图(图中长度单位:cm),用式子表示三角尺的面积;
(4)右下图是一所住宅的建筑平面图(图中长度单位:m),用式子表示这所住宅的建筑面积.
二、合作交流,探究新知
(3)三角尺的面积(单位:cm2 )是 .
(4)这所住宅的建筑面积(单位:m2)是 .
归纳:
列式就是把实际问题中与数量有关的语句,用含有数、字母和运算符号的式子表示出来,也就是把文字语言转化为符号语言.
二、合作交流,探究新知
列式时:
①要抓住关键词语,明确它们的意义以及它们 之间的关系,如和、差、积、商及大、小、多、少、倍、分、倒数、相反数等;
②理清语句层次明确运算顺序;
③牢记一些概念和公式.
二、合作交流,探究新知
列式时:
①数与字母、字母与字母相乘省略乘号;
②数与字母相乘时数字在前;
③式子中出现除法运算时,一般按分数形式来写;
④带分数与字母相乘时,把带分数化成假分数;
⑤带单位时,适当加括号.
二、合作交流,探究新知
1.
(1)观察下列各式: , , , ,… ,按此规律,第 个式子是 ;
(2)测得一种树苗的高度与树苗生长的年数的有关数据如下表(树苗原高 100 cm),根据表格思考下面问题:
年数 高度/cm
1 100+5
2 100+10
3 100+15
4 100+20
…… ……
前四年树苗高度的变化与年数有什么关系?假设以后各年树苗高度的变化与年数保持上述关系,用式子表示生长了 n 年的树苗的高度.
100+5×1
100+5×3
100+5×2
100+5×4
100+5×n
……
三、运用新知
(3)礼堂第 1 排有 20 个座位,后面每排都比前一排多一个座位.用式子表示第 n 排的座位数.
用整式表示实际问题中的数量关系和变化规律,可以从特殊值入手,借助表格等分析,由特殊到一般,由个体到整体地观察、分析问题,发现规律,并用含有字母的式子表示一般的结论,这体现了抽象的数学思想.
三、运用新知
1.
(1)某种商品每袋4.8元,在一个月内的销售量是 m 袋,用
式子表示在这个月内销售这种商品的收入.
(2)圆柱体的底面半径、高分别是 r,h,用式子表示圆柱体
的体积.
(3)有两片棉田,一片有m hm2 (公顷,1 hm2 =104 m2 ),平
均每公顷产棉花a kg;另一片有n hm2 ,平均每公顷产棉
花b kg,用式子表示两片棉田上棉花的总产量.
(4)在一个大正方形铁片中挖去一个小正方形铁片,大正方
形的边长是a mm,小正方形的边长是b mm,用式子表示
剩余部分的面积.
四、巩固新知
(1)5 箱苹果重 m kg,每箱重 kg ;
(2)一个数比 a 的 2 倍小 5,则这个数为 ;
(3)全校学生总数是 x,其中女生占总数52%,则女生人数是 ,
男生人数是 ;
(4)某校前年购买计算机 x 台,去年购买数量是前年的 2 倍,今年购
买数量又是去年的2倍,则学校三年共购买计算机 台;
(5)某班有 a 名学生,现把一批图书分给全班学生阅读,如果每人分
4本,还缺 25 本,则这批图书共 本;
(6)一个两位数,十位上的数字为 a,个位上的数字为 b,则这个两位
数为 .
2.
四、巩固新知
列式时:
①数与字母、字母与字母相乘省略乘号;
②数与字母相乘时数字在前;
③式子中出现除法运算时,一般按分数形式来写;
④带分数与字母相乘时,把带分数化成假分数;
⑤带单位时,适当加括号.
五、归纳小结
科学家爱因斯坦在谈成功的秘诀时,写下了一个公式:A=X+Y+Z,
他解释道:A代表成功,
X代表艰苦的劳动,
Y代表正确的方法,
Z代表少说空话.
共勉
五、归纳小结
再 见
第二章 整式的加减
2.1 整式
第 1 课时
一、创设情境,引入新知
【问题1】
青藏铁路线上,在格尔木到拉萨之间有一段很长的冻土地段.列车在冻土地段的行驶速度是100 km/h.列车在冻土地段行驶时,根据已知数据求出列车行驶的路程.
(1)2 h 行驶多少千米?3 h 呢?8 h 呢?t h呢?
(2)字母 t 表示时间有什么意义
如果用 v 表示速度,列车行驶的路程是多少?
(3)回顾以前所学的知识,你还能举出用字母表示
数或数量关系的例子吗?
一、创设情境,引入新知
【问题2】
怎样分析数量关系并用含有字母的式子表示数量关系呢?
例1
(1)苹果原价是每千克 p 元,按 8 折优惠出售,用式子表示现价;
(2)某产品前年的产量是 n 件,去年的产量是前年产量的 m 倍,用式子表示去年的产量;
(3)一个长方体包装盒的长和宽都是 a cm,高是 h cm,用式子表示它的体积;
(4)用式子表示数 n 的相反数.
答案:(1) ;(2) ;(3) ;(4) .
二、合作交流,探究新知
例2
(1)一条河的水流速度是 2.5 km/h,船在静水中的速度是 v km/h,用式子表示船在这条河中顺水行驶和逆水行驶时的速度;
(2)买一个篮球需要 x 元,买一个排球需要y元,买一个足球需要 z 元,用式子表示买 3个篮球、5个排球、2 个足球共需要的钱数;
二、合作交流,探究新知
解:
(1)船在这条河中顺水行驶的速度是 km/h,
逆水行驶的速度是 km/h.
(2)买 3 个篮球、5 个排球、2 个足球共需要 元.
例2
(3)如左下图(图中长度单位:cm),用式子表示三角尺的面积;
(4)右下图是一所住宅的建筑平面图(图中长度单位:m),用式子表示这所住宅的建筑面积.
二、合作交流,探究新知
(3)三角尺的面积(单位:cm2 )是 .
(4)这所住宅的建筑面积(单位:m2)是 .
归纳:
列式就是把实际问题中与数量有关的语句,用含有数、字母和运算符号的式子表示出来,也就是把文字语言转化为符号语言.
二、合作交流,探究新知
列式时:
①要抓住关键词语,明确它们的意义以及它们 之间的关系,如和、差、积、商及大、小、多、少、倍、分、倒数、相反数等;
②理清语句层次明确运算顺序;
③牢记一些概念和公式.
二、合作交流,探究新知
列式时:
①数与字母、字母与字母相乘省略乘号;
②数与字母相乘时数字在前;
③式子中出现除法运算时,一般按分数形式来写;
④带分数与字母相乘时,把带分数化成假分数;
⑤带单位时,适当加括号.
二、合作交流,探究新知
1.
(1)观察下列各式: , , , ,… ,按此规律,第 个式子是 ;
(2)测得一种树苗的高度与树苗生长的年数的有关数据如下表(树苗原高 100 cm),根据表格思考下面问题:
年数 高度/cm
1 100+5
2 100+10
3 100+15
4 100+20
…… ……
前四年树苗高度的变化与年数有什么关系?假设以后各年树苗高度的变化与年数保持上述关系,用式子表示生长了 n 年的树苗的高度.
100+5×1
100+5×3
100+5×2
100+5×4
100+5×n
……
三、运用新知
(3)礼堂第 1 排有 20 个座位,后面每排都比前一排多一个座位.用式子表示第 n 排的座位数.
用整式表示实际问题中的数量关系和变化规律,可以从特殊值入手,借助表格等分析,由特殊到一般,由个体到整体地观察、分析问题,发现规律,并用含有字母的式子表示一般的结论,这体现了抽象的数学思想.
三、运用新知
1.
(1)某种商品每袋4.8元,在一个月内的销售量是 m 袋,用
式子表示在这个月内销售这种商品的收入.
(2)圆柱体的底面半径、高分别是 r,h,用式子表示圆柱体
的体积.
(3)有两片棉田,一片有m hm2 (公顷,1 hm2 =104 m2 ),平
均每公顷产棉花a kg;另一片有n hm2 ,平均每公顷产棉
花b kg,用式子表示两片棉田上棉花的总产量.
(4)在一个大正方形铁片中挖去一个小正方形铁片,大正方
形的边长是a mm,小正方形的边长是b mm,用式子表示
剩余部分的面积.
四、巩固新知
(1)5 箱苹果重 m kg,每箱重 kg ;
(2)一个数比 a 的 2 倍小 5,则这个数为 ;
(3)全校学生总数是 x,其中女生占总数52%,则女生人数是 ,
男生人数是 ;
(4)某校前年购买计算机 x 台,去年购买数量是前年的 2 倍,今年购
买数量又是去年的2倍,则学校三年共购买计算机 台;
(5)某班有 a 名学生,现把一批图书分给全班学生阅读,如果每人分
4本,还缺 25 本,则这批图书共 本;
(6)一个两位数,十位上的数字为 a,个位上的数字为 b,则这个两位
数为 .
2.
四、巩固新知
列式时:
①数与字母、字母与字母相乘省略乘号;
②数与字母相乘时数字在前;
③式子中出现除法运算时,一般按分数形式来写;
④带分数与字母相乘时,把带分数化成假分数;
⑤带单位时,适当加括号.
五、归纳小结
科学家爱因斯坦在谈成功的秘诀时,写下了一个公式:A=X+Y+Z,
他解释道:A代表成功,
X代表艰苦的劳动,
Y代表正确的方法,
Z代表少说空话.
共勉
五、归纳小结
再 见
