人教版数学七年级下册5.3.1 平行线的性质 课件(共23张ppt)
文档属性
| 名称 | 人教版数学七年级下册5.3.1 平行线的性质 课件(共23张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 220.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-15 12:43:56 | ||
图片预览








文档简介
(共23张PPT)
第五章 相交线与平行线
5.3 平行线的性质
第1课时 平行线的性质
1.理解平行线的性质和判定的区别.
2.掌握平行线的三个性质,并能运用它们作简单的推理.
学习目标
复习回顾
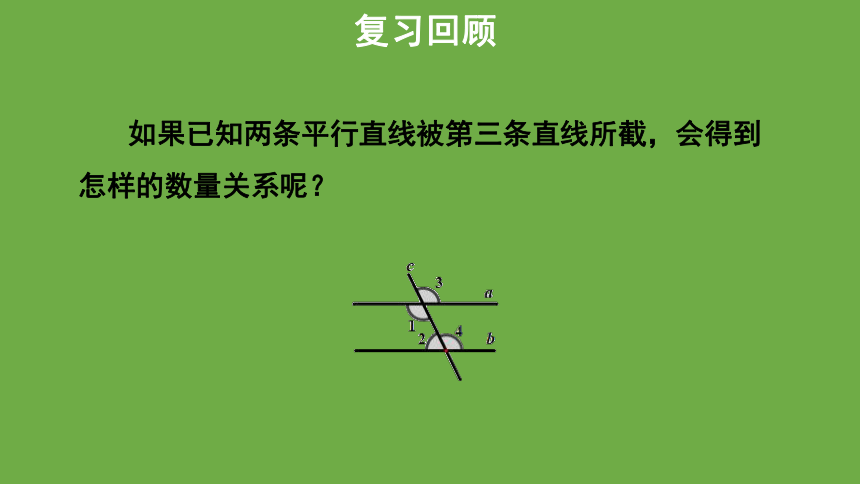
如果已知两条平行直线被第三条直线所截,会得到怎样的数量关系呢?
复习回顾
思考:
猜想1:两条平行直线被三条直线所截,同位角相等;
猜想2:两条平行直线被三条直线所截,内错角相等;
猜想3:两条平行直线被三条直线所截,同旁内角互补;
新知讲解
平行线的性质
①设l1//l2,l3与它们相交,度量∠1和∠2的大小,你能发现什么关系?
∠1=∠2
新知讲解
平行线的性质
②如图,直线l4,度量一下∠3和∠4的大小,你还能发现它们有什么关系?
∠3=∠4
新知讲解
平行线的性质1:
两条平行线被第三条直线所截,同位角相等。
简称:两直线平行,同位角相等。
新知讲解
如图,已知a∥b,直线a,b被直线c所截。求证:∠2=∠3。
证明:
∵a∥b,
∴∠1=∠2(两直线平行,同位角相等)
∵∠1=∠3(对顶角相等)
∴∠2=∠3(等量代换)
新知讲解
平行线的性质2:
两条平行线被第三条直线所截,内错角相等。
简称:两直线平行,内错角相等。
新知讲解
如图,已知a∥b,直线a,b被直线c所截。说明:∠2+∠3=180°。
解:
∵a∥b,
∴∠1=∠2(两直线平行,同位角相等)
∵∠1+∠3=180°(互补)
∴∠2+∠3=180°(等量代换)
新知讲解
平行线的性质3:
两条平行线被第三条直线所截,同旁内角互补。
简称:两直线平行,同旁内角互补。
新知讲解
平行线判定与性质的区别与联系
性质:根据两条直线平行,去证明角的相等或互补。
判定:根据两角相等或互补,去证明两条直线平行。
典型例题
例1:如图,直线a,b被直线c所截,下列说法正确的是( )
A.当∠1=∠2时,则有a∥b
B.当a∥b时,则有∠1=∠2
C.当a∥b时,则有∠1+∠2=180°
D.当a∥b时,则有∠1+∠2=90°
典型例题
解析:如图:
A.∵∠2与∠3互为邻补角,∴∠3=180°-∠2.
当∠1=∠2,即∠3=180°-∠1,无法得到a∥b,故错误;
B.当a∥b时,根据两直线平行,同位角相等,一定有∠1=∠3。∵∠2与∠3互为邻补角∴∠3+∠2=180°,即∠1+∠2=180°,故错误;
典型例题
解析:如图:
C.由B知,该项正确;
D.由B知,该项错误。
所以选C。
典型例题
例2:如图,AB∥CD,EF⊥DB,垂足为E,∠1=50°,则∠2的大小为 。
分析:∵AB∥CD,∴∠2=∠D,
又∵EF⊥DB,∠1=50°,
∴∠D=90°-∠1=40°,
即∠2=40°。 ∴∠2的大小为40°
40°
典型例题
例3:将直尺和三角板按如图方式放置,已知∠1=30°,则∠2的大小为 。
分析:∵AB∥CD,∴∠2=∠3
又∵∠3+∠1=90°,∠1=30°,
∴∠3=90°-∠1=60°,∴∠2=60°
所以∠2的度数为60°。
60°
随堂练习
1. 下列四个图形中,不能推出∠2与∠1相等的是( )
A.
B.
D.
C.
B
随堂练习
2. 下列说法:
①两直线平行,同旁内角互补;②同位角相等,两直线平行;③内错角相等,两直线平行;④两直线平行,同位角相等.
其中是平行线特征的是( )
D
A.① B. ②③ C.④ D.①④
随堂练习
3. 如图,∠1+∠B=180°,∠2=45°,则∠D的度数是( )。
A.25°
B.45°
C.50°
D.65°
B
随堂练习
4. 如图,直线AB,CD被直线EF所截交于点M和点N,MP平分∠BMN,NP平分∠DNM,若∠BMN+∠DNM=180°,则∠1+∠2=________ .
90°
平行线的性质:
两直线平行,同位角相等。
两直线平行,内错角相等。
两直线平行,同旁内角互补。
课堂小结
再 见
第五章 相交线与平行线
5.3 平行线的性质
第1课时 平行线的性质
1.理解平行线的性质和判定的区别.
2.掌握平行线的三个性质,并能运用它们作简单的推理.
学习目标
复习回顾
如果已知两条平行直线被第三条直线所截,会得到怎样的数量关系呢?
复习回顾
思考:
猜想1:两条平行直线被三条直线所截,同位角相等;
猜想2:两条平行直线被三条直线所截,内错角相等;
猜想3:两条平行直线被三条直线所截,同旁内角互补;
新知讲解
平行线的性质
①设l1//l2,l3与它们相交,度量∠1和∠2的大小,你能发现什么关系?
∠1=∠2
新知讲解
平行线的性质
②如图,直线l4,度量一下∠3和∠4的大小,你还能发现它们有什么关系?
∠3=∠4
新知讲解
平行线的性质1:
两条平行线被第三条直线所截,同位角相等。
简称:两直线平行,同位角相等。
新知讲解
如图,已知a∥b,直线a,b被直线c所截。求证:∠2=∠3。
证明:
∵a∥b,
∴∠1=∠2(两直线平行,同位角相等)
∵∠1=∠3(对顶角相等)
∴∠2=∠3(等量代换)
新知讲解
平行线的性质2:
两条平行线被第三条直线所截,内错角相等。
简称:两直线平行,内错角相等。
新知讲解
如图,已知a∥b,直线a,b被直线c所截。说明:∠2+∠3=180°。
解:
∵a∥b,
∴∠1=∠2(两直线平行,同位角相等)
∵∠1+∠3=180°(互补)
∴∠2+∠3=180°(等量代换)
新知讲解
平行线的性质3:
两条平行线被第三条直线所截,同旁内角互补。
简称:两直线平行,同旁内角互补。
新知讲解
平行线判定与性质的区别与联系
性质:根据两条直线平行,去证明角的相等或互补。
判定:根据两角相等或互补,去证明两条直线平行。
典型例题
例1:如图,直线a,b被直线c所截,下列说法正确的是( )
A.当∠1=∠2时,则有a∥b
B.当a∥b时,则有∠1=∠2
C.当a∥b时,则有∠1+∠2=180°
D.当a∥b时,则有∠1+∠2=90°
典型例题
解析:如图:
A.∵∠2与∠3互为邻补角,∴∠3=180°-∠2.
当∠1=∠2,即∠3=180°-∠1,无法得到a∥b,故错误;
B.当a∥b时,根据两直线平行,同位角相等,一定有∠1=∠3。∵∠2与∠3互为邻补角∴∠3+∠2=180°,即∠1+∠2=180°,故错误;
典型例题
解析:如图:
C.由B知,该项正确;
D.由B知,该项错误。
所以选C。
典型例题
例2:如图,AB∥CD,EF⊥DB,垂足为E,∠1=50°,则∠2的大小为 。
分析:∵AB∥CD,∴∠2=∠D,
又∵EF⊥DB,∠1=50°,
∴∠D=90°-∠1=40°,
即∠2=40°。 ∴∠2的大小为40°
40°
典型例题
例3:将直尺和三角板按如图方式放置,已知∠1=30°,则∠2的大小为 。
分析:∵AB∥CD,∴∠2=∠3
又∵∠3+∠1=90°,∠1=30°,
∴∠3=90°-∠1=60°,∴∠2=60°
所以∠2的度数为60°。
60°
随堂练习
1. 下列四个图形中,不能推出∠2与∠1相等的是( )
A.
B.
D.
C.
B
随堂练习
2. 下列说法:
①两直线平行,同旁内角互补;②同位角相等,两直线平行;③内错角相等,两直线平行;④两直线平行,同位角相等.
其中是平行线特征的是( )
D
A.① B. ②③ C.④ D.①④
随堂练习
3. 如图,∠1+∠B=180°,∠2=45°,则∠D的度数是( )。
A.25°
B.45°
C.50°
D.65°
B
随堂练习
4. 如图,直线AB,CD被直线EF所截交于点M和点N,MP平分∠BMN,NP平分∠DNM,若∠BMN+∠DNM=180°,则∠1+∠2=________ .
90°
平行线的性质:
两直线平行,同位角相等。
两直线平行,内错角相等。
两直线平行,同旁内角互补。
课堂小结
再 见
