人教版数学七年级下册6.1 算术平方根 课件(共18张ppt)
文档属性
| 名称 | 人教版数学七年级下册6.1 算术平方根 课件(共18张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 524.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-15 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
第六章 实数
6.1 平方根
第1课时 算术平方根
1.经历算术平方根概念的形成过程,了解算术平方根的概念.
2.会求某些正数(完全平方数)的算术平方根并会用符号表示.
学习目标
新知讲解
算术平方根
学校要举行美术作品比赛,小鸥想裁出一块面积为25 dm2的正方形画布,画上自己的得意之作参加比赛,这块正方形画布的边长应取多少?
(1)这块正方形画布的边长应取多少厘米?你是怎么算出来的?
答:5 dm,因为52=25。
(2)完成下表
正方形的面积/dm2 1 9 16 36
正方形的边长/dm
1
3
4
6
(3)你能指出它们的共同特点吗?
都是已知一个正数的平方,求这个正数.
新知讲解
算术平方根
正数3的平方等于9,我们把正数3叫做9的算术平方根.
正数4的平方等于16,我们把正数4叫做16的算术平方根.
如果一个正数的平方等于a,那么这个正数叫做a的算术平方根.
为了书写方便,我们把a的算术平方根记作 .
新知讲解
算术平方根
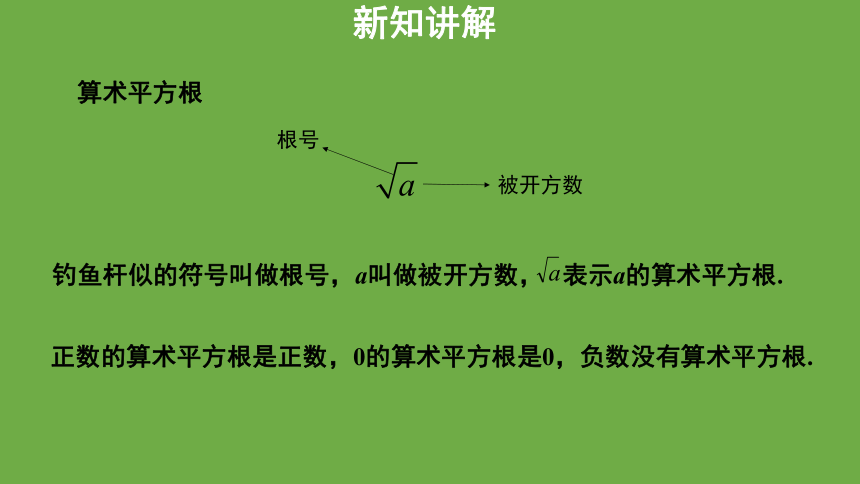
钓鱼杆似的符号叫做根号,a叫做被开方数, 表示a的算术平方根.
正数的算术平方根是正数,0的算术平方根是0,负数没有算术平方根.
新知讲解
根号
被开方数
思考:你知道 有多大吗
因为
所以
因为
所以
新知讲解
如此进行下去,可以得到 的更精确的近似值.
事实上, ,它是 一个无限不循环小数.
利用计算器计算,我们会发现 都是无限不循环小数.
新知讲解
怎样求 的近似值。
新知讲解
算术平方根小数点移动法则
规律:被开方数的小数点每向右(或向左)移动两位,它的算术平方根的小数点就向右(或向左)移动一位.
新知讲解
典型例题
例1:求下列各数的算术平方根.
(1)
(2)
0.0001
(1)因为( )2= ,
所以 的算术平方根为 .
(2)因为(0.01)2=0.0001,
所以0.0001的算术平方根是0.01.
例2:估算 在哪两个整数之间?
解:
∵被求式是在两个整数之间,
典型例题
例3:已知 ≈2.284, ≈7.232,则
(1) ≈ 。
(2)若 ≈0.02284,则x= 。
分析:(1) 向左移动四位就是 ,所以7.232应向左移动两位为0.07232。
(2)2.284向左移动两位为0.02284,所以 需要向左移动四位为 。
0.07232
典型例题
随堂练习
1 .用计算器求下列各式的值。
(1) (精确到0.001)
解:(1)1.732 (2)56.000
(2)
2 .算术平方根等于它本身的数是______;______的算术平方根等于它的相反数。
0和1
0
3 .已知9的算术平方根为a,b的绝对值为4,则a-b的值为________.
-1或7
随堂练习
4 .求下列各数的算术平方根。
(1)(-3)2
(2)
(3)0
(4)
3
0
3
随堂练习
课堂小结
如果一个正数的平方等于a,那么这个正数叫做a的算术平方根.
把a的算术平方根记作 .
a叫做被开方数, 表示a的算术平方根.
注:正数的算术平方根是正数,
0的算术平方根是0,
负数没有算术平方根.
再见
第六章 实数
6.1 平方根
第1课时 算术平方根
1.经历算术平方根概念的形成过程,了解算术平方根的概念.
2.会求某些正数(完全平方数)的算术平方根并会用符号表示.
学习目标
新知讲解
算术平方根
学校要举行美术作品比赛,小鸥想裁出一块面积为25 dm2的正方形画布,画上自己的得意之作参加比赛,这块正方形画布的边长应取多少?
(1)这块正方形画布的边长应取多少厘米?你是怎么算出来的?
答:5 dm,因为52=25。
(2)完成下表
正方形的面积/dm2 1 9 16 36
正方形的边长/dm
1
3
4
6
(3)你能指出它们的共同特点吗?
都是已知一个正数的平方,求这个正数.
新知讲解
算术平方根
正数3的平方等于9,我们把正数3叫做9的算术平方根.
正数4的平方等于16,我们把正数4叫做16的算术平方根.
如果一个正数的平方等于a,那么这个正数叫做a的算术平方根.
为了书写方便,我们把a的算术平方根记作 .
新知讲解
算术平方根
钓鱼杆似的符号叫做根号,a叫做被开方数, 表示a的算术平方根.
正数的算术平方根是正数,0的算术平方根是0,负数没有算术平方根.
新知讲解
根号
被开方数
思考:你知道 有多大吗
因为
所以
因为
所以
新知讲解
如此进行下去,可以得到 的更精确的近似值.
事实上, ,它是 一个无限不循环小数.
利用计算器计算,我们会发现 都是无限不循环小数.
新知讲解
怎样求 的近似值。
新知讲解
算术平方根小数点移动法则
规律:被开方数的小数点每向右(或向左)移动两位,它的算术平方根的小数点就向右(或向左)移动一位.
新知讲解
典型例题
例1:求下列各数的算术平方根.
(1)
(2)
0.0001
(1)因为( )2= ,
所以 的算术平方根为 .
(2)因为(0.01)2=0.0001,
所以0.0001的算术平方根是0.01.
例2:估算 在哪两个整数之间?
解:
∵被求式是在两个整数之间,
典型例题
例3:已知 ≈2.284, ≈7.232,则
(1) ≈ 。
(2)若 ≈0.02284,则x= 。
分析:(1) 向左移动四位就是 ,所以7.232应向左移动两位为0.07232。
(2)2.284向左移动两位为0.02284,所以 需要向左移动四位为 。
0.07232
典型例题
随堂练习
1 .用计算器求下列各式的值。
(1) (精确到0.001)
解:(1)1.732 (2)56.000
(2)
2 .算术平方根等于它本身的数是______;______的算术平方根等于它的相反数。
0和1
0
3 .已知9的算术平方根为a,b的绝对值为4,则a-b的值为________.
-1或7
随堂练习
4 .求下列各数的算术平方根。
(1)(-3)2
(2)
(3)0
(4)
3
0
3
随堂练习
课堂小结
如果一个正数的平方等于a,那么这个正数叫做a的算术平方根.
把a的算术平方根记作 .
a叫做被开方数, 表示a的算术平方根.
注:正数的算术平方根是正数,
0的算术平方根是0,
负数没有算术平方根.
再见
