人教版高中数学选择性必修第三册8.1成对数据的相关关系 同步精练(含解析)
文档属性
| 名称 | 人教版高中数学选择性必修第三册8.1成对数据的相关关系 同步精练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 461.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-14 15:48:16 | ||
图片预览




文档简介
人教版高中数学选择性必修第三册8.1成对数据的相关关系同步精练(原卷版)
【题组一 相关关系】
1.(2021·贵州贵阳市)如下四个散点图中,正相关的是( )
A. B.
C. D.
2.(2021·秦安县第一中学高二期末)根据下面给出的2009年至2018年我国二氧化硫年排放量(单位:万吨)柱形图,以下结论中不正确的是( )
A.逐年比较,2018年减少二氧化硫排放量的效果最显著
B.2012年我国治理二氧化硫排放显现成效
C.2011年以来我国二氧化硫年排放量呈减少趋势
D.2011年以来我国二氧化硫年排放量与年份正相关
3.(2020·全国高三专题练习)某商家今年上半年各月的人均销售额(单位:千元)与利润率统计表如下:
月份 1 2 3 4 5 6
人均销售额 6 5 8 3 4 7
利润率(%) 12.6 10.4 18.5 3.0 8.1 16.3
根据表中数据,下列说法正确的是( )
A.利润率与人均销售额成正相关关系
B.利润率与人均销售额成负相关关系
C.利润率与人均销售额成正比例函数关系
D.利润率与人均销售额成反比例函数关系
4.(2020·青海海东市)下列说法正确的是( )
A.圆的面积与半径之间的关系是相关关系
B.粮食产量与施肥量之间的关系是函数关系
C.一定范围内,学生的成绩与学习时间成正相关关系
D.人的体重与视力成负相关关系
5.(2019·广东广州市·执信中学)对于散点图下列说法正确一个是( )
A.一定可以看出变量之间的变化规律 B.一定不可以看出变量之间的变化规律
C.可以看出正相关与负相关有明显区别 D.看不出正相关与负相关有什么区别
6.(2021·江门市)下列语句表示的事件中的因素不具有相关关系的是( )
A.瑞雪兆丰年 B.名师出高徒 C.不积跬步,无以至千里 D.喜鹊叫喜,乌鸦叫丧
7.(2020·吉林长白山保护开发区教育局高一月考)下列两个变量之间的关系哪个不是函数关系( )
A.角度和它的正切值 B.人的右手一柞长和身高
C.正方体的棱长和表面积 D.真空中自由落体运动物体的下落距离和下落时间
8.(2020·江西赣州市·南康中学高二期中(文))观察下列各图形,
其中两个变量具有相关关系的图是( )
A.①② B.①④ C.③④ D.③
【题组二 样本的相关系数】
1.(2020·广东广州市)在建立两个变量y与x的回归模型,模型的的值依次是0.35,0.67,0.84,0.92,则其中拟合效果最好的模型是( )
A.模型1 B.模型2 C.模型3 D.模型4
2.(2020·河南)有一散点图如图所示,现拟合模型为直线l1,在5个(x,y)数据中去掉D(3,10)后,重新拟合模型为直线l2给出下列说法:①相关系数r变大;②相关指数R2变大;③残差平方和变小;④解释变量x与预报变量y的相关性变强.其中正确说法的个数为( )
A.1个 B.2个 C.3个 D.4个
3.(2020·全国高三专题练习)对于相关系数,下列说法中正确的是( )
A.越大,线性相关程度越强
B.越小,线性相关程度越强
C.越大,线性相关程度越弱,越小,线性相关程度越强
D.,且越接近,线性相关程度越强,越接近,线性相关程度越弱
4.(2020·甘肃省会宁县第一中学)下列结论:①函数关系是一种确定性关系;②相关关系是一种非确定性关系;③回归分析是对具有函数关系的两个变量进行统计分析的一种方法;④回归分析是对具有相关关系的两个变量进行统计分析的一种常用方法.其中正确的是______.(将所有正确的序号填上)
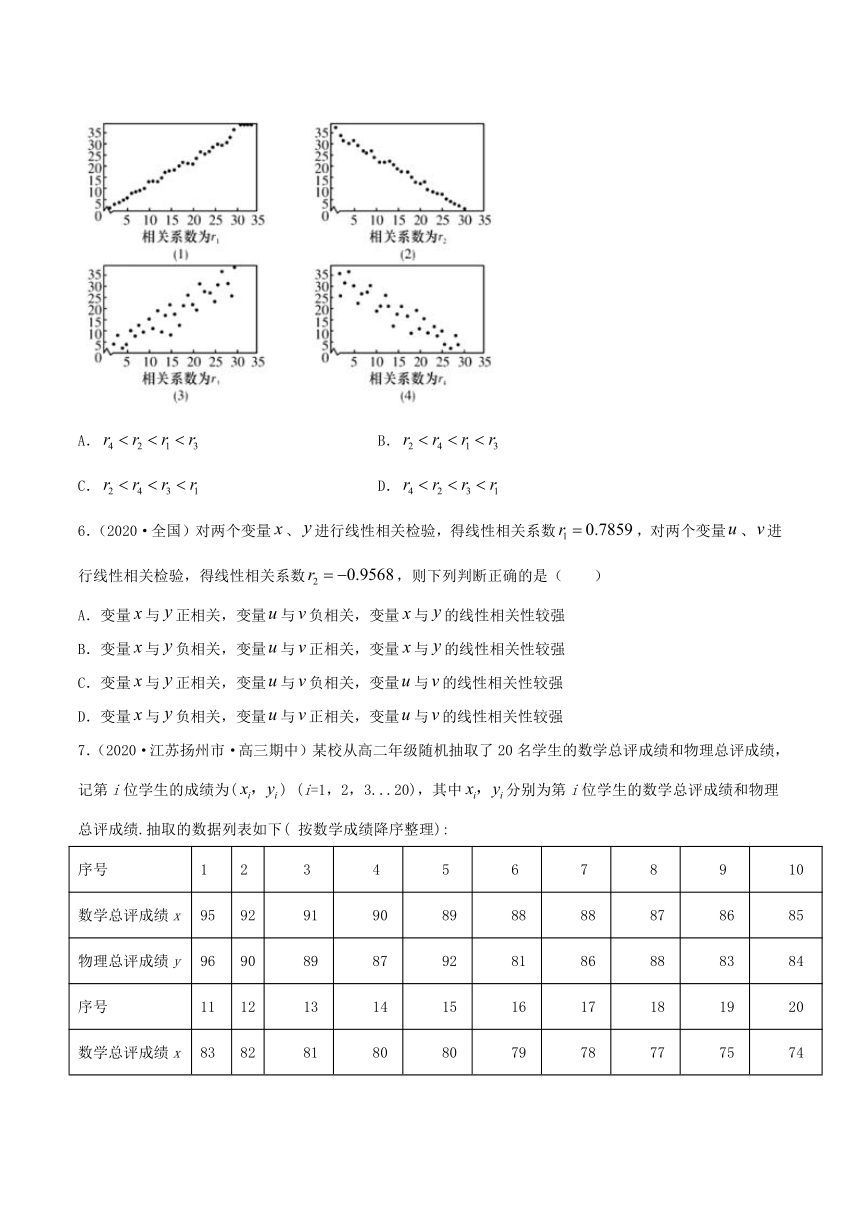
5.(2020·合肥市第六中学高一期末)某统计部门对四组数据进行统计分析后,获得如图所示的散点图,关于相关系数的比较,其中正确的是( )
A. B.
C. D.
6.(2020·全国)对两个变量、进行线性相关检验,得线性相关系数,对两个变量、进行线性相关检验,得线性相关系数,则下列判断正确的是( )
A.变量与正相关,变量与负相关,变量与的线性相关性较强
B.变量与负相关,变量与正相关,变量与的线性相关性较强
C.变量与正相关,变量与负相关,变量与的线性相关性较强
D.变量与负相关,变量与正相关,变量与的线性相关性较强
7.(2020·江苏扬州市·高三期中)某校从高二年级随机抽取了20名学生的数学总评成绩和物理总评成绩,记第i位学生的成绩为() (i=1,2,3...20),其中分别为第i位学生的数学总评成绩和物理总评成绩.抽取的数据列表如下( 按数学成绩降序整理):
序号 1 2 3 4 5 6 7 8 9 10
数学总评成绩x 95 92 91 90 89 88 88 87 86 85
物理总评成绩y 96 90 89 87 92 81 86 88 83 84
序号 11 12 13 14 15 16 17 18 19 20
数学总评成绩x 83 82 81 80 80 79 78 77 75 74
物理总评成绩 81 80 82 85 80 78 79 81 80 78
(1)根据统计学知识,当相关系数|r|≥0.8时,可视为两个变量之间高度相关.根据抽取的数据,能否说明数学总评成绩与物理总评成绩高度相关 请通过计算加以说明.
参考数据:
参考公式:相关系数
(2)规定:总评成绩大于等于85分者为优秀,小于85分者为不优秀,对优秀赋分1,对不优秀赋分0,从这20名学生中随机抽取2名学生,若用X表示这2名学生两科赋分的和,求X的分布列和数学期望.
8.(2020·安徽省太和第一中学)某湿地公园经过近十年的规划和治理,生态系统得到很大改善,野生动物数量有所增加.为调查该地区某种野生动物的数量,将其分成面积相近的300个地块,并设计两种抽样方案,方案一:在该地区应用简单随机抽样的方法抽取30个作为样本区;依据抽样数据计算得到相应的相关系数;方案二:在该地区应用分层抽样的方法抽取30个作为样本区,调查得到样本数据(,2,…,30),其中和分别表示第i个样区的植物覆盖面积(单位:公顷)和这种野生动物的数量,并计算得,,,,.
(1)求该地区这种野生动物数量的估计值(这种野生动物数量的估计值等于样区这种野生动物数量的平均数乘以地块数);
(2)求方案二抽取的样本(,2,…,30)的相关系数(精确到0.01);并判定哪种抽样方法更能准确的估计.
附:相关系数,;相关系数,则相关性很强,的值越大,相关性越强.
9.(2020·湖北荆州市·荆州中学)在我国,大学生就业压力日益严峻,伴随着政府政策引导与社会观念的转变,大学生创业意识,就业方向也悄然发生转变.某大学生在国家提供的税收,担保贷款等很多方面的政策扶持下选择加盟某专营店自主创业,该专营店统计了近五年来创收利润数(单位:万元)与时间(单位:年)的数据,列表如下:
1 2 3 4 5
2.4 2.7 4.1 6.4 7.9
(1)依据表中给出的数据,是否可用线性回归模型拟合与的关系,请计算相关系数并加以说明(计算结果精确到0.01).(若,则线性相关程度很高,可用线性回归模型拟合)
附:相关系数公式:
参考数据:,
(2)谈专营店为吸引顾客,特推出两种促销方案.
方案一:每满500元可减50元;
方案二:每满500元可抽奖一次,每次中奖的概率都为,中奖就可以获得100元现金奖励,假设顾客每次抽奖的结果相互独立.
①某位顾客购买了1050元的产品、该顾客选择参加两次抽奖,求该顾客换得100元现金奖励的概率.
②某位顾客购买了2000元的产品,作为专营店老板,是希望该顾客直接选择返回200元现金,还是选择参加四次抽奖?说明理由.
10.(2020·福建省仙游县枫亭中学)互联网使我们的生活日益便捷,网络外卖也开始成为不少人日常生活中不可或缺的一部分,某市一调查机构针对该市市场占有率较高的甲、乙两家网络外卖企业(以下外卖甲、外卖乙)的经营情况进行了调查,调查结果如下表:
1日 2日 3日 4日 5日
外卖甲日接单x(百单) 5 2 9 8 11
外卖乙日接单y(百单) 2 3 10 5 15
(1)试根据表格中这五天的日接单量情况,从统计的角度说明这两家外卖企业的经营状况;
(2)据统计表明,y与x之间具有线性关系.
①请用相关系数r对y与x之间的相关性强弱进行判断;(若,则可认为y与x有较强的线性相关关系(r值精确到0.001))
②经计算求得y与x之间的回归方程为,假定每单外卖业务企业平均能获纯利润3元,试预测当外卖乙日接单量不低于25百单时,外卖甲所获取的日纯利润的大致范围.(x值精确到0.01)
相关公式:,
参考数据:
人教版高中数学选择性必修第三册8.1成对数据的相关关系同步精练(解析版)
【题组一 相关关系】
1.(2021·贵州贵阳市)如下四个散点图中,正相关的是( )
A. B.
C. D.
【答案】A
【解析】对于A,散点图中的点从左向右是上升的,且在一条直线附近,是正相关;
对于B,散点图中的点从左向右是下降的,且在一条直线附近,是负相关;
对于C、D,散点图中的点不成带状分布,没有明显的相关关系;
故选:A.
2.(2021·秦安县第一中学高二期末)根据下面给出的2009年至2018年我国二氧化硫年排放量(单位:万吨)柱形图,以下结论中不正确的是( )
A.逐年比较,2018年减少二氧化硫排放量的效果最显著
B.2012年我国治理二氧化硫排放显现成效
C.2011年以来我国二氧化硫年排放量呈减少趋势
D.2011年以来我国二氧化硫年排放量与年份正相关
【答案】D
【解析】A. 逐年比较,2018年年排放量最少,故减少二氧化硫排放量的效果最显著;
B. 2012年比2011年二氧化硫年排放量明显减少,故2012年我国治理二氧化硫排放显现成效;
C. 2011年以来每年我国二氧化硫年排放量除2016年外几乎都在减少,故总体呈减少趋势.
D. 2011年以来我国二氧化硫年排放量随年份逐渐减少,与年份负相关,故D错.
故选:D
3.(2020·全国高三专题练习)某商家今年上半年各月的人均销售额(单位:千元)与利润率统计表如下:
月份 1 2 3 4 5 6
人均销售额 6 5 8 3 4 7
利润率(%) 12.6 10.4 18.5 3.0 8.1 16.3
根据表中数据,下列说法正确的是( )
A.利润率与人均销售额成正相关关系
B.利润率与人均销售额成负相关关系
C.利润率与人均销售额成正比例函数关系
D.利润率与人均销售额成反比例函数关系
【答案】A
【解析】画出利润率与人均销售额的散点图,如图.
由图可知利润率与人均销售额成正相关关系.
故选:A.
4.(2020·青海海东市)下列说法正确的是( )
A.圆的面积与半径之间的关系是相关关系
B.粮食产量与施肥量之间的关系是函数关系
C.一定范围内,学生的成绩与学习时间成正相关关系
D.人的体重与视力成负相关关系
【答案】C
【解析】对于A,圆的面积与半径之间的关系是确定的关系,是函数关系,所以A错误;
对于B,粮食产量与施肥量之间的关系是不是函数关系,是相关关系,所以B错误;
对于C,一定范围内,学生的成绩与学习时间是成正相关关系的,所以C正确;
对于D,人的体重与视力是没有相关关系的,所以D错误.
故选:C.
5.(2019·广东广州市·执信中学)对于散点图下列说法正确一个是( )
A.一定可以看出变量之间的变化规律 B.一定不可以看出变量之间的变化规律
C.可以看出正相关与负相关有明显区别 D.看不出正相关与负相关有什么区别
【答案】C
【解析】给出一组样本数据,总可以作出相应的散点图,
但不一定能分析出两个变量的关系,不一定存在回归直线来模拟数据,
但是通过散点图可以看出正相关与负相关有明显区别.
故选:C
6.(2021·江门市)下列语句表示的事件中的因素不具有相关关系的是( )
A.瑞雪兆丰年 B.名师出高徒 C.不积跬步,无以至千里 D.喜鹊叫喜,乌鸦叫丧
【答案】D
【解析】A. 瑞雪对小麦有好处,可能使得小麦丰收,所以瑞雪兆丰年具有相关关系;
B. 名师水平高,可能使得学生学习好,所以名师出高徒具有相关关系;
C. 不积跬步,就不会有千里,所以不积跬步,无以至千里具有相关关系;
D. 喜鹊叫喜,乌鸦叫丧,两者没有必然的关系.
故选:D
7.(2020·吉林长白山保护开发区教育局高一月考)下列两个变量之间的关系哪个不是函数关系( )
A.角度和它的正切值 B.人的右手一柞长和身高
C.正方体的棱长和表面积 D.真空中自由落体运动物体的下落距离和下落时间
【答案】B
【解析】选项,由于角度和正切值有确定的关系;选项,人的右手一柞长和身高不具有统一的关系;选项,正方体的棱长和表面积有关系;选项,真空中自由落体运动物体的下落距离和下落时间有确定的关系.故选:
8.(2020·江西赣州市·南康中学高二期中(文))观察下列各图形,
其中两个变量具有相关关系的图是( )
A.①② B.①④ C.③④ D.③
【答案】C
【解析】由图可知,图③中这些点大致分布在一条直线附近,具有线性相关关系;图④中这些点大致分布在一条类似二次曲线附近,具有相关关系;而图①②中这些点分布不均匀,比较分散,不具有相关关系.
故选:C.
【题组二 样本的相关系数】
1.(2020·广东广州市)在建立两个变量y与x的回归模型,模型的的值依次是0.35,0.67,0.84,0.92,则其中拟合效果最好的模型是( )
A.模型1 B.模型2 C.模型3 D.模型4
【答案】D
【解析】根据相关指数的作用,可知相关指数越大,模型拟合效果越好,
因为,所以模型4的拟合效果最好.故选:D.
2.(2020·河南)有一散点图如图所示,现拟合模型为直线l1,在5个(x,y)数据中去掉D(3,10)后,重新拟合模型为直线l2给出下列说法:①相关系数r变大;②相关指数R2变大;③残差平方和变小;④解释变量x与预报变量y的相关性变强.其中正确说法的个数为( )
A.1个 B.2个 C.3个 D.4个
【答案】D
【解析】由题意,散点图有5个的数据,去掉后,
可得与的相关性越强,并且是正相关,
所以相关系数变大,相关指数变大,残差的平方和变小,
所以四个命题都正确.
故选:D.
3.(2020·全国高三专题练习)对于相关系数,下列说法中正确的是( )
A.越大,线性相关程度越强
B.越小,线性相关程度越强
C.越大,线性相关程度越弱,越小,线性相关程度越强
D.,且越接近,线性相关程度越强,越接近,线性相关程度越弱
【答案】D
【解析】对于选项A,越大,线性相关程度越强,即A错误;
对于选项B,越小,线性相关程度越弱,即B错误;
对于选项C,越大,线性相关程度越强,越小,线性相关程度越弱, 即C错误;
对于选项D,,且越接近,线性相关程度越强,越接近,线性相关程度越弱,即D正确,
故选:D.
4.(2020·甘肃省会宁县第一中学)下列结论:①函数关系是一种确定性关系;②相关关系是一种非确定性关系;③回归分析是对具有函数关系的两个变量进行统计分析的一种方法;④回归分析是对具有相关关系的两个变量进行统计分析的一种常用方法.其中正确的是______.(将所有正确的序号填上)
【答案】①②④
【解析】根据函数关系及相关关系的定义,①函数关系是一种确定性关系.②相关关系是一种非确定性关系.是正确的;由回归分析的定义及应用可知,④回归分析是对具有相关关系的两个变量进行统计分析的一种常用方法.
故答案为:①②④.
5.(2020·合肥市第六中学高一期末)某统计部门对四组数据进行统计分析后,获得如图所示的散点图,关于相关系数的比较,其中正确的是( )
A. B.
C. D.
【答案】C
【解析】根据散点图的特征,数据大致呈增长趋势的是正相关,数据呈递减趋势的是负相关;数据越集中在一条线附近,说明相关性越强,
由题中数据可知:(1)(3)为正相关,(2)(4)为负相关;
故,;,;
又(1)与(2)中散点图更接近于一条直线,故,,
因此,.
故选C.
6.(2020·全国)对两个变量、进行线性相关检验,得线性相关系数,对两个变量、进行线性相关检验,得线性相关系数,则下列判断正确的是( )
A.变量与正相关,变量与负相关,变量与的线性相关性较强
B.变量与负相关,变量与正相关,变量与的线性相关性较强
C.变量与正相关,变量与负相关,变量与的线性相关性较强
D.变量与负相关,变量与正相关,变量与的线性相关性较强
【答案】C
【解析】由线性相关系数知与正相关,
由线性相关系数知与负相关,
又,所以,变量与的线性相关性比与的线性相关性强,
故选:C.
7.(2020·江苏扬州市·高三期中)某校从高二年级随机抽取了20名学生的数学总评成绩和物理总评成绩,记第i位学生的成绩为() (i=1,2,3...20),其中分别为第i位学生的数学总评成绩和物理总评成绩.抽取的数据列表如下( 按数学成绩降序整理):
序号 1 2 3 4 5 6 7 8 9 10
数学总评成绩x 95 92 91 90 89 88 88 87 86 85
物理总评成绩y 96 90 89 87 92 81 86 88 83 84
序号 11 12 13 14 15 16 17 18 19 20
数学总评成绩x 83 82 81 80 80 79 78 77 75 74
物理总评成绩 81 80 82 85 80 78 79 81 80 78
(1)根据统计学知识,当相关系数|r|≥0.8时,可视为两个变量之间高度相关.根据抽取的数据,能否说明数学总评成绩与物理总评成绩高度相关 请通过计算加以说明.
参考数据:
参考公式:相关系数
(2)规定:总评成绩大于等于85分者为优秀,小于85分者为不优秀,对优秀赋分1,对不优秀赋分0,从这20名学生中随机抽取2名学生,若用X表示这2名学生两科赋分的和,求X的分布列和数学期望.
【答案】(1)“数学学期综合成绩”与“物理学期综合成绩”高度相关;答案见解析;(2)分布列见解析,.
【解析】(1)由题意,
,
所以“数学学期综合成绩”与“物理学期综合成绩”高度相关;
(2) 由题意得:的可能取值为0,1,2,3,4.,
根据赋分规则可知,7人赋分为2,4人赋分为1,9个人赋分为0,
所以,,,,,
所以的分布列为:
0 1 2 3 4
所以.
8.(2020·安徽省太和第一中学)某湿地公园经过近十年的规划和治理,生态系统得到很大改善,野生动物数量有所增加.为调查该地区某种野生动物的数量,将其分成面积相近的300个地块,并设计两种抽样方案,方案一:在该地区应用简单随机抽样的方法抽取30个作为样本区;依据抽样数据计算得到相应的相关系数;方案二:在该地区应用分层抽样的方法抽取30个作为样本区,调查得到样本数据(,2,…,30),其中和分别表示第i个样区的植物覆盖面积(单位:公顷)和这种野生动物的数量,并计算得,,,,.
(1)求该地区这种野生动物数量的估计值(这种野生动物数量的估计值等于样区这种野生动物数量的平均数乘以地块数);
(2)求方案二抽取的样本(,2,…,30)的相关系数(精确到0.01);并判定哪种抽样方法更能准确的估计.
附:相关系数,;相关系数,则相关性很强,的值越大,相关性越强.
【答案】(1)12000;(2),方案二的分层抽样方法更能准确的估计.
【解析】(1)由题意可得,样区野生动物平均数为,
又地块数为300,所以该地区这种野生动物的估计值为;
(2)由题中数据可得,
样本(,2,…,30)的相关系数为
.
因为方案一的相关系数为明显小于方案二的相关系数为,
所以方案二的分层抽样方法更能准确的估计.
9.(2020·湖北荆州市·荆州中学)在我国,大学生就业压力日益严峻,伴随着政府政策引导与社会观念的转变,大学生创业意识,就业方向也悄然发生转变.某大学生在国家提供的税收,担保贷款等很多方面的政策扶持下选择加盟某专营店自主创业,该专营店统计了近五年来创收利润数(单位:万元)与时间(单位:年)的数据,列表如下:
1 2 3 4 5
2.4 2.7 4.1 6.4 7.9
(1)依据表中给出的数据,是否可用线性回归模型拟合与的关系,请计算相关系数并加以说明(计算结果精确到0.01).(若,则线性相关程度很高,可用线性回归模型拟合)
附:相关系数公式:
参考数据:,
(2)谈专营店为吸引顾客,特推出两种促销方案.
方案一:每满500元可减50元;
方案二:每满500元可抽奖一次,每次中奖的概率都为,中奖就可以获得100元现金奖励,假设顾客每次抽奖的结果相互独立.
①某位顾客购买了1050元的产品、该顾客选择参加两次抽奖,求该顾客换得100元现金奖励的概率.
②某位顾客购买了2000元的产品,作为专营店老板,是希望该顾客直接选择返回200元现金,还是选择参加四次抽奖?说明理由.
【答案】(1)答案见解析;(2)①;②专营店老板希望该顾客选择参加四次抽奖,理由见解析.
【解析】(1)由题知,,,
.
则
.
故与的线性相关程度很高,可以用线性回归方程拟合;
(2)①顾客选择参加两次抽奖,设他获得100元现金奖励为事件A,
;
②设表示顾客在四次抽奖中中奖的次数,
由于顾客每次抽奖的结果相互独立,则,
∴.
由于顾客每中一次可获得100元现金奖励,
因此顾客在四次抽奖中可获得的奖励金额的均值为.
由于顾客参加四次抽奖获得现金奖励的均值160小于直接返现的200元现金,
故专营店老板希望该顾客选择参加四次抽奖.
10.(2020·福建省仙游县枫亭中学)互联网使我们的生活日益便捷,网络外卖也开始成为不少人日常生活中不可或缺的一部分,某市一调查机构针对该市市场占有率较高的甲、乙两家网络外卖企业(以下外卖甲、外卖乙)的经营情况进行了调查,调查结果如下表:
1日 2日 3日 4日 5日
外卖甲日接单x(百单) 5 2 9 8 11
外卖乙日接单y(百单) 2 3 10 5 15
(1)试根据表格中这五天的日接单量情况,从统计的角度说明这两家外卖企业的经营状况;
(2)据统计表明,y与x之间具有线性关系.
①请用相关系数r对y与x之间的相关性强弱进行判断;(若,则可认为y与x有较强的线性相关关系(r值精确到0.001))
②经计算求得y与x之间的回归方程为,假定每单外卖业务企业平均能获纯利润3元,试预测当外卖乙日接单量不低于25百单时,外卖甲所获取的日纯利润的大致范围.(x值精确到0.01)
相关公式:,
参考数据:.
【答案】(1)外卖甲平均日接单与乙相同﹐但外卖甲日接单量更集中一些,所以外卖甲比外卖乙经营状况更好.(2)①可认为y与x之间有较强的线性相关关系;②外卖甲所获取的日纯利润大约不低于6006元.
【解析】(1)由题可知,(百单),
(百单)
外卖甲的日接单量的方差为,
外卖乙的日接单量的方差,
因为,,即外卖甲平均日接单与乙相同,但外卖甲日接单量更集中一些,所以外卖甲比外卖乙经营状况更好.
(2)①因为
由:
代入计算可得,相关系数
所以可认为y与x之间有较强的线性相关关系;
②令,得
解得,
又,
所以当外卖乙日接单量不低于25百单时,外卖甲所获取的日纯利润大约不低于6006元.
联系QQ309000116加入百度网盘群2500G一线老师必备资料一键转存,自动更新,一劳永逸
【题组一 相关关系】
1.(2021·贵州贵阳市)如下四个散点图中,正相关的是( )
A. B.
C. D.
2.(2021·秦安县第一中学高二期末)根据下面给出的2009年至2018年我国二氧化硫年排放量(单位:万吨)柱形图,以下结论中不正确的是( )
A.逐年比较,2018年减少二氧化硫排放量的效果最显著
B.2012年我国治理二氧化硫排放显现成效
C.2011年以来我国二氧化硫年排放量呈减少趋势
D.2011年以来我国二氧化硫年排放量与年份正相关
3.(2020·全国高三专题练习)某商家今年上半年各月的人均销售额(单位:千元)与利润率统计表如下:
月份 1 2 3 4 5 6
人均销售额 6 5 8 3 4 7
利润率(%) 12.6 10.4 18.5 3.0 8.1 16.3
根据表中数据,下列说法正确的是( )
A.利润率与人均销售额成正相关关系
B.利润率与人均销售额成负相关关系
C.利润率与人均销售额成正比例函数关系
D.利润率与人均销售额成反比例函数关系
4.(2020·青海海东市)下列说法正确的是( )
A.圆的面积与半径之间的关系是相关关系
B.粮食产量与施肥量之间的关系是函数关系
C.一定范围内,学生的成绩与学习时间成正相关关系
D.人的体重与视力成负相关关系
5.(2019·广东广州市·执信中学)对于散点图下列说法正确一个是( )
A.一定可以看出变量之间的变化规律 B.一定不可以看出变量之间的变化规律
C.可以看出正相关与负相关有明显区别 D.看不出正相关与负相关有什么区别
6.(2021·江门市)下列语句表示的事件中的因素不具有相关关系的是( )
A.瑞雪兆丰年 B.名师出高徒 C.不积跬步,无以至千里 D.喜鹊叫喜,乌鸦叫丧
7.(2020·吉林长白山保护开发区教育局高一月考)下列两个变量之间的关系哪个不是函数关系( )
A.角度和它的正切值 B.人的右手一柞长和身高
C.正方体的棱长和表面积 D.真空中自由落体运动物体的下落距离和下落时间
8.(2020·江西赣州市·南康中学高二期中(文))观察下列各图形,
其中两个变量具有相关关系的图是( )
A.①② B.①④ C.③④ D.③
【题组二 样本的相关系数】
1.(2020·广东广州市)在建立两个变量y与x的回归模型,模型的的值依次是0.35,0.67,0.84,0.92,则其中拟合效果最好的模型是( )
A.模型1 B.模型2 C.模型3 D.模型4
2.(2020·河南)有一散点图如图所示,现拟合模型为直线l1,在5个(x,y)数据中去掉D(3,10)后,重新拟合模型为直线l2给出下列说法:①相关系数r变大;②相关指数R2变大;③残差平方和变小;④解释变量x与预报变量y的相关性变强.其中正确说法的个数为( )
A.1个 B.2个 C.3个 D.4个
3.(2020·全国高三专题练习)对于相关系数,下列说法中正确的是( )
A.越大,线性相关程度越强
B.越小,线性相关程度越强
C.越大,线性相关程度越弱,越小,线性相关程度越强
D.,且越接近,线性相关程度越强,越接近,线性相关程度越弱
4.(2020·甘肃省会宁县第一中学)下列结论:①函数关系是一种确定性关系;②相关关系是一种非确定性关系;③回归分析是对具有函数关系的两个变量进行统计分析的一种方法;④回归分析是对具有相关关系的两个变量进行统计分析的一种常用方法.其中正确的是______.(将所有正确的序号填上)
5.(2020·合肥市第六中学高一期末)某统计部门对四组数据进行统计分析后,获得如图所示的散点图,关于相关系数的比较,其中正确的是( )
A. B.
C. D.
6.(2020·全国)对两个变量、进行线性相关检验,得线性相关系数,对两个变量、进行线性相关检验,得线性相关系数,则下列判断正确的是( )
A.变量与正相关,变量与负相关,变量与的线性相关性较强
B.变量与负相关,变量与正相关,变量与的线性相关性较强
C.变量与正相关,变量与负相关,变量与的线性相关性较强
D.变量与负相关,变量与正相关,变量与的线性相关性较强
7.(2020·江苏扬州市·高三期中)某校从高二年级随机抽取了20名学生的数学总评成绩和物理总评成绩,记第i位学生的成绩为() (i=1,2,3...20),其中分别为第i位学生的数学总评成绩和物理总评成绩.抽取的数据列表如下( 按数学成绩降序整理):
序号 1 2 3 4 5 6 7 8 9 10
数学总评成绩x 95 92 91 90 89 88 88 87 86 85
物理总评成绩y 96 90 89 87 92 81 86 88 83 84
序号 11 12 13 14 15 16 17 18 19 20
数学总评成绩x 83 82 81 80 80 79 78 77 75 74
物理总评成绩 81 80 82 85 80 78 79 81 80 78
(1)根据统计学知识,当相关系数|r|≥0.8时,可视为两个变量之间高度相关.根据抽取的数据,能否说明数学总评成绩与物理总评成绩高度相关 请通过计算加以说明.
参考数据:
参考公式:相关系数
(2)规定:总评成绩大于等于85分者为优秀,小于85分者为不优秀,对优秀赋分1,对不优秀赋分0,从这20名学生中随机抽取2名学生,若用X表示这2名学生两科赋分的和,求X的分布列和数学期望.
8.(2020·安徽省太和第一中学)某湿地公园经过近十年的规划和治理,生态系统得到很大改善,野生动物数量有所增加.为调查该地区某种野生动物的数量,将其分成面积相近的300个地块,并设计两种抽样方案,方案一:在该地区应用简单随机抽样的方法抽取30个作为样本区;依据抽样数据计算得到相应的相关系数;方案二:在该地区应用分层抽样的方法抽取30个作为样本区,调查得到样本数据(,2,…,30),其中和分别表示第i个样区的植物覆盖面积(单位:公顷)和这种野生动物的数量,并计算得,,,,.
(1)求该地区这种野生动物数量的估计值(这种野生动物数量的估计值等于样区这种野生动物数量的平均数乘以地块数);
(2)求方案二抽取的样本(,2,…,30)的相关系数(精确到0.01);并判定哪种抽样方法更能准确的估计.
附:相关系数,;相关系数,则相关性很强,的值越大,相关性越强.
9.(2020·湖北荆州市·荆州中学)在我国,大学生就业压力日益严峻,伴随着政府政策引导与社会观念的转变,大学生创业意识,就业方向也悄然发生转变.某大学生在国家提供的税收,担保贷款等很多方面的政策扶持下选择加盟某专营店自主创业,该专营店统计了近五年来创收利润数(单位:万元)与时间(单位:年)的数据,列表如下:
1 2 3 4 5
2.4 2.7 4.1 6.4 7.9
(1)依据表中给出的数据,是否可用线性回归模型拟合与的关系,请计算相关系数并加以说明(计算结果精确到0.01).(若,则线性相关程度很高,可用线性回归模型拟合)
附:相关系数公式:
参考数据:,
(2)谈专营店为吸引顾客,特推出两种促销方案.
方案一:每满500元可减50元;
方案二:每满500元可抽奖一次,每次中奖的概率都为,中奖就可以获得100元现金奖励,假设顾客每次抽奖的结果相互独立.
①某位顾客购买了1050元的产品、该顾客选择参加两次抽奖,求该顾客换得100元现金奖励的概率.
②某位顾客购买了2000元的产品,作为专营店老板,是希望该顾客直接选择返回200元现金,还是选择参加四次抽奖?说明理由.
10.(2020·福建省仙游县枫亭中学)互联网使我们的生活日益便捷,网络外卖也开始成为不少人日常生活中不可或缺的一部分,某市一调查机构针对该市市场占有率较高的甲、乙两家网络外卖企业(以下外卖甲、外卖乙)的经营情况进行了调查,调查结果如下表:
1日 2日 3日 4日 5日
外卖甲日接单x(百单) 5 2 9 8 11
外卖乙日接单y(百单) 2 3 10 5 15
(1)试根据表格中这五天的日接单量情况,从统计的角度说明这两家外卖企业的经营状况;
(2)据统计表明,y与x之间具有线性关系.
①请用相关系数r对y与x之间的相关性强弱进行判断;(若,则可认为y与x有较强的线性相关关系(r值精确到0.001))
②经计算求得y与x之间的回归方程为,假定每单外卖业务企业平均能获纯利润3元,试预测当外卖乙日接单量不低于25百单时,外卖甲所获取的日纯利润的大致范围.(x值精确到0.01)
相关公式:,
参考数据:
人教版高中数学选择性必修第三册8.1成对数据的相关关系同步精练(解析版)
【题组一 相关关系】
1.(2021·贵州贵阳市)如下四个散点图中,正相关的是( )
A. B.
C. D.
【答案】A
【解析】对于A,散点图中的点从左向右是上升的,且在一条直线附近,是正相关;
对于B,散点图中的点从左向右是下降的,且在一条直线附近,是负相关;
对于C、D,散点图中的点不成带状分布,没有明显的相关关系;
故选:A.
2.(2021·秦安县第一中学高二期末)根据下面给出的2009年至2018年我国二氧化硫年排放量(单位:万吨)柱形图,以下结论中不正确的是( )
A.逐年比较,2018年减少二氧化硫排放量的效果最显著
B.2012年我国治理二氧化硫排放显现成效
C.2011年以来我国二氧化硫年排放量呈减少趋势
D.2011年以来我国二氧化硫年排放量与年份正相关
【答案】D
【解析】A. 逐年比较,2018年年排放量最少,故减少二氧化硫排放量的效果最显著;
B. 2012年比2011年二氧化硫年排放量明显减少,故2012年我国治理二氧化硫排放显现成效;
C. 2011年以来每年我国二氧化硫年排放量除2016年外几乎都在减少,故总体呈减少趋势.
D. 2011年以来我国二氧化硫年排放量随年份逐渐减少,与年份负相关,故D错.
故选:D
3.(2020·全国高三专题练习)某商家今年上半年各月的人均销售额(单位:千元)与利润率统计表如下:
月份 1 2 3 4 5 6
人均销售额 6 5 8 3 4 7
利润率(%) 12.6 10.4 18.5 3.0 8.1 16.3
根据表中数据,下列说法正确的是( )
A.利润率与人均销售额成正相关关系
B.利润率与人均销售额成负相关关系
C.利润率与人均销售额成正比例函数关系
D.利润率与人均销售额成反比例函数关系
【答案】A
【解析】画出利润率与人均销售额的散点图,如图.
由图可知利润率与人均销售额成正相关关系.
故选:A.
4.(2020·青海海东市)下列说法正确的是( )
A.圆的面积与半径之间的关系是相关关系
B.粮食产量与施肥量之间的关系是函数关系
C.一定范围内,学生的成绩与学习时间成正相关关系
D.人的体重与视力成负相关关系
【答案】C
【解析】对于A,圆的面积与半径之间的关系是确定的关系,是函数关系,所以A错误;
对于B,粮食产量与施肥量之间的关系是不是函数关系,是相关关系,所以B错误;
对于C,一定范围内,学生的成绩与学习时间是成正相关关系的,所以C正确;
对于D,人的体重与视力是没有相关关系的,所以D错误.
故选:C.
5.(2019·广东广州市·执信中学)对于散点图下列说法正确一个是( )
A.一定可以看出变量之间的变化规律 B.一定不可以看出变量之间的变化规律
C.可以看出正相关与负相关有明显区别 D.看不出正相关与负相关有什么区别
【答案】C
【解析】给出一组样本数据,总可以作出相应的散点图,
但不一定能分析出两个变量的关系,不一定存在回归直线来模拟数据,
但是通过散点图可以看出正相关与负相关有明显区别.
故选:C
6.(2021·江门市)下列语句表示的事件中的因素不具有相关关系的是( )
A.瑞雪兆丰年 B.名师出高徒 C.不积跬步,无以至千里 D.喜鹊叫喜,乌鸦叫丧
【答案】D
【解析】A. 瑞雪对小麦有好处,可能使得小麦丰收,所以瑞雪兆丰年具有相关关系;
B. 名师水平高,可能使得学生学习好,所以名师出高徒具有相关关系;
C. 不积跬步,就不会有千里,所以不积跬步,无以至千里具有相关关系;
D. 喜鹊叫喜,乌鸦叫丧,两者没有必然的关系.
故选:D
7.(2020·吉林长白山保护开发区教育局高一月考)下列两个变量之间的关系哪个不是函数关系( )
A.角度和它的正切值 B.人的右手一柞长和身高
C.正方体的棱长和表面积 D.真空中自由落体运动物体的下落距离和下落时间
【答案】B
【解析】选项,由于角度和正切值有确定的关系;选项,人的右手一柞长和身高不具有统一的关系;选项,正方体的棱长和表面积有关系;选项,真空中自由落体运动物体的下落距离和下落时间有确定的关系.故选:
8.(2020·江西赣州市·南康中学高二期中(文))观察下列各图形,
其中两个变量具有相关关系的图是( )
A.①② B.①④ C.③④ D.③
【答案】C
【解析】由图可知,图③中这些点大致分布在一条直线附近,具有线性相关关系;图④中这些点大致分布在一条类似二次曲线附近,具有相关关系;而图①②中这些点分布不均匀,比较分散,不具有相关关系.
故选:C.
【题组二 样本的相关系数】
1.(2020·广东广州市)在建立两个变量y与x的回归模型,模型的的值依次是0.35,0.67,0.84,0.92,则其中拟合效果最好的模型是( )
A.模型1 B.模型2 C.模型3 D.模型4
【答案】D
【解析】根据相关指数的作用,可知相关指数越大,模型拟合效果越好,
因为,所以模型4的拟合效果最好.故选:D.
2.(2020·河南)有一散点图如图所示,现拟合模型为直线l1,在5个(x,y)数据中去掉D(3,10)后,重新拟合模型为直线l2给出下列说法:①相关系数r变大;②相关指数R2变大;③残差平方和变小;④解释变量x与预报变量y的相关性变强.其中正确说法的个数为( )
A.1个 B.2个 C.3个 D.4个
【答案】D
【解析】由题意,散点图有5个的数据,去掉后,
可得与的相关性越强,并且是正相关,
所以相关系数变大,相关指数变大,残差的平方和变小,
所以四个命题都正确.
故选:D.
3.(2020·全国高三专题练习)对于相关系数,下列说法中正确的是( )
A.越大,线性相关程度越强
B.越小,线性相关程度越强
C.越大,线性相关程度越弱,越小,线性相关程度越强
D.,且越接近,线性相关程度越强,越接近,线性相关程度越弱
【答案】D
【解析】对于选项A,越大,线性相关程度越强,即A错误;
对于选项B,越小,线性相关程度越弱,即B错误;
对于选项C,越大,线性相关程度越强,越小,线性相关程度越弱, 即C错误;
对于选项D,,且越接近,线性相关程度越强,越接近,线性相关程度越弱,即D正确,
故选:D.
4.(2020·甘肃省会宁县第一中学)下列结论:①函数关系是一种确定性关系;②相关关系是一种非确定性关系;③回归分析是对具有函数关系的两个变量进行统计分析的一种方法;④回归分析是对具有相关关系的两个变量进行统计分析的一种常用方法.其中正确的是______.(将所有正确的序号填上)
【答案】①②④
【解析】根据函数关系及相关关系的定义,①函数关系是一种确定性关系.②相关关系是一种非确定性关系.是正确的;由回归分析的定义及应用可知,④回归分析是对具有相关关系的两个变量进行统计分析的一种常用方法.
故答案为:①②④.
5.(2020·合肥市第六中学高一期末)某统计部门对四组数据进行统计分析后,获得如图所示的散点图,关于相关系数的比较,其中正确的是( )
A. B.
C. D.
【答案】C
【解析】根据散点图的特征,数据大致呈增长趋势的是正相关,数据呈递减趋势的是负相关;数据越集中在一条线附近,说明相关性越强,
由题中数据可知:(1)(3)为正相关,(2)(4)为负相关;
故,;,;
又(1)与(2)中散点图更接近于一条直线,故,,
因此,.
故选C.
6.(2020·全国)对两个变量、进行线性相关检验,得线性相关系数,对两个变量、进行线性相关检验,得线性相关系数,则下列判断正确的是( )
A.变量与正相关,变量与负相关,变量与的线性相关性较强
B.变量与负相关,变量与正相关,变量与的线性相关性较强
C.变量与正相关,变量与负相关,变量与的线性相关性较强
D.变量与负相关,变量与正相关,变量与的线性相关性较强
【答案】C
【解析】由线性相关系数知与正相关,
由线性相关系数知与负相关,
又,所以,变量与的线性相关性比与的线性相关性强,
故选:C.
7.(2020·江苏扬州市·高三期中)某校从高二年级随机抽取了20名学生的数学总评成绩和物理总评成绩,记第i位学生的成绩为() (i=1,2,3...20),其中分别为第i位学生的数学总评成绩和物理总评成绩.抽取的数据列表如下( 按数学成绩降序整理):
序号 1 2 3 4 5 6 7 8 9 10
数学总评成绩x 95 92 91 90 89 88 88 87 86 85
物理总评成绩y 96 90 89 87 92 81 86 88 83 84
序号 11 12 13 14 15 16 17 18 19 20
数学总评成绩x 83 82 81 80 80 79 78 77 75 74
物理总评成绩 81 80 82 85 80 78 79 81 80 78
(1)根据统计学知识,当相关系数|r|≥0.8时,可视为两个变量之间高度相关.根据抽取的数据,能否说明数学总评成绩与物理总评成绩高度相关 请通过计算加以说明.
参考数据:
参考公式:相关系数
(2)规定:总评成绩大于等于85分者为优秀,小于85分者为不优秀,对优秀赋分1,对不优秀赋分0,从这20名学生中随机抽取2名学生,若用X表示这2名学生两科赋分的和,求X的分布列和数学期望.
【答案】(1)“数学学期综合成绩”与“物理学期综合成绩”高度相关;答案见解析;(2)分布列见解析,.
【解析】(1)由题意,
,
所以“数学学期综合成绩”与“物理学期综合成绩”高度相关;
(2) 由题意得:的可能取值为0,1,2,3,4.,
根据赋分规则可知,7人赋分为2,4人赋分为1,9个人赋分为0,
所以,,,,,
所以的分布列为:
0 1 2 3 4
所以.
8.(2020·安徽省太和第一中学)某湿地公园经过近十年的规划和治理,生态系统得到很大改善,野生动物数量有所增加.为调查该地区某种野生动物的数量,将其分成面积相近的300个地块,并设计两种抽样方案,方案一:在该地区应用简单随机抽样的方法抽取30个作为样本区;依据抽样数据计算得到相应的相关系数;方案二:在该地区应用分层抽样的方法抽取30个作为样本区,调查得到样本数据(,2,…,30),其中和分别表示第i个样区的植物覆盖面积(单位:公顷)和这种野生动物的数量,并计算得,,,,.
(1)求该地区这种野生动物数量的估计值(这种野生动物数量的估计值等于样区这种野生动物数量的平均数乘以地块数);
(2)求方案二抽取的样本(,2,…,30)的相关系数(精确到0.01);并判定哪种抽样方法更能准确的估计.
附:相关系数,;相关系数,则相关性很强,的值越大,相关性越强.
【答案】(1)12000;(2),方案二的分层抽样方法更能准确的估计.
【解析】(1)由题意可得,样区野生动物平均数为,
又地块数为300,所以该地区这种野生动物的估计值为;
(2)由题中数据可得,
样本(,2,…,30)的相关系数为
.
因为方案一的相关系数为明显小于方案二的相关系数为,
所以方案二的分层抽样方法更能准确的估计.
9.(2020·湖北荆州市·荆州中学)在我国,大学生就业压力日益严峻,伴随着政府政策引导与社会观念的转变,大学生创业意识,就业方向也悄然发生转变.某大学生在国家提供的税收,担保贷款等很多方面的政策扶持下选择加盟某专营店自主创业,该专营店统计了近五年来创收利润数(单位:万元)与时间(单位:年)的数据,列表如下:
1 2 3 4 5
2.4 2.7 4.1 6.4 7.9
(1)依据表中给出的数据,是否可用线性回归模型拟合与的关系,请计算相关系数并加以说明(计算结果精确到0.01).(若,则线性相关程度很高,可用线性回归模型拟合)
附:相关系数公式:
参考数据:,
(2)谈专营店为吸引顾客,特推出两种促销方案.
方案一:每满500元可减50元;
方案二:每满500元可抽奖一次,每次中奖的概率都为,中奖就可以获得100元现金奖励,假设顾客每次抽奖的结果相互独立.
①某位顾客购买了1050元的产品、该顾客选择参加两次抽奖,求该顾客换得100元现金奖励的概率.
②某位顾客购买了2000元的产品,作为专营店老板,是希望该顾客直接选择返回200元现金,还是选择参加四次抽奖?说明理由.
【答案】(1)答案见解析;(2)①;②专营店老板希望该顾客选择参加四次抽奖,理由见解析.
【解析】(1)由题知,,,
.
则
.
故与的线性相关程度很高,可以用线性回归方程拟合;
(2)①顾客选择参加两次抽奖,设他获得100元现金奖励为事件A,
;
②设表示顾客在四次抽奖中中奖的次数,
由于顾客每次抽奖的结果相互独立,则,
∴.
由于顾客每中一次可获得100元现金奖励,
因此顾客在四次抽奖中可获得的奖励金额的均值为.
由于顾客参加四次抽奖获得现金奖励的均值160小于直接返现的200元现金,
故专营店老板希望该顾客选择参加四次抽奖.
10.(2020·福建省仙游县枫亭中学)互联网使我们的生活日益便捷,网络外卖也开始成为不少人日常生活中不可或缺的一部分,某市一调查机构针对该市市场占有率较高的甲、乙两家网络外卖企业(以下外卖甲、外卖乙)的经营情况进行了调查,调查结果如下表:
1日 2日 3日 4日 5日
外卖甲日接单x(百单) 5 2 9 8 11
外卖乙日接单y(百单) 2 3 10 5 15
(1)试根据表格中这五天的日接单量情况,从统计的角度说明这两家外卖企业的经营状况;
(2)据统计表明,y与x之间具有线性关系.
①请用相关系数r对y与x之间的相关性强弱进行判断;(若,则可认为y与x有较强的线性相关关系(r值精确到0.001))
②经计算求得y与x之间的回归方程为,假定每单外卖业务企业平均能获纯利润3元,试预测当外卖乙日接单量不低于25百单时,外卖甲所获取的日纯利润的大致范围.(x值精确到0.01)
相关公式:,
参考数据:.
【答案】(1)外卖甲平均日接单与乙相同﹐但外卖甲日接单量更集中一些,所以外卖甲比外卖乙经营状况更好.(2)①可认为y与x之间有较强的线性相关关系;②外卖甲所获取的日纯利润大约不低于6006元.
【解析】(1)由题可知,(百单),
(百单)
外卖甲的日接单量的方差为,
外卖乙的日接单量的方差,
因为,,即外卖甲平均日接单与乙相同,但外卖甲日接单量更集中一些,所以外卖甲比外卖乙经营状况更好.
(2)①因为
由:
代入计算可得,相关系数
所以可认为y与x之间有较强的线性相关关系;
②令,得
解得,
又,
所以当外卖乙日接单量不低于25百单时,外卖甲所获取的日纯利润大约不低于6006元.
联系QQ309000116加入百度网盘群2500G一线老师必备资料一键转存,自动更新,一劳永逸
