2022-2023学年河北省保定市顺平县七年级(下)期末数学试卷(含解析)
文档属性
| 名称 | 2022-2023学年河北省保定市顺平县七年级(下)期末数学试卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 294.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-14 00:00:00 | ||
图片预览



文档简介
2022-2023学年河北省保定市顺平县七年级(下)期末数学试卷
一、选择题(本大题共16小题,共42.0分。在每小题列出的选项中,选出符合题目的一项)
1. 以下调查中,最适合采用全面调查的是( )
A. 检测神舟飞船零部件质量情况 B. 了解河北中小学生课外阅读情况
C. 调查某批次牛奶的质量 D. 中央电视台开学第一课的收视率
2. 下列各式计算正确的是( )
A. B. C. D.
3. 如图,直线,被直线所截,下列条件不能判定直线的是( )
A.
B.
C.
D.
4. 若,则点在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
5. 如果,那么下列不等式正确的是( )
A. B. C. D.
6. 已知二元一次方程的一个解是,则的值为( )
A. B. C. D.
7. 用加减消元法解二元一次方程组时,下列方法中无法消元的是( )
A. B. C. D.
8. 不等式组的解集,在数轴上表示正确的是( )
A. B.
C. D.
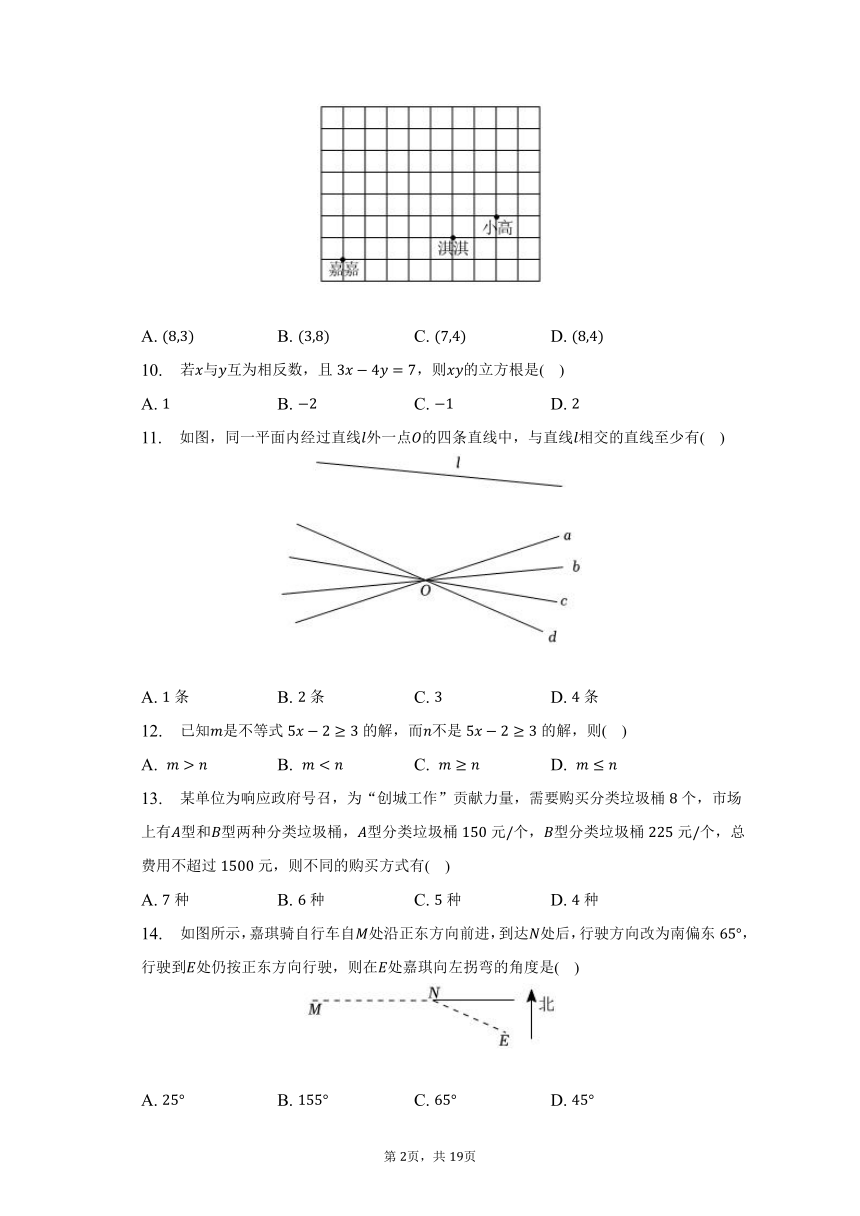
9. 某天课间操时,嘉嘉、淇淇、小高的位置如图所示,嘉嘉对小高说:“如果我的位置用表示,淇淇的位置用表示,那么你的位置可以表示成什么?”( )
A. B. C. D.
10. 若与互为相反数,且,则的立方根是( )
A. B. C. D.
11. 如图,同一平面内经过直线外一点的四条直线中,与直线相交的直线至少有( )
A. 条 B. 条 C. D. 条
12. 已知是不等式的解,而不是的解,则( )
A. B. C. D.
13. 某单位为响应政府号召,为“创城工作”贡献力量,需要购买分类垃圾桶个,市场上有型和型两种分类垃圾桶,型分类垃圾桶元个,型分类垃圾桶元个,总费用不超过元,则不同的购买方式有( )
A. 种 B. 种 C. 种 D. 种
14. 如图所示,嘉琪骑自行车自处沿正东方向前进,到达处后,行驶方向改为南偏东,行驶到处仍按正东方向行驶,则在处嘉琪向左拐弯的角度是( )
A. B. C. D.
15. 为了了解参加某运动会的名运动员的年龄情况,从中抽取了名运动员的年龄,就这个问题来说,下面说法正确的是( )
A. 名运动员是总体 B. 名运动员是所抽取的一个样本
C. 样本容量为名 D. 抽取的名运动员的年龄是样本
16. 我国古代数学名著九章算术中有一道题,原文是:“今有善行者行一百步,不善行者行六十步今不善行者先行一百步,善行者追之,问几何步及之?”意思是:同样时间段内,走路快的人能走步,走路慢的人只能走步走路慢的人先走步,随后走路快的人出发去追他,那么走路快的人走多少步才能追上走路慢的人?设走路快的人走步才能追上走路慢的人,此时走路慢的人走了步,则正确的方程组是( )
A. B. C. D.
二、填空题(本大题共3小题,共9.0分)
17. 在,,,,,,,,中是无理数的个数有______ 个.
18. 某营养快餐的成分为:蛋白质、脂肪、矿物质、碳水化合物其中脂肪所占的百分比为,所含蛋白质质量是矿物质质量的倍,若这种快餐总质量是克,则:
快餐中所含脂肪的质量是______ 克;
若这份快餐中蛋白质和碳水化合物所占百分比的和不高于,则所含碳水化合物最多有______ 克
19. 阅读感悟:有些关于方程组的问题,欲求的结果不是每一个未知数的值,而是关于未知数的式子的值,如以下问题:
已知实数、满足,,求和的值.
本题常规思路是将两式联立组成方程组,解得、的值再代入欲求值的整式得到答案,常规思路运算量比较大其实,仔细观察两个方程未知数的系数之间的关系,本题还可以通过适当变形整体求得整式的值,如由可得,由可得这样的解题思想就是通常所说的“整体思想”利用上面的知识解答下列问题:
已知、满足方程组,则的值为______ ,的值为______ ;
已知方程组的解是,则方程组的解是______ .
三、解答题(本大题共7小题,共69.0分。解答应写出文字说明,证明过程或演算步骤)
20. 本小题分
计算:;
已知的平方根是,的立方根是,求的平方根.
21. 本小题分
已知整式,当时,.
若,求、的值;
在的条件下,若,直接写出的最大整数值.
22. 本小题分
如图,直线与相交于点,直线与直线相交于点,且平分,且,.
求的度数;
若平分,求的度数.
23. 本小题分
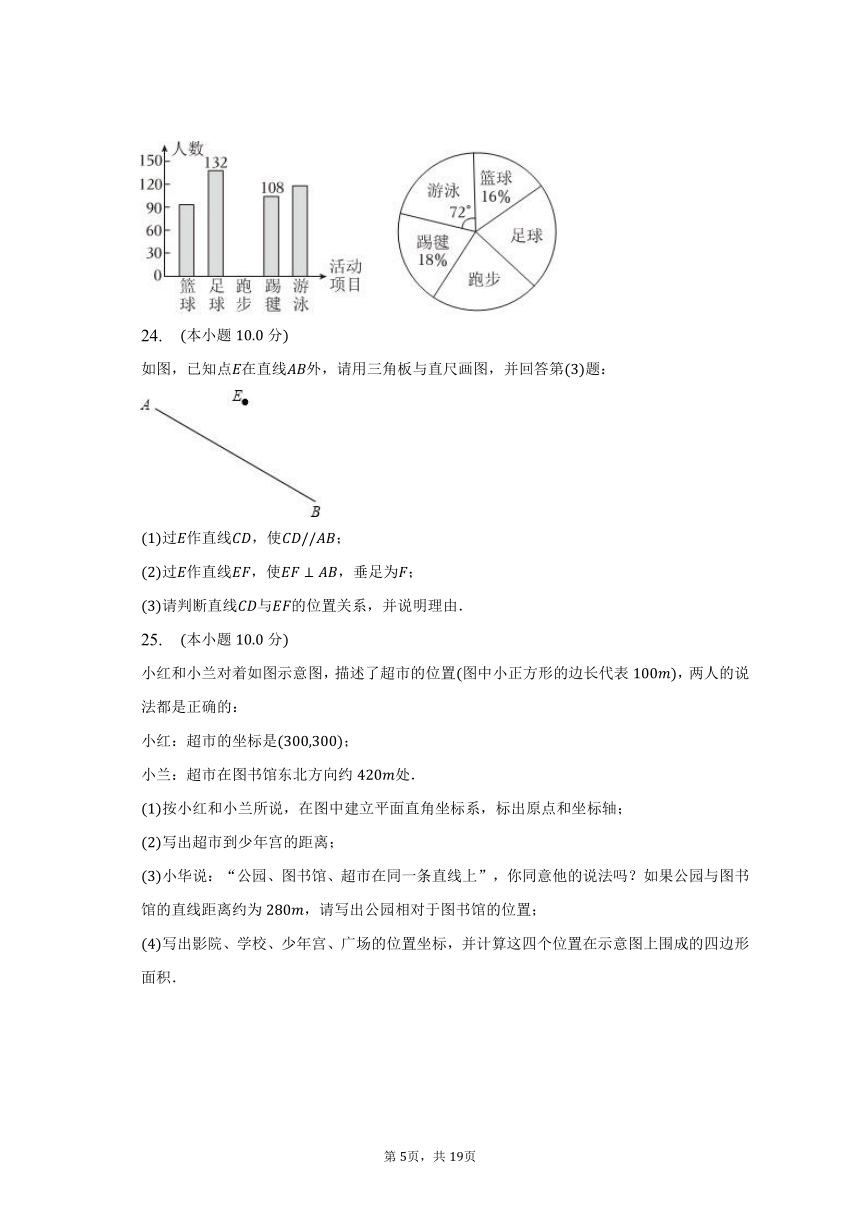
为了丰富校园生活,推进校园服务,某中学在课后延时服务中,开展了一系列体育活动,为了调查哪项活动最受学生欢迎,中学团委对七年级学生进行了问卷调查,针对该项调查结果制作的两个统计图不完整,如图.
本次调查的样本容量是多少?
选择“游泳”活动的人数是多少?
通过计算补全条形统计图;
调查中,哪项活动最受学生欢迎,估计全校名学生中喜欢这项活动的有多少人?
24. 本小题分
如图,已知点在直线外,请用三角板与直尺画图,并回答第题:
过作直线,使;
过作直线,使,垂足为;
请判断直线与的位置关系,并说明理由.
25. 本小题分
小红和小兰对着如图示意图,描述了超市的位置图中小正方形的边长代表,两人的说法都是正确的:
小红:超市的坐标是;
小兰:超市在图书馆东北方向约处.
按小红和小兰所说,在图中建立平面直角坐标系,标出原点和坐标轴;
写出超市到少年宫的距离;
小华说:“公园、图书馆、超市在同一条直线上”,你同意他的说法吗?如果公园与图书馆的直线距离约为,请写出公园相对于图书馆的位置;
写出影院、学校、少年宫、广场的位置坐标,并计算这四个位置在示意图上围成的四边形面积.
26. 本小题分
某服装店欲一次性购进、两种童衣共件进行销售其中种童衣件,种童衣件,进价总额为元;种童衣件,种童衣件,进价总额为元,种童衣每件售价元,种童衣每件售价元.
求两种童衣的每件进价分别是多少元?
若每种童衣各购进件,求销售完这批童衣的销售利润;
由于资金等因素限制,实际购进的种童衣不少于种童衣的倍,那么购进种童衣最多为多少件?并求此时销售完这批童衣的销售利润.
答案和解析
1.【答案】
【解析】解:检测神舟飞船零部件质量情况,适合全面调查,故本选项符合题意;
B.了解河北中小学生课外阅读情况,适合抽样调查,故本选项不符合题意;
C.调查某批次牛奶的质量,适合抽样调查,故本选项不符合题意;
D.中央电视台开学第一课的收视率,适合抽样调查,故本选项不符合题意.
故选:.
根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似解答.
本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
2.【答案】
【解析】解:,因此选项A不符合题意;
B.,因此选项B符合题意;
C.,因此选项C不符合题意;
D.,因此选项D不符合题意;
故选:.
根据立方根,二次根式的性质和化简逐项进行计算即可.
本题考查二次根式的性质,立方根,理解立方根的定义,掌握二次根式的性质是正确解答的前提.
3.【答案】
【解析】解:由,不能判定,
故A符合题意;
,,
,
,
,
,
故B不符合题意;
,,
,
,
故C不符合题意;
,
,
故D不符合题意;
故选:.
根据平行线的判定定理判断求解即可.
此题考查了平行线的判定,熟记平行线的判定定理是解题的关键.
4.【答案】
【解析】解:,,,
,,
即,,
在第四象限,
故选:.
根据绝对值、偶次幂的非负性求出、的值,确定点的坐标,再根据直角坐标系中点的坐标与位置的关系进行解答即可.
本题考查绝对值、偶次方的非负性以及平面直角坐标系,理解绝对值、偶次方的非负性以及点的坐标特征是正确解答的前提.
5.【答案】
【解析】解:,
,
选项A符合题意;
,
,
选项B不符合题意;
,
,
选项C不符合题意;
,
,
选项D不符合题意.
故选:.
根据,应用不等式的性质,逐项判断即可.
此题主要考查了不等式的基本性质:不等式的两边同时加上或减去同一个数或同一个含有字母的式子,不等号的方向不变;不等式的两边同时乘或除以同一个正数,不等号的方向不变;不等式的两边同时乘或除以同一个负数,不等号的方向改变.
6.【答案】
【解析】解:把代入,得
,
,
.
故选:.
把代入,然后解关于的方程即可.
本题考查了求二元一次方程的解,能使二元一次方程左右两边相等的未知数的值叫做二元一次方程的解.
7.【答案】
【解析】解:用加减消元法解二元一次方程组时,
消去;消去;消去;消去,
则无法消元.
故选:.
利用加减消元法判断即可.
此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.
8.【答案】
【解析】解:,
解不等式得:;
解不等式得:;
不等式组的解集为,
数轴上表示为:
故选:.
解出每个不等式的解集,再求公共解集,把解集表示在数轴上即可.
本题考查解一元一次不等式组,解题的关键是掌握求公共解集的方法.
9.【答案】
【解析】解:如图所示:淇淇的位置用表示,
小高的位置为:.
故选:.
根据淇淇的位置用确定平面直角坐标系,然后确定小高的位置坐标.
此题主要考查了坐标确定位置,利用原点的位置得出是解题关键.
10.【答案】
【解析】解:由题意得,
,
,
,
,
,
,
,
的立方根是.
故选:.
由题意得,根据等式的性质,加上再减去,消去,得出的值,再得出的值,进行求解.
此题考查了有理数的相反数和有理数乘法的运用能力,关键是能准确理解并运用以上知识进行正确地计算.
11.【答案】
【解析】解:过直线外一点,有且只有一条直线与已知直线平行,
过直线外一点的四条直线中,最多只有一条直线与平行,
与直线相交的直线至少有条,
故选:.
由平行公理,即可判断.
本题考查平行公理,关键是掌握平行公理.
12.【答案】
【解析】解:是不等式的解,
,
解得,
不是的解,
,
解得,
,
故选:.
求出,,即可得.
本题考查解一元一次不等式,解题的关键是掌握一元一次不等式的解的定义.
13.【答案】
【解析】解:设购买个型分类垃圾桶,则购买个型分类垃圾桶,
根据题意得:,
解得:,
又,均为自然数,
可以为,,,,,
共有种不同的购买方案.
故选:.
设购买个型分类垃圾桶,则购买个型分类垃圾桶,利用总价单价数量,结合总价不超过元,可列出关于的一元一次不等式,解之可得出的取值范围,再结合,均为自然数,即可得出共有种不同的购买方案.
本题考查了一元一次不等式的应用,根据各数量之间的关系,正确列出一元一次不等式是解题的关键.
14.【答案】
【解析】解:如图,嘉琪行驶到处仍按正东方向行驶,即方向行驶,
嘉琪骑自行车自处沿正东方向前进,到达处后,行驶方向改为南偏东,
,
,
,
即在处嘉琪向左拐弯的角度是,
故选:.
根据“两直线平行,同位角相等”求解即可.
此题考查了平行线的性质,熟记平行线的性质定理是解题的关键.
15.【答案】
【解析】解:、名运动员的年龄是总体,原说法错误,故本选项错误;
B、名运动员的年龄是所抽取的一个样本,原说法错误,故本选项错误;
C、样本容量为,原说法错误,故本选项错误;
D、抽取的名运动员的年龄是样本,说法正确,故本选项正确;
故选D.
总体:我们把所要考察的对象的全体叫做总体;
个体:把组成总体的每一个考察对象叫做个体;
样本:从总体中取出的一部分个体叫做这个总体的一个样本;
样本容量:一个样本包括的个体数量叫做样本容量.
结合选项进行判断即可.
本题考查了总体、样本及样本容量的知识,属于基础题,掌握基本定义是关键.
16.【答案】
【解析】解:由题意得:
,
故选:.
根据“同样时间段内,走路快的人能走步,走路慢的人只能走步”和“走路慢的人先走步,”列方程组求解.
本题考查了二元一次方程组的应用,找到线相等关系是解题的关键.
17.【答案】
【解析】
【分析】
本题主要考查的是无理数的认识,掌握无理数常见类型是解题的关键.无理数常见的三种类型开不尽的方根,;特定结构的无限不循环小数,如两个之间依次多一个;含有的绝大部分数,如.
【解答】
解:是有理数,是一个有限小数,是有理数,是无理数,是有理数,是无理数,是有理数,是有理数,是有理数,是无理数.
故答案为.
18.【答案】
【解析】解:由题意可得,
快餐中所含脂肪的质量是:克,
故答案为:;
设这份快餐中所含矿物质的质量为克,则所含蛋白质的质量是克,
由题意可得:,
解得,
所含碳水化合物的质量为,
当时,取得最大值,
故答案为:.
根据脂肪所占的百分比为,可以计算出快餐中所含脂肪的质量;
根据这份快餐中蛋白质和碳水化合物所占百分比的和不高于,可以列出相应的不等式,然后即可求得所含碳水化合物质量的最大值.
本题考查一元一次不等式的应用,解答本题的关键是明确题意,列出相应的不等式.
19.【答案】
【解析】解:,
得:,
得:,即;
故答案为:,;
方程组的解是,
方程组的解为,
解得:.
故答案案为:.
方程组两方程相减求出的值,相加求出的值即可;
把看作,看作,求出方程组的解即可.
此题考查了二元一次方程组的解,二元一次方程的解,以及解二元一次方程组,弄清题中的整体代入法是解本题的关键.
20.【答案】解:
;
的平方根是,的立方根是,
,,
解得:,,
,
的平方根是.
【解析】先化简各式,然后再进行计算即可解答;
根据平方根与立方根的意义可得,,从而可得,,然后把,的值代入式子中进行计算,即可解答.
本题考查了实数的运算,平方根,立方根,准确熟练地进行计算是解题的关键.
21.【答案】解:由题意,当时,,
.
,
,.
由得,,
若,
.
.
满足题意的最大整数值为
【解析】依据题意,将代入整式,结合,进而可以得解;
依据题意,由建立不等式,进而可以得解.
本题主要考查了代数式求值,解题时要熟练掌握并准确计算.
22.【答案】解:平分,且,
,
,
;
,,
,
平分,
,
.
【解析】由角平分线的定义得的度数,根据三角形内角和定理可得答案;
由三角形外角的性质可得的度数,再根据角平分线的定义得的度数,根据三角形内角和定理可得答案.
此题考查的是对顶角、邻补角、角平分线的定义,掌握其概念是解决此题的关键.
23.【答案】解:,
答:本次调查的样本容量是;
人,
答:选择“游泳”活动的人数是人;
“跑步”活动人数为:人,
补全条形统计图如下:
人,
答:估计全校名学生中喜欢这项活动的大约有人.
【解析】用“踢毽”的人数除以所占百分比可得样本容量;
用样本容量乘“游泳”活动所占百分比可得答案;
用样本容量减去其他四种活动的人数,可得“跑步”活动人数,即可补全条形统计图;
用乘样本中“跑步”活动所占百分比即可.
本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
24.【答案】解:、如图所示:
.
理由:,
,
,
,
,
.
【解析】此题主要考查了基本作图以及平行线的性质等知识,根据题意作出正确图形是解题关键.
根据题意直接作出;
过点利用三角尺作出;
利用平行线的性质,进而得出直线与的位置关系.
25.【答案】解:如图所示:
由图可知:超市到少年宫的距离为:;
由坐标系可知:超市图书馆,公园,
公园、图书馆、超市在第一、三象限的角平分线上
同意小华的说法;
公园与图书馆的直线距离约为,
公园在图书馆的西南方向;
由图可知:影院,学校,少年宫,广场,
这四个位置在示意图上围成的四边形面积为:.
【解析】根据题意构造平面直角坐标系可求解;
由两点间的距离公式计算可求解;
先求出超市、图书馆、公园的坐标,根据坐标可求解;
利用长方形的面积减去三个三角形的面积可求解.
本题主要考查平面直角坐标系,方向角,掌握平面直角坐标系的知识是解题的关键.
26.【答案】解:设种童衣每件进价是元,种童衣每件进价是元,
根据题意得:,
解得:.
答:种童衣每件进价是元,种童衣每件进价是元;
根据题意得:
元.
答:销售完这批童衣的销售利润为元;
设购进件种童衣,则购进件种童衣,
根据题意得:,
解得:,
又为正整数,
的最大值为,此时销售完这批童衣的销售利润为元.
答:购进种童衣最多为件,此时销售完这批童衣的销售利润为元.
【解析】设种童衣每件进价是元,种童衣每件进价是元,根据“种童衣件,种童衣件,进价总额为元;种童衣件,种童衣件,进价总额为元”,可列出关于,的二元一次方程组,解之即可得出结论;
利用销售总利润每件种童衣的销售利润购进种童衣的数量每件种童衣的销售利润购进种童衣的数量,即可求出结论;
设购进件种童衣,则购进件种童衣,根据购进的种童衣不少于种童衣的倍,可列出关于的一元一次不等式,解之可求出的取值范围,取其中的最大整数值,即可得出最多购进种童衣的数量,再利用销售总利润每件种童衣的销售利润购进种童衣的数量每件种童衣的销售利润购进种童衣的数量,可求出此时销售完这批童衣的销售利润.
本题考查了二元一次方程组的应用、一元一次不等式的应用以及有理数的混合运算,解题的关键是:找准等量关系,正确列出二元一次方程组;根据各数量之间的关系,列式计算;根据各数量之间的关系,正确列出一元一次不等式.
第1页,共1页
一、选择题(本大题共16小题,共42.0分。在每小题列出的选项中,选出符合题目的一项)
1. 以下调查中,最适合采用全面调查的是( )
A. 检测神舟飞船零部件质量情况 B. 了解河北中小学生课外阅读情况
C. 调查某批次牛奶的质量 D. 中央电视台开学第一课的收视率
2. 下列各式计算正确的是( )
A. B. C. D.
3. 如图,直线,被直线所截,下列条件不能判定直线的是( )
A.
B.
C.
D.
4. 若,则点在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
5. 如果,那么下列不等式正确的是( )
A. B. C. D.
6. 已知二元一次方程的一个解是,则的值为( )
A. B. C. D.
7. 用加减消元法解二元一次方程组时,下列方法中无法消元的是( )
A. B. C. D.
8. 不等式组的解集,在数轴上表示正确的是( )
A. B.
C. D.
9. 某天课间操时,嘉嘉、淇淇、小高的位置如图所示,嘉嘉对小高说:“如果我的位置用表示,淇淇的位置用表示,那么你的位置可以表示成什么?”( )
A. B. C. D.
10. 若与互为相反数,且,则的立方根是( )
A. B. C. D.
11. 如图,同一平面内经过直线外一点的四条直线中,与直线相交的直线至少有( )
A. 条 B. 条 C. D. 条
12. 已知是不等式的解,而不是的解,则( )
A. B. C. D.
13. 某单位为响应政府号召,为“创城工作”贡献力量,需要购买分类垃圾桶个,市场上有型和型两种分类垃圾桶,型分类垃圾桶元个,型分类垃圾桶元个,总费用不超过元,则不同的购买方式有( )
A. 种 B. 种 C. 种 D. 种
14. 如图所示,嘉琪骑自行车自处沿正东方向前进,到达处后,行驶方向改为南偏东,行驶到处仍按正东方向行驶,则在处嘉琪向左拐弯的角度是( )
A. B. C. D.
15. 为了了解参加某运动会的名运动员的年龄情况,从中抽取了名运动员的年龄,就这个问题来说,下面说法正确的是( )
A. 名运动员是总体 B. 名运动员是所抽取的一个样本
C. 样本容量为名 D. 抽取的名运动员的年龄是样本
16. 我国古代数学名著九章算术中有一道题,原文是:“今有善行者行一百步,不善行者行六十步今不善行者先行一百步,善行者追之,问几何步及之?”意思是:同样时间段内,走路快的人能走步,走路慢的人只能走步走路慢的人先走步,随后走路快的人出发去追他,那么走路快的人走多少步才能追上走路慢的人?设走路快的人走步才能追上走路慢的人,此时走路慢的人走了步,则正确的方程组是( )
A. B. C. D.
二、填空题(本大题共3小题,共9.0分)
17. 在,,,,,,,,中是无理数的个数有______ 个.
18. 某营养快餐的成分为:蛋白质、脂肪、矿物质、碳水化合物其中脂肪所占的百分比为,所含蛋白质质量是矿物质质量的倍,若这种快餐总质量是克,则:
快餐中所含脂肪的质量是______ 克;
若这份快餐中蛋白质和碳水化合物所占百分比的和不高于,则所含碳水化合物最多有______ 克
19. 阅读感悟:有些关于方程组的问题,欲求的结果不是每一个未知数的值,而是关于未知数的式子的值,如以下问题:
已知实数、满足,,求和的值.
本题常规思路是将两式联立组成方程组,解得、的值再代入欲求值的整式得到答案,常规思路运算量比较大其实,仔细观察两个方程未知数的系数之间的关系,本题还可以通过适当变形整体求得整式的值,如由可得,由可得这样的解题思想就是通常所说的“整体思想”利用上面的知识解答下列问题:
已知、满足方程组,则的值为______ ,的值为______ ;
已知方程组的解是,则方程组的解是______ .
三、解答题(本大题共7小题,共69.0分。解答应写出文字说明,证明过程或演算步骤)
20. 本小题分
计算:;
已知的平方根是,的立方根是,求的平方根.
21. 本小题分
已知整式,当时,.
若,求、的值;
在的条件下,若,直接写出的最大整数值.
22. 本小题分
如图,直线与相交于点,直线与直线相交于点,且平分,且,.
求的度数;
若平分,求的度数.
23. 本小题分
为了丰富校园生活,推进校园服务,某中学在课后延时服务中,开展了一系列体育活动,为了调查哪项活动最受学生欢迎,中学团委对七年级学生进行了问卷调查,针对该项调查结果制作的两个统计图不完整,如图.
本次调查的样本容量是多少?
选择“游泳”活动的人数是多少?
通过计算补全条形统计图;
调查中,哪项活动最受学生欢迎,估计全校名学生中喜欢这项活动的有多少人?
24. 本小题分
如图,已知点在直线外,请用三角板与直尺画图,并回答第题:
过作直线,使;
过作直线,使,垂足为;
请判断直线与的位置关系,并说明理由.
25. 本小题分
小红和小兰对着如图示意图,描述了超市的位置图中小正方形的边长代表,两人的说法都是正确的:
小红:超市的坐标是;
小兰:超市在图书馆东北方向约处.
按小红和小兰所说,在图中建立平面直角坐标系,标出原点和坐标轴;
写出超市到少年宫的距离;
小华说:“公园、图书馆、超市在同一条直线上”,你同意他的说法吗?如果公园与图书馆的直线距离约为,请写出公园相对于图书馆的位置;
写出影院、学校、少年宫、广场的位置坐标,并计算这四个位置在示意图上围成的四边形面积.
26. 本小题分
某服装店欲一次性购进、两种童衣共件进行销售其中种童衣件,种童衣件,进价总额为元;种童衣件,种童衣件,进价总额为元,种童衣每件售价元,种童衣每件售价元.
求两种童衣的每件进价分别是多少元?
若每种童衣各购进件,求销售完这批童衣的销售利润;
由于资金等因素限制,实际购进的种童衣不少于种童衣的倍,那么购进种童衣最多为多少件?并求此时销售完这批童衣的销售利润.
答案和解析
1.【答案】
【解析】解:检测神舟飞船零部件质量情况,适合全面调查,故本选项符合题意;
B.了解河北中小学生课外阅读情况,适合抽样调查,故本选项不符合题意;
C.调查某批次牛奶的质量,适合抽样调查,故本选项不符合题意;
D.中央电视台开学第一课的收视率,适合抽样调查,故本选项不符合题意.
故选:.
根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似解答.
本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
2.【答案】
【解析】解:,因此选项A不符合题意;
B.,因此选项B符合题意;
C.,因此选项C不符合题意;
D.,因此选项D不符合题意;
故选:.
根据立方根,二次根式的性质和化简逐项进行计算即可.
本题考查二次根式的性质,立方根,理解立方根的定义,掌握二次根式的性质是正确解答的前提.
3.【答案】
【解析】解:由,不能判定,
故A符合题意;
,,
,
,
,
,
故B不符合题意;
,,
,
,
故C不符合题意;
,
,
故D不符合题意;
故选:.
根据平行线的判定定理判断求解即可.
此题考查了平行线的判定,熟记平行线的判定定理是解题的关键.
4.【答案】
【解析】解:,,,
,,
即,,
在第四象限,
故选:.
根据绝对值、偶次幂的非负性求出、的值,确定点的坐标,再根据直角坐标系中点的坐标与位置的关系进行解答即可.
本题考查绝对值、偶次方的非负性以及平面直角坐标系,理解绝对值、偶次方的非负性以及点的坐标特征是正确解答的前提.
5.【答案】
【解析】解:,
,
选项A符合题意;
,
,
选项B不符合题意;
,
,
选项C不符合题意;
,
,
选项D不符合题意.
故选:.
根据,应用不等式的性质,逐项判断即可.
此题主要考查了不等式的基本性质:不等式的两边同时加上或减去同一个数或同一个含有字母的式子,不等号的方向不变;不等式的两边同时乘或除以同一个正数,不等号的方向不变;不等式的两边同时乘或除以同一个负数,不等号的方向改变.
6.【答案】
【解析】解:把代入,得
,
,
.
故选:.
把代入,然后解关于的方程即可.
本题考查了求二元一次方程的解,能使二元一次方程左右两边相等的未知数的值叫做二元一次方程的解.
7.【答案】
【解析】解:用加减消元法解二元一次方程组时,
消去;消去;消去;消去,
则无法消元.
故选:.
利用加减消元法判断即可.
此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.
8.【答案】
【解析】解:,
解不等式得:;
解不等式得:;
不等式组的解集为,
数轴上表示为:
故选:.
解出每个不等式的解集,再求公共解集,把解集表示在数轴上即可.
本题考查解一元一次不等式组,解题的关键是掌握求公共解集的方法.
9.【答案】
【解析】解:如图所示:淇淇的位置用表示,
小高的位置为:.
故选:.
根据淇淇的位置用确定平面直角坐标系,然后确定小高的位置坐标.
此题主要考查了坐标确定位置,利用原点的位置得出是解题关键.
10.【答案】
【解析】解:由题意得,
,
,
,
,
,
,
,
的立方根是.
故选:.
由题意得,根据等式的性质,加上再减去,消去,得出的值,再得出的值,进行求解.
此题考查了有理数的相反数和有理数乘法的运用能力,关键是能准确理解并运用以上知识进行正确地计算.
11.【答案】
【解析】解:过直线外一点,有且只有一条直线与已知直线平行,
过直线外一点的四条直线中,最多只有一条直线与平行,
与直线相交的直线至少有条,
故选:.
由平行公理,即可判断.
本题考查平行公理,关键是掌握平行公理.
12.【答案】
【解析】解:是不等式的解,
,
解得,
不是的解,
,
解得,
,
故选:.
求出,,即可得.
本题考查解一元一次不等式,解题的关键是掌握一元一次不等式的解的定义.
13.【答案】
【解析】解:设购买个型分类垃圾桶,则购买个型分类垃圾桶,
根据题意得:,
解得:,
又,均为自然数,
可以为,,,,,
共有种不同的购买方案.
故选:.
设购买个型分类垃圾桶,则购买个型分类垃圾桶,利用总价单价数量,结合总价不超过元,可列出关于的一元一次不等式,解之可得出的取值范围,再结合,均为自然数,即可得出共有种不同的购买方案.
本题考查了一元一次不等式的应用,根据各数量之间的关系,正确列出一元一次不等式是解题的关键.
14.【答案】
【解析】解:如图,嘉琪行驶到处仍按正东方向行驶,即方向行驶,
嘉琪骑自行车自处沿正东方向前进,到达处后,行驶方向改为南偏东,
,
,
,
即在处嘉琪向左拐弯的角度是,
故选:.
根据“两直线平行,同位角相等”求解即可.
此题考查了平行线的性质,熟记平行线的性质定理是解题的关键.
15.【答案】
【解析】解:、名运动员的年龄是总体,原说法错误,故本选项错误;
B、名运动员的年龄是所抽取的一个样本,原说法错误,故本选项错误;
C、样本容量为,原说法错误,故本选项错误;
D、抽取的名运动员的年龄是样本,说法正确,故本选项正确;
故选D.
总体:我们把所要考察的对象的全体叫做总体;
个体:把组成总体的每一个考察对象叫做个体;
样本:从总体中取出的一部分个体叫做这个总体的一个样本;
样本容量:一个样本包括的个体数量叫做样本容量.
结合选项进行判断即可.
本题考查了总体、样本及样本容量的知识,属于基础题,掌握基本定义是关键.
16.【答案】
【解析】解:由题意得:
,
故选:.
根据“同样时间段内,走路快的人能走步,走路慢的人只能走步”和“走路慢的人先走步,”列方程组求解.
本题考查了二元一次方程组的应用,找到线相等关系是解题的关键.
17.【答案】
【解析】
【分析】
本题主要考查的是无理数的认识,掌握无理数常见类型是解题的关键.无理数常见的三种类型开不尽的方根,;特定结构的无限不循环小数,如两个之间依次多一个;含有的绝大部分数,如.
【解答】
解:是有理数,是一个有限小数,是有理数,是无理数,是有理数,是无理数,是有理数,是有理数,是有理数,是无理数.
故答案为.
18.【答案】
【解析】解:由题意可得,
快餐中所含脂肪的质量是:克,
故答案为:;
设这份快餐中所含矿物质的质量为克,则所含蛋白质的质量是克,
由题意可得:,
解得,
所含碳水化合物的质量为,
当时,取得最大值,
故答案为:.
根据脂肪所占的百分比为,可以计算出快餐中所含脂肪的质量;
根据这份快餐中蛋白质和碳水化合物所占百分比的和不高于,可以列出相应的不等式,然后即可求得所含碳水化合物质量的最大值.
本题考查一元一次不等式的应用,解答本题的关键是明确题意,列出相应的不等式.
19.【答案】
【解析】解:,
得:,
得:,即;
故答案为:,;
方程组的解是,
方程组的解为,
解得:.
故答案案为:.
方程组两方程相减求出的值,相加求出的值即可;
把看作,看作,求出方程组的解即可.
此题考查了二元一次方程组的解,二元一次方程的解,以及解二元一次方程组,弄清题中的整体代入法是解本题的关键.
20.【答案】解:
;
的平方根是,的立方根是,
,,
解得:,,
,
的平方根是.
【解析】先化简各式,然后再进行计算即可解答;
根据平方根与立方根的意义可得,,从而可得,,然后把,的值代入式子中进行计算,即可解答.
本题考查了实数的运算,平方根,立方根,准确熟练地进行计算是解题的关键.
21.【答案】解:由题意,当时,,
.
,
,.
由得,,
若,
.
.
满足题意的最大整数值为
【解析】依据题意,将代入整式,结合,进而可以得解;
依据题意,由建立不等式,进而可以得解.
本题主要考查了代数式求值,解题时要熟练掌握并准确计算.
22.【答案】解:平分,且,
,
,
;
,,
,
平分,
,
.
【解析】由角平分线的定义得的度数,根据三角形内角和定理可得答案;
由三角形外角的性质可得的度数,再根据角平分线的定义得的度数,根据三角形内角和定理可得答案.
此题考查的是对顶角、邻补角、角平分线的定义,掌握其概念是解决此题的关键.
23.【答案】解:,
答:本次调查的样本容量是;
人,
答:选择“游泳”活动的人数是人;
“跑步”活动人数为:人,
补全条形统计图如下:
人,
答:估计全校名学生中喜欢这项活动的大约有人.
【解析】用“踢毽”的人数除以所占百分比可得样本容量;
用样本容量乘“游泳”活动所占百分比可得答案;
用样本容量减去其他四种活动的人数,可得“跑步”活动人数,即可补全条形统计图;
用乘样本中“跑步”活动所占百分比即可.
本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
24.【答案】解:、如图所示:
.
理由:,
,
,
,
,
.
【解析】此题主要考查了基本作图以及平行线的性质等知识,根据题意作出正确图形是解题关键.
根据题意直接作出;
过点利用三角尺作出;
利用平行线的性质,进而得出直线与的位置关系.
25.【答案】解:如图所示:
由图可知:超市到少年宫的距离为:;
由坐标系可知:超市图书馆,公园,
公园、图书馆、超市在第一、三象限的角平分线上
同意小华的说法;
公园与图书馆的直线距离约为,
公园在图书馆的西南方向;
由图可知:影院,学校,少年宫,广场,
这四个位置在示意图上围成的四边形面积为:.
【解析】根据题意构造平面直角坐标系可求解;
由两点间的距离公式计算可求解;
先求出超市、图书馆、公园的坐标,根据坐标可求解;
利用长方形的面积减去三个三角形的面积可求解.
本题主要考查平面直角坐标系,方向角,掌握平面直角坐标系的知识是解题的关键.
26.【答案】解:设种童衣每件进价是元,种童衣每件进价是元,
根据题意得:,
解得:.
答:种童衣每件进价是元,种童衣每件进价是元;
根据题意得:
元.
答:销售完这批童衣的销售利润为元;
设购进件种童衣,则购进件种童衣,
根据题意得:,
解得:,
又为正整数,
的最大值为,此时销售完这批童衣的销售利润为元.
答:购进种童衣最多为件,此时销售完这批童衣的销售利润为元.
【解析】设种童衣每件进价是元,种童衣每件进价是元,根据“种童衣件,种童衣件,进价总额为元;种童衣件,种童衣件,进价总额为元”,可列出关于,的二元一次方程组,解之即可得出结论;
利用销售总利润每件种童衣的销售利润购进种童衣的数量每件种童衣的销售利润购进种童衣的数量,即可求出结论;
设购进件种童衣,则购进件种童衣,根据购进的种童衣不少于种童衣的倍,可列出关于的一元一次不等式,解之可求出的取值范围,取其中的最大整数值,即可得出最多购进种童衣的数量,再利用销售总利润每件种童衣的销售利润购进种童衣的数量每件种童衣的销售利润购进种童衣的数量,可求出此时销售完这批童衣的销售利润.
本题考查了二元一次方程组的应用、一元一次不等式的应用以及有理数的混合运算,解题的关键是:找准等量关系,正确列出二元一次方程组;根据各数量之间的关系,列式计算;根据各数量之间的关系,正确列出一元一次不等式.
第1页,共1页
同课章节目录
