2023—2024学年 人教版数学八年级上册 11.1与三角形有关的线段 同步达标测试题 (含解析)
文档属性
| 名称 | 2023—2024学年 人教版数学八年级上册 11.1与三角形有关的线段 同步达标测试题 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 594.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-15 20:25:43 | ||
图片预览



文档简介
2023-2024学年人教版八年级数学上册《11.1与三角形有关的线段》
同步达标测试题(附答案)
一、单选题(满分32分)
1.下列长度的各组线段能组成一个三角形的是( )
A. B.
C. D.
2.如果三角形的两边长分别为2和5,那么这个三角形的周长可能是( )
A.10 B.12 C.14 D.16
3.已知三角形三边长分别为3,a,7,且a为奇数,则这样的三角形有( )
A.2个 B.3个 C.4个 D.5个
4.下列说法正确的个数有( )
① 三角形的角平分线、中线和高都在三角形内
② 直角三角形只有一条高
③ 三角形的高至少有一条在三角形内
④ 三角形的高是直线,角平分线是射线,中线是线段
A.1个 B.2个 C.3个 D.4个
5.如图,是中线,,.若的周长为10,则的周长为( )
A.8 B.9 C.10 D.11
6.如图所示,AD、BF、CE分别是的三条高线,则下列的面积表述正确的是( )
A. B. C. D.
7.如图,是的中线,是的中线, 于点F,且,则面积是( )
A.3 B.4 C.6 D.12
8.如图,,,分别是的高,角平分线、中线,则下列各式中错误的是( )
A. B. C. D.
二、填空题(满分40分)
9.一个三角形的两边长分别是4和7,如果第三边长为整数,那么第三边可取的最大整数是__________.
10.己知a,b,c是的三条边长,化简的结果为__________.
11.如图,已知的面积为25,,在直线上有一动点P,连接点C、P,则线段的最小值为:______.
12.若三角形三边长分别为,则的取值范围是__________.
13.已知为的高,若,则______.
14.如图所示,在中,已知点,,分别是,,的中点,且,则的值为_____________.
15.如图,在中,是中线,是角平分线,是高.填空:
(1)___________;
(2)____________;
(3)______;
(4)______.
16.要使五边形木架(用5根木条钉成)不变形,至少要再钉_____根木条.
三、解答题(满分48分)
17.已知一个三角形的第一条边长为,第二条边长为
(1)求第三条边长的取值范围;(用含,的式子表示)
(2)若,满足,第三条边长为整数,求这个三角形周长的最大值
18.如图,在中,为边上的高,点为边上的一点,连接.
(1)当为边上的中线时,若,的面积为24,求的长;
(2)当为的角平分线时,若,,求的度数.
19.三角形如图,的边上的高为,中线为边上的高为,已知,,.
(1)求的面积;
(2)求的长;
(3)和的面积有何关系?
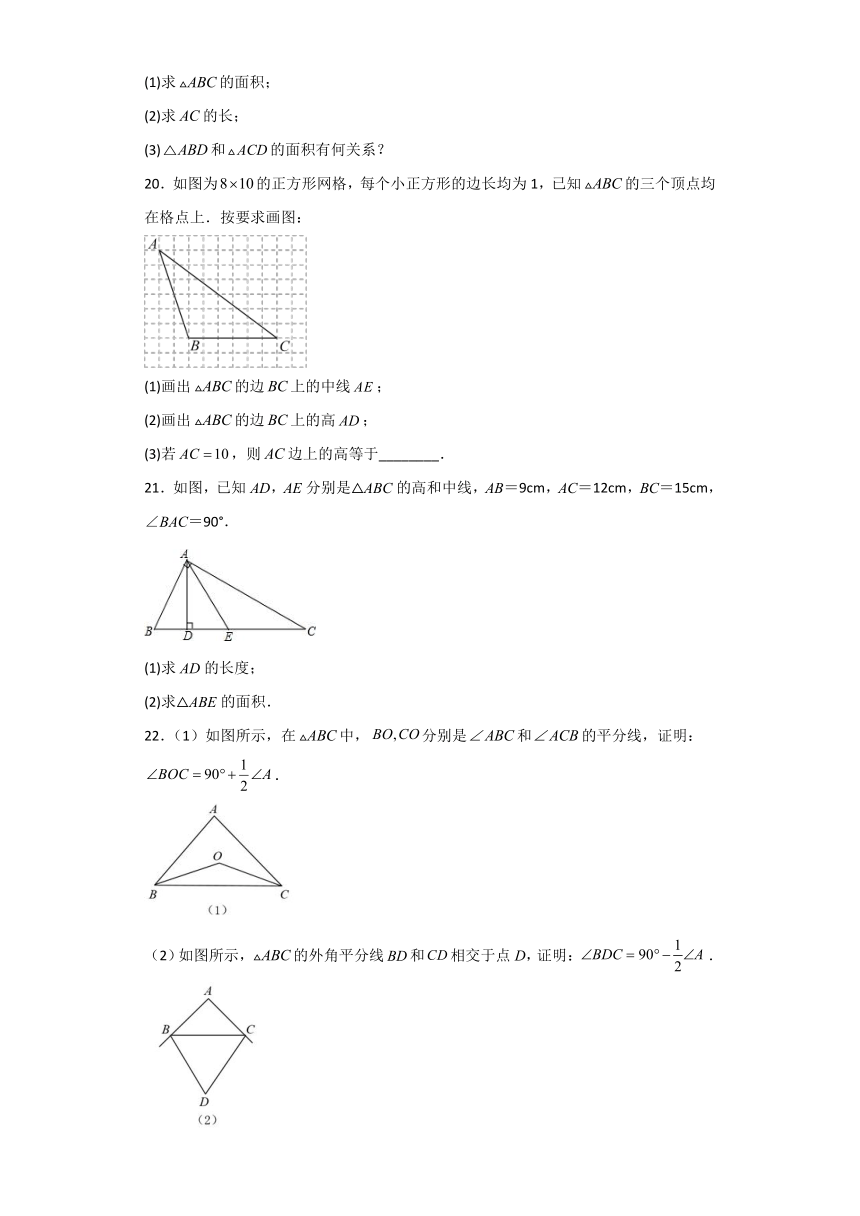
20.如图为的正方形网格,每个小正方形的边长均为1,已知的三个顶点均在格点上.按要求画图:
(1)画出的边上的中线;
(2)画出的边上的高;
(3)若,则边上的高等于________.
21.如图,已知AD,AE分别是△ABC的高和中线,AB=9cm,AC=12cm,BC=15cm,∠BAC=90°.
(1)求AD的长度;
(2)求△ABE的面积.
22.(1)如图所示,在中,分别是和的平分线,证明:.
(2)如图所示,的外角平分线和相交于点D,证明:.
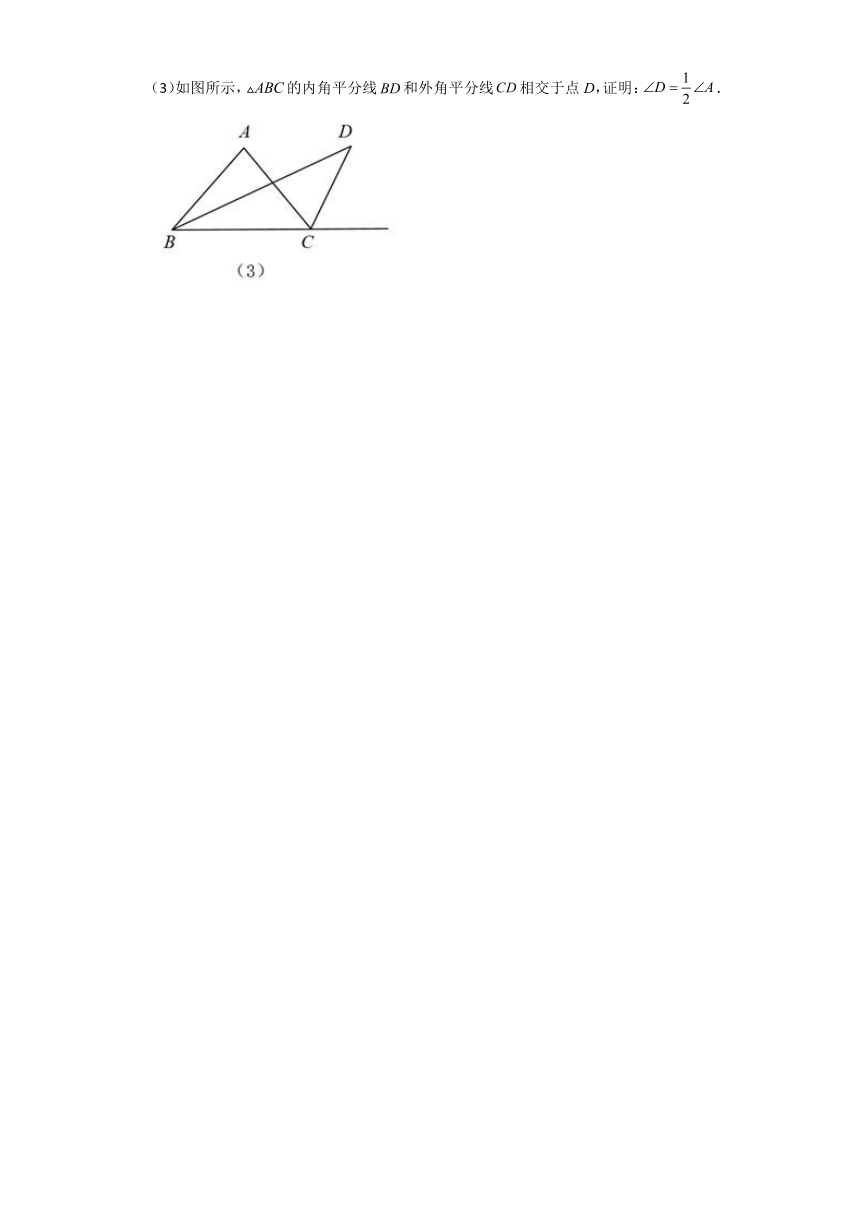
(3)如图所示,的内角平分线和外角平分线相交于点D,证明:.
参考答案
1.解:A.,不符合题意;
B.,不符合题意;
C.,不符合题意;
D.,符合题意,
故选D.
2.解:∵三角形的两边长为2和5,
∴第三边x的长度范围是,即,
∴这个三角形的周长a范围是,即,故B正确.
故选:B.
3.解:∵三角形三边长分别为3,a,7,
,
∴,
∵a为奇数,
∴a可取5,7,9
∴这样的三角形共3个,故B正确.
故选:B.
4.解:①钝角三角形的三条高两条在三角形外,故错误;
②直角三角形有三条高,故错误;
③ 三角形的高至少有一条在三角形内,故正确;
④三角形的高,角平分线及中线都是线段,故错误;
故选A.
5.解:∵是中线,
∴,
∵的周长为10,,
∴,
∴,
∴的周长为,
故选:D.
6.解:、BF、CE分别是的三条高线,
求的面积正确的公式是.
故选:B.
7.解:∵,
∴,
∵是的中线,
∴,
∴.
∵是的中线,
∴.
故选:C.
8.解:∵C,,分别是的高、角平分线、中线,
∴,,,无法确定.
故选:C.
9.解:设第三边为a,
根据三角形的三边关系,得:,
即,
∵a为整数,
∴a的最大值为10;
故答案为:10.
10.解:∵a,b,c是的三条边长,
∴,,
∴
;
故答案为:.
11.解:∵点到直线,垂线段最短,
∴当时,线段的值最小,
此时:的面积为,
∵,
∴;
故答案为:5.
12.解:由题意,,
解得:,
故答案为:.
13.解:①当点在线段上时,
∵,
∴;
②当点在延长线上时,
则:;
综上:6或14;
故答案为:6或14.
14.解:点是的中点,
,,
点是的中点,
,,
.
点是的中点,
.
故答案为:.
15. 解:(1)∵是中线,
∴;
故答案为,;
(2)∵是角平分线,
∴,
故答案为,;
(3)∵是高,
∴,
故答案为;
(4)由题意得:;
故答案为.
16.解:如图,再钉上两根木条,就可以使五边形分成三个三角形.故至少要再钉两根木条,
故答案为:2.
17.(1)解:∵三角形的第一条边长为,第二条边长为,
∴第三条边长的取值范围是,
即,
∴第三条边长的取值范围是;
(2)∵,满足,第三条边长为整数,
∴,
∴,
∴,即,
则三角形的周长为:,
∵为整数,
∴可取最大值为,
此时这个三角形周长的最大值为,
∴这个三角形周长的最大值为.
18.(1)解:是边上的高,,的面积为24,
,
为边上的中线,
是的中点,
.
(2)解:为边的高,
,.
.
为的角平分线,
,
.
19.(1)解:的面积;
(2)∵的面积,,
∴;
(3)∵为的中线,
∴,
∵的边上的高为,
∴.
即:和的面积相等.
20.(1)解:如图所示,即为所求;
(2)解:如图所示,即为所求;
(3)解:设边上的高为h,
∵,
∴,
∴边上的高等于,
故答案为:.
21.(1)解:在中,,是边上的高,
,,,
根据可得
;
(2)解:在中,是边上的中线,且,
,
在中,是边上的高,且由(1)知,
.
22.解:(1)设.
由的内角和为,得.①
由的内角和为,得.②
由②得.③
把③代入①,得,
即,
即
(2)∵BD、CD为△ABC两外角∠ABC、∠ACB的平分线,
∴
由三角形内角和定理得,,
=180°-[∠A+(∠A+∠ABC+∠ACB)],
=180°-(∠A+180°),
=90°-∠A;
(3)如图:
∵BD为△ABC的角平分线,交AC与点E,CD为△ABC外角∠ACE的平分线,两角平分线交于点D
∴∠1=∠2,∠5=(∠A+2∠1),∠3=∠4,
在△ABE中,∠A=180°-∠1-∠3
∴∠1+∠3=180°-∠A①
在△CDE中,∠D=180°-∠4-∠5=180°-∠3-(∠A+2∠1),
即2∠D=360°-2∠3-∠A-2∠1=360°-2(∠1+∠3)-∠A②,
把①代入②得∠D=∠A.
同步达标测试题(附答案)
一、单选题(满分32分)
1.下列长度的各组线段能组成一个三角形的是( )
A. B.
C. D.
2.如果三角形的两边长分别为2和5,那么这个三角形的周长可能是( )
A.10 B.12 C.14 D.16
3.已知三角形三边长分别为3,a,7,且a为奇数,则这样的三角形有( )
A.2个 B.3个 C.4个 D.5个
4.下列说法正确的个数有( )
① 三角形的角平分线、中线和高都在三角形内
② 直角三角形只有一条高
③ 三角形的高至少有一条在三角形内
④ 三角形的高是直线,角平分线是射线,中线是线段
A.1个 B.2个 C.3个 D.4个
5.如图,是中线,,.若的周长为10,则的周长为( )
A.8 B.9 C.10 D.11
6.如图所示,AD、BF、CE分别是的三条高线,则下列的面积表述正确的是( )
A. B. C. D.
7.如图,是的中线,是的中线, 于点F,且,则面积是( )
A.3 B.4 C.6 D.12
8.如图,,,分别是的高,角平分线、中线,则下列各式中错误的是( )
A. B. C. D.
二、填空题(满分40分)
9.一个三角形的两边长分别是4和7,如果第三边长为整数,那么第三边可取的最大整数是__________.
10.己知a,b,c是的三条边长,化简的结果为__________.
11.如图,已知的面积为25,,在直线上有一动点P,连接点C、P,则线段的最小值为:______.
12.若三角形三边长分别为,则的取值范围是__________.
13.已知为的高,若,则______.
14.如图所示,在中,已知点,,分别是,,的中点,且,则的值为_____________.
15.如图,在中,是中线,是角平分线,是高.填空:
(1)___________;
(2)____________;
(3)______;
(4)______.
16.要使五边形木架(用5根木条钉成)不变形,至少要再钉_____根木条.
三、解答题(满分48分)
17.已知一个三角形的第一条边长为,第二条边长为
(1)求第三条边长的取值范围;(用含,的式子表示)
(2)若,满足,第三条边长为整数,求这个三角形周长的最大值
18.如图,在中,为边上的高,点为边上的一点,连接.
(1)当为边上的中线时,若,的面积为24,求的长;
(2)当为的角平分线时,若,,求的度数.
19.三角形如图,的边上的高为,中线为边上的高为,已知,,.
(1)求的面积;
(2)求的长;
(3)和的面积有何关系?
20.如图为的正方形网格,每个小正方形的边长均为1,已知的三个顶点均在格点上.按要求画图:
(1)画出的边上的中线;
(2)画出的边上的高;
(3)若,则边上的高等于________.
21.如图,已知AD,AE分别是△ABC的高和中线,AB=9cm,AC=12cm,BC=15cm,∠BAC=90°.
(1)求AD的长度;
(2)求△ABE的面积.
22.(1)如图所示,在中,分别是和的平分线,证明:.
(2)如图所示,的外角平分线和相交于点D,证明:.
(3)如图所示,的内角平分线和外角平分线相交于点D,证明:.
参考答案
1.解:A.,不符合题意;
B.,不符合题意;
C.,不符合题意;
D.,符合题意,
故选D.
2.解:∵三角形的两边长为2和5,
∴第三边x的长度范围是,即,
∴这个三角形的周长a范围是,即,故B正确.
故选:B.
3.解:∵三角形三边长分别为3,a,7,
,
∴,
∵a为奇数,
∴a可取5,7,9
∴这样的三角形共3个,故B正确.
故选:B.
4.解:①钝角三角形的三条高两条在三角形外,故错误;
②直角三角形有三条高,故错误;
③ 三角形的高至少有一条在三角形内,故正确;
④三角形的高,角平分线及中线都是线段,故错误;
故选A.
5.解:∵是中线,
∴,
∵的周长为10,,
∴,
∴,
∴的周长为,
故选:D.
6.解:、BF、CE分别是的三条高线,
求的面积正确的公式是.
故选:B.
7.解:∵,
∴,
∵是的中线,
∴,
∴.
∵是的中线,
∴.
故选:C.
8.解:∵C,,分别是的高、角平分线、中线,
∴,,,无法确定.
故选:C.
9.解:设第三边为a,
根据三角形的三边关系,得:,
即,
∵a为整数,
∴a的最大值为10;
故答案为:10.
10.解:∵a,b,c是的三条边长,
∴,,
∴
;
故答案为:.
11.解:∵点到直线,垂线段最短,
∴当时,线段的值最小,
此时:的面积为,
∵,
∴;
故答案为:5.
12.解:由题意,,
解得:,
故答案为:.
13.解:①当点在线段上时,
∵,
∴;
②当点在延长线上时,
则:;
综上:6或14;
故答案为:6或14.
14.解:点是的中点,
,,
点是的中点,
,,
.
点是的中点,
.
故答案为:.
15. 解:(1)∵是中线,
∴;
故答案为,;
(2)∵是角平分线,
∴,
故答案为,;
(3)∵是高,
∴,
故答案为;
(4)由题意得:;
故答案为.
16.解:如图,再钉上两根木条,就可以使五边形分成三个三角形.故至少要再钉两根木条,
故答案为:2.
17.(1)解:∵三角形的第一条边长为,第二条边长为,
∴第三条边长的取值范围是,
即,
∴第三条边长的取值范围是;
(2)∵,满足,第三条边长为整数,
∴,
∴,
∴,即,
则三角形的周长为:,
∵为整数,
∴可取最大值为,
此时这个三角形周长的最大值为,
∴这个三角形周长的最大值为.
18.(1)解:是边上的高,,的面积为24,
,
为边上的中线,
是的中点,
.
(2)解:为边的高,
,.
.
为的角平分线,
,
.
19.(1)解:的面积;
(2)∵的面积,,
∴;
(3)∵为的中线,
∴,
∵的边上的高为,
∴.
即:和的面积相等.
20.(1)解:如图所示,即为所求;
(2)解:如图所示,即为所求;
(3)解:设边上的高为h,
∵,
∴,
∴边上的高等于,
故答案为:.
21.(1)解:在中,,是边上的高,
,,,
根据可得
;
(2)解:在中,是边上的中线,且,
,
在中,是边上的高,且由(1)知,
.
22.解:(1)设.
由的内角和为,得.①
由的内角和为,得.②
由②得.③
把③代入①,得,
即,
即
(2)∵BD、CD为△ABC两外角∠ABC、∠ACB的平分线,
∴
由三角形内角和定理得,,
=180°-[∠A+(∠A+∠ABC+∠ACB)],
=180°-(∠A+180°),
=90°-∠A;
(3)如图:
∵BD为△ABC的角平分线,交AC与点E,CD为△ABC外角∠ACE的平分线,两角平分线交于点D
∴∠1=∠2,∠5=(∠A+2∠1),∠3=∠4,
在△ABE中,∠A=180°-∠1-∠3
∴∠1+∠3=180°-∠A①
在△CDE中,∠D=180°-∠4-∠5=180°-∠3-(∠A+2∠1),
即2∠D=360°-2∠3-∠A-2∠1=360°-2(∠1+∠3)-∠A②,
把①代入②得∠D=∠A.
