2023—2024学年 人教版数学八年级上册 第11章三角形 同步达标测试题 (含解析)
文档属性
| 名称 | 2023—2024学年 人教版数学八年级上册 第11章三角形 同步达标测试题 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 462.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-15 20:34:10 | ||
图片预览


文档简介
2023-2024学年人教版八年级数学上册《第11章三角形》同步达标测试题(附答案)
一、单选题(满分32分)
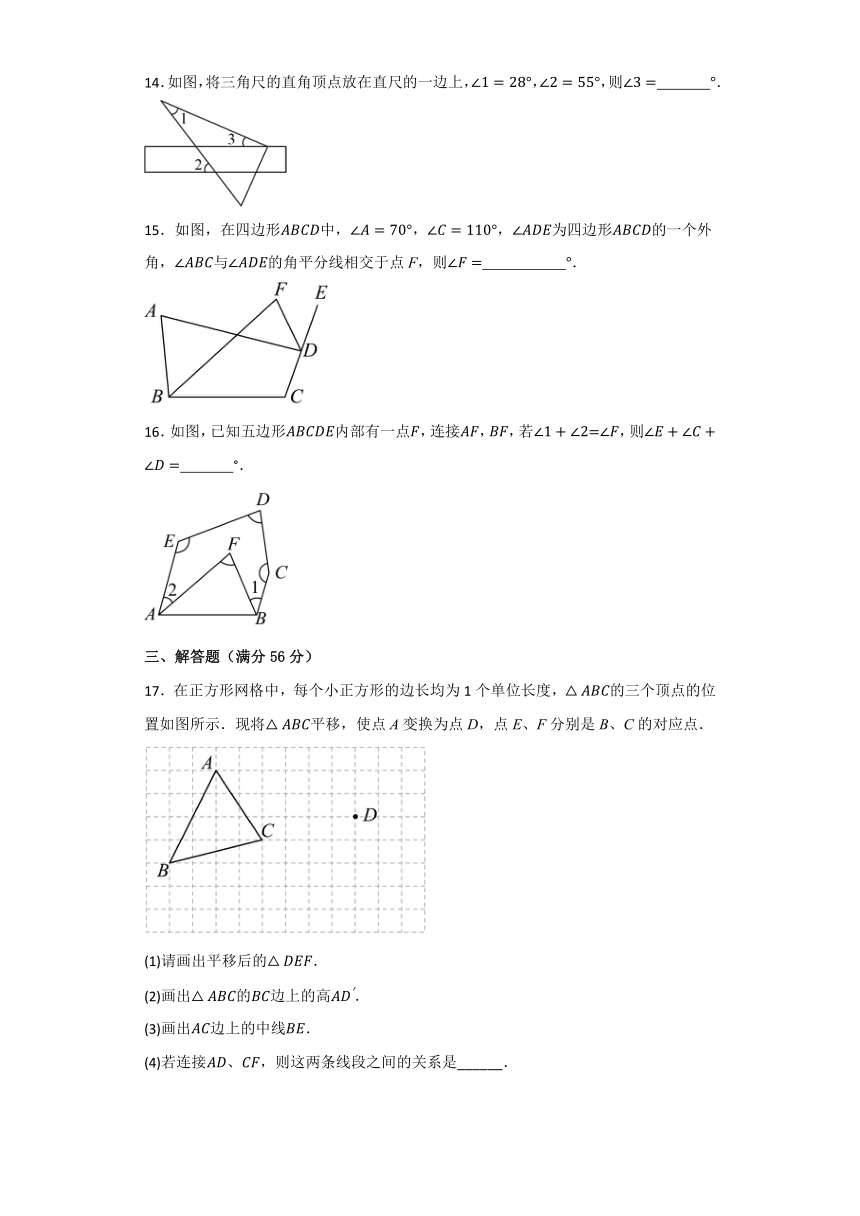
1.下列长度的三条线段能组成三角形的是( )
A.1cm,2cm,3cm B.2cm,3cm,5.5cm
C.5cm,8cm,12cm D.4cm,5cm,9cm
2.如图,在中,的度数是( )
A. B. C. D.
3.下列四个图中,正确画出中边上的高是( )
A. B.
C. D.
4.在一个多边形中,小于的内角最多有( )个.
A.2 B.3 C.4 D.5
5.如图,在中,点是边中点,点是中线的中点.若的面积是,则的面积是( )
A. B. C. D.
6.下列多边形中,内角和为的图形是( )
A.六边形 B.七边形 C.八边形 D.九边形
7.如图,在中,,将点A与点B分别沿和折叠,使点A、B与点C重合,则的度数为( )
A. B. C. D.
8.如图,已知,点、分别在、边上,将沿折叠,点落在外部的点处,此时测得,则的度数为( )
A. B. C. D.
二、填空题(满分32分)
9.一个三角形的两边长分别为3和8,且第三边长为奇数,则这个三角形的周长是 .
10.正八边形的内角和等于 °.
11.若一个多边形的内角和是外角和的3倍,则这个多边形的边数是 ,这个多边形对角线有 条.
12.如图,已知是的边上的中线,若,的周长比的周长多,则 .
13.如图,在中,已知,,垂足分别为D,E,,,,则 .
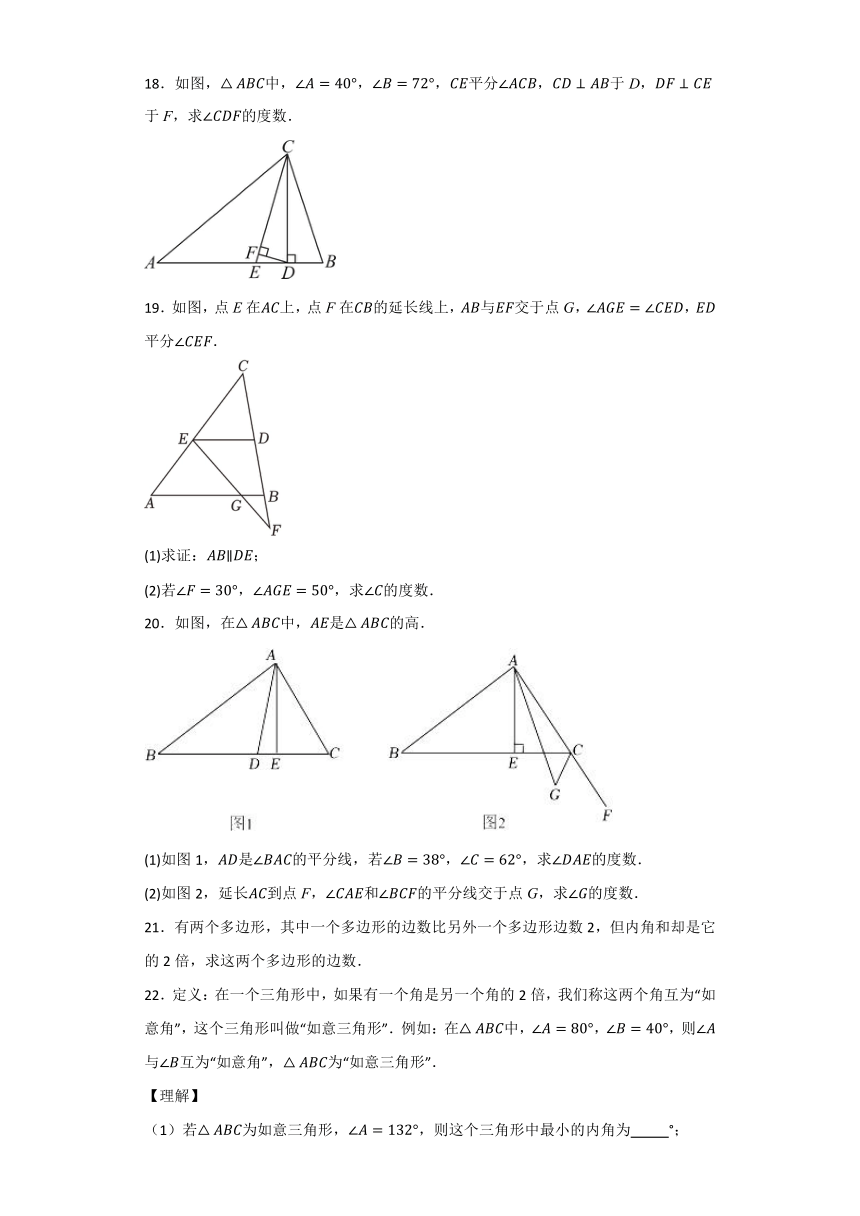
14.如图,将三角尺的直角顶点放在直尺的一边上,,,则 .
15.如图,在四边形中,,为四边形的一个外角,与的角平分线相交于点F,则 .
16.如图,已知五边形内部有一点,连接,,若,则 °.
三、解答题(满分56分)
17.在正方形网格中,每个小正方形的边长均为1个单位长度,的三个顶点的位置如图所示.现将平移,使点A变换为点D,点E、F分别是B、C的对应点.
(1)请画出平移后的.
(2)画出的边上的高.
(3)画出边上的中线.
(4)若连接、,则这两条线段之间的关系是______.
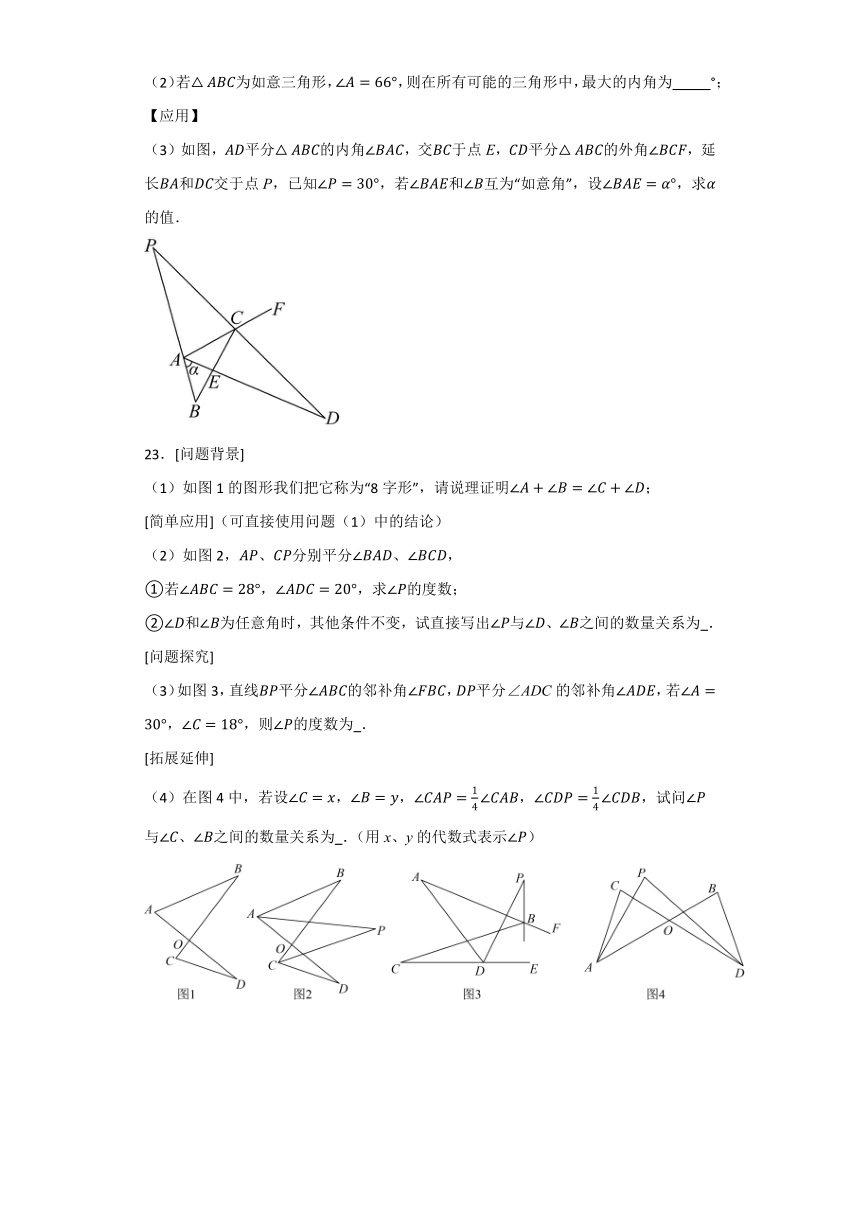
18.如图,中,,平分,于D,于F,求的度数.
19.如图,点E在上,点F在的延长线上,与交于点G,,平分.
(1)求证:;
(2)若,求的度数.
20.如图,在中,是的高.
(1)如图1,是的平分线,若,,求的度数.
(2)如图2,延长到点F,和的平分线交于点G,求的度数.
21.有两个多边形,其中一个多边形的边数比另外一个多边形边数2,但内角和却是它的2倍,求这两个多边形的边数.
22.定义:在一个三角形中,如果有一个角是另一个角的2倍,我们称这两个角互为“如意角”,这个三角形叫做“如意三角形”.例如:在中,,,则与互为“如意角”,为“如意三角形”.
【理解】
(1)若为如意三角形,,则这个三角形中最小的内角为 °;
(2)若为如意三角形,,则在所有可能的三角形中,最大的内角为 °;
【应用】
(3)如图,平分的内角,交于点E,平分的外角,延长和交于点P,已知,若和互为“如意角”,设,求的值.
23.[问题背景]
(1)如图1的图形我们把它称为“8字形”,请说理证明;
[简单应用](可直接使用问题(1)中的结论)
(2)如图2,、分别平分、,
①若,,求的度数;
②和为任意角时,其他条件不变,试直接写出与、之间的数量关系为 .
[问题探究]
(3)如图3,直线平分的邻补角,平分∠ADC的邻补角,若,,则的度数为 .
[拓展延伸]
(4)在图4中,若设,,,,试问与、之间的数量关系为 .(用x、y的代数式表示)
参考答案
1.解:根据三角形任意两边的和大于第三边,得
A中, 1+2=3, 不能组成三角形;
B中, 3+2=5<5.5, 不能够组成三角形;
C中, 5+8=13>12, 能组成三角形;
D中, 4+5=9, 不能组成三角形.
故选: C.
2.解:,
,
,
.
故选:C.
3.解:根据三角形高线的定义,边上的高是过点A向作垂线,垂足为D,
纵观各图形,选项A、B、D都不符合题意,只有选项C符合题意,
故选:C.
4.解:由于多边形的内角小于,
所以这个多边形的外角要大于,
而多边形的外角和为,
所以内角的个数小于个,
∴最多有4个,
故选:C.
5.解:点是线段的中点,
,
的面积是,
,
点是边中点,
,
的面积是.
故选:B.
6.解:设这个多边形的边数为n,
则,
解得:,
∴这个多边形是八边形;
故选C
7.解:因为,点A与点B分别沿和折叠,使点A、B与点C重合,
所以,
因为,
所以,
解得.
故选:C.
8.解:由折叠性质知,,,
,
,
,
,
,
故选:D.
9.解:设这个三角形的第三边长为x,
∵一个三角形的两边长分别是3和8,
∴,即,
又∵第三边的长为奇数,
∴第三边的长或,
当时,这个三角形的周长为,
当时,这个三角形的周长,
故答案为:18或20.
10.解:,
故答案为:.
11.解:①设这个多边形的边数为n.
根据题意得:180°×(n﹣2)=360°×3,
解得:n=8;
②这个多边形对角线有:(条),
故答案为:8;20.
12.解:∵是中边上的中线,
∴,
∴和的周长的差,
∵,
∴.
故答案为:5.
13.解:∵,,,
∴,
∵,,
∴,
∴,
∴.
故答案为:.
14.解:如图,
,
,
又,
,
故答案为:27.
15.解:∵四边形的内角和为,而,
∴,
又∵,
∴,
∵是的平分线,是的平分线,
∴,
又∵,
∴,
故答案为:70.
16.解:∵五边形的内角和为:,
∴,
∵,,
∴,
∴,
故答案为:.
17.(1)解:如图,即为所求;
(2)如图,即为所求;
(3)如图,即为所求;
(4)由平移的性质可得:与平行且相等.
18.解:∵中,,
∴,
∵平分,
∴,
∴,
∵,即,
∴,
∵,即,
∴.
19.(1)证明:∵平分,
∴,
∵,
∴,
∴;
(2)解:∵,
∴,
∵平分,
∴,
∵,,
∴.
20.(1)解:∵,
∴,
∵是的平分线,
∴,
∵是的高,
∴,
∵,
∴,
∴;
(2)∵和的平分线交于点G,,
∴,
∵,
∴,
即,
∵是的高,
∴,
∴.
21.解:设边数少的一个多边形的边数为,则另一个多边形的边数为;
根据题意:,
解得:,则.
22.解:(1)为如意三角形,
必有两个角互为“如意角”,
当时,
,
此时,
(舍去),不符合实际;
同理,当时, (舍去),不符合实际;
当时,
,
,
,
,
同理,当时, ,
综上所述:这个三角形中最小的内角为,
故答案为:;
解:(2)为如意三角形,
必有两个角互为“如意角”,
当时,
,
此时,
;
同理,当时, ;
此时,这个这个三角形中最大的内角为;
当时,
,
,
,
,
同理,当时, ,
此时,这个这个三角形中最大的内角为;
综上所述:这个三角形中最大的内角为或,
故答案为:或;
解:(3) 平分的内角,平分的外角,
,,
,,
,
,
,
,
,
和互为“如意角”, 即和互为“如意角”,
或,
或(舍去),
,
,
.
23.解:(1)如图1中,
∵,,,
∴;
(2)①如图2中,
设,,
则有,
∴,
∴,
∴;
②由①得:;
(3)如图3中,设,,
则有,,
∴,
∴;
故答案为:;
(4)如图4中,设,,则,,
则有,
∴ ,
∴,
故答案为:.
一、单选题(满分32分)
1.下列长度的三条线段能组成三角形的是( )
A.1cm,2cm,3cm B.2cm,3cm,5.5cm
C.5cm,8cm,12cm D.4cm,5cm,9cm
2.如图,在中,的度数是( )
A. B. C. D.
3.下列四个图中,正确画出中边上的高是( )
A. B.
C. D.
4.在一个多边形中,小于的内角最多有( )个.
A.2 B.3 C.4 D.5
5.如图,在中,点是边中点,点是中线的中点.若的面积是,则的面积是( )
A. B. C. D.
6.下列多边形中,内角和为的图形是( )
A.六边形 B.七边形 C.八边形 D.九边形
7.如图,在中,,将点A与点B分别沿和折叠,使点A、B与点C重合,则的度数为( )
A. B. C. D.
8.如图,已知,点、分别在、边上,将沿折叠,点落在外部的点处,此时测得,则的度数为( )
A. B. C. D.
二、填空题(满分32分)
9.一个三角形的两边长分别为3和8,且第三边长为奇数,则这个三角形的周长是 .
10.正八边形的内角和等于 °.
11.若一个多边形的内角和是外角和的3倍,则这个多边形的边数是 ,这个多边形对角线有 条.
12.如图,已知是的边上的中线,若,的周长比的周长多,则 .
13.如图,在中,已知,,垂足分别为D,E,,,,则 .
14.如图,将三角尺的直角顶点放在直尺的一边上,,,则 .
15.如图,在四边形中,,为四边形的一个外角,与的角平分线相交于点F,则 .
16.如图,已知五边形内部有一点,连接,,若,则 °.
三、解答题(满分56分)
17.在正方形网格中,每个小正方形的边长均为1个单位长度,的三个顶点的位置如图所示.现将平移,使点A变换为点D,点E、F分别是B、C的对应点.
(1)请画出平移后的.
(2)画出的边上的高.
(3)画出边上的中线.
(4)若连接、,则这两条线段之间的关系是______.
18.如图,中,,平分,于D,于F,求的度数.
19.如图,点E在上,点F在的延长线上,与交于点G,,平分.
(1)求证:;
(2)若,求的度数.
20.如图,在中,是的高.
(1)如图1,是的平分线,若,,求的度数.
(2)如图2,延长到点F,和的平分线交于点G,求的度数.
21.有两个多边形,其中一个多边形的边数比另外一个多边形边数2,但内角和却是它的2倍,求这两个多边形的边数.
22.定义:在一个三角形中,如果有一个角是另一个角的2倍,我们称这两个角互为“如意角”,这个三角形叫做“如意三角形”.例如:在中,,,则与互为“如意角”,为“如意三角形”.
【理解】
(1)若为如意三角形,,则这个三角形中最小的内角为 °;
(2)若为如意三角形,,则在所有可能的三角形中,最大的内角为 °;
【应用】
(3)如图,平分的内角,交于点E,平分的外角,延长和交于点P,已知,若和互为“如意角”,设,求的值.
23.[问题背景]
(1)如图1的图形我们把它称为“8字形”,请说理证明;
[简单应用](可直接使用问题(1)中的结论)
(2)如图2,、分别平分、,
①若,,求的度数;
②和为任意角时,其他条件不变,试直接写出与、之间的数量关系为 .
[问题探究]
(3)如图3,直线平分的邻补角,平分∠ADC的邻补角,若,,则的度数为 .
[拓展延伸]
(4)在图4中,若设,,,,试问与、之间的数量关系为 .(用x、y的代数式表示)
参考答案
1.解:根据三角形任意两边的和大于第三边,得
A中, 1+2=3, 不能组成三角形;
B中, 3+2=5<5.5, 不能够组成三角形;
C中, 5+8=13>12, 能组成三角形;
D中, 4+5=9, 不能组成三角形.
故选: C.
2.解:,
,
,
.
故选:C.
3.解:根据三角形高线的定义,边上的高是过点A向作垂线,垂足为D,
纵观各图形,选项A、B、D都不符合题意,只有选项C符合题意,
故选:C.
4.解:由于多边形的内角小于,
所以这个多边形的外角要大于,
而多边形的外角和为,
所以内角的个数小于个,
∴最多有4个,
故选:C.
5.解:点是线段的中点,
,
的面积是,
,
点是边中点,
,
的面积是.
故选:B.
6.解:设这个多边形的边数为n,
则,
解得:,
∴这个多边形是八边形;
故选C
7.解:因为,点A与点B分别沿和折叠,使点A、B与点C重合,
所以,
因为,
所以,
解得.
故选:C.
8.解:由折叠性质知,,,
,
,
,
,
,
故选:D.
9.解:设这个三角形的第三边长为x,
∵一个三角形的两边长分别是3和8,
∴,即,
又∵第三边的长为奇数,
∴第三边的长或,
当时,这个三角形的周长为,
当时,这个三角形的周长,
故答案为:18或20.
10.解:,
故答案为:.
11.解:①设这个多边形的边数为n.
根据题意得:180°×(n﹣2)=360°×3,
解得:n=8;
②这个多边形对角线有:(条),
故答案为:8;20.
12.解:∵是中边上的中线,
∴,
∴和的周长的差,
∵,
∴.
故答案为:5.
13.解:∵,,,
∴,
∵,,
∴,
∴,
∴.
故答案为:.
14.解:如图,
,
,
又,
,
故答案为:27.
15.解:∵四边形的内角和为,而,
∴,
又∵,
∴,
∵是的平分线,是的平分线,
∴,
又∵,
∴,
故答案为:70.
16.解:∵五边形的内角和为:,
∴,
∵,,
∴,
∴,
故答案为:.
17.(1)解:如图,即为所求;
(2)如图,即为所求;
(3)如图,即为所求;
(4)由平移的性质可得:与平行且相等.
18.解:∵中,,
∴,
∵平分,
∴,
∴,
∵,即,
∴,
∵,即,
∴.
19.(1)证明:∵平分,
∴,
∵,
∴,
∴;
(2)解:∵,
∴,
∵平分,
∴,
∵,,
∴.
20.(1)解:∵,
∴,
∵是的平分线,
∴,
∵是的高,
∴,
∵,
∴,
∴;
(2)∵和的平分线交于点G,,
∴,
∵,
∴,
即,
∵是的高,
∴,
∴.
21.解:设边数少的一个多边形的边数为,则另一个多边形的边数为;
根据题意:,
解得:,则.
22.解:(1)为如意三角形,
必有两个角互为“如意角”,
当时,
,
此时,
(舍去),不符合实际;
同理,当时, (舍去),不符合实际;
当时,
,
,
,
,
同理,当时, ,
综上所述:这个三角形中最小的内角为,
故答案为:;
解:(2)为如意三角形,
必有两个角互为“如意角”,
当时,
,
此时,
;
同理,当时, ;
此时,这个这个三角形中最大的内角为;
当时,
,
,
,
,
同理,当时, ,
此时,这个这个三角形中最大的内角为;
综上所述:这个三角形中最大的内角为或,
故答案为:或;
解:(3) 平分的内角,平分的外角,
,,
,,
,
,
,
,
,
和互为“如意角”, 即和互为“如意角”,
或,
或(舍去),
,
,
.
23.解:(1)如图1中,
∵,,,
∴;
(2)①如图2中,
设,,
则有,
∴,
∴,
∴;
②由①得:;
(3)如图3中,设,,
则有,,
∴,
∴;
故答案为:;
(4)如图4中,设,,则,,
则有,
∴ ,
∴,
故答案为:.
