2023—2024学年鲁教版(五四制)九年级数学上册 第1章 反比例函数单元备课
文档属性
| 名称 | 2023—2024学年鲁教版(五四制)九年级数学上册 第1章 反比例函数单元备课 |

|
|
| 格式 | docx | ||
| 文件大小 | 313.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-15 00:00:00 | ||
图片预览




文档简介
课题 第一章反比例函数 总第 课时 课型 新授课
时间
新课标 要 求 (1)领会反比例函数的意义,理解反比例函数的概念。 (2)能根据实际问题中的条件确定反比例函数的关系式。 (3)掌握反比例函数的图象的性质。
教 学 目 标 1.理解并掌握反比例函数的概念 经历抽象反比例函数概念的过程,领会反比例函数的意义,理解反比例函数的概念. 3.能够列出实际问题中反比例函数的表达式
重点 理解并掌握反比例函数的概念,能够列出实际问题中反比例函数的表达式
难点 理解并掌握反比例函数的概念,能够列出实际问题中反比例函数的表达式
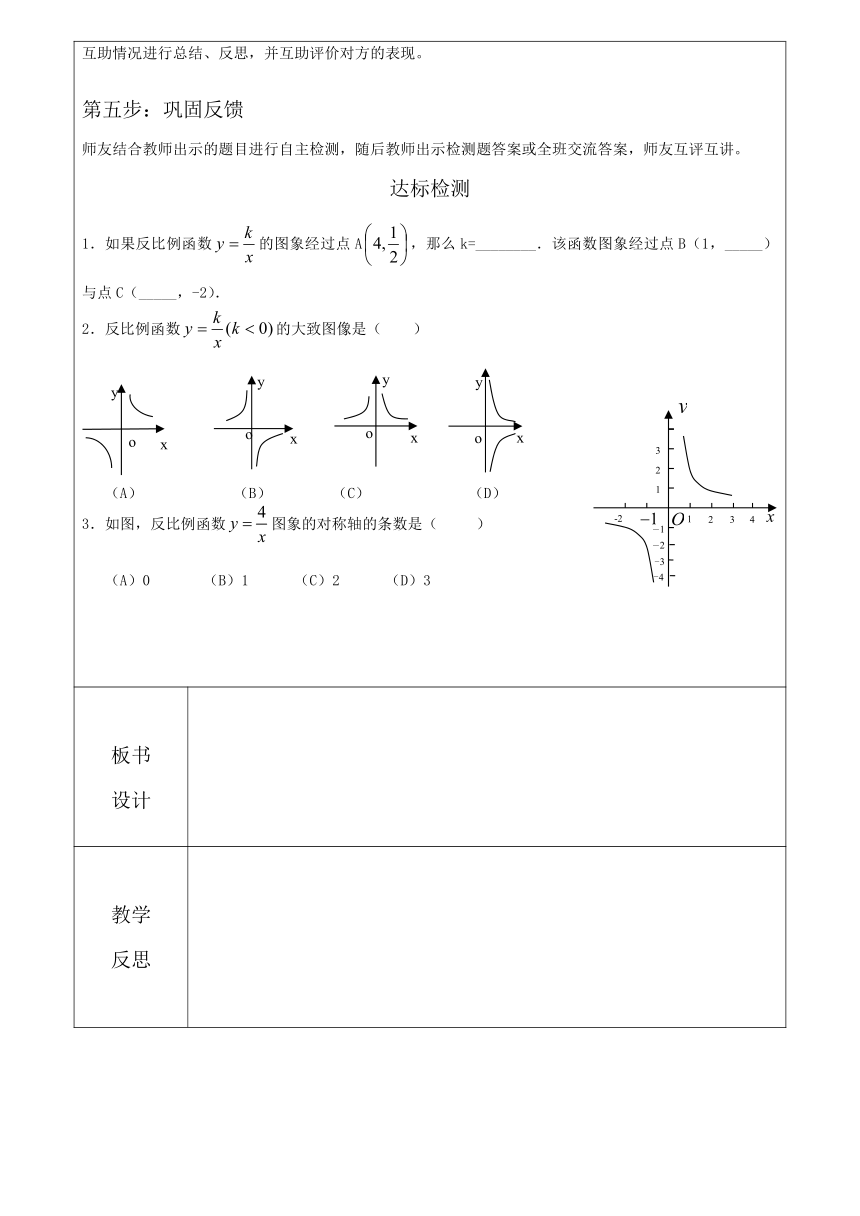
第一步:复习回顾:学生回顾所学有关的知识,并交流完成学案问题: 一次函数(正比例函数)的概念:函数y=_______ (k、b为常数,k______)叫做一次函数。 当b_____时,函数y=____ (k____)叫做正比例函数. 2.一次函数y=kx+b(k≠0)的性质: ⑴当k>0时,y随x的增大而_______;图象经过第 象限。 当k<0时,y随x的增大而_______;图象经过第 象限。 (2)两个一次函数的图象关于y轴对称,则它们的k , b 两个一次函数的图象关于x轴对称,则它们的k , b 两个一次函数的图象平行,则它们的k , b 第二步:互助探究 学习任务一:自学课本2页-3页例题以上的内容,完成下列问题: 把2页上面的三个问题完成,可以做在书上 回答议一议的问题,尝试归纳出反比例函数的定义: 小组交流对反比例函数概念的理解,并回答想一想的问题: 学习任务二:1、自学课本3页例题,并尝试写一写: 2、完成课本4页的做一做,小组交流答案,并体会反比例函数的实际意义: 自学诊断:学生先独立完成,小组交流完成情况。 1.一般地,如果两个变量、之间的关系可以表示成_________(_______,_____)的形式,那么称是的反比例函数,其中______表示自变量. 2.反比例函数的自变量的取值不能为________. 3.下列哪个等式中的y是x的反比例函数? , , , , , 第三步:分层提高 师友结合教师出示的分层次练习题进行自主练习。 1.基础训练:课本第4页随堂练习+习题1.1第1-3题。 2.提高训练:(1)课本第4页习题1.1第4、5题。 (2)当m取什么值时,函数是反比例函数? 第四步:总结归纳 引导师友交流、总结本节课的知识点、易错点、重难点、解题思路方法以及包含的数学思想,对本节课的互助情况进行总结、反思,并互助评价对方的表现。 第五步:巩固反馈 师友结合教师出示的题目进行自主检测,随后教师出示检测题答案或全班交流答案,师友互评互讲。 达标检测 1.(4分)下列关系式中的y是x的反比例函数吗?如果是,比例系数k是多少 (1) y=_____________(2)y=1-3x__________ (3)xy=1_____________ (4)y=________ 2.(2分)已知函数 y=(m-3) x|m|-4 是反比例函数,则 m = ___ 3.(4分)已知y是x的反比例函数,当x=2时,y=6 (1)写出y与x的函数关系式 (2)求当x=4时y的值
板书 设计
教学 反思
课题 1.2反比例函数的图象与性质(1) 总第 课时 课型 新授课
时间
新课标 要 求 (1)领会反比例函数的意义,理解反比例函数的概念。 (2)能根据实际问题中的条件确定反比例函数的关系式。 (3)掌握反比例函数的图象的性质。
教 学 目 标 1.进一步熟悉作函数图象的步骤,会作反比例函数的图象. 2.体会函数的三种表示方法的相互转化,对函数进行认识上的整合. 3.逐步提高从函数图象中获取信息的能力,探索并掌握反比例函数的主要性质.
重点 会画反比例函数图像,掌握反比例函数的性质.
难点 理解并掌握反比例函数性质,能解决相关问题.
第一步:复习回顾:学生回顾所学有关的知识,并交流完成学案问题 反比例函数概念: 反比例函数形式: 第二步:互助探究 在课本上画出反比例函数与的图象,回答下列问题: 1.比较两个函数图象,可以发现它们都由两支_____组成. 2.它们在坐标系中的_______不同,经过的象限是第_________象限,经过的象限是第_________象限。 【总结归纳】反比例函数具有如下性质: (1)反比例函数的图象是__________. (2)当时,图象的两个分支分别位于____________象限内; (3)当时,图象的两个分支分别位于____________象限内. (4)反比例函数的图象是轴对称图形,其对称轴为____________;反比例函数的图象也是中心对称图形,其对称中心为___________. 自学诊断:学生先独立完成,小组交流完成情况。 1.填空: (1)函数图象在第_______象限内;函数图象在第_______象限内; 2.在同一直角坐标系中,在课本上分别画出函数与的图象. 第三步:分层提高 师友结合教师出示的分层次练习题进行自主练习。 1.基础训练:课本第8页随堂练习+习题1.2第1-2题。 2.提高训练:课本第9页习题1.1第3、4题 第四步:总结归纳 引导师友交流、总结本节课的知识点、易错点、重难点、解题思路方法以及包含的数学思想,对本节课的互助情况进行总结、反思,并互助评价对方的表现。 第五步:巩固反馈 师友结合教师出示的题目进行自主检测,随后教师出示检测题答案或全班交流答案,师友互评互讲。 达标检测 如果反比例函数的图象经过点A,那么k=________.该函数图象经过点B(1,_____)与点C(_____,-2). 反比例函数的大致图像是( ) (
y
o
x
o
y
x
x
o
y
y
x
o
) (A) (B) (C) (D) 3.如图,反比例函数图象的对称轴的条数是( ) (A)0 (B)1 (C)2 (D)3
板书 设计
教学 反思
课题 1.2反比例函数图像与性质(2) 总第 课时 课型 新授课
时间
新课标 要 求 (1)领会反比例函数的意义,理解反比例函数的概念。 (2)能根据实际问题中的条件确定反比例函数的关系式。 (3)掌握反比例函数的图象的性质。
教 学 目 标 1.通过反比例函数的图象的分析,探索并掌握反比例函数的图象的性质. 2.体会数学与现实生活的紧密联系,增强应用意识,提高运用代数方法解决问题的能力.
重点 反比例函数图象性质的应用.
难点 反比例函数图象图象特征的分析及应用,学会从函数图象上分析、解决问题.
第一步:复习回顾:学生回顾所学有关的知识,并交流完成学案问题: 反比例函数具有如下性质: (1)反比例函数的图象是__________. (2)当时,图象的两个分支分别位于____________象限内; (3)当时,图象的两个分支分别位于____________象限内. (4)反比例函数的图象是轴对称图形,其对称轴为____________;反比例函数的图象也是中心对称图形,其对称中心为___________. 第二步:互助探究 学习任务一:自学课本9页-11页例题以上的内容,完成下列问题: 把10页上面的三个问题完成,可以做在书上. 回答议一议的问题,尝试归纳出反比例函数的图象与性质: 小组交流对反比例函数图像与性质进一步的理解. 学习任务二:1、自学课本11页例题,并尝试写一写: 2、完成课本11页的议一议和想一想,小组交流答案,并体会反比例函数图象与性质: 判断下列说法是否正确 (1)反比例函数图象的每个分支只能无限接近x轴和y轴,但永远也不可能到达x轴或y轴.( )(2)反比例函数图象若过点(a,b),则它一定过点(-a,-b).( ) 自学诊断:学生先独立完成,小组交流完成情况。 1.一般地,如果两个变量、之间的关系可以表示成_________(_______,_____)的形式,那么称是的反比例函数,其中______表示自变量. 2.反比例函数的自变量的取值不能为________. 3.下列哪个等式中的y是x的反比例函数? , , , , , 第三步:分层提高 师友结合教师出示的分层次练习题进行自主练习。 1.基础训练:课本第12页随堂练习+习题1.3第1-3题。 2.提高训练:(1)课本第14页习题1.3第4、5题。 (2).如图,Rt△ABO的顶点A是双曲线与直线在第二象限的交点, AB⊥轴于B且S△ABO= (1)求这两个函数的解析式 (2)求直线与双曲线的两个交点A,C的坐标和△AOC的面积。 第四步:总结归纳 引导师友交流、总结本节课的知识点、易错点、重难点、解题思路方法以及包含的数学思想,对本节课的互助情况进行总结、反思,并互助评价对方的表现。 第五步:巩固反馈 师友结合教师出示的题目进行自主检测,随后教师出示检测题答案或全班交流答案,师友互评互讲。
板书 设计
教学 反思
课题 1.3反比例函数的应用 总第 课时 课型 新授课
时间
新课标 要 求 (1)领会反比例函数的意义,理解反比例函数的概念。 (2)能根据实际问题中的条件确定反比例函数的关系式。 (3)掌握反比例函数的图象的性质。
教 学 目 标 1.能灵活运用反比例函数的知识分析、解决一些实际问题. 2.体验反比例函数式有效的描述现实世界的重要手段,认识到数学是解决实际问题的重要工具,培养“学数学,用数学”的意识.
重点 掌握从实际问题中构建反比例函数模型的方法.
难点 用反比例函数的性质解决一些简单的实际问题.
第一步:复习回顾:学生回顾所学有关的知识,并交流完成学案问题: 什么是反比例函数? 反比例函数的图象有什么性质? 第二步:互助探究 学习任务一:自学课本14页-15页例题以上的内容,完成下列问题: 把14页上题目的问题完成,可以做在书上. 小组交流对反比例函数的理解. 学习任务二:1、自学课本15页做一做,并尝试写一写: 2、小组交流答案,并体会反比例函数图象与性质: 自学诊断:学生先独立完成,小组交流完成情况。 完成16页课后随堂练习 第三步:分层提高 师友结合教师出示的分层次练习题进行自主练习。 1.基础训练:课本第16页习题1.4第1-2题。 2.提高训练:(1)课本第16页习题1.4第3题。 第四步:总结归纳 引导师友交流、总结本节课的知识点、易错点、重难点、解题思路方法以及包含的数学思想,对本节课的互助情况进行总结、反思,并互助评价对方的表现。 第五步:巩固反馈 师友结合教师出示的题目进行自主检测,随后教师出示检测题答案或全班交流答案,师友互评互讲。 达标检测 第三模块:达标测试 1.面积为2的△ABC,一边长为x,这边上的高为y,则y与x的变化规律用图象表示大致是( ) 2.在某一电路中,保持电压不变,电流I(安培)与电阻R(欧姆)成反比例,当电阻R=5欧姆时,电流I=2安培。 求I与R之间的函数关系式 (2)当电流I=0.5安培时,求电阻R的值;
板书 设计
教学 反思
课题 第一章反比例函数 复习 总第 课时 课型 新授课
时间
新课标 要 求 (1)领会反比例函数的意义,理解反比例函数的概念。 (2)能根据实际问题中的条件确定反比例函数的关系式。 (3)掌握反比例函数的图象的性质。
教 学 目 标 1、理解反比例函数概念,掌握反比例函数的主要性质。 2、通过对实际问题中数量关系的探索,掌握用函数的思想去研究其变化规律 3、结合具体情境体会和理解反比例函数的意义,并解决与它们有关的简单的实际问题
重点 掌握反比例函数的概念、图象、性质、应用。
难点 运用反比例函数的性质和图象解答综合题,要善于识别图形,获取有用的信息,灵活的运用数学思想方法。
知识回顾 知识点1:反比例函数的概念 一般地,如果两个变量、之间的关系可以表示成 (_________,________)的形式, 那么称是的反比例函数,其中______表示自变量。 另外两种形式:y=kx -1(k≠0)、k=xy(k≠0); 知识点2:反比例函数的图象和性质 1.图象特征: (1)由两条曲线组成,叫做双曲线; (2)图象的两个分支都无限接近 x、y 轴,但都不会与 x 轴和y 轴相交; (3)图象既是以原点为中心对称图形,又是轴对称图形. (4)自变量x≠0,函数y≠0. 2.图象和性质列表如下: 表达式y=(k≠0)图象k>0k<0性质图象在一、三象限图象在二、四象限每个象限内,函数y值随x的增大而减小每个象限内,函数y值随x的增大而增大
知识点三:反比例函数中图象的面积与|k|的联系 一般的,从反比例函数图像上任一点P向X轴Y轴作垂线,垂足为A,B,矩形PAOB的面积等于常数 。三角形PAO的面积等于 。三角形PBO的面积等于 。 知识点四:反比例函数的应用,利用反比例函数解决简单的实际问题 注意:在实际问题中列出函数关系式后,要注意自变量的取值范围。(取得是哪一段范围,是否能够取到端点。) 归类解析 考点一:反比例函数的概念问题 1、在下列函数中,是反比例函数的有 . (1)y=3x; (2)y=x2; (3)y=4x+5; (4)xy=2016; (5)y=2x-1; 2、已知反比例函数 ,求a的值和表达式。 考点二:求反比例函数的解析式 1、已知y 与 x 成反比例, 并且当 x = 5 时 y = -3, (1)求 y与 x 的函数关系式; (2)当x=-15时,求y的值; 考点三:反比例函数的图象与性质 1、如果反比例函数 的图象位于第二、四象限,那么m的范围为 。 2、已知一次函数y=kx-2,y随x的增大而减小,那么反比例函数y= ( ) A、当x>0时,y>0; B、在每个象限内y随x的增大而减小; C、图象在第一、三象限; D、图象在第二、四象限。 3、如图函数 在同一坐标系中的大致图象是( ) 4、如上图,P是反比例函数y= 图象上的一点,由P分别向x轴、y轴引垂线,阴影部分的面积为6,则这个反比例函数的解析式是 。 考点四:反比例函数与一次函数的综合题 如图:一次函数的图象y=ax+b与反比例函数 交于M(2,m)、 N((-1,-4)两点。(1)求反比例函数和一次函数的解析式; (2)根据图象写出反比例函数的值大于一次函数的值的x的取值范围。 已知,如图反比例函数 与一次函数y=-x+2的图象交于A、B两点。 求:(1)A、B两点的坐标; (2)ΔABC的面积。 提升训练: 基础训练:反比例函数与面积有关的问题: 1、设点P(m,n)是双曲线y= (k≠0)上任意一点,过P作x轴的垂线, 垂足为A,则: 面积性质(一): 2、过P分别作x轴、y的垂线,垂足分别为A、B。如图一,则: 面积性质(二): 3、设P(m,n)关于原点的对称点是 ,过P作x轴的垂线与过 作 y轴的垂线交于点A如图二。则: 面积性质(三): 拓展训练: 4、如图,已知反比例函数 的图象与一次函数y=kx+4的图象相交于 P、Q两点,并且P点纵坐标是6。 (1)求这个一次函数的解析式; (2)求ΔPOQ的面积。 第四步:总结归纳 引导师友交流、总结本节课的知识点、易错点、重难点、解题思路方法以及包含的数学思想,对本节课的互助情况进行总结、反思,并互助评价对方的表现。 第五步:巩固反馈 师友结合教师出示的题目进行自主检测,随后教师出示检测题答案或全班交流答案,师友互评互讲。
板书 设计
教学 反思
第一章 单元备课
教学内容 反比例函数
教材分析 用数学建摸的思想,从生活实际中通过图表法的表示将之转化为函数解析式的表达。这是一个“数学化”的过程,要让学生充分体会。并且数学化的过程是源于生活,又高于生活。定义域中的x,y的范围发生了变化。本节通过描点法画非线性函数的图象,对良好的作图习惯的养成,起着非常大的作用,同时也促进了数形结合思想的形成。为进一步研究函数的性质打下了良好的基础。自变量的范围,作图的趋势。在研究反比例函数的性质时,有条件的学校如果能够结合信息技术,让学生从动的观点来研究函数性质,可能更容易突破教学中的重点和难点。函数的对称性及面积的固定不变性.将函数的三种表示方法进行了有机的整合,阐述了数学来源于生活,有作用于生活,要学会用数学的眼光看问题。
课标要求 1、注意问题系列的连贯性和内容的一致性,引导学生分类研究,由特殊到一般,发现更具有一般性的命题,寻求一般性的解题方法。不同学生可提出不同要求标准,分别进行有针对性的启发和指导。 2、鼓励自主探索和猜测,鼓励发现和提出问题。提供充分思考和交流的时间,可以采用小组合作方式进行。 3、探索过程中注重有计划的渗透处理问题的策略和方法。 4、鼓励主动参与、积极思考,让每位学生都获得成功的体验。 5、关注学生活动过程,包括:是否能发现新问题;尝试从不同角度思考;善于归纳总结等。
教学目标 据本章的内容特点及学生的心理特征,在学法上,极力倡导了新课程的动手实践、独立探究、合作交流的学习方法。使学生经历知识的生成过程,培养他们的创新精神;注重学生的情感、态度和价值观的培养。
教学重难点 ⑴领会反比例函数的意义,理解反比例函数的概念,加深对函数概念的理解; ⑵能从实际问题中抽象出反比例关系的函数解析式。
教学安排 1.反比例函数的定义 1课时 2.反比例函数的图象和性质 2课时 3.反比例函数的应用 1课时 4.回顾与思考 2课时
测试安排 安排在第 周进行
时间
新课标 要 求 (1)领会反比例函数的意义,理解反比例函数的概念。 (2)能根据实际问题中的条件确定反比例函数的关系式。 (3)掌握反比例函数的图象的性质。
教 学 目 标 1.理解并掌握反比例函数的概念 经历抽象反比例函数概念的过程,领会反比例函数的意义,理解反比例函数的概念. 3.能够列出实际问题中反比例函数的表达式
重点 理解并掌握反比例函数的概念,能够列出实际问题中反比例函数的表达式
难点 理解并掌握反比例函数的概念,能够列出实际问题中反比例函数的表达式
第一步:复习回顾:学生回顾所学有关的知识,并交流完成学案问题: 一次函数(正比例函数)的概念:函数y=_______ (k、b为常数,k______)叫做一次函数。 当b_____时,函数y=____ (k____)叫做正比例函数. 2.一次函数y=kx+b(k≠0)的性质: ⑴当k>0时,y随x的增大而_______;图象经过第 象限。 当k<0时,y随x的增大而_______;图象经过第 象限。 (2)两个一次函数的图象关于y轴对称,则它们的k , b 两个一次函数的图象关于x轴对称,则它们的k , b 两个一次函数的图象平行,则它们的k , b 第二步:互助探究 学习任务一:自学课本2页-3页例题以上的内容,完成下列问题: 把2页上面的三个问题完成,可以做在书上 回答议一议的问题,尝试归纳出反比例函数的定义: 小组交流对反比例函数概念的理解,并回答想一想的问题: 学习任务二:1、自学课本3页例题,并尝试写一写: 2、完成课本4页的做一做,小组交流答案,并体会反比例函数的实际意义: 自学诊断:学生先独立完成,小组交流完成情况。 1.一般地,如果两个变量、之间的关系可以表示成_________(_______,_____)的形式,那么称是的反比例函数,其中______表示自变量. 2.反比例函数的自变量的取值不能为________. 3.下列哪个等式中的y是x的反比例函数? , , , , , 第三步:分层提高 师友结合教师出示的分层次练习题进行自主练习。 1.基础训练:课本第4页随堂练习+习题1.1第1-3题。 2.提高训练:(1)课本第4页习题1.1第4、5题。 (2)当m取什么值时,函数是反比例函数? 第四步:总结归纳 引导师友交流、总结本节课的知识点、易错点、重难点、解题思路方法以及包含的数学思想,对本节课的互助情况进行总结、反思,并互助评价对方的表现。 第五步:巩固反馈 师友结合教师出示的题目进行自主检测,随后教师出示检测题答案或全班交流答案,师友互评互讲。 达标检测 1.(4分)下列关系式中的y是x的反比例函数吗?如果是,比例系数k是多少 (1) y=_____________(2)y=1-3x__________ (3)xy=1_____________ (4)y=________ 2.(2分)已知函数 y=(m-3) x|m|-4 是反比例函数,则 m = ___ 3.(4分)已知y是x的反比例函数,当x=2时,y=6 (1)写出y与x的函数关系式 (2)求当x=4时y的值
板书 设计
教学 反思
课题 1.2反比例函数的图象与性质(1) 总第 课时 课型 新授课
时间
新课标 要 求 (1)领会反比例函数的意义,理解反比例函数的概念。 (2)能根据实际问题中的条件确定反比例函数的关系式。 (3)掌握反比例函数的图象的性质。
教 学 目 标 1.进一步熟悉作函数图象的步骤,会作反比例函数的图象. 2.体会函数的三种表示方法的相互转化,对函数进行认识上的整合. 3.逐步提高从函数图象中获取信息的能力,探索并掌握反比例函数的主要性质.
重点 会画反比例函数图像,掌握反比例函数的性质.
难点 理解并掌握反比例函数性质,能解决相关问题.
第一步:复习回顾:学生回顾所学有关的知识,并交流完成学案问题 反比例函数概念: 反比例函数形式: 第二步:互助探究 在课本上画出反比例函数与的图象,回答下列问题: 1.比较两个函数图象,可以发现它们都由两支_____组成. 2.它们在坐标系中的_______不同,经过的象限是第_________象限,经过的象限是第_________象限。 【总结归纳】反比例函数具有如下性质: (1)反比例函数的图象是__________. (2)当时,图象的两个分支分别位于____________象限内; (3)当时,图象的两个分支分别位于____________象限内. (4)反比例函数的图象是轴对称图形,其对称轴为____________;反比例函数的图象也是中心对称图形,其对称中心为___________. 自学诊断:学生先独立完成,小组交流完成情况。 1.填空: (1)函数图象在第_______象限内;函数图象在第_______象限内; 2.在同一直角坐标系中,在课本上分别画出函数与的图象. 第三步:分层提高 师友结合教师出示的分层次练习题进行自主练习。 1.基础训练:课本第8页随堂练习+习题1.2第1-2题。 2.提高训练:课本第9页习题1.1第3、4题 第四步:总结归纳 引导师友交流、总结本节课的知识点、易错点、重难点、解题思路方法以及包含的数学思想,对本节课的互助情况进行总结、反思,并互助评价对方的表现。 第五步:巩固反馈 师友结合教师出示的题目进行自主检测,随后教师出示检测题答案或全班交流答案,师友互评互讲。 达标检测 如果反比例函数的图象经过点A,那么k=________.该函数图象经过点B(1,_____)与点C(_____,-2). 反比例函数的大致图像是( ) (
y
o
x
o
y
x
x
o
y
y
x
o
) (A) (B) (C) (D) 3.如图,反比例函数图象的对称轴的条数是( ) (A)0 (B)1 (C)2 (D)3
板书 设计
教学 反思
课题 1.2反比例函数图像与性质(2) 总第 课时 课型 新授课
时间
新课标 要 求 (1)领会反比例函数的意义,理解反比例函数的概念。 (2)能根据实际问题中的条件确定反比例函数的关系式。 (3)掌握反比例函数的图象的性质。
教 学 目 标 1.通过反比例函数的图象的分析,探索并掌握反比例函数的图象的性质. 2.体会数学与现实生活的紧密联系,增强应用意识,提高运用代数方法解决问题的能力.
重点 反比例函数图象性质的应用.
难点 反比例函数图象图象特征的分析及应用,学会从函数图象上分析、解决问题.
第一步:复习回顾:学生回顾所学有关的知识,并交流完成学案问题: 反比例函数具有如下性质: (1)反比例函数的图象是__________. (2)当时,图象的两个分支分别位于____________象限内; (3)当时,图象的两个分支分别位于____________象限内. (4)反比例函数的图象是轴对称图形,其对称轴为____________;反比例函数的图象也是中心对称图形,其对称中心为___________. 第二步:互助探究 学习任务一:自学课本9页-11页例题以上的内容,完成下列问题: 把10页上面的三个问题完成,可以做在书上. 回答议一议的问题,尝试归纳出反比例函数的图象与性质: 小组交流对反比例函数图像与性质进一步的理解. 学习任务二:1、自学课本11页例题,并尝试写一写: 2、完成课本11页的议一议和想一想,小组交流答案,并体会反比例函数图象与性质: 判断下列说法是否正确 (1)反比例函数图象的每个分支只能无限接近x轴和y轴,但永远也不可能到达x轴或y轴.( )(2)反比例函数图象若过点(a,b),则它一定过点(-a,-b).( ) 自学诊断:学生先独立完成,小组交流完成情况。 1.一般地,如果两个变量、之间的关系可以表示成_________(_______,_____)的形式,那么称是的反比例函数,其中______表示自变量. 2.反比例函数的自变量的取值不能为________. 3.下列哪个等式中的y是x的反比例函数? , , , , , 第三步:分层提高 师友结合教师出示的分层次练习题进行自主练习。 1.基础训练:课本第12页随堂练习+习题1.3第1-3题。 2.提高训练:(1)课本第14页习题1.3第4、5题。 (2).如图,Rt△ABO的顶点A是双曲线与直线在第二象限的交点, AB⊥轴于B且S△ABO= (1)求这两个函数的解析式 (2)求直线与双曲线的两个交点A,C的坐标和△AOC的面积。 第四步:总结归纳 引导师友交流、总结本节课的知识点、易错点、重难点、解题思路方法以及包含的数学思想,对本节课的互助情况进行总结、反思,并互助评价对方的表现。 第五步:巩固反馈 师友结合教师出示的题目进行自主检测,随后教师出示检测题答案或全班交流答案,师友互评互讲。
板书 设计
教学 反思
课题 1.3反比例函数的应用 总第 课时 课型 新授课
时间
新课标 要 求 (1)领会反比例函数的意义,理解反比例函数的概念。 (2)能根据实际问题中的条件确定反比例函数的关系式。 (3)掌握反比例函数的图象的性质。
教 学 目 标 1.能灵活运用反比例函数的知识分析、解决一些实际问题. 2.体验反比例函数式有效的描述现实世界的重要手段,认识到数学是解决实际问题的重要工具,培养“学数学,用数学”的意识.
重点 掌握从实际问题中构建反比例函数模型的方法.
难点 用反比例函数的性质解决一些简单的实际问题.
第一步:复习回顾:学生回顾所学有关的知识,并交流完成学案问题: 什么是反比例函数? 反比例函数的图象有什么性质? 第二步:互助探究 学习任务一:自学课本14页-15页例题以上的内容,完成下列问题: 把14页上题目的问题完成,可以做在书上. 小组交流对反比例函数的理解. 学习任务二:1、自学课本15页做一做,并尝试写一写: 2、小组交流答案,并体会反比例函数图象与性质: 自学诊断:学生先独立完成,小组交流完成情况。 完成16页课后随堂练习 第三步:分层提高 师友结合教师出示的分层次练习题进行自主练习。 1.基础训练:课本第16页习题1.4第1-2题。 2.提高训练:(1)课本第16页习题1.4第3题。 第四步:总结归纳 引导师友交流、总结本节课的知识点、易错点、重难点、解题思路方法以及包含的数学思想,对本节课的互助情况进行总结、反思,并互助评价对方的表现。 第五步:巩固反馈 师友结合教师出示的题目进行自主检测,随后教师出示检测题答案或全班交流答案,师友互评互讲。 达标检测 第三模块:达标测试 1.面积为2的△ABC,一边长为x,这边上的高为y,则y与x的变化规律用图象表示大致是( ) 2.在某一电路中,保持电压不变,电流I(安培)与电阻R(欧姆)成反比例,当电阻R=5欧姆时,电流I=2安培。 求I与R之间的函数关系式 (2)当电流I=0.5安培时,求电阻R的值;
板书 设计
教学 反思
课题 第一章反比例函数 复习 总第 课时 课型 新授课
时间
新课标 要 求 (1)领会反比例函数的意义,理解反比例函数的概念。 (2)能根据实际问题中的条件确定反比例函数的关系式。 (3)掌握反比例函数的图象的性质。
教 学 目 标 1、理解反比例函数概念,掌握反比例函数的主要性质。 2、通过对实际问题中数量关系的探索,掌握用函数的思想去研究其变化规律 3、结合具体情境体会和理解反比例函数的意义,并解决与它们有关的简单的实际问题
重点 掌握反比例函数的概念、图象、性质、应用。
难点 运用反比例函数的性质和图象解答综合题,要善于识别图形,获取有用的信息,灵活的运用数学思想方法。
知识回顾 知识点1:反比例函数的概念 一般地,如果两个变量、之间的关系可以表示成 (_________,________)的形式, 那么称是的反比例函数,其中______表示自变量。 另外两种形式:y=kx -1(k≠0)、k=xy(k≠0); 知识点2:反比例函数的图象和性质 1.图象特征: (1)由两条曲线组成,叫做双曲线; (2)图象的两个分支都无限接近 x、y 轴,但都不会与 x 轴和y 轴相交; (3)图象既是以原点为中心对称图形,又是轴对称图形. (4)自变量x≠0,函数y≠0. 2.图象和性质列表如下: 表达式y=(k≠0)图象k>0k<0性质图象在一、三象限图象在二、四象限每个象限内,函数y值随x的增大而减小每个象限内,函数y值随x的增大而增大
知识点三:反比例函数中图象的面积与|k|的联系 一般的,从反比例函数图像上任一点P向X轴Y轴作垂线,垂足为A,B,矩形PAOB的面积等于常数 。三角形PAO的面积等于 。三角形PBO的面积等于 。 知识点四:反比例函数的应用,利用反比例函数解决简单的实际问题 注意:在实际问题中列出函数关系式后,要注意自变量的取值范围。(取得是哪一段范围,是否能够取到端点。) 归类解析 考点一:反比例函数的概念问题 1、在下列函数中,是反比例函数的有 . (1)y=3x; (2)y=x2; (3)y=4x+5; (4)xy=2016; (5)y=2x-1; 2、已知反比例函数 ,求a的值和表达式。 考点二:求反比例函数的解析式 1、已知y 与 x 成反比例, 并且当 x = 5 时 y = -3, (1)求 y与 x 的函数关系式; (2)当x=-15时,求y的值; 考点三:反比例函数的图象与性质 1、如果反比例函数 的图象位于第二、四象限,那么m的范围为 。 2、已知一次函数y=kx-2,y随x的增大而减小,那么反比例函数y= ( ) A、当x>0时,y>0; B、在每个象限内y随x的增大而减小; C、图象在第一、三象限; D、图象在第二、四象限。 3、如图函数 在同一坐标系中的大致图象是( ) 4、如上图,P是反比例函数y= 图象上的一点,由P分别向x轴、y轴引垂线,阴影部分的面积为6,则这个反比例函数的解析式是 。 考点四:反比例函数与一次函数的综合题 如图:一次函数的图象y=ax+b与反比例函数 交于M(2,m)、 N((-1,-4)两点。(1)求反比例函数和一次函数的解析式; (2)根据图象写出反比例函数的值大于一次函数的值的x的取值范围。 已知,如图反比例函数 与一次函数y=-x+2的图象交于A、B两点。 求:(1)A、B两点的坐标; (2)ΔABC的面积。 提升训练: 基础训练:反比例函数与面积有关的问题: 1、设点P(m,n)是双曲线y= (k≠0)上任意一点,过P作x轴的垂线, 垂足为A,则: 面积性质(一): 2、过P分别作x轴、y的垂线,垂足分别为A、B。如图一,则: 面积性质(二): 3、设P(m,n)关于原点的对称点是 ,过P作x轴的垂线与过 作 y轴的垂线交于点A如图二。则: 面积性质(三): 拓展训练: 4、如图,已知反比例函数 的图象与一次函数y=kx+4的图象相交于 P、Q两点,并且P点纵坐标是6。 (1)求这个一次函数的解析式; (2)求ΔPOQ的面积。 第四步:总结归纳 引导师友交流、总结本节课的知识点、易错点、重难点、解题思路方法以及包含的数学思想,对本节课的互助情况进行总结、反思,并互助评价对方的表现。 第五步:巩固反馈 师友结合教师出示的题目进行自主检测,随后教师出示检测题答案或全班交流答案,师友互评互讲。
板书 设计
教学 反思
第一章 单元备课
教学内容 反比例函数
教材分析 用数学建摸的思想,从生活实际中通过图表法的表示将之转化为函数解析式的表达。这是一个“数学化”的过程,要让学生充分体会。并且数学化的过程是源于生活,又高于生活。定义域中的x,y的范围发生了变化。本节通过描点法画非线性函数的图象,对良好的作图习惯的养成,起着非常大的作用,同时也促进了数形结合思想的形成。为进一步研究函数的性质打下了良好的基础。自变量的范围,作图的趋势。在研究反比例函数的性质时,有条件的学校如果能够结合信息技术,让学生从动的观点来研究函数性质,可能更容易突破教学中的重点和难点。函数的对称性及面积的固定不变性.将函数的三种表示方法进行了有机的整合,阐述了数学来源于生活,有作用于生活,要学会用数学的眼光看问题。
课标要求 1、注意问题系列的连贯性和内容的一致性,引导学生分类研究,由特殊到一般,发现更具有一般性的命题,寻求一般性的解题方法。不同学生可提出不同要求标准,分别进行有针对性的启发和指导。 2、鼓励自主探索和猜测,鼓励发现和提出问题。提供充分思考和交流的时间,可以采用小组合作方式进行。 3、探索过程中注重有计划的渗透处理问题的策略和方法。 4、鼓励主动参与、积极思考,让每位学生都获得成功的体验。 5、关注学生活动过程,包括:是否能发现新问题;尝试从不同角度思考;善于归纳总结等。
教学目标 据本章的内容特点及学生的心理特征,在学法上,极力倡导了新课程的动手实践、独立探究、合作交流的学习方法。使学生经历知识的生成过程,培养他们的创新精神;注重学生的情感、态度和价值观的培养。
教学重难点 ⑴领会反比例函数的意义,理解反比例函数的概念,加深对函数概念的理解; ⑵能从实际问题中抽象出反比例关系的函数解析式。
教学安排 1.反比例函数的定义 1课时 2.反比例函数的图象和性质 2课时 3.反比例函数的应用 1课时 4.回顾与思考 2课时
测试安排 安排在第 周进行
