第四章 一次函数单元练习(含解析)
文档属性
| 名称 | 第四章 一次函数单元练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 690.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-14 16:58:02 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
第四章 一次函数 单元练习 2023-2024学年北师大版八年级数学上册(含解析)
一、单选题
1.若点是x轴上的一个动点,它与x轴上表示3的点的距离是y,则y关于x的函数解析式为( )
A. B. C. D.
2.若函数的图象经过点,则的值是( )
A.4 B. C.2 D.
3.已知一次函数(k为常数,且),无论k取何值,该函数的图像总经过一个定点,则这个定点的坐标是( )
A. B. C. D.
4.下列关于函数的结论正确的是( )
A.函数图象经过点
B.函数图象经过第一、三象限
C.y随x的增大而减小
D.不论x为何值,总有
5.如图所示,一个实心铁球静止在长方体水槽的底部,现向水槽匀速注水,下列图像中能大致反映水槽中水的深度与注水时间关系的是( )
A. B.
C. D.
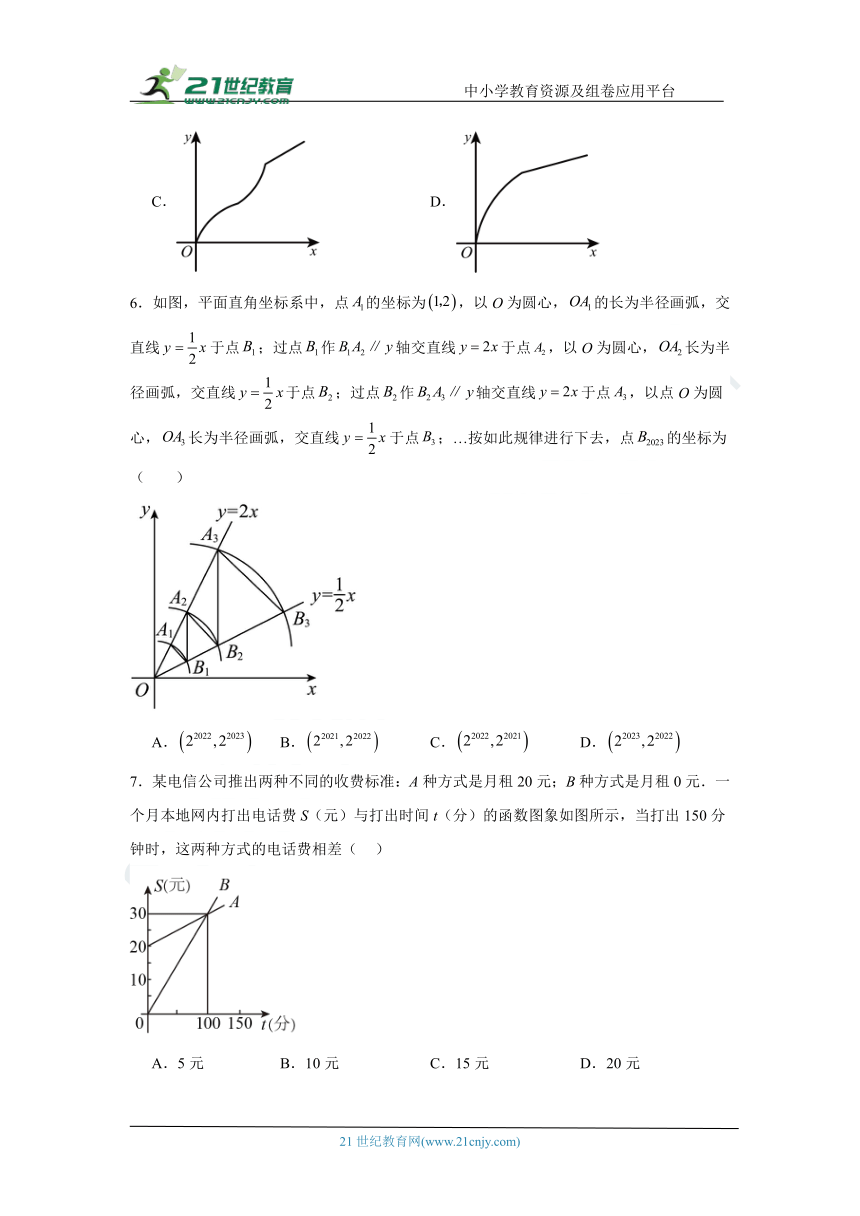
6.如图,平面直角坐标系中,点的坐标为,以O为圆心,的长为半径画弧,交直线于点;过点作轴交直线于点,以O为圆心,长为半径画弧,交直线于点;过点作轴交直线于点,以点O为圆心,长为半径画弧,交直线于点;…按如此规律进行下去,点的坐标为( )
A. B. C. D.
7.某电信公司推出两种不同的收费标准:A种方式是月租20元;B种方式是月租0元.一个月本地网内打出电话费S(元)与打出时间t(分)的函数图象如图所示,当打出150分钟时,这两种方式的电话费相差( )
A.5元 B.10元 C.15元 D.20元
二、填空题
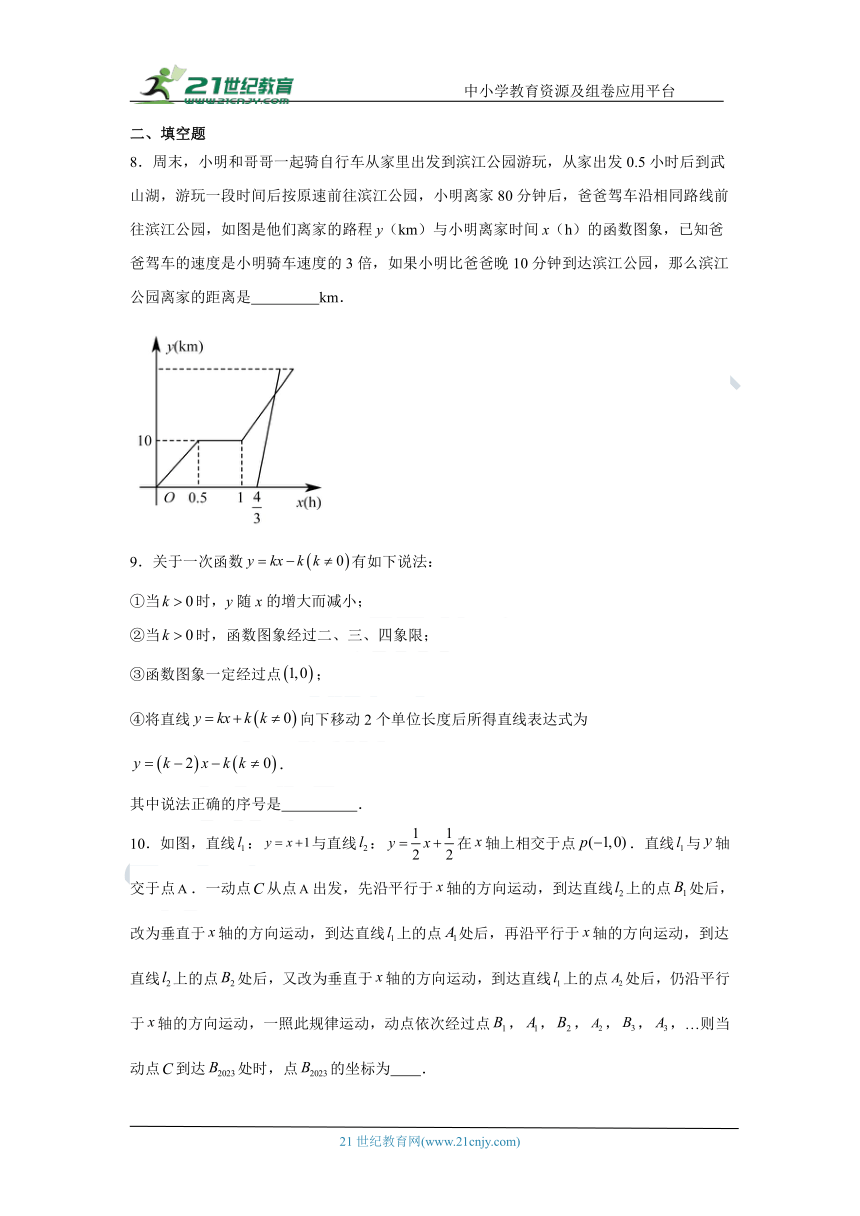
8.周末,小明和哥哥一起骑自行车从家里出发到滨江公园游玩,从家出发0.5小时后到武山湖,游玩一段时间后按原速前往滨江公园,小明离家80分钟后,爸爸驾车沿相同路线前往滨江公园,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象,已知爸爸驾车的速度是小明骑车速度的3倍,如果小明比爸爸晚10分钟到达滨江公园,那么滨江公园离家的距离是 km.
9.关于一次函数有如下说法:
①当时,y随x的增大而减小;
②当时,函数图象经过二、三、四象限;
③函数图象一定经过点;
④将直线向下移动2个单位长度后所得直线表达式为.
其中说法正确的序号是 .
10.如图,直线:与直线:在轴上相交于点.直线与轴交于点.一动点从点出发,先沿平行于轴的方向运动,到达直线上的点处后,改为垂直于轴的方向运动,到达直线上的点处后,再沿平行于轴的方向运动,到达直线上的点处后,又改为垂直于轴的方向运动,到达直线上的点处后,仍沿平行于轴的方向运动,一照此规律运动,动点依次经过点,,,,,,…则当动点到达处时,点的坐标为 .
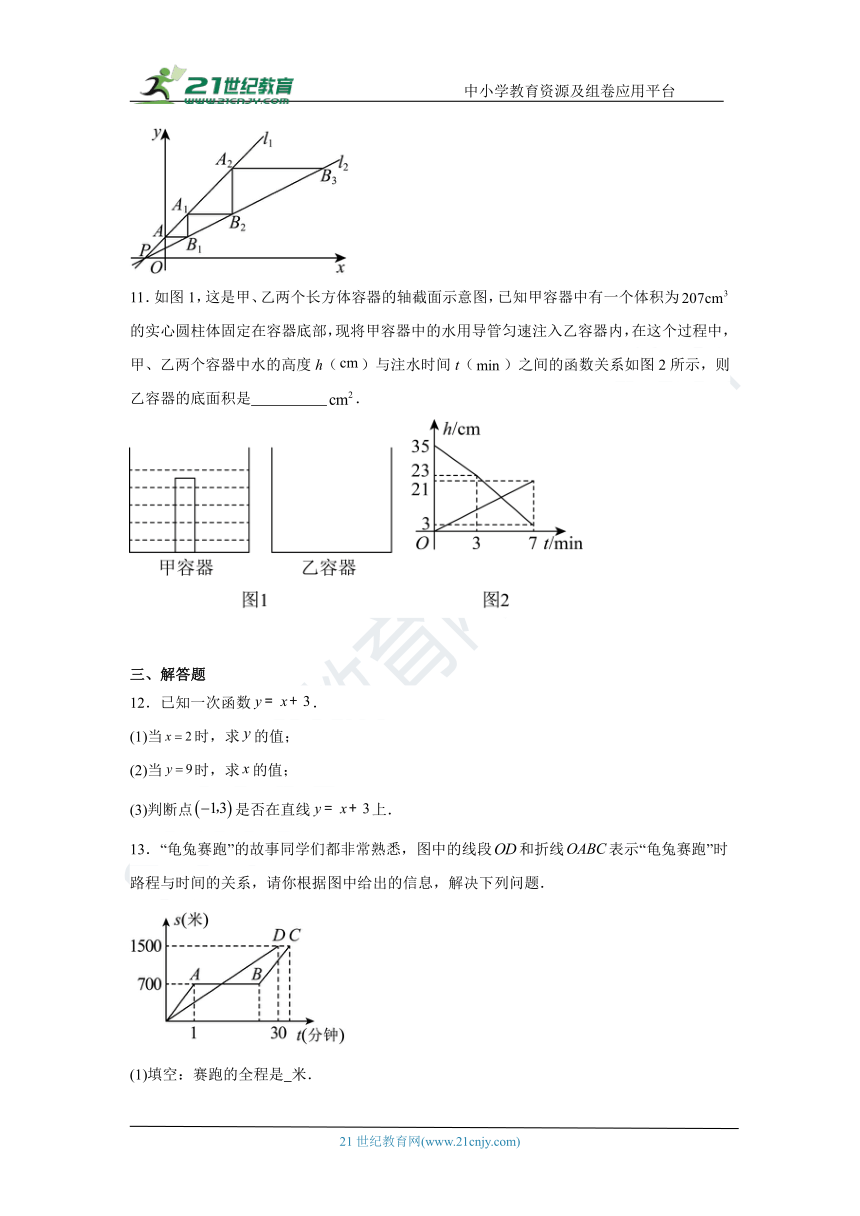
11.如图1,这是甲、乙两个长方体容器的轴截面示意图,已知甲容器中有一个体积为的实心圆柱体固定在容器底部,现将甲容器中的水用导管匀速注入乙容器内,在这个过程中,甲、乙两个容器中水的高度h()与注水时间t()之间的函数关系如图2所示,则乙容器的底面积是 .
三、解答题
12.已知一次函数.
(1)当时,求的值;
(2)当时,求的值;
(3)判断点是否在直线上.
13.“龟兔赛跑”的故事同学们都非常熟悉,图中的线段和折线表示“龟兔赛跑”时路程与时间的关系,请你根据图中给出的信息,解决下列问题.
(1)填空:赛跑的全程是 米.
(2)填空:兔子在起初每分钟跑 米,乌龟每分钟爬 米.
(3)乌龟用了多少分钟追上了正在睡觉的兔子?
(4)兔子醒来,以48千米/时的速度跑向终点,结果还是比乌龟晚到了分钟,请你算算兔子中间停下睡觉用了多少分钟?
14.已知点和直线,则点P到直线的距离可用公式计算.
例如:求点到直线的距离.
解:∵直线,其中,.
∴点到直线的距离为:.
根据以上材料,解答下列问题:
(1)求点到直线:的距离;
(2)直线:沿y轴向上平移2个单位得到直线,求、这两条平行直线之间的距离.
参考答案:
1.D
【分析】根据距离的非负性判断即可.
【详解】根据题意,y关于x的函数解析式为,
故选D.
【点睛】本题考查了数轴上两点间的距离,距离的非负性,熟练掌握距离的非负性是解题的关键.
2.B
【分析】把点代入函数中,可直接求k的值.
【详解】解:把点代入函数中,
得,
解得
故选:B.
【点睛】本题主要考查一次函数图象上点的坐标特征,明确函数图象上点的坐标能使表达式成立是解答本题的关键.
3.B
【分析】先将一次函数解析式变形为,即可确定定点坐标.
【详解】解:∵,
当时,,
∴无论k取何值,该函数的图像总经过一个定点;
故选:B.
【点睛】本题考查了一次函数图像上点的坐标特征,将一次函数变形为是解题的关键.
4.B
【分析】直接根据正比例函数的图象与性质特点逐项判断即可得.
【详解】解:A、当时,,
则函数图象不经过点,此项错误,不符合题意;
B、函数中的,
则函数图象经过第一、三象限,此项正确,符合题意;
C、函数中的,
则随的增大而增大,此项错误,不符合题意;
D、只有当时,,则此项错误,不符合题意;
故选:B.
【点睛】本题考查了正比例函数的图象与性质,熟练掌握正比例函数的图象与性质是解题关键.
5.C
【分析】根据题意可分两段进行分析:当水的深度未超过球顶时;当水的深度超过球顶时,分别分析出水槽中装水部分的宽度变化情况,进而判断出水的深度变化快慢,以此得出答案.
【详解】解:根据题意得:
当水的深度未超过球顶时,水槽中能装水的部分的宽度由下到上,由宽逐渐变窄,再变宽,所以在匀速注水过程中,水的深度变化从上升较慢变为较快,再变为较慢,
当水的深度超过球顶时,水槽中能装水的部分宽度不再变化,所以在匀速注水过程中,水的深度的上升速度不会发生变化,
综上所述,水的深度先上升较慢,再变快,然后变慢,最后匀速上升,
故选:C.
【点睛】本题主要考查函数的图像,利用分类讨论思想,根据不同时间段能装水部分的宽度的变化情况分析水的深度变化情况是解题的关键.
6.D
【分析】根据题意可以求得点的坐标,点的坐标,点的坐标,然后即可发现坐标变化的规律,从而可以求得点的坐标.
【详解】解:由题意可得,点的坐标为,
设点的坐标为,
∵,
解得,,(负根舍去)
∴点的坐标为,
同理可得,点的坐标为,点的坐标为,
点的坐标为,点的坐标为,
……
∴点的坐标为,
故选:D.
【点睛】本题考查一次函数图象上点的坐标特征、点的坐标,解答本题的关键是明确题意,发现题目中坐标的变化规律,求出相应的点的坐标.
7.B
【分析】根据图象先求出两条直线的解析式,然后时代入各自的解析式就可以求出各自的付费情况从而求出结论.
【详解】解:设种方式直线的解析式为:,种方式直线的解析式为:,
由图象可得:,,
解得,,
这两个函数的解析式分别为:,,
当时,
,,
两种方式的电话费相差:,
故选B.
【点睛】本题考查一次函数的实际应用,解题的关键是读懂题意,求出函数解析式.
8.30
【分析】由第一段路程求出小明的骑车速度,从而得到爸爸的速度.对滨江公园离家距离设未知数,根据小明走的路程和爸爸走的路程相等列出方程,最后解方程求出答案.
【详解】解:由第一段路程速度时间
得小明的速度为
爸爸驾车的速度是小明骑车速度的3倍
爸爸的速度为
设爸爸到达时间为
故小明到达时间为
根据小明走的路程和爸爸走的路程相等
列出方程
化简得
合并同类项
解得
滨江公园离家的距离
故滨江公园离家的距离.
故答案为:30
【点睛】本题考查一次函数的应用,解题关键是根据实际问题并结合函数的图像得出解题需要的信息.本题需要较强的图形处理能力.
9.③
【分析】由时,一次函数值y随x的增大而增大;可判断① ;由时,则,可判断②;当时,则,可判断③;由一次函数图象的平移规则:上加下减,可判断④ ;从而可得答案.
【详解】解:①当时,y随x的增大而增大;故① 不符合题意;
②当时,则,函数图象经过一、三、四象限;故② 不符合题意;
③当时,则,∴函数图象一定经过点;故③ 符合题意;
④将直线向下移动2个单位长度后所得直线表达式为,故④ 不符合题意;
故答案为:③
【点睛】本题考查了一次函数的图象与性质,一次函数图象的平移,根据一次函数的解析式判断其图象经过的象限,熟练掌握该知识点是解答关键.
10.
【分析】当,,解得,;当,,解得,;当,,解得,;当,,解得,;同理可得;;;;可推导一般性规律为,然后求解作答即可.
【详解】解:当,,解得,;
当,,解得,;
当,,解得,;
当,,解得,;
同理可得;;;;
∴可推导一般性规律为,
∴,
故答案为:.
【点睛】本题考查了一次函数图象点坐标规律探究.解题的关键在于根据题意推导出一般性规律.
11.60
【分析】设甲容器底面积为,乙容器底面积为,根据拐点可得实心铁柱的高为,可得实心铁柱的底面积,根据函数图象可求得甲容器的高度与时间的函数解析式和乙容器的高度与时间的函数解析式,再结合函数图象,甲容器减少的水的体积刚好等于乙容器增加的水的体积,列出方程求解即可.
【详解】解:设甲容器底面积为,乙容器底面积为,
根据图象可知,拐点
∴实心铁柱的高为,
∴实心铁柱的底面积为,
甲容器的高度与时间的函数图象分为2段,
,函数图象过点,
可得函数解析式为,
,函数图象过点,
可得函数解析式为,
乙容器的高度与时间的图象经过点,,
∴,
当时,,
,,
∴,
,
∵,
∴,
故答案为:60.
【点睛】本题考查一次函数的实际应用,利用数形结合的思想是解题的关键.
12.(1)的值为5
(2)的值为6
(3)点不在直线上
【分析】(1)把代入解析式求得即可;
(2)把代入解析式求得即可;
(3)把代入求得的值,进行比较即可得到答案.
【详解】(1)解:当时,,
的值为5;
(2)解:当时,,
解得:,
的值为6;
(3)解:当时,,
点不在直线上.
【点睛】本题考查了一次函数图象上点的坐标特征,熟练掌握一次函数图象上点的坐标特征是解题的关键.
13.(1)1500
(2)700,50
(3)14分钟
(4)分钟
【分析】(1)利用乌龟始终运动,中间没有停留,进而得出线段的意义和全程的距离;
(2)根据图象中点A、D实际意义可得速度;
(3)根据乌龟所走路程除以所用时间即可解答;
(4)根据速度等于路程除以速度,求得兔子睡醒后跑向终点所用的时间,进而根据题意,即可求解.
【详解】(1)(1)龟始终运动,中间没有停留,
折线表示赛跑过程中兔子的路程与时间的关系,
由图可知,赛跑的全程是1500米;
故答案为:1500;
(2)结合图象得出:兔子在起初每分钟跑700米,
乌龟每分钟爬(米),
答:兔子在起初每分钟跑700米;乌龟每分钟爬50米;
故答案为:700,50;
(3)∵乌龟的速度是:(米/分钟),
∴(分钟),
答:乌龟用了14分钟追上正在睡觉的兔子;
(4)∵48千米/时=米/分钟
∴兔子睡醒后跑向终点所用的时间:(分钟)
∴(分钟),
∴兔子中间停下睡觉用了分钟.
【点睛】此题考查函数图象的实际应用,了解故事内容,正确理解图象的含义,明确各点代表的意义,掌握路程、时间、速度之间的关系是解题的关键.
14.(1)
(2)
【分析】(1)根据点到直线的距离公式直接计算即可;
(2)先根据平移求出直线的解析式,在直线上任意取一点,然后计算这个点到直线的距离即可.
【详解】(1)解:∵直线,其中,.
∴点到直线的距离为:.
(2)解:∵直线:沿y轴向上平移2个单位得到直线,
∴直线的解析式为,
当时,,即点在直线上,
∵直线:,其中,,
∴点到直线的距离为:.
∴、这两条平行直线之间的距离为.
【点睛】本题考查一次函数图象的平移,平行线之间的距离等,解题的关键是能够理解题目中距离的计算公式求得点到直线的距离.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
第四章 一次函数 单元练习 2023-2024学年北师大版八年级数学上册(含解析)
一、单选题
1.若点是x轴上的一个动点,它与x轴上表示3的点的距离是y,则y关于x的函数解析式为( )
A. B. C. D.
2.若函数的图象经过点,则的值是( )
A.4 B. C.2 D.
3.已知一次函数(k为常数,且),无论k取何值,该函数的图像总经过一个定点,则这个定点的坐标是( )
A. B. C. D.
4.下列关于函数的结论正确的是( )
A.函数图象经过点
B.函数图象经过第一、三象限
C.y随x的增大而减小
D.不论x为何值,总有
5.如图所示,一个实心铁球静止在长方体水槽的底部,现向水槽匀速注水,下列图像中能大致反映水槽中水的深度与注水时间关系的是( )
A. B.
C. D.
6.如图,平面直角坐标系中,点的坐标为,以O为圆心,的长为半径画弧,交直线于点;过点作轴交直线于点,以O为圆心,长为半径画弧,交直线于点;过点作轴交直线于点,以点O为圆心,长为半径画弧,交直线于点;…按如此规律进行下去,点的坐标为( )
A. B. C. D.
7.某电信公司推出两种不同的收费标准:A种方式是月租20元;B种方式是月租0元.一个月本地网内打出电话费S(元)与打出时间t(分)的函数图象如图所示,当打出150分钟时,这两种方式的电话费相差( )
A.5元 B.10元 C.15元 D.20元
二、填空题
8.周末,小明和哥哥一起骑自行车从家里出发到滨江公园游玩,从家出发0.5小时后到武山湖,游玩一段时间后按原速前往滨江公园,小明离家80分钟后,爸爸驾车沿相同路线前往滨江公园,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象,已知爸爸驾车的速度是小明骑车速度的3倍,如果小明比爸爸晚10分钟到达滨江公园,那么滨江公园离家的距离是 km.
9.关于一次函数有如下说法:
①当时,y随x的增大而减小;
②当时,函数图象经过二、三、四象限;
③函数图象一定经过点;
④将直线向下移动2个单位长度后所得直线表达式为.
其中说法正确的序号是 .
10.如图,直线:与直线:在轴上相交于点.直线与轴交于点.一动点从点出发,先沿平行于轴的方向运动,到达直线上的点处后,改为垂直于轴的方向运动,到达直线上的点处后,再沿平行于轴的方向运动,到达直线上的点处后,又改为垂直于轴的方向运动,到达直线上的点处后,仍沿平行于轴的方向运动,一照此规律运动,动点依次经过点,,,,,,…则当动点到达处时,点的坐标为 .
11.如图1,这是甲、乙两个长方体容器的轴截面示意图,已知甲容器中有一个体积为的实心圆柱体固定在容器底部,现将甲容器中的水用导管匀速注入乙容器内,在这个过程中,甲、乙两个容器中水的高度h()与注水时间t()之间的函数关系如图2所示,则乙容器的底面积是 .
三、解答题
12.已知一次函数.
(1)当时,求的值;
(2)当时,求的值;
(3)判断点是否在直线上.
13.“龟兔赛跑”的故事同学们都非常熟悉,图中的线段和折线表示“龟兔赛跑”时路程与时间的关系,请你根据图中给出的信息,解决下列问题.
(1)填空:赛跑的全程是 米.
(2)填空:兔子在起初每分钟跑 米,乌龟每分钟爬 米.
(3)乌龟用了多少分钟追上了正在睡觉的兔子?
(4)兔子醒来,以48千米/时的速度跑向终点,结果还是比乌龟晚到了分钟,请你算算兔子中间停下睡觉用了多少分钟?
14.已知点和直线,则点P到直线的距离可用公式计算.
例如:求点到直线的距离.
解:∵直线,其中,.
∴点到直线的距离为:.
根据以上材料,解答下列问题:
(1)求点到直线:的距离;
(2)直线:沿y轴向上平移2个单位得到直线,求、这两条平行直线之间的距离.
参考答案:
1.D
【分析】根据距离的非负性判断即可.
【详解】根据题意,y关于x的函数解析式为,
故选D.
【点睛】本题考查了数轴上两点间的距离,距离的非负性,熟练掌握距离的非负性是解题的关键.
2.B
【分析】把点代入函数中,可直接求k的值.
【详解】解:把点代入函数中,
得,
解得
故选:B.
【点睛】本题主要考查一次函数图象上点的坐标特征,明确函数图象上点的坐标能使表达式成立是解答本题的关键.
3.B
【分析】先将一次函数解析式变形为,即可确定定点坐标.
【详解】解:∵,
当时,,
∴无论k取何值,该函数的图像总经过一个定点;
故选:B.
【点睛】本题考查了一次函数图像上点的坐标特征,将一次函数变形为是解题的关键.
4.B
【分析】直接根据正比例函数的图象与性质特点逐项判断即可得.
【详解】解:A、当时,,
则函数图象不经过点,此项错误,不符合题意;
B、函数中的,
则函数图象经过第一、三象限,此项正确,符合题意;
C、函数中的,
则随的增大而增大,此项错误,不符合题意;
D、只有当时,,则此项错误,不符合题意;
故选:B.
【点睛】本题考查了正比例函数的图象与性质,熟练掌握正比例函数的图象与性质是解题关键.
5.C
【分析】根据题意可分两段进行分析:当水的深度未超过球顶时;当水的深度超过球顶时,分别分析出水槽中装水部分的宽度变化情况,进而判断出水的深度变化快慢,以此得出答案.
【详解】解:根据题意得:
当水的深度未超过球顶时,水槽中能装水的部分的宽度由下到上,由宽逐渐变窄,再变宽,所以在匀速注水过程中,水的深度变化从上升较慢变为较快,再变为较慢,
当水的深度超过球顶时,水槽中能装水的部分宽度不再变化,所以在匀速注水过程中,水的深度的上升速度不会发生变化,
综上所述,水的深度先上升较慢,再变快,然后变慢,最后匀速上升,
故选:C.
【点睛】本题主要考查函数的图像,利用分类讨论思想,根据不同时间段能装水部分的宽度的变化情况分析水的深度变化情况是解题的关键.
6.D
【分析】根据题意可以求得点的坐标,点的坐标,点的坐标,然后即可发现坐标变化的规律,从而可以求得点的坐标.
【详解】解:由题意可得,点的坐标为,
设点的坐标为,
∵,
解得,,(负根舍去)
∴点的坐标为,
同理可得,点的坐标为,点的坐标为,
点的坐标为,点的坐标为,
……
∴点的坐标为,
故选:D.
【点睛】本题考查一次函数图象上点的坐标特征、点的坐标,解答本题的关键是明确题意,发现题目中坐标的变化规律,求出相应的点的坐标.
7.B
【分析】根据图象先求出两条直线的解析式,然后时代入各自的解析式就可以求出各自的付费情况从而求出结论.
【详解】解:设种方式直线的解析式为:,种方式直线的解析式为:,
由图象可得:,,
解得,,
这两个函数的解析式分别为:,,
当时,
,,
两种方式的电话费相差:,
故选B.
【点睛】本题考查一次函数的实际应用,解题的关键是读懂题意,求出函数解析式.
8.30
【分析】由第一段路程求出小明的骑车速度,从而得到爸爸的速度.对滨江公园离家距离设未知数,根据小明走的路程和爸爸走的路程相等列出方程,最后解方程求出答案.
【详解】解:由第一段路程速度时间
得小明的速度为
爸爸驾车的速度是小明骑车速度的3倍
爸爸的速度为
设爸爸到达时间为
故小明到达时间为
根据小明走的路程和爸爸走的路程相等
列出方程
化简得
合并同类项
解得
滨江公园离家的距离
故滨江公园离家的距离.
故答案为:30
【点睛】本题考查一次函数的应用,解题关键是根据实际问题并结合函数的图像得出解题需要的信息.本题需要较强的图形处理能力.
9.③
【分析】由时,一次函数值y随x的增大而增大;可判断① ;由时,则,可判断②;当时,则,可判断③;由一次函数图象的平移规则:上加下减,可判断④ ;从而可得答案.
【详解】解:①当时,y随x的增大而增大;故① 不符合题意;
②当时,则,函数图象经过一、三、四象限;故② 不符合题意;
③当时,则,∴函数图象一定经过点;故③ 符合题意;
④将直线向下移动2个单位长度后所得直线表达式为,故④ 不符合题意;
故答案为:③
【点睛】本题考查了一次函数的图象与性质,一次函数图象的平移,根据一次函数的解析式判断其图象经过的象限,熟练掌握该知识点是解答关键.
10.
【分析】当,,解得,;当,,解得,;当,,解得,;当,,解得,;同理可得;;;;可推导一般性规律为,然后求解作答即可.
【详解】解:当,,解得,;
当,,解得,;
当,,解得,;
当,,解得,;
同理可得;;;;
∴可推导一般性规律为,
∴,
故答案为:.
【点睛】本题考查了一次函数图象点坐标规律探究.解题的关键在于根据题意推导出一般性规律.
11.60
【分析】设甲容器底面积为,乙容器底面积为,根据拐点可得实心铁柱的高为,可得实心铁柱的底面积,根据函数图象可求得甲容器的高度与时间的函数解析式和乙容器的高度与时间的函数解析式,再结合函数图象,甲容器减少的水的体积刚好等于乙容器增加的水的体积,列出方程求解即可.
【详解】解:设甲容器底面积为,乙容器底面积为,
根据图象可知,拐点
∴实心铁柱的高为,
∴实心铁柱的底面积为,
甲容器的高度与时间的函数图象分为2段,
,函数图象过点,
可得函数解析式为,
,函数图象过点,
可得函数解析式为,
乙容器的高度与时间的图象经过点,,
∴,
当时,,
,,
∴,
,
∵,
∴,
故答案为:60.
【点睛】本题考查一次函数的实际应用,利用数形结合的思想是解题的关键.
12.(1)的值为5
(2)的值为6
(3)点不在直线上
【分析】(1)把代入解析式求得即可;
(2)把代入解析式求得即可;
(3)把代入求得的值,进行比较即可得到答案.
【详解】(1)解:当时,,
的值为5;
(2)解:当时,,
解得:,
的值为6;
(3)解:当时,,
点不在直线上.
【点睛】本题考查了一次函数图象上点的坐标特征,熟练掌握一次函数图象上点的坐标特征是解题的关键.
13.(1)1500
(2)700,50
(3)14分钟
(4)分钟
【分析】(1)利用乌龟始终运动,中间没有停留,进而得出线段的意义和全程的距离;
(2)根据图象中点A、D实际意义可得速度;
(3)根据乌龟所走路程除以所用时间即可解答;
(4)根据速度等于路程除以速度,求得兔子睡醒后跑向终点所用的时间,进而根据题意,即可求解.
【详解】(1)(1)龟始终运动,中间没有停留,
折线表示赛跑过程中兔子的路程与时间的关系,
由图可知,赛跑的全程是1500米;
故答案为:1500;
(2)结合图象得出:兔子在起初每分钟跑700米,
乌龟每分钟爬(米),
答:兔子在起初每分钟跑700米;乌龟每分钟爬50米;
故答案为:700,50;
(3)∵乌龟的速度是:(米/分钟),
∴(分钟),
答:乌龟用了14分钟追上正在睡觉的兔子;
(4)∵48千米/时=米/分钟
∴兔子睡醒后跑向终点所用的时间:(分钟)
∴(分钟),
∴兔子中间停下睡觉用了分钟.
【点睛】此题考查函数图象的实际应用,了解故事内容,正确理解图象的含义,明确各点代表的意义,掌握路程、时间、速度之间的关系是解题的关键.
14.(1)
(2)
【分析】(1)根据点到直线的距离公式直接计算即可;
(2)先根据平移求出直线的解析式,在直线上任意取一点,然后计算这个点到直线的距离即可.
【详解】(1)解:∵直线,其中,.
∴点到直线的距离为:.
(2)解:∵直线:沿y轴向上平移2个单位得到直线,
∴直线的解析式为,
当时,,即点在直线上,
∵直线:,其中,,
∴点到直线的距离为:.
∴、这两条平行直线之间的距离为.
【点睛】本题考查一次函数图象的平移,平行线之间的距离等,解题的关键是能够理解题目中距离的计算公式求得点到直线的距离.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
