3.1函数的概念及其表示 同步练习(含答案)
文档属性
| 名称 | 3.1函数的概念及其表示 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 182.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-14 17:26:20 | ||
图片预览



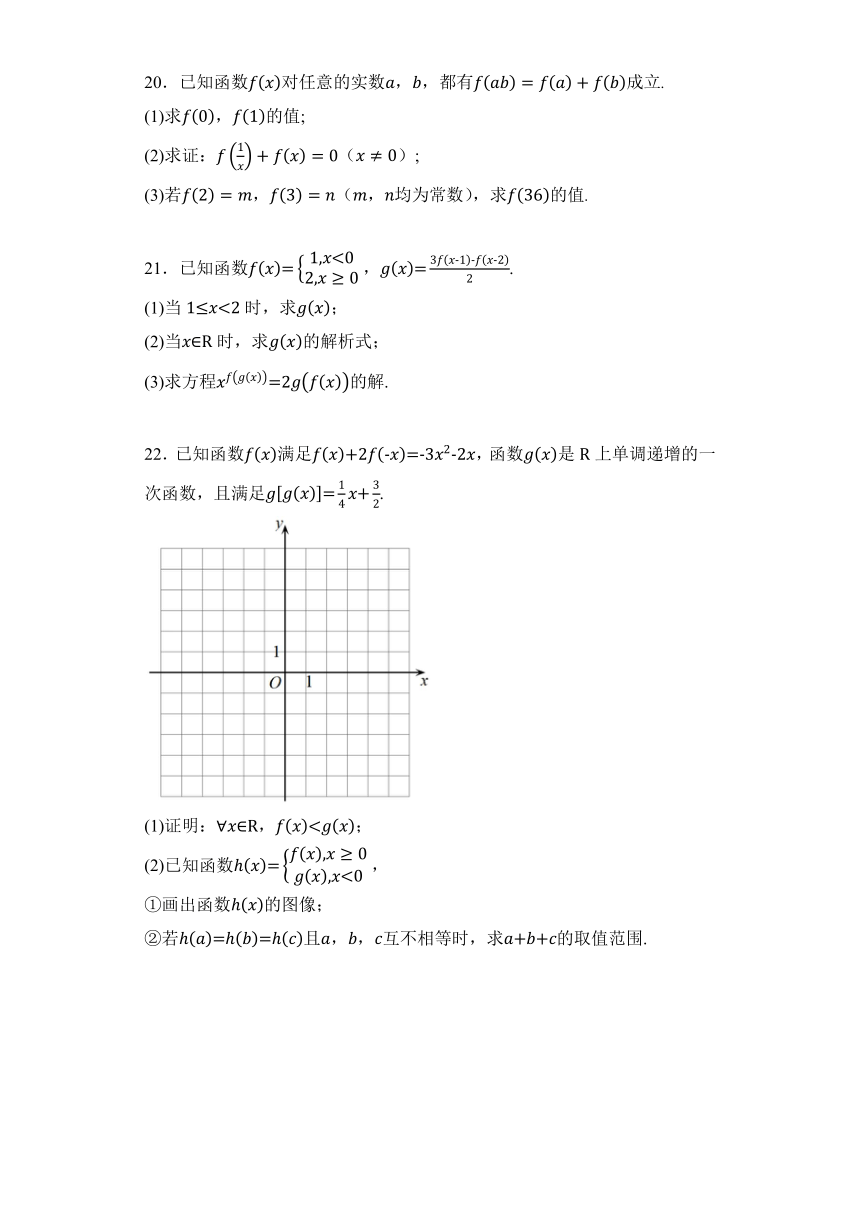
文档简介
3.1 函数的概念及其表示
一、单选题
1.函数,则( ).
A. B. C. D.
2.某天0时,小鹏同学生病了,体温上升,吃过药后感觉好多了,中午时他的体温基本正常(正常体温为37 ℃),但是下午他的体温又开始上升,直到半夜才感觉身上不那么发烫了.下面能大致反映出小鹏这一天(0时至24时)体温变化情况的图像是( )
A. B.
C. D.
3.已知函数的定义域为,则其值域为( )
A. B. C. D.
4.下列说法不正确的是( )
A.圆的周长与其直径的比值是常量
B.任意凸四边形的内角和的度数是常量
C.发射升空的火箭高度与发射的时间之间是函数关系
D.某商品的广告费用与销售量之间是函数关系
5.下列各变量间不存在依赖关系的是( )
A.扇形的圆心角与它的面积
B.某人的体重与其饮食情况
C.水稻的亩产量与施肥量
D.某人的衣着价格与视力
6.某家庭利用十一长假外出自驾游,为保证行车顺利,每次加油都把油箱加满,如表记录了该家庭用车相邻两次加油时的情况.
加油时间 加油量/升 加油时的累计里程/千米
2020年10月1日 12 32000
2020年10月6日 48 32600
(注:“累计里程”指汽车从出厂开始累计行驶的路程.)在这段时间内,该车每100千米平均耗油量为( )
A.6升 B.8升 C.10升 D.12升
7.函数的值域是( )
A. B.
C. D.
8.若,则函数的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
二、多选题
9.下列说法中,正确的有( )
A.函数就是两个集合之间的对应关系
B.若函数的值域只含有一个元素,则定义域也只含有一个元素
C.若,则一定成立
D.若定义域和对应关系确定,值域也就确定了
10.对于函数,若,则下列说法正确的是( )
A. B.若,则
C.若,则 D.有且只有一个
11.设,则用表示不超过的最大整数,例如,.已知函数,则函数的值域中含有的元素可能是( )
A. B. C. D.
12.具有性质的函数,我们称为满足“倒负”变换的函数.下列函数:①;②;③中满足“倒负”变换的函数是( )
A.① B.② C.③ D.都不是
三、填空题
13.复合函数:形如形式的函数称为复合函数,其中称为 ,称为内函数
14.若的值域为,则的值域为 .
15.已知,则 .
16.如图所示,变量y与时间t(s)的图象如图所示,则时间t至少隔 s时,y=1会重复出现1次.
四、解答题
17.有研究表明,声速与气温有关,当气温变化时,声速也将随着变化.声速与气温关系的一些数据如下表所示.
气温/℃ … -20 -10 0 10 20 30 …
声速/(m/s) … 318 324 330 336 342 348 …
(1)指出在这个变化过程中的自变量和因变量.
(2)当声速为342m/s时,气温为多少?
(3)根据表中数据判断,气温每升高10℃时,声速将增大(或减少)多少?
18.已知集合,是定义在上的函数,已知把中的每一个自然数对应到它的各个数字之和.
(1)求的值;
(2)若,求的值;
(3)计算:.
19.已知的定义域为,求的定义域.
20.已知函数对任意的实数,,都有成立.
(1)求,的值;
(2)求证:();
(3)若,(,均为常数),求的值.
21.已知函数,.
(1)当时,求;
(2)当时,求的解析式;
(3)求方程的解.
22.已知函数满足,函数是上单调递增的一次函数,且满足.
(1)证明:,;
(2)已知函数,
①画出函数的图像;
②若且,,互不相等时,求的取值范围.
参考答案:
1.A2.C3.A4.D5.D6.B7.D8.B
9.CD
10.ABD
11.BC
12.AC
13.外函数
14.
15.1
16.2
17.(1)由题意,得气温变化时,声速也将随着变化,因此自变量是气温,因变量是声速.
(2)根据题设中给出的数据表,知当声速为342m/s时,气温为20℃.
(3)因为324-318=330-324=336-330=342-336=348-342=6,
所以气温每升高10℃时,声速将增大6m/s.
18.(1)由题意得:
(2)由,设,
由题意,
所以或或或
或或或或,
所以或或或
或或或或.
(3)由题意:
,
,
,
,
,
,
,
,
所以:
.
19.的定义域为
,
即的定义域为;
,即
所以的定义域
20.(1)令,则,故.
令,则,故.
(2),,又,
故().
(3),
,
故.
21.(1)当时,,所以;,所以;
所以;
(2)当时,,所以;,所以;
所以;
当时,由(1)知,;
当时,,所以;,所以;
所以.
综上所述:
(3)因为,所以.
当时,;
当时,;
所以,关于x的方程即为
解得:或.
22.(1)证明:由,得:;
联立,消去得:;
又由函数是上单调递增的一次函数,设(),
则,
即,且,解得:;
所以,
对于,有,
对,,则;
综上:,.
(2)由(1)得,;
①作出的函数图像,如图所示:
②不妨设,由①函数的图像可得:,
即,,,且等号同时成立,又,即.
故的取值范围为.
一、单选题
1.函数,则( ).
A. B. C. D.
2.某天0时,小鹏同学生病了,体温上升,吃过药后感觉好多了,中午时他的体温基本正常(正常体温为37 ℃),但是下午他的体温又开始上升,直到半夜才感觉身上不那么发烫了.下面能大致反映出小鹏这一天(0时至24时)体温变化情况的图像是( )
A. B.
C. D.
3.已知函数的定义域为,则其值域为( )
A. B. C. D.
4.下列说法不正确的是( )
A.圆的周长与其直径的比值是常量
B.任意凸四边形的内角和的度数是常量
C.发射升空的火箭高度与发射的时间之间是函数关系
D.某商品的广告费用与销售量之间是函数关系
5.下列各变量间不存在依赖关系的是( )
A.扇形的圆心角与它的面积
B.某人的体重与其饮食情况
C.水稻的亩产量与施肥量
D.某人的衣着价格与视力
6.某家庭利用十一长假外出自驾游,为保证行车顺利,每次加油都把油箱加满,如表记录了该家庭用车相邻两次加油时的情况.
加油时间 加油量/升 加油时的累计里程/千米
2020年10月1日 12 32000
2020年10月6日 48 32600
(注:“累计里程”指汽车从出厂开始累计行驶的路程.)在这段时间内,该车每100千米平均耗油量为( )
A.6升 B.8升 C.10升 D.12升
7.函数的值域是( )
A. B.
C. D.
8.若,则函数的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
二、多选题
9.下列说法中,正确的有( )
A.函数就是两个集合之间的对应关系
B.若函数的值域只含有一个元素,则定义域也只含有一个元素
C.若,则一定成立
D.若定义域和对应关系确定,值域也就确定了
10.对于函数,若,则下列说法正确的是( )
A. B.若,则
C.若,则 D.有且只有一个
11.设,则用表示不超过的最大整数,例如,.已知函数,则函数的值域中含有的元素可能是( )
A. B. C. D.
12.具有性质的函数,我们称为满足“倒负”变换的函数.下列函数:①;②;③中满足“倒负”变换的函数是( )
A.① B.② C.③ D.都不是
三、填空题
13.复合函数:形如形式的函数称为复合函数,其中称为 ,称为内函数
14.若的值域为,则的值域为 .
15.已知,则 .
16.如图所示,变量y与时间t(s)的图象如图所示,则时间t至少隔 s时,y=1会重复出现1次.
四、解答题
17.有研究表明,声速与气温有关,当气温变化时,声速也将随着变化.声速与气温关系的一些数据如下表所示.
气温/℃ … -20 -10 0 10 20 30 …
声速/(m/s) … 318 324 330 336 342 348 …
(1)指出在这个变化过程中的自变量和因变量.
(2)当声速为342m/s时,气温为多少?
(3)根据表中数据判断,气温每升高10℃时,声速将增大(或减少)多少?
18.已知集合,是定义在上的函数,已知把中的每一个自然数对应到它的各个数字之和.
(1)求的值;
(2)若,求的值;
(3)计算:.
19.已知的定义域为,求的定义域.
20.已知函数对任意的实数,,都有成立.
(1)求,的值;
(2)求证:();
(3)若,(,均为常数),求的值.
21.已知函数,.
(1)当时,求;
(2)当时,求的解析式;
(3)求方程的解.
22.已知函数满足,函数是上单调递增的一次函数,且满足.
(1)证明:,;
(2)已知函数,
①画出函数的图像;
②若且,,互不相等时,求的取值范围.
参考答案:
1.A2.C3.A4.D5.D6.B7.D8.B
9.CD
10.ABD
11.BC
12.AC
13.外函数
14.
15.1
16.2
17.(1)由题意,得气温变化时,声速也将随着变化,因此自变量是气温,因变量是声速.
(2)根据题设中给出的数据表,知当声速为342m/s时,气温为20℃.
(3)因为324-318=330-324=336-330=342-336=348-342=6,
所以气温每升高10℃时,声速将增大6m/s.
18.(1)由题意得:
(2)由,设,
由题意,
所以或或或
或或或或,
所以或或或
或或或或.
(3)由题意:
,
,
,
,
,
,
,
,
所以:
.
19.的定义域为
,
即的定义域为;
,即
所以的定义域
20.(1)令,则,故.
令,则,故.
(2),,又,
故().
(3),
,
故.
21.(1)当时,,所以;,所以;
所以;
(2)当时,,所以;,所以;
所以;
当时,由(1)知,;
当时,,所以;,所以;
所以.
综上所述:
(3)因为,所以.
当时,;
当时,;
所以,关于x的方程即为
解得:或.
22.(1)证明:由,得:;
联立,消去得:;
又由函数是上单调递增的一次函数,设(),
则,
即,且,解得:;
所以,
对于,有,
对,,则;
综上:,.
(2)由(1)得,;
①作出的函数图像,如图所示:
②不妨设,由①函数的图像可得:,
即,,,且等号同时成立,又,即.
故的取值范围为.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
