1.3正方形的性质与判定同步练习 2023--2024学年北师大版数学九年级上册(含答案)
文档属性
| 名称 | 1.3正方形的性质与判定同步练习 2023--2024学年北师大版数学九年级上册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 530.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-16 02:29:36 | ||
图片预览


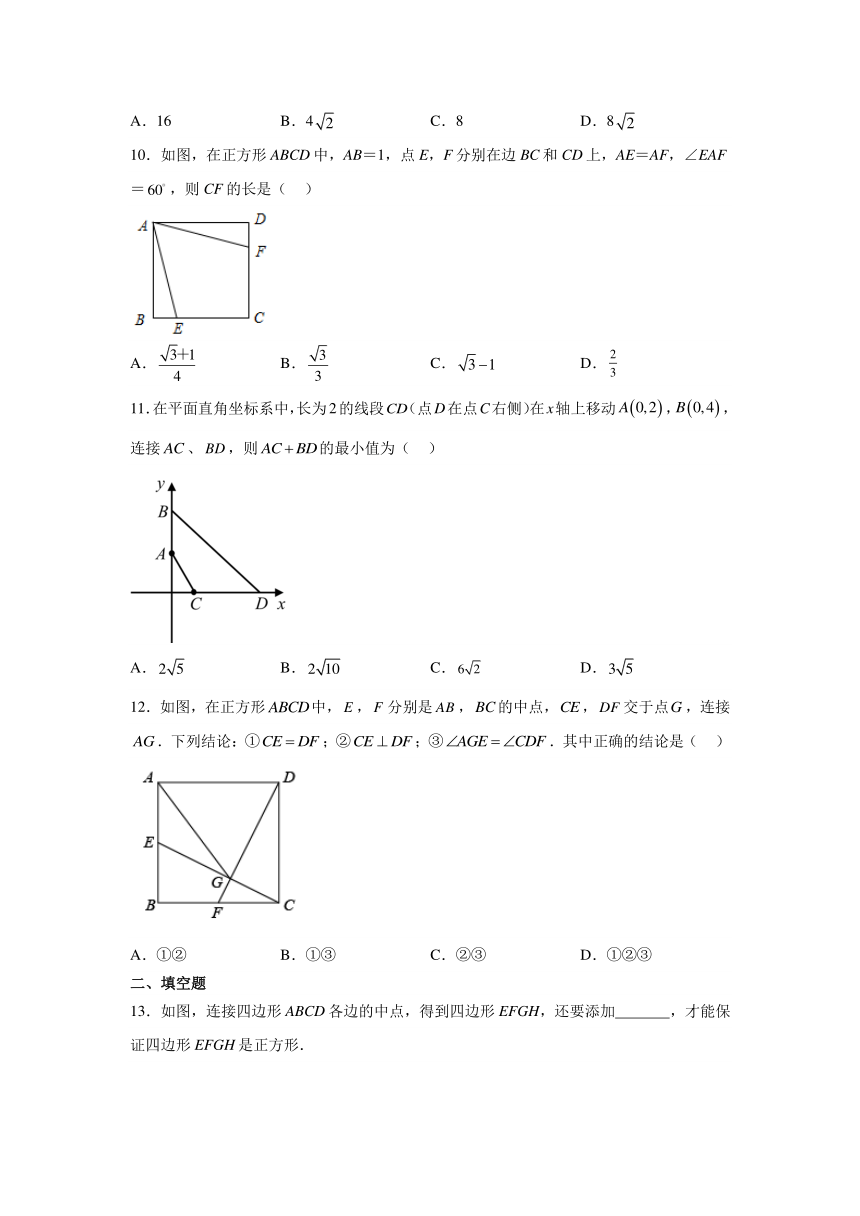
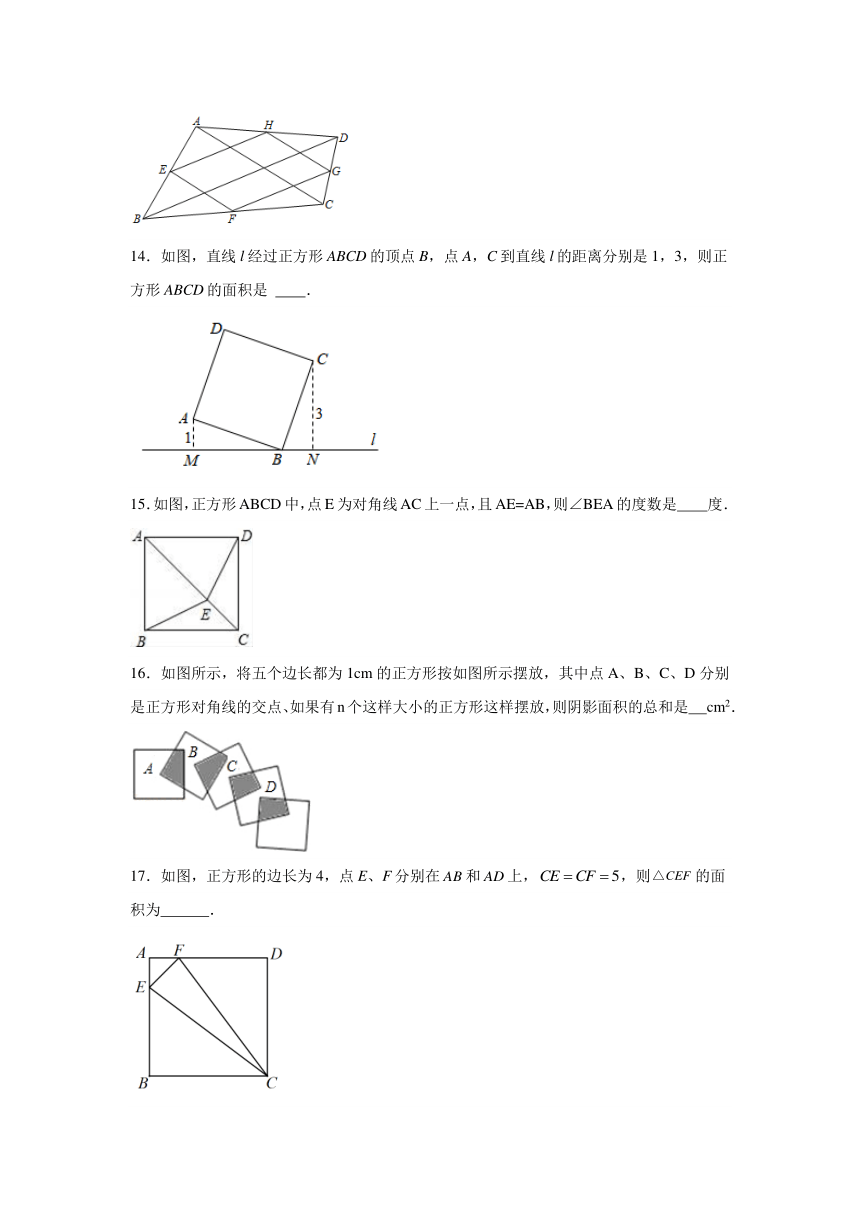

文档简介
1.3正方形的性质与判定同步练习
一、单选题
1.如图,在边长为1的正方形中,当第1次作,第2次作;第3次作,……依次方法继续作垂直线段,当作到第10次时,所得的最小的三角形的面积是( )
A. B. C. D.
2.如图,将长方形纸片折叠,使A点落BC上的F处,折痕为BE,若沿EF剪下,则折叠部分是一个正方形,其数学原理是( )
A.邻边相等的矩形是正方形 B.对角线相等的菱形是正方形
C.两个全等的直角三角形构成正方形 D.轴对称图形是正方形
3.如图,将正方形OABC放在平面直角坐标系中,O是原点,点A的坐标为(1,),则点C的坐标为( )
A.(﹣1,﹣) B.(,﹣1) C.(﹣1,) D.(﹣,1)
4.如图,在正方形ABCD中,E、F是对角线BD上的点,AB=BF=DE,则∠EAF的度数为( )
A.22.5° B.30° C.45° D.67.5°
5.四边形ABCD是边长为16的菱形,顺次连接它的各边中点组成四边形EFGH(四边形EFGH称为原四边形ABCD的中点四边形),再顺次连接四边形EFGH的各边中点组成第二个中点四边形,…,则按上述规律组成的第八个中点四边形的周长等于( )
A. B.1 C.4 D.8
6.正方形具有而矩形不一定有的性质是( )
A.对角线互相垂直 B.对角线相等
C.对角互补 D.四个角相等
7.如图,在正方形纸片ABCD上,E是AD上一点(不与点A,D重合).将纸片沿BE折叠,使点A落在点A处,延长EA'交CD于点F,则∠EBF=( )
A.40° B.45° C.50° D.不是定值
8.如图,在正方形ABCD中,AB=8,点E,F分别在边AB,CD上,∠EFC=120°,若将四边形EBCF沿EF折叠,点B恰好落在AD边上,则AE的长度为( )
A. B. C. D.
9.正方形的一条对角线之长为4,则此正方形的面积是( )
A.16 B.4 C.8 D.8
10.如图,在正方形ABCD中,AB=1,点E,F分别在边BC和CD上,AE=AF,∠EAF=,则CF的长是( )
A. B. C. D.
11.在平面直角坐标系中,长为2的线段(点D在点C右侧)在x轴上移动,,连接、,则的最小值为( )
A. B. C. D.
12.如图,在正方形中,,分别是,的中点,,交于点,连接.下列结论:①;②;③.其中正确的结论是( )
A.①② B.①③ C.②③ D.①②③
二、填空题
13.如图,连接四边形ABCD各边的中点,得到四边形EFGH,还要添加 ,才能保证四边形EFGH是正方形.
14.如图,直线l经过正方形ABCD的顶点B,点A,C到直线l的距离分别是1,3,则正方形ABCD的面积是 .
15.如图,正方形ABCD中,点E为对角线AC上一点,且AE=AB,则∠BEA的度数是 度.
16.如图所示,将五个边长都为1cm的正方形按如图所示摆放,其中点A、B、C、D分别是正方形对角线的交点、如果有n个这样大小的正方形这样摆放,则阴影面积的总和是 cm2.
17.如图,正方形的边长为4,点E、F分别在和上,,则的面积为 .
三、解答题
18.如图,四边形是正方形,是等边三角形,求的度数.
19.已知矩形ABCD中,E是AD边上的一个动点,点F,G,H分别是BC,BE,CE的中点.
(1)求证:△BGF≌△FHC;
(2)设AD=a,当四边形EGFH是正方形时,求矩形ABCD的面积.
20.如图,在矩形ABCD中,M是边AD的中点,P是边BC上的动点,且,,
垂足分别为E,F.
(1)当矩形ABCD的长与宽满足什么数量关系时,四边形PEMF是矩形?证明你的结论.
(2)若四边形PEMF是矩形,当点P运动到什么位置时,四边形PEMF是正方形?证明你的结论.
21.如图,在平行四边形ABCD中,点E,F分别在边AB,CD上,且四边形BEDF为正方形.
(1)求证;
(2)已知平行四边形ABCD的面积为,.求的长.
22.如图,在正方形ABCD外取一点E,连接AE,BE,DE,过点A作AE的垂线交DE于点P,若,.
(1)求证:;
(2)求证:;
(3)求正方形ABCD的面积.
参考答案
1--10BADCC ABACC 11--12BD
13.AC⊥BD,AC=BD/ AC=BD, AC⊥BD
14.10
15.67.5.
16.
17.
18.解:∵四边形ABCD是正方形,△CBE是等边三角形,
∴AB=BC,∠BAD=90°,BE=BC,∠CBE=60°,
∴AB=BE,∠ABE=90° 60°=30°,
∴∠AEB=∠EAB=(180° 30°)=75°.
19.(1)连接EF,∵点F,G,H分别是BC,BE,CE的中点,
∴FH//BE,FH=BE,FH=BG,
∴∠CFH=∠CBG,
∵BF=CF,
∴△BGF≌△FHC,
(2)当四边形EGFH是正方形时,连接GH,可得:EF⊥GH且EF=GH,
∵在△BEC中,点G,H分别是BE,CE的中点,
∴且GH//BC,
∴EF⊥BC,
∵AD//BC,AB⊥BC,
∴AB=EF=GH=a,
∴矩形ABCD的面积=
20.(1)当时,四边形PEMF是矩形.
证明:∵四边形ABCD是矩形,M是边AD的中点,
∴,.
∵,
∴,
∴,,
∴,
又∵,,
∴,
∴四边形PEMF是矩形,
即当时,四边形PEMF是矩形.
(2)当点P运动到边BC的中点时,矩形PEMF是正方形,此时.
证明:∵四边形PEMF为矩形,
∴.
在和中,,
∴,
∴.
又∵四边形PEMF是矩形,
∴矩形PEMF是正方形,
即当点P运动到BC的中点时,四边形PEMF是正方形.
21.(1)四边形是正方形,是平行四边形,
,,,
在和中,
,
,
;
(2)由题意可知:,
,
,
,,
由(1)得.
22.(1)证明:∵四边形ABCD是正方形,
∴,
∵,
∴.
∴,
即.
∵,
∴.
(2)证明:如下图:
∵,,
∴·
∴,
∵,
∴,
∴,
∴.
(3)解:如图,过点B作交AE的延长线于点F.
∵,,
∴由勾股定理得:.
由(2)知,,
∴由勾股定理得:,
∵,
∴,
∵,
∴,
∴,
由勾股定理得:,
∴,
∴.
∴,
在中,由勾股定理得:,
.
一、单选题
1.如图,在边长为1的正方形中,当第1次作,第2次作;第3次作,……依次方法继续作垂直线段,当作到第10次时,所得的最小的三角形的面积是( )
A. B. C. D.
2.如图,将长方形纸片折叠,使A点落BC上的F处,折痕为BE,若沿EF剪下,则折叠部分是一个正方形,其数学原理是( )
A.邻边相等的矩形是正方形 B.对角线相等的菱形是正方形
C.两个全等的直角三角形构成正方形 D.轴对称图形是正方形
3.如图,将正方形OABC放在平面直角坐标系中,O是原点,点A的坐标为(1,),则点C的坐标为( )
A.(﹣1,﹣) B.(,﹣1) C.(﹣1,) D.(﹣,1)
4.如图,在正方形ABCD中,E、F是对角线BD上的点,AB=BF=DE,则∠EAF的度数为( )
A.22.5° B.30° C.45° D.67.5°
5.四边形ABCD是边长为16的菱形,顺次连接它的各边中点组成四边形EFGH(四边形EFGH称为原四边形ABCD的中点四边形),再顺次连接四边形EFGH的各边中点组成第二个中点四边形,…,则按上述规律组成的第八个中点四边形的周长等于( )
A. B.1 C.4 D.8
6.正方形具有而矩形不一定有的性质是( )
A.对角线互相垂直 B.对角线相等
C.对角互补 D.四个角相等
7.如图,在正方形纸片ABCD上,E是AD上一点(不与点A,D重合).将纸片沿BE折叠,使点A落在点A处,延长EA'交CD于点F,则∠EBF=( )
A.40° B.45° C.50° D.不是定值
8.如图,在正方形ABCD中,AB=8,点E,F分别在边AB,CD上,∠EFC=120°,若将四边形EBCF沿EF折叠,点B恰好落在AD边上,则AE的长度为( )
A. B. C. D.
9.正方形的一条对角线之长为4,则此正方形的面积是( )
A.16 B.4 C.8 D.8
10.如图,在正方形ABCD中,AB=1,点E,F分别在边BC和CD上,AE=AF,∠EAF=,则CF的长是( )
A. B. C. D.
11.在平面直角坐标系中,长为2的线段(点D在点C右侧)在x轴上移动,,连接、,则的最小值为( )
A. B. C. D.
12.如图,在正方形中,,分别是,的中点,,交于点,连接.下列结论:①;②;③.其中正确的结论是( )
A.①② B.①③ C.②③ D.①②③
二、填空题
13.如图,连接四边形ABCD各边的中点,得到四边形EFGH,还要添加 ,才能保证四边形EFGH是正方形.
14.如图,直线l经过正方形ABCD的顶点B,点A,C到直线l的距离分别是1,3,则正方形ABCD的面积是 .
15.如图,正方形ABCD中,点E为对角线AC上一点,且AE=AB,则∠BEA的度数是 度.
16.如图所示,将五个边长都为1cm的正方形按如图所示摆放,其中点A、B、C、D分别是正方形对角线的交点、如果有n个这样大小的正方形这样摆放,则阴影面积的总和是 cm2.
17.如图,正方形的边长为4,点E、F分别在和上,,则的面积为 .
三、解答题
18.如图,四边形是正方形,是等边三角形,求的度数.
19.已知矩形ABCD中,E是AD边上的一个动点,点F,G,H分别是BC,BE,CE的中点.
(1)求证:△BGF≌△FHC;
(2)设AD=a,当四边形EGFH是正方形时,求矩形ABCD的面积.
20.如图,在矩形ABCD中,M是边AD的中点,P是边BC上的动点,且,,
垂足分别为E,F.
(1)当矩形ABCD的长与宽满足什么数量关系时,四边形PEMF是矩形?证明你的结论.
(2)若四边形PEMF是矩形,当点P运动到什么位置时,四边形PEMF是正方形?证明你的结论.
21.如图,在平行四边形ABCD中,点E,F分别在边AB,CD上,且四边形BEDF为正方形.
(1)求证;
(2)已知平行四边形ABCD的面积为,.求的长.
22.如图,在正方形ABCD外取一点E,连接AE,BE,DE,过点A作AE的垂线交DE于点P,若,.
(1)求证:;
(2)求证:;
(3)求正方形ABCD的面积.
参考答案
1--10BADCC ABACC 11--12BD
13.AC⊥BD,AC=BD/ AC=BD, AC⊥BD
14.10
15.67.5.
16.
17.
18.解:∵四边形ABCD是正方形,△CBE是等边三角形,
∴AB=BC,∠BAD=90°,BE=BC,∠CBE=60°,
∴AB=BE,∠ABE=90° 60°=30°,
∴∠AEB=∠EAB=(180° 30°)=75°.
19.(1)连接EF,∵点F,G,H分别是BC,BE,CE的中点,
∴FH//BE,FH=BE,FH=BG,
∴∠CFH=∠CBG,
∵BF=CF,
∴△BGF≌△FHC,
(2)当四边形EGFH是正方形时,连接GH,可得:EF⊥GH且EF=GH,
∵在△BEC中,点G,H分别是BE,CE的中点,
∴且GH//BC,
∴EF⊥BC,
∵AD//BC,AB⊥BC,
∴AB=EF=GH=a,
∴矩形ABCD的面积=
20.(1)当时,四边形PEMF是矩形.
证明:∵四边形ABCD是矩形,M是边AD的中点,
∴,.
∵,
∴,
∴,,
∴,
又∵,,
∴,
∴四边形PEMF是矩形,
即当时,四边形PEMF是矩形.
(2)当点P运动到边BC的中点时,矩形PEMF是正方形,此时.
证明:∵四边形PEMF为矩形,
∴.
在和中,,
∴,
∴.
又∵四边形PEMF是矩形,
∴矩形PEMF是正方形,
即当点P运动到BC的中点时,四边形PEMF是正方形.
21.(1)四边形是正方形,是平行四边形,
,,,
在和中,
,
,
;
(2)由题意可知:,
,
,
,,
由(1)得.
22.(1)证明:∵四边形ABCD是正方形,
∴,
∵,
∴.
∴,
即.
∵,
∴.
(2)证明:如下图:
∵,,
∴·
∴,
∵,
∴,
∴,
∴.
(3)解:如图,过点B作交AE的延长线于点F.
∵,,
∴由勾股定理得:.
由(2)知,,
∴由勾股定理得:,
∵,
∴,
∵,
∴,
∴,
由勾股定理得:,
∴,
∴.
∴,
在中,由勾股定理得:,
.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
