冀教版数学八年级上册 13.2全等三角形教案(表格式)
文档属性
| 名称 | 冀教版数学八年级上册 13.2全等三角形教案(表格式) |

|
|
| 格式 | doc | ||
| 文件大小 | 246.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-15 00:00:00 | ||
图片预览


文档简介
全等三角形教学设计
教学目标 1.知道什么是全等形、全等三角形及全等三角形的对应元素;2.知道全吧能用符号正确地表示两个三角形全等;3.能熟练找出两个全等三角形的对应角、对应边.
教学重点 全等三角形的性质.
知识难点 找全等三角形的对应边、对应角
教学过程(师生活动) 设计理念
一、情景引入 多媒体演示:同一张底片洗出的照片,有什么特点呢? 通过实例创设情境,从“生活图片”过渡到“几何图形“,培养学生的观察能力,激发他们的学习兴趣.
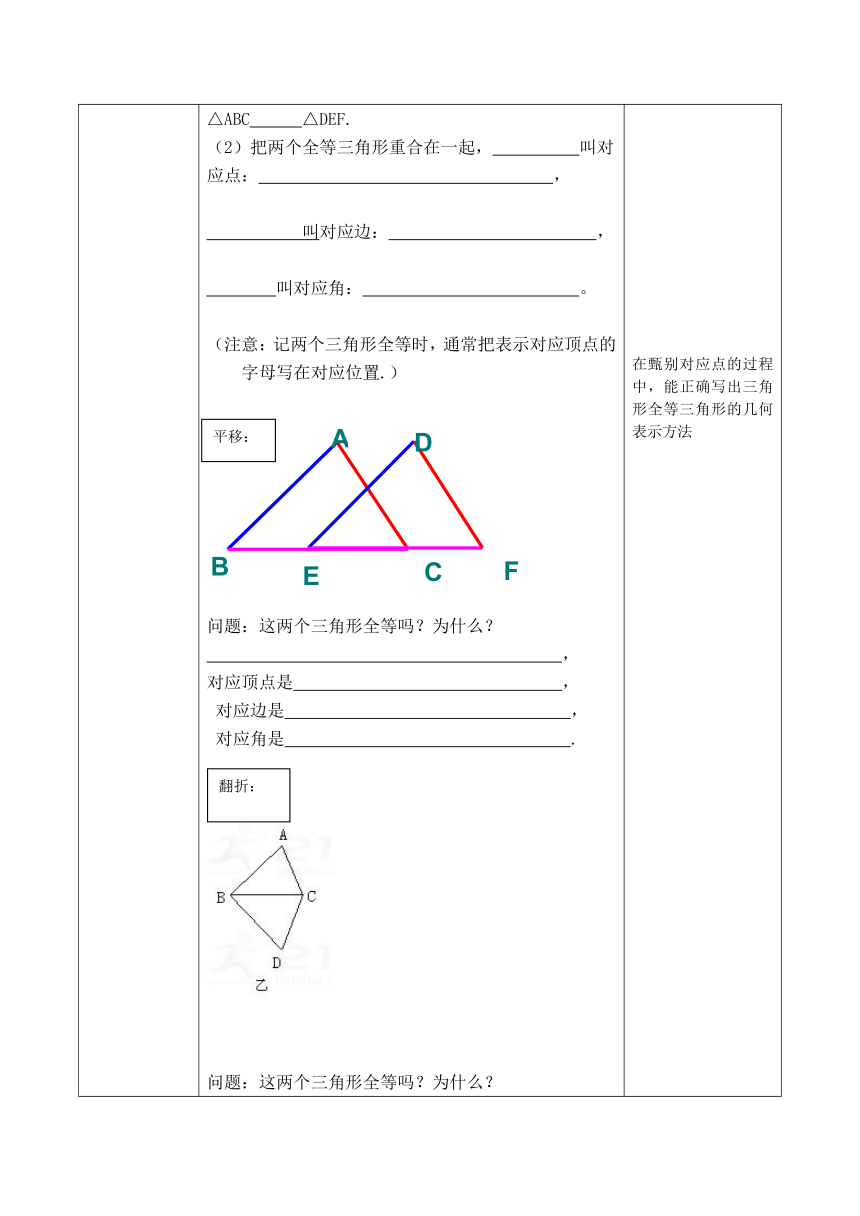
二、探究新知 1、全等形、全等三角形的有关概念 (1)观察图片思考:每组中的两个图形有什么特点?(形状 ,大小 .)(2)由此,你发现上述图形的共同特征是: 完全相同——放在一起能够 . (3)进而得出概念: 叫做全等形.类似的 叫做全等三角形. 2. 对应顶点,对应边和对应角 前后的两个三角形有什么关系?(1)△ABC与△DEF全等,记作△ABC △DEF,读作△ABC △DEF.(2)把两个全等三角形重合在一起, 叫对应点: , 叫对应边: , 叫对应角: 。(注意:记两个三角形全等时,通常把表示对应顶点的字母写在对应位置.) 问题:这两个三角形全等吗?为什么? ,对应顶点是 , 对应边是 , 对应角是 .问题:这两个三角形全等吗?为什么? ,对应顶点是 , 对应边是 , 对应角是 . 问题:这两个三角形全等吗?为什么? ,对应顶点是 , 对应边是 , 对应角是 .结论:一个图形经过平移、翻折、旋转后, 变化了,但 、 都没有改变,即平移、翻折、旋转前后的图形 。确定全等三角形的对应边、对应角还有哪些规律?3、全等三角形的性质 (1)全等三角形的性质.全等三角形的 相等;全等三角形的 相等(2)如图,△ABC与△DEF全等,请用数学符号表示出: , , 。例 如图,已知点A,D,B,F在同一条直线上, △ABC≌△FDE,AB=8 cm,BD=6 cm. 求FB的长. 引导学生仔细观察并归纳出全等形,全等三角形的定义及对应顶点,对应边,对应角在甄别对应点的过程中,能正确写出三角形全等三角形的几何表示方法 让学生充分发表意见,并通过观察、动脑思考能正确写出对应边,对应角。
三、自主练习 1、下列说法:①全等三角形的对应边相等,对应角相等;②全等三角形的周长相等,面积也相等;③面积相等的三角形是全等三角形;④周长相等的三角形是全等三角形,正确的说法是( ) A ②③ B ③④ C ①② D ①②③ 2、△ABC≌△DEF,∠A的对应角是∠D,∠B的对应角∠E,则∠C与_______是对应角;AB与_______是对应边,BC与_______是对应边,AC与_______是对应边.3、如图△ ABD ≌ △CDB,若AB=4,AD=5,BD=6,求BC、CD的长. 遵循学生的认知规律,有意识、有计划、有条理地设计一些问题,可让学生始终处在积极的思维状态,不知不觉中接受了新知识,分散了难点
四、归纳总结 1. 这节课在动手实际操作中,得到了全等三角形的哪些知识?全等三角形的概念、性质、表示方法、对应写法2. 找全等三角形对应元素的方法有哪些?A、大边对应大边,大角对应大角 B、公共边是对应边,公共角是对应角,对顶角也是对应角。 C、对应边所对的角是对应角,对应角所对的边是对应边 设计意图 :提升兴趣,复习总结。 时间分配: 2分钟
五、巩固提升 将本节课出错的题记录在纠错本上 进一步巩固所学知识,感受新知识的用途。
布置作业 必做题 教材第32页练习第1,2题.选做题 教材第33页习题12.1第3,4,5题. 加深学生对全等三角形的理解。
教学反思
在本节课中,我利用生活图片创设情境引入全等形及全等三角形的概念,学生当堂对全等三角形的理解较好,通过图形变换平移、翻折、旋转的过程加深全等三角形的对应顶点、对应边、对应角的理解,从中进一步引出全等三角形的性质。为了能突破难点,在设计上可先让学生拿着自己制作好的两个全等三角形进行平移、翻折与旋转,观察前后的变化,同时写出每次变换后的对应边、对应角,可同桌之间互相考察,也可一名学生指派另一名学生答题,然后老师再用几何画板进行动态演示,把实际操作逐步变为头脑中的印象,最后达到不用任何辅助手段就能在头脑中达到上述目的.
A
B
C
E
D
F
E
D
F
A
B
C
平移:
翻折:
旋转:
教学目标 1.知道什么是全等形、全等三角形及全等三角形的对应元素;2.知道全吧能用符号正确地表示两个三角形全等;3.能熟练找出两个全等三角形的对应角、对应边.
教学重点 全等三角形的性质.
知识难点 找全等三角形的对应边、对应角
教学过程(师生活动) 设计理念
一、情景引入 多媒体演示:同一张底片洗出的照片,有什么特点呢? 通过实例创设情境,从“生活图片”过渡到“几何图形“,培养学生的观察能力,激发他们的学习兴趣.
二、探究新知 1、全等形、全等三角形的有关概念 (1)观察图片思考:每组中的两个图形有什么特点?(形状 ,大小 .)(2)由此,你发现上述图形的共同特征是: 完全相同——放在一起能够 . (3)进而得出概念: 叫做全等形.类似的 叫做全等三角形. 2. 对应顶点,对应边和对应角 前后的两个三角形有什么关系?(1)△ABC与△DEF全等,记作△ABC △DEF,读作△ABC △DEF.(2)把两个全等三角形重合在一起, 叫对应点: , 叫对应边: , 叫对应角: 。(注意:记两个三角形全等时,通常把表示对应顶点的字母写在对应位置.) 问题:这两个三角形全等吗?为什么? ,对应顶点是 , 对应边是 , 对应角是 .问题:这两个三角形全等吗?为什么? ,对应顶点是 , 对应边是 , 对应角是 . 问题:这两个三角形全等吗?为什么? ,对应顶点是 , 对应边是 , 对应角是 .结论:一个图形经过平移、翻折、旋转后, 变化了,但 、 都没有改变,即平移、翻折、旋转前后的图形 。确定全等三角形的对应边、对应角还有哪些规律?3、全等三角形的性质 (1)全等三角形的性质.全等三角形的 相等;全等三角形的 相等(2)如图,△ABC与△DEF全等,请用数学符号表示出: , , 。例 如图,已知点A,D,B,F在同一条直线上, △ABC≌△FDE,AB=8 cm,BD=6 cm. 求FB的长. 引导学生仔细观察并归纳出全等形,全等三角形的定义及对应顶点,对应边,对应角在甄别对应点的过程中,能正确写出三角形全等三角形的几何表示方法 让学生充分发表意见,并通过观察、动脑思考能正确写出对应边,对应角。
三、自主练习 1、下列说法:①全等三角形的对应边相等,对应角相等;②全等三角形的周长相等,面积也相等;③面积相等的三角形是全等三角形;④周长相等的三角形是全等三角形,正确的说法是( ) A ②③ B ③④ C ①② D ①②③ 2、△ABC≌△DEF,∠A的对应角是∠D,∠B的对应角∠E,则∠C与_______是对应角;AB与_______是对应边,BC与_______是对应边,AC与_______是对应边.3、如图△ ABD ≌ △CDB,若AB=4,AD=5,BD=6,求BC、CD的长. 遵循学生的认知规律,有意识、有计划、有条理地设计一些问题,可让学生始终处在积极的思维状态,不知不觉中接受了新知识,分散了难点
四、归纳总结 1. 这节课在动手实际操作中,得到了全等三角形的哪些知识?全等三角形的概念、性质、表示方法、对应写法2. 找全等三角形对应元素的方法有哪些?A、大边对应大边,大角对应大角 B、公共边是对应边,公共角是对应角,对顶角也是对应角。 C、对应边所对的角是对应角,对应角所对的边是对应边 设计意图 :提升兴趣,复习总结。 时间分配: 2分钟
五、巩固提升 将本节课出错的题记录在纠错本上 进一步巩固所学知识,感受新知识的用途。
布置作业 必做题 教材第32页练习第1,2题.选做题 教材第33页习题12.1第3,4,5题. 加深学生对全等三角形的理解。
教学反思
在本节课中,我利用生活图片创设情境引入全等形及全等三角形的概念,学生当堂对全等三角形的理解较好,通过图形变换平移、翻折、旋转的过程加深全等三角形的对应顶点、对应边、对应角的理解,从中进一步引出全等三角形的性质。为了能突破难点,在设计上可先让学生拿着自己制作好的两个全等三角形进行平移、翻折与旋转,观察前后的变化,同时写出每次变换后的对应边、对应角,可同桌之间互相考察,也可一名学生指派另一名学生答题,然后老师再用几何画板进行动态演示,把实际操作逐步变为头脑中的印象,最后达到不用任何辅助手段就能在头脑中达到上述目的.
A
B
C
E
D
F
E
D
F
A
B
C
平移:
翻折:
旋转:
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
