青岛版数学八年级上册 1.3.2用尺规作三角形课件(共19张PPT)
文档属性
| 名称 | 青岛版数学八年级上册 1.3.2用尺规作三角形课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 679.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-16 00:00:00 | ||
图片预览




文档简介
(共19张PPT)
第1章 全等三角形
1.3 尺规作图
第2课时 用尺规作三角形
学习目标
1
通过合作探究理解三角形的基本作图原理,掌握三角形的基本作图方法.
2
能够根据要求熟练使用尺规进行三角形的实际作图.
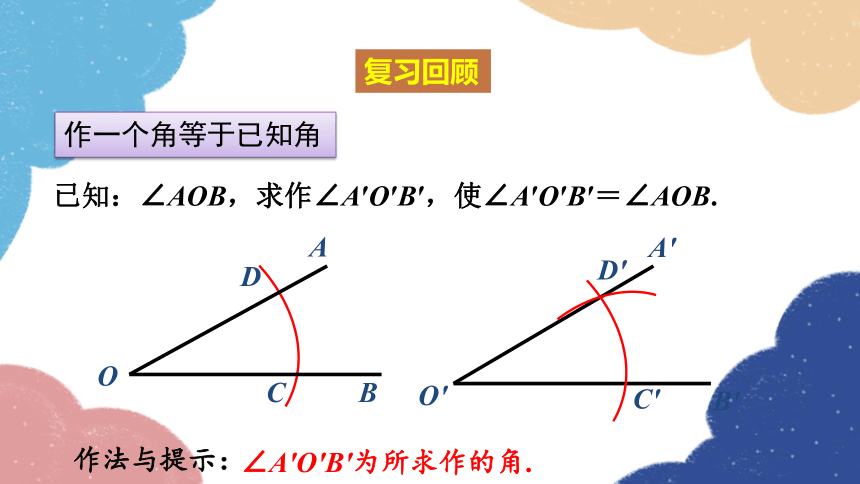
已知:∠AOB,求作∠A′O′B′,使∠A′O′B′=∠AOB.
O
B
A
C
D
O′
B′
A′
D′
C′
∠A′O′B′为所求作的角.
作法与提示:
复习回顾
作一个角等于已知角
豆豆书上的三角形被墨迹污染了一部分,他想在作业本上画出一个与书上完全一样的三角形,你能帮他画出来吗?
新知引入
已知三角形的两角及夹边,求作这个三角形
已知: ∠α , ∠β,线段c.
c
α
β
求作:△ABC,使∠A=∠α,∠B=∠β ,AB=c
α
β
A
B
C
c
假设这个三角形已作出.
合作探究
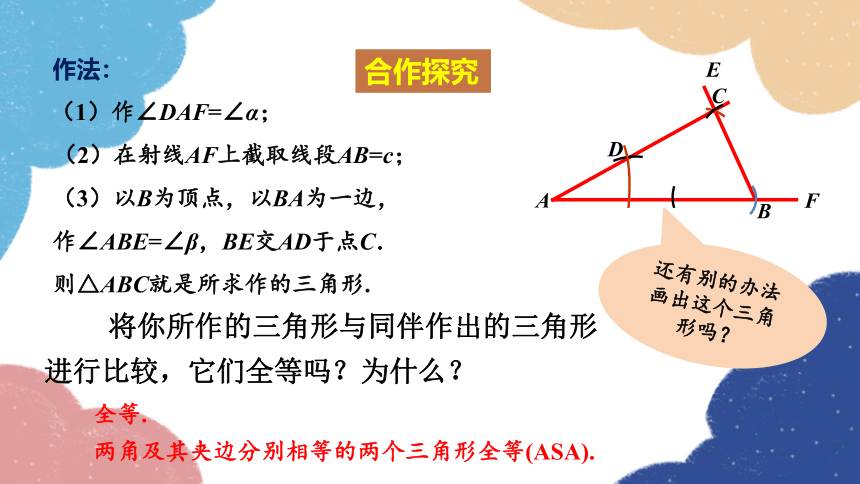
作法:
(1)作∠DAF=∠α;
(2)在射线AF上截取线段AB=c;
(3)以B为顶点,以BA为一边,作∠ABE=∠β,BE交AD于点C.
则△ABC就是所求作的三角形.
A
F
D
B
C
E
将你所作的三角形与同伴作出的三角形进行比较,它们全等吗?为什么?
全等.
两角及其夹边分别相等的两个三角形全等(ASA).
还有别的办法画出这个三角形吗?
合作探究
角
角
夹边
回顾刚才作三角形的顺序
对于边和角,也可以先作__,再作__,最后作__.
角
角
边
夹边
角
角
合作探究
B
A
F
D
C
E
作法2:
(1)作线段AB=c;
(2)以A为顶点,以AB为一边,作∠DAB=∠α;
(3)以B为顶点,以BA为一边,
作∠ABE=∠β,BE交AD于点C.
△ABC就是所求作的三角形.
D
A
B
C
E
合作探究
已知:线段a,c,∠α.
求作:△ABC,使BC=a , AB=c,∠ABC= ∠α.
a
c
α
B
A
C
α
a
c
假设这个三角形已作出.
合作探究
已知三角形的两边及夹角,求作这个三角形
作法:
(1)作一条线段BC=a;
(2)以B为顶点,以BC为一边作∠DBC= ∠α;
(3)在射线BD上截取线段BA=c;
A
B
C
D
将你所作的三角形与同伴作出的三角形进行比较,它们全等吗?为什么?
全等.
两边及其夹角分别相等的两个三角形全等(SAS).
还有别的办法画出这个三角形吗?
合作探究
回顾刚才作三角形的顺序
边
边
夹角
夹角
边
边
对于边和角,也可以先作__,再作__,最后作__.
边
角
边
合作探究
A
B
C
D
作法2:
(1)作∠DBE= ∠α;
(2)在射线BE上截取BC=a,在射线BD上截取BA=c;
(3)连接AC,即得所作三角形.
B
E
D
C
A
合作探究
已知三角形三条边,求作这个三角形
已知:线段 a,b,c.
求作: △ ABC,使AB=c,AC=b,BC=a.
合作探究
B
A
C
b
a
c
假设这个三角形已作出.
a
b
c
作法:
(1)作一条线段BC=a;
(2)分别以B,C为圆心,
以c,b为半径画弧,两弧交于A点;
(3)连接AB,AC,△ABC就是所求作的三角形.
B
C
A
将你所作的三角形与同伴作出的三角形进行比较,它们全等吗?为什么?
全等.
三边分别相等的两个三角形全等(SSS).
合作探究
经过前面的实践,我们如何来分析作图题呢?
1.假设所求作的图形已经作出,并在草稿纸上作出草图;
2.在草图上标出已给的边、角的对应位置;
3.从草图中首先找出基本图形,由此确定作图的起始步骤;
4.在3的基础上逐步向所求图形扩展.
归纳小结
1.利用尺规不能唯一作出的三角形是( )
A.已知三边 B.已知两边及夹角
C.已知两角及夹边 D.已知两边及其中一边的对角
2.利用尺规不可作的直角三角形是( )
A.已知斜边及一条直角边 B.已知两条直角边
C.已知两锐角 D.已知一锐角及一直角边
D
C
当堂检测
a
b
3.已知:直角,线段a,b.
求作:直角三角形ABC,使BC=a,AC=b.
当堂检测
C
D
E
B
A
作法:
(1)作∠DCE=90°;
(2)在射线CD、CE上分别截取CB=a,CA=b ;
(3)连接AB.
△ABC就是所求作的三角形.
1.用尺规作三角形,需要给出有关三角形的3个条件.
2.给出三角形的两边及其夹角、两角及其夹边、三条边,都可以画出唯一的三角形.
3.当已知两边及夹角时可以确定一个三角形,因此可以用来判定两个三角形全等;当已知两边及一边的对角时,会画出两个不同的三角形,因此不能用来作为判定两个三角形全等的条件.
归纳总结
用尺规作三角形
你知道的常用作图语言有哪些呢?
(1)作∠......=∠...... ;
(2)在......上截取,使......= ...... ;
(3)以......为顶点,以......为一边,作∠...... =∠ ...... ;
(4)作一条线段...... = ...... ;
(5)连接...... ,或连接......交......于点...... ;
(6)分别以......, ......为圆心,以......, ......为半径画弧, 两弧交于......点;
......
归纳总结
第1章 全等三角形
1.3 尺规作图
第2课时 用尺规作三角形
学习目标
1
通过合作探究理解三角形的基本作图原理,掌握三角形的基本作图方法.
2
能够根据要求熟练使用尺规进行三角形的实际作图.
已知:∠AOB,求作∠A′O′B′,使∠A′O′B′=∠AOB.
O
B
A
C
D
O′
B′
A′
D′
C′
∠A′O′B′为所求作的角.
作法与提示:
复习回顾
作一个角等于已知角
豆豆书上的三角形被墨迹污染了一部分,他想在作业本上画出一个与书上完全一样的三角形,你能帮他画出来吗?
新知引入
已知三角形的两角及夹边,求作这个三角形
已知: ∠α , ∠β,线段c.
c
α
β
求作:△ABC,使∠A=∠α,∠B=∠β ,AB=c
α
β
A
B
C
c
假设这个三角形已作出.
合作探究
作法:
(1)作∠DAF=∠α;
(2)在射线AF上截取线段AB=c;
(3)以B为顶点,以BA为一边,作∠ABE=∠β,BE交AD于点C.
则△ABC就是所求作的三角形.
A
F
D
B
C
E
将你所作的三角形与同伴作出的三角形进行比较,它们全等吗?为什么?
全等.
两角及其夹边分别相等的两个三角形全等(ASA).
还有别的办法画出这个三角形吗?
合作探究
角
角
夹边
回顾刚才作三角形的顺序
对于边和角,也可以先作__,再作__,最后作__.
角
角
边
夹边
角
角
合作探究
B
A
F
D
C
E
作法2:
(1)作线段AB=c;
(2)以A为顶点,以AB为一边,作∠DAB=∠α;
(3)以B为顶点,以BA为一边,
作∠ABE=∠β,BE交AD于点C.
△ABC就是所求作的三角形.
D
A
B
C
E
合作探究
已知:线段a,c,∠α.
求作:△ABC,使BC=a , AB=c,∠ABC= ∠α.
a
c
α
B
A
C
α
a
c
假设这个三角形已作出.
合作探究
已知三角形的两边及夹角,求作这个三角形
作法:
(1)作一条线段BC=a;
(2)以B为顶点,以BC为一边作∠DBC= ∠α;
(3)在射线BD上截取线段BA=c;
A
B
C
D
将你所作的三角形与同伴作出的三角形进行比较,它们全等吗?为什么?
全等.
两边及其夹角分别相等的两个三角形全等(SAS).
还有别的办法画出这个三角形吗?
合作探究
回顾刚才作三角形的顺序
边
边
夹角
夹角
边
边
对于边和角,也可以先作__,再作__,最后作__.
边
角
边
合作探究
A
B
C
D
作法2:
(1)作∠DBE= ∠α;
(2)在射线BE上截取BC=a,在射线BD上截取BA=c;
(3)连接AC,即得所作三角形.
B
E
D
C
A
合作探究
已知三角形三条边,求作这个三角形
已知:线段 a,b,c.
求作: △ ABC,使AB=c,AC=b,BC=a.
合作探究
B
A
C
b
a
c
假设这个三角形已作出.
a
b
c
作法:
(1)作一条线段BC=a;
(2)分别以B,C为圆心,
以c,b为半径画弧,两弧交于A点;
(3)连接AB,AC,△ABC就是所求作的三角形.
B
C
A
将你所作的三角形与同伴作出的三角形进行比较,它们全等吗?为什么?
全等.
三边分别相等的两个三角形全等(SSS).
合作探究
经过前面的实践,我们如何来分析作图题呢?
1.假设所求作的图形已经作出,并在草稿纸上作出草图;
2.在草图上标出已给的边、角的对应位置;
3.从草图中首先找出基本图形,由此确定作图的起始步骤;
4.在3的基础上逐步向所求图形扩展.
归纳小结
1.利用尺规不能唯一作出的三角形是( )
A.已知三边 B.已知两边及夹角
C.已知两角及夹边 D.已知两边及其中一边的对角
2.利用尺规不可作的直角三角形是( )
A.已知斜边及一条直角边 B.已知两条直角边
C.已知两锐角 D.已知一锐角及一直角边
D
C
当堂检测
a
b
3.已知:直角,线段a,b.
求作:直角三角形ABC,使BC=a,AC=b.
当堂检测
C
D
E
B
A
作法:
(1)作∠DCE=90°;
(2)在射线CD、CE上分别截取CB=a,CA=b ;
(3)连接AB.
△ABC就是所求作的三角形.
1.用尺规作三角形,需要给出有关三角形的3个条件.
2.给出三角形的两边及其夹角、两角及其夹边、三条边,都可以画出唯一的三角形.
3.当已知两边及夹角时可以确定一个三角形,因此可以用来判定两个三角形全等;当已知两边及一边的对角时,会画出两个不同的三角形,因此不能用来作为判定两个三角形全等的条件.
归纳总结
用尺规作三角形
你知道的常用作图语言有哪些呢?
(1)作∠......=∠...... ;
(2)在......上截取,使......= ...... ;
(3)以......为顶点,以......为一边,作∠...... =∠ ...... ;
(4)作一条线段...... = ...... ;
(5)连接...... ,或连接......交......于点...... ;
(6)分别以......, ......为圆心,以......, ......为半径画弧, 两弧交于......点;
......
归纳总结
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
